人教版高中数学选择性必修第一册第一章 空间向量与立体几何 章节综合训练(含解析)
文档属性
| 名称 | 人教版高中数学选择性必修第一册第一章 空间向量与立体几何 章节综合训练(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-02 21:50:56 | ||
图片预览




文档简介
人教版高中数学选择性必修第一册
第一章空间向量与立体几何章节综合训练
(120分钟 150分)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知向量a=(1,,2),b=(2,-1,k),且a与b互相垂直,则k的值是( )
A.-1 B. C.1 D.-
2.若a,b,c是空间任意三个向量,λ∈R,下列关系中,不成立的是( )
A.a+b=b+a B.λ(a+b)=λa+λb
C.(a+b)+c=a+(b+c) D.b=λa
3如图,空间四边形ABCD中,E,F分别是BC,CD的中点,则++等于( )
A. B. C. D.
4.若A(1,-2,1),B(4,2,3),C(6,-1,4),则△ABC的形状是( )
A.不等边锐角三角形 B.直角三角形
C.钝角三角形 D.等边三角形
5.已知平面α的一个法向量为n1=(-1,-2,-1),平面β的一个法向量n2=(2,4,2),则不重合的平面α与平面β( )
A.平行 B.垂直
C.相交但不垂直 D.不确定
6.若a=e1+e2+e3,b=e1+e2-e3,c=e1-e2+e3,d=e1+2e2+3e3,d=αa+βb+γc,则α,β,γ分别为( )
A.,-1,- B.,1,
C.-,1,- D.,1,-
7.(2013·吉安高二检测)已知直线l1的方向向量a=(2,4,x),直线l2的方向向量b=(2,y,2),若|a|=6,且a⊥b,则x+y的值是( )
A.1或-3 B.-1或3
C.-3 D.1
8.已知A(1,-1,2),B(2,3,-1),C(-1,0,0),则△ABC的面积是( )
A. B. C. D.
9.下列命题正确的是( )
A.若=+,则P,A,B三点共线
B.若{a,b,c}是空间的一个基底,则{a+b,b+c,a+c}构成空间的另一个基底
C.(a·b)·c=|a|·|b|·|c|
D.△ABC为直角三角形的充要条件是·=0
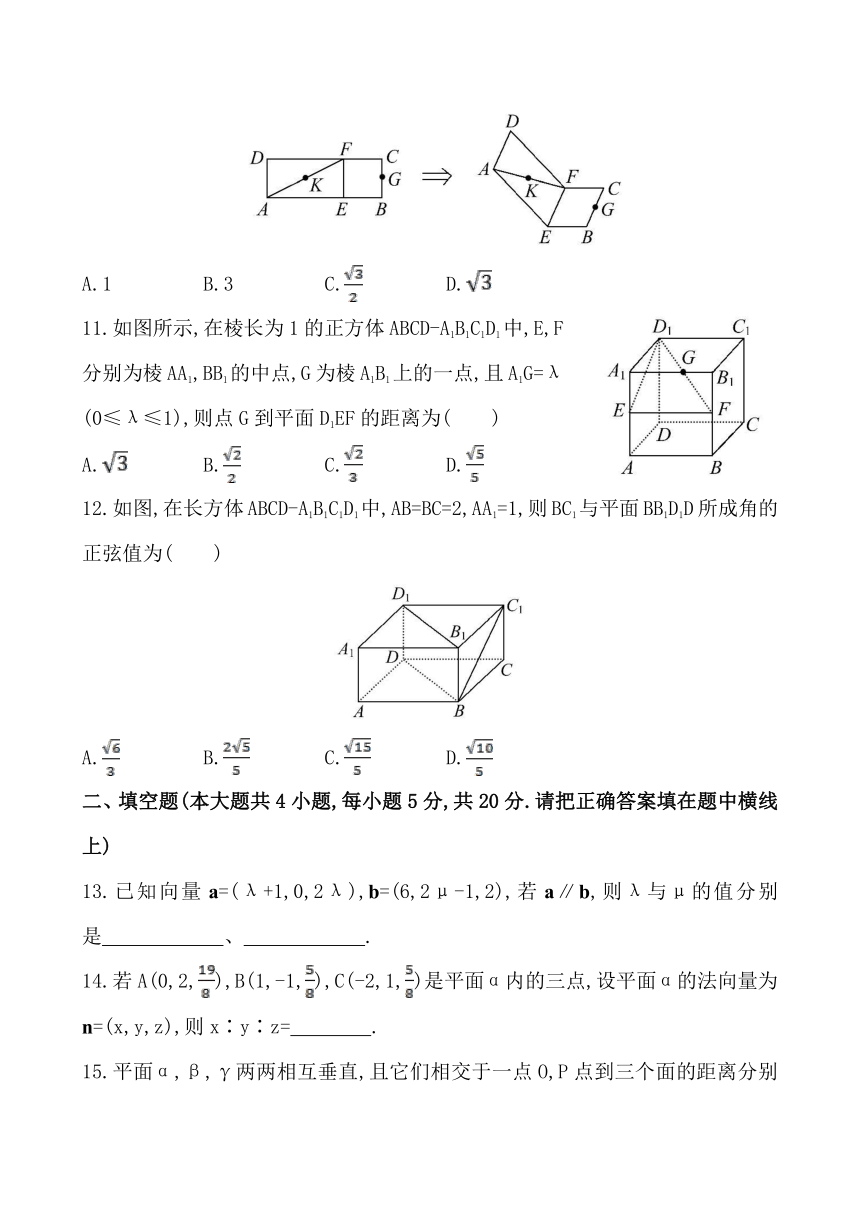
10.如图所示,四边形ABCD为矩形,AB=3,BC=1,EF∥BC且AE=2EB,G为BC的中点,K为△ADF的外心.沿EF将矩形折成一个120°的二面角A-EF-B,则此时KG的长是
( )
A.1 B.3 C. D.
11.如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别为棱AA1,BB1的中点,G为棱A1B1上的一点,且A1G=λ(0≤λ≤1),则点G到平面D1EF的距离为( )
A. B. C. D.
12.如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,则BC1与平面BB1D1D所成角的正弦值为( )
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)
13.已知向量a=(λ+1,0,2λ),b=(6,2μ-1,2),若a∥b,则λ与μ的值分别是 、 .
14.若A(0,2,),B(1,-1,),C(-2,1,)是平面α内的三点,设平面α的法向量为n=(x,y,z),则x∶y∶z= .
15.平面α,β,γ两两相互垂直,且它们相交于一点O,P点到三个面的距离分别是1cm,2 cm,3cm,则PO的长为 cm.
16.如图,平面PAD⊥平面ABCD,四边形ABCD为正方形,∠PAD=90°,且PA=AD=2,E,F分别是线段PA,CD的中点,则异面直线EF与BD所成角的余弦值为 .
三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)
17.(10分)已知空间三点A(0,2,3),B(-2,1,6),
C(1,-1,5),
(1)求以向量,为一组邻边的平行四边形的面积S.
(2)若向量a分别与向量,垂直,且|a|=,求向量a的坐标.
18.(12分)如图所示,在直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,∠ACB=
90°,侧棱AA1=2,CA=2,D是CC1的中点,试问在线段A1B上是否存在一点E(不与端点重合)使得点A1到平面AED的距离为
19.(12分)在长方体ABCD-A1B1C1D1中,AA1=AD=1,E为CD的中点.
(1)求证:B1E⊥AD1.
(2)在棱AA1上是否存在一点P,使得DP∥平面B1AE 若存在,求AP的长;若不存在,说明理由.
20.(12分)如图所示,在棱长为1的正方体ABCD-A'B'C'D'中,E,F分别是D'D,DB的中点,G在棱CD上,CG=CD,H为C'G的中点.
(1)求证:EF⊥B'C.
(2)求EF,C'G所成角的余弦值.
(3)求FH的长.
21.(12分)如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=PA.点O,D分别是AC,PC的中点,OP⊥底面ABC.
(1)求证:OD∥平面PAB.
(2)求直线OD与平面PBC所成角的正弦值.
22.(12分)(能力挑战题)已知四棱锥P-ABCD中,PA⊥
平面ABCD,且PA=4PQ=4,底面为直角梯形,∠CDA=
∠BAD=90°,AB=2,CD=1,AD=,M,N分别是PD,PB
的中点.
(1)求证:MQ∥平面PCB.
(2)求截面MCN与底面ABCD所成二面角的大小.
(3)求点A到平面MCN的距离.
答案解析
1.【解析】选D.a·b=2-+2k=0,∴k=-.
2.【解析】选D.由向量的运算律知,A,B,C均正确,对于D,当a=0,b≠0时,不成立.
3.【解析】选C.++=++=.
4.【解析】选A.=(3,4,2),=(5,1,3),
=(2,-3,1).由·>0,得A为锐角;
由·>0,得C为锐角;
由·>0,得B为锐角,且||≠||≠||,
所以△ABC为不等边锐角三角形.
5.【解析】选A.∵n2=-2n1,∴n2∥n1,故α∥β.
6.【解析】选A.由d=αa+βb+γc
=α(e1+e2+e3)+β(e1+e2-e3)+γ(e1-e2+e3)
=(α+β+γ)e1+(α+β-γ)e2+(α-β+γ)e3=e1+2e2+3e3.∴解得α=,β=-1,γ=-.
7.【解析】选A.根据|a|=6,可得x=±4,当x=4时,y=-3,当x=-4时,y=1,所以x+y=1或-3.
8.【解析】选C.易知=(1,4,-3),=(-2,1,-2),∴||=,||=3,
cos<,>==,∴sin<,>==,
∴S△ABC=||·||sin<,>=.
9.【解析】选B.P,A,B三点共面不一定共线,故A错误;由数量积公式知C错误;△ABC为直角三角形时可能·=0,也可能·=0,或·=0,故D错误.
10.【解析】选D.由题意知K为AF的中点,取EF的中点H,连接KH,GH易证明
∠KHG即为二面角A-EF-B的平面角,在△KHG中,由KH=HG=1,∠KHG=120°,可解得KG=.
11.【解题指南】可以根据几何的有关性质转化为点A1到直线D1E的距离,利用三角形的面积可求;或建立空间直角坐标系,利用平面的法向量来求.
【解析】选D.方法一:∵A1B1∥EF,G在A1B1上,
∴G到平面D1EF的距离即为A1到平面D1EF的距离,也就是A1到D1E的距离.
∵D1E=,
∴由三角形面积可得h==.
方法二:以的方向作为x轴,y轴,z轴的正方向建立空间直角坐标系,则E(0,0,),F(1,0,),D1(0,1,1),G(λ,0,1),
∴=(1,0,0),=(0,1,),=(-λ,1,0),
设平面EFD1的一个法向量是n=(x,y,z),则解得取y=1,则n=(0,1,-2).
∴点G到平面EFD1的距离是:h===.
12.【解析】选D.如图建立空间直角坐标系,则B(2,2,0),D1(0,0,1),C1(0,2,1),
∴=(0,0,1),=(2,2,0),=(-2,0,1).
设平面BB1D1D的一个法向量n=(x,y,z),
由可得
∴可取n=(1,-1,0).
cos= ==,
∴BC1与平面BB1D1D所成角的正弦值为.
13.【解析】∵a∥b,∴存在实数k,使得a=kb,
即(λ+1,0,2λ)=k(6,2μ-1,2),
∴解得k=λ=,μ=.
答案:
14.【解析】=(1,-3,-),=(-2,-1,-),
∵∴
∴x∶y∶z=y∶y∶(-y)=2∶3∶(-4).
答案:2∶3∶(-4)
15.【解析】如图所示,建立空间直角坐标系,不妨设O(0,0,0),P(1,2,3),
∴|OP|==(cm).
答案:
16.【解析】∵=-,=-++=-++,∴·= (-)·(-++)=4-2=2.
||2=(-++)2=6,∴||=,||=2,∴cos<,>= ==,
即异面直线EF与BD所成角的余弦值为.
答案:
【一题多解】如图所示,建立空间直角坐标系Axyz,
∴E(0,0,1),F(1,2,0),B(2,0,0),D(0,2,0),
∴=(1,2,-1),=(-2,2,0),
∴cos<,>==,
∴异面直线EF与BD所成角的余弦值为.
17.【解析】(1)∵=(-2,-1,3),=(1,-3,2),
∴cos∠BAC==,
∴∠BAC=60°,∴S=||||sin 60°=7.
(2)设a=(x,y,z),则a⊥ -2x-y+3z=0,
a⊥ x-3y+2z=0,|a|= x2+y2+z2=3,
解得x=y=z=1或x=y=z=-1,
∴a=(1,1,1),或a=(-1,-1,-1).
18.【解析】存在.以CA,CB,CC1所在的直线为x轴,y轴和z轴,建立如图所示的空间直角坐标系,
则A(2,0,0),A1(2,0,2),
D(0,0,1),B(0,2,0),
设=λ,λ∈(0,1),
则E(2λ,2(1-λ),2λ).
又=(-2,0,1),
=(2(λ-1),2(1-λ),2λ),
设n=(x,y,z)为平面AED的法向量,
则即
取x=1,则y=,z=2,即n=(1,,2).
由于d==,
∴=,又λ∈(0,1),解得λ=,
∴当点E为A1B的中点时,A1到平面AED的距离为.
【拓展提升】探索性问题的解法
在立体几何中,经常会遇到点、线、面处在什么位置时结论成立,或某一结论成立时需要具备什么条件,或某一结论在某一条件下,某个元素在某个位置时是否成立等类似的问题.这些问题都属探索性问题,解决这些问题仅凭几何手段有时会十分困难,我们借助向量将“形”转化为“数”,把点、线、面的位置数量化,通过对代数式的运算就可得出相应的结论.这样可以使许多几何问题进行类化,公式化,使问题的解决变得有“法”可依,有路可寻.
19.【解析】以A为原点,,,的方向分别为x轴、y轴、z轴的正方向建立空间直角坐标系.
设AB=a,则A(0,0,0),D(0,1,0),D1(0,1,1),
E(,1,0),B1(a,0,1),
(1)=(0,1,1),=(-,1,-1),
∵·=-×0+1×1+(-1)×1=0,
∴B1E⊥AD1.
(2)假设在棱AA1上存在一点P(0,0,z0),使得DP∥平面B1AE,此时=(0,-1,z0),又设平面B1AE的法向量为n=(x,y,z).
∵n⊥平面B1AE,=(a,0,1),=(,1,0),
∴n⊥,n⊥,得
取x=1,得平面B1AE的一个法向量n=(1,-,-a),要使DP∥平面B1AE,
只需n⊥,有-az0=0,解得:z0=.
∴AP=,∴在棱AA1上存在点P,使得DP∥平面B1AE,且P为AA1的中点.
20.【解题指南】要证明EF⊥B'C,只需要证明·=0;要求EF,C'G所成角的余弦值,只要求出,所成角的余弦值;要求FH的长,只要求出|即可.
【解析】(1)设=a,=b,=c,
则c·b=b·a=c·a=0,|a|2=a2=1,|b|2=b2=1,|c|2=c2=1.
∵=+=-c+(a-b)
=(a-b-c),
=-=b-c,
∴·=(a-b-c)·(b-c)=(c2-b2)
=×(1-1)=0.∴EF⊥B'C.
(2)∵=(a-b-c),=+=-c-a,
∴·=(a-b-c)·(-c-a)
=(-a2+c2)=,
||2=(a-b-c)2=(a2+b2+c2)=,
||2=(-c-a)2=c2+a2=,
∴||=,||=,
cos<,>==,
∴EF,C'G所成角的余弦值为.
(3)∵=+++=(a-b)+b+c+=(a-b)+b+c+(-c-a)=a+b+c,
∴||2=(a+b+c)2
=a2+b2+c2=,
∴FH的长为.
21.【解析】方法一:(1)∵O,D分别为AC,PC的中点,∴OD∥PA.
又PA 平面PAB,
OD 平面PAB,
∴OD∥平面PAB.
(2)设PA=2a,∵AB⊥BC,OA=OC,
∴OA=OB=OC=a.
又∵OP⊥平面ABC,∴PA=PB=PC=2a.
取BC中点E,连接PE,则BC⊥平面POE.
作OF⊥PE于F,连接DF,则OF⊥平面PBC.
∴∠ODF是OD与平面PBC所成的角.
∵PA=2a,OA=a,∴OP=a.
又∵OE=,∴OF=a.
在Rt△ODF中,sin∠ODF==,
∴OD与平面PBC所成角的正弦值为.
方法二:∵OP⊥平面ABC,OA=OC,AB=BC,
∴OA⊥OB,OA⊥OP,OB⊥OP.
以O为原点,建立空间直角坐标系Oxyz(如图),
设AB=a,则A(a,0,0),
B(0,a,0),C(-a,0,0).
设OP=h,则P(0,0,h).
(1)∵D为PC的中点,
∴=(-a,0,h).
又=(a,0,-h),∴=-.
∴∥,又PA 平面PAB,OD 平面PAB,
∴OD∥平面PAB.
(2)∵PA=2a,∴h=a,
∴=(-a,0,a).
可求得平面PBC的一个法向量n=(-1,1,),
∴cos<,n>==.
设OD与平面PBC所成的角为θ,
则sinθ=|cos<,n>|=.
∴OD与平面PBC所成角的正弦值为.
22.【解析】方法一:以A为原点,以AD,AB,AP所在直线分别为x轴,y轴,z轴建立空间直角坐标系Axyz,由AB=2,CD=1,AD=,PA=4PQ=4,M,N分别是PD,PB的中点,可得A(0,0,0),
B(0,2,0),C(,1,0),
D(,0,0),P(0,0,4),Q(0,0,3),M(,0,2),N(0,1,2).
(1)=(,-1,0),=(0,2,-4),=(-,0,1).设平面PBC的法向量为n0=(x,y,z),
则有:n0⊥ (x,y,z)·(,-1,0)=0 x-y=0,n0⊥ (x,y,z)·(0,2,-4)=
0 2y-4z=0,
令z=1,则x=,y=2 n0=(,2,1).
∴·n0=(-,0,1)·(,2,1)=0,
又MQ 平面PCB,∴MQ∥平面PCB.
(2)设平面的MCN的法向量为n=(x',y',z'),
又=(-,-1,2),=(-,0,2),
则有:
n⊥ (x',y',z')·(-,-1,2)=0 -x'-y'+2z'=0,
n⊥ (x',y',z')·(-,0,2)=0 -x'+2z'=0,
令z'=1,则x'=,y'=1 n=(,1,1).
又=(0,0,4)为平面ABCD的一个法向量.
∴cos= ==,
又截面MCN与底面ABCD所成二面角为锐二面角,
∴截面MCN与底面ABCD所成二面角的大小为.
(3)∵=(-,-1,0),∴所求的距离d===.
方法二:(1)取AP的中点E,连接ED,则ED∥CN,
依题有Q为EP的中点,所以MQ∥ED,所以MQ∥CN,又MQ 平面PCB,CN 平面PCB,∴MQ∥平面PCB.
(2)易证:平面MEN∥底面ABCD,
所以截面MCN与平面MEN所成的二面角即为平面MCN与底面ABCD所成的角,
因为PA⊥平面ABCD,所以PA⊥平面MEN,
过E作EF⊥MN,垂足为F,连接QF,则由三垂线定理可知QF⊥MN,
由(1)可知M,C,N,Q四点共面,
所以∠QFE为截面MCN与平面MEN所成的二面角的平面角.
在Rt△MEN中,ME=,NE=1,MN=,
故EF=,所以:tan∠QFE=,∠QFE=.
即所求二面角大小为.
(3)因为EP的中点为Q,且平面MCN与PA交于点Q,所以点A到平面MCN的距离是点E到平面MCN的距离的3倍,
由(2)知:MN⊥平面QEF,则平面MCNQ⊥平面QEF且交线为QF,
作EH⊥QF,垂足为H,则EH⊥平面MCNQ,故EH即为点E到平面MCN的距离.
在Rt△EQF中,EF=,∠QFE=,故EH=,即原点A到平面MCN的距离是.
PAGE
第一章空间向量与立体几何章节综合训练
(120分钟 150分)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知向量a=(1,,2),b=(2,-1,k),且a与b互相垂直,则k的值是( )
A.-1 B. C.1 D.-
2.若a,b,c是空间任意三个向量,λ∈R,下列关系中,不成立的是( )
A.a+b=b+a B.λ(a+b)=λa+λb
C.(a+b)+c=a+(b+c) D.b=λa
3如图,空间四边形ABCD中,E,F分别是BC,CD的中点,则++等于( )
A. B. C. D.
4.若A(1,-2,1),B(4,2,3),C(6,-1,4),则△ABC的形状是( )
A.不等边锐角三角形 B.直角三角形
C.钝角三角形 D.等边三角形
5.已知平面α的一个法向量为n1=(-1,-2,-1),平面β的一个法向量n2=(2,4,2),则不重合的平面α与平面β( )
A.平行 B.垂直
C.相交但不垂直 D.不确定
6.若a=e1+e2+e3,b=e1+e2-e3,c=e1-e2+e3,d=e1+2e2+3e3,d=αa+βb+γc,则α,β,γ分别为( )
A.,-1,- B.,1,
C.-,1,- D.,1,-
7.(2013·吉安高二检测)已知直线l1的方向向量a=(2,4,x),直线l2的方向向量b=(2,y,2),若|a|=6,且a⊥b,则x+y的值是( )
A.1或-3 B.-1或3
C.-3 D.1
8.已知A(1,-1,2),B(2,3,-1),C(-1,0,0),则△ABC的面积是( )
A. B. C. D.
9.下列命题正确的是( )
A.若=+,则P,A,B三点共线
B.若{a,b,c}是空间的一个基底,则{a+b,b+c,a+c}构成空间的另一个基底
C.(a·b)·c=|a|·|b|·|c|
D.△ABC为直角三角形的充要条件是·=0
10.如图所示,四边形ABCD为矩形,AB=3,BC=1,EF∥BC且AE=2EB,G为BC的中点,K为△ADF的外心.沿EF将矩形折成一个120°的二面角A-EF-B,则此时KG的长是
( )
A.1 B.3 C. D.
11.如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,E,F分别为棱AA1,BB1的中点,G为棱A1B1上的一点,且A1G=λ(0≤λ≤1),则点G到平面D1EF的距离为( )
A. B. C. D.
12.如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,则BC1与平面BB1D1D所成角的正弦值为( )
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)
13.已知向量a=(λ+1,0,2λ),b=(6,2μ-1,2),若a∥b,则λ与μ的值分别是 、 .
14.若A(0,2,),B(1,-1,),C(-2,1,)是平面α内的三点,设平面α的法向量为n=(x,y,z),则x∶y∶z= .
15.平面α,β,γ两两相互垂直,且它们相交于一点O,P点到三个面的距离分别是1cm,2 cm,3cm,则PO的长为 cm.
16.如图,平面PAD⊥平面ABCD,四边形ABCD为正方形,∠PAD=90°,且PA=AD=2,E,F分别是线段PA,CD的中点,则异面直线EF与BD所成角的余弦值为 .
三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)
17.(10分)已知空间三点A(0,2,3),B(-2,1,6),
C(1,-1,5),
(1)求以向量,为一组邻边的平行四边形的面积S.
(2)若向量a分别与向量,垂直,且|a|=,求向量a的坐标.
18.(12分)如图所示,在直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,∠ACB=
90°,侧棱AA1=2,CA=2,D是CC1的中点,试问在线段A1B上是否存在一点E(不与端点重合)使得点A1到平面AED的距离为
19.(12分)在长方体ABCD-A1B1C1D1中,AA1=AD=1,E为CD的中点.
(1)求证:B1E⊥AD1.
(2)在棱AA1上是否存在一点P,使得DP∥平面B1AE 若存在,求AP的长;若不存在,说明理由.
20.(12分)如图所示,在棱长为1的正方体ABCD-A'B'C'D'中,E,F分别是D'D,DB的中点,G在棱CD上,CG=CD,H为C'G的中点.
(1)求证:EF⊥B'C.
(2)求EF,C'G所成角的余弦值.
(3)求FH的长.
21.(12分)如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=PA.点O,D分别是AC,PC的中点,OP⊥底面ABC.
(1)求证:OD∥平面PAB.
(2)求直线OD与平面PBC所成角的正弦值.
22.(12分)(能力挑战题)已知四棱锥P-ABCD中,PA⊥
平面ABCD,且PA=4PQ=4,底面为直角梯形,∠CDA=
∠BAD=90°,AB=2,CD=1,AD=,M,N分别是PD,PB
的中点.
(1)求证:MQ∥平面PCB.
(2)求截面MCN与底面ABCD所成二面角的大小.
(3)求点A到平面MCN的距离.
答案解析
1.【解析】选D.a·b=2-+2k=0,∴k=-.
2.【解析】选D.由向量的运算律知,A,B,C均正确,对于D,当a=0,b≠0时,不成立.
3.【解析】选C.++=++=.
4.【解析】选A.=(3,4,2),=(5,1,3),
=(2,-3,1).由·>0,得A为锐角;
由·>0,得C为锐角;
由·>0,得B为锐角,且||≠||≠||,
所以△ABC为不等边锐角三角形.
5.【解析】选A.∵n2=-2n1,∴n2∥n1,故α∥β.
6.【解析】选A.由d=αa+βb+γc
=α(e1+e2+e3)+β(e1+e2-e3)+γ(e1-e2+e3)
=(α+β+γ)e1+(α+β-γ)e2+(α-β+γ)e3=e1+2e2+3e3.∴解得α=,β=-1,γ=-.
7.【解析】选A.根据|a|=6,可得x=±4,当x=4时,y=-3,当x=-4时,y=1,所以x+y=1或-3.
8.【解析】选C.易知=(1,4,-3),=(-2,1,-2),∴||=,||=3,
cos<,>==,∴sin<,>==,
∴S△ABC=||·||sin<,>=.
9.【解析】选B.P,A,B三点共面不一定共线,故A错误;由数量积公式知C错误;△ABC为直角三角形时可能·=0,也可能·=0,或·=0,故D错误.
10.【解析】选D.由题意知K为AF的中点,取EF的中点H,连接KH,GH易证明
∠KHG即为二面角A-EF-B的平面角,在△KHG中,由KH=HG=1,∠KHG=120°,可解得KG=.
11.【解题指南】可以根据几何的有关性质转化为点A1到直线D1E的距离,利用三角形的面积可求;或建立空间直角坐标系,利用平面的法向量来求.
【解析】选D.方法一:∵A1B1∥EF,G在A1B1上,
∴G到平面D1EF的距离即为A1到平面D1EF的距离,也就是A1到D1E的距离.
∵D1E=,
∴由三角形面积可得h==.
方法二:以的方向作为x轴,y轴,z轴的正方向建立空间直角坐标系,则E(0,0,),F(1,0,),D1(0,1,1),G(λ,0,1),
∴=(1,0,0),=(0,1,),=(-λ,1,0),
设平面EFD1的一个法向量是n=(x,y,z),则解得取y=1,则n=(0,1,-2).
∴点G到平面EFD1的距离是:h===.
12.【解析】选D.如图建立空间直角坐标系,则B(2,2,0),D1(0,0,1),C1(0,2,1),
∴=(0,0,1),=(2,2,0),=(-2,0,1).
设平面BB1D1D的一个法向量n=(x,y,z),
由可得
∴可取n=(1,-1,0).
cos
∴BC1与平面BB1D1D所成角的正弦值为.
13.【解析】∵a∥b,∴存在实数k,使得a=kb,
即(λ+1,0,2λ)=k(6,2μ-1,2),
∴解得k=λ=,μ=.
答案:
14.【解析】=(1,-3,-),=(-2,-1,-),
∵∴
∴x∶y∶z=y∶y∶(-y)=2∶3∶(-4).
答案:2∶3∶(-4)
15.【解析】如图所示,建立空间直角坐标系,不妨设O(0,0,0),P(1,2,3),
∴|OP|==(cm).
答案:
16.【解析】∵=-,=-++=-++,∴·= (-)·(-++)=4-2=2.
||2=(-++)2=6,∴||=,||=2,∴cos<,>= ==,
即异面直线EF与BD所成角的余弦值为.
答案:
【一题多解】如图所示,建立空间直角坐标系Axyz,
∴E(0,0,1),F(1,2,0),B(2,0,0),D(0,2,0),
∴=(1,2,-1),=(-2,2,0),
∴cos<,>==,
∴异面直线EF与BD所成角的余弦值为.
17.【解析】(1)∵=(-2,-1,3),=(1,-3,2),
∴cos∠BAC==,
∴∠BAC=60°,∴S=||||sin 60°=7.
(2)设a=(x,y,z),则a⊥ -2x-y+3z=0,
a⊥ x-3y+2z=0,|a|= x2+y2+z2=3,
解得x=y=z=1或x=y=z=-1,
∴a=(1,1,1),或a=(-1,-1,-1).
18.【解析】存在.以CA,CB,CC1所在的直线为x轴,y轴和z轴,建立如图所示的空间直角坐标系,
则A(2,0,0),A1(2,0,2),
D(0,0,1),B(0,2,0),
设=λ,λ∈(0,1),
则E(2λ,2(1-λ),2λ).
又=(-2,0,1),
=(2(λ-1),2(1-λ),2λ),
设n=(x,y,z)为平面AED的法向量,
则即
取x=1,则y=,z=2,即n=(1,,2).
由于d==,
∴=,又λ∈(0,1),解得λ=,
∴当点E为A1B的中点时,A1到平面AED的距离为.
【拓展提升】探索性问题的解法
在立体几何中,经常会遇到点、线、面处在什么位置时结论成立,或某一结论成立时需要具备什么条件,或某一结论在某一条件下,某个元素在某个位置时是否成立等类似的问题.这些问题都属探索性问题,解决这些问题仅凭几何手段有时会十分困难,我们借助向量将“形”转化为“数”,把点、线、面的位置数量化,通过对代数式的运算就可得出相应的结论.这样可以使许多几何问题进行类化,公式化,使问题的解决变得有“法”可依,有路可寻.
19.【解析】以A为原点,,,的方向分别为x轴、y轴、z轴的正方向建立空间直角坐标系.
设AB=a,则A(0,0,0),D(0,1,0),D1(0,1,1),
E(,1,0),B1(a,0,1),
(1)=(0,1,1),=(-,1,-1),
∵·=-×0+1×1+(-1)×1=0,
∴B1E⊥AD1.
(2)假设在棱AA1上存在一点P(0,0,z0),使得DP∥平面B1AE,此时=(0,-1,z0),又设平面B1AE的法向量为n=(x,y,z).
∵n⊥平面B1AE,=(a,0,1),=(,1,0),
∴n⊥,n⊥,得
取x=1,得平面B1AE的一个法向量n=(1,-,-a),要使DP∥平面B1AE,
只需n⊥,有-az0=0,解得:z0=.
∴AP=,∴在棱AA1上存在点P,使得DP∥平面B1AE,且P为AA1的中点.
20.【解题指南】要证明EF⊥B'C,只需要证明·=0;要求EF,C'G所成角的余弦值,只要求出,所成角的余弦值;要求FH的长,只要求出|即可.
【解析】(1)设=a,=b,=c,
则c·b=b·a=c·a=0,|a|2=a2=1,|b|2=b2=1,|c|2=c2=1.
∵=+=-c+(a-b)
=(a-b-c),
=-=b-c,
∴·=(a-b-c)·(b-c)=(c2-b2)
=×(1-1)=0.∴EF⊥B'C.
(2)∵=(a-b-c),=+=-c-a,
∴·=(a-b-c)·(-c-a)
=(-a2+c2)=,
||2=(a-b-c)2=(a2+b2+c2)=,
||2=(-c-a)2=c2+a2=,
∴||=,||=,
cos<,>==,
∴EF,C'G所成角的余弦值为.
(3)∵=+++=(a-b)+b+c+=(a-b)+b+c+(-c-a)=a+b+c,
∴||2=(a+b+c)2
=a2+b2+c2=,
∴FH的长为.
21.【解析】方法一:(1)∵O,D分别为AC,PC的中点,∴OD∥PA.
又PA 平面PAB,
OD 平面PAB,
∴OD∥平面PAB.
(2)设PA=2a,∵AB⊥BC,OA=OC,
∴OA=OB=OC=a.
又∵OP⊥平面ABC,∴PA=PB=PC=2a.
取BC中点E,连接PE,则BC⊥平面POE.
作OF⊥PE于F,连接DF,则OF⊥平面PBC.
∴∠ODF是OD与平面PBC所成的角.
∵PA=2a,OA=a,∴OP=a.
又∵OE=,∴OF=a.
在Rt△ODF中,sin∠ODF==,
∴OD与平面PBC所成角的正弦值为.
方法二:∵OP⊥平面ABC,OA=OC,AB=BC,
∴OA⊥OB,OA⊥OP,OB⊥OP.
以O为原点,建立空间直角坐标系Oxyz(如图),
设AB=a,则A(a,0,0),
B(0,a,0),C(-a,0,0).
设OP=h,则P(0,0,h).
(1)∵D为PC的中点,
∴=(-a,0,h).
又=(a,0,-h),∴=-.
∴∥,又PA 平面PAB,OD 平面PAB,
∴OD∥平面PAB.
(2)∵PA=2a,∴h=a,
∴=(-a,0,a).
可求得平面PBC的一个法向量n=(-1,1,),
∴cos<,n>==.
设OD与平面PBC所成的角为θ,
则sinθ=|cos<,n>|=.
∴OD与平面PBC所成角的正弦值为.
22.【解析】方法一:以A为原点,以AD,AB,AP所在直线分别为x轴,y轴,z轴建立空间直角坐标系Axyz,由AB=2,CD=1,AD=,PA=4PQ=4,M,N分别是PD,PB的中点,可得A(0,0,0),
B(0,2,0),C(,1,0),
D(,0,0),P(0,0,4),Q(0,0,3),M(,0,2),N(0,1,2).
(1)=(,-1,0),=(0,2,-4),=(-,0,1).设平面PBC的法向量为n0=(x,y,z),
则有:n0⊥ (x,y,z)·(,-1,0)=0 x-y=0,n0⊥ (x,y,z)·(0,2,-4)=
0 2y-4z=0,
令z=1,则x=,y=2 n0=(,2,1).
∴·n0=(-,0,1)·(,2,1)=0,
又MQ 平面PCB,∴MQ∥平面PCB.
(2)设平面的MCN的法向量为n=(x',y',z'),
又=(-,-1,2),=(-,0,2),
则有:
n⊥ (x',y',z')·(-,-1,2)=0 -x'-y'+2z'=0,
n⊥ (x',y',z')·(-,0,2)=0 -x'+2z'=0,
令z'=1,则x'=,y'=1 n=(,1,1).
又=(0,0,4)为平面ABCD的一个法向量.
∴cos
又截面MCN与底面ABCD所成二面角为锐二面角,
∴截面MCN与底面ABCD所成二面角的大小为.
(3)∵=(-,-1,0),∴所求的距离d===.
方法二:(1)取AP的中点E,连接ED,则ED∥CN,
依题有Q为EP的中点,所以MQ∥ED,所以MQ∥CN,又MQ 平面PCB,CN 平面PCB,∴MQ∥平面PCB.
(2)易证:平面MEN∥底面ABCD,
所以截面MCN与平面MEN所成的二面角即为平面MCN与底面ABCD所成的角,
因为PA⊥平面ABCD,所以PA⊥平面MEN,
过E作EF⊥MN,垂足为F,连接QF,则由三垂线定理可知QF⊥MN,
由(1)可知M,C,N,Q四点共面,
所以∠QFE为截面MCN与平面MEN所成的二面角的平面角.
在Rt△MEN中,ME=,NE=1,MN=,
故EF=,所以:tan∠QFE=,∠QFE=.
即所求二面角大小为.
(3)因为EP的中点为Q,且平面MCN与PA交于点Q,所以点A到平面MCN的距离是点E到平面MCN的距离的3倍,
由(2)知:MN⊥平面QEF,则平面MCNQ⊥平面QEF且交线为QF,
作EH⊥QF,垂足为H,则EH⊥平面MCNQ,故EH即为点E到平面MCN的距离.
在Rt△EQF中,EF=,∠QFE=,故EH=,即原点A到平面MCN的距离是.
PAGE
