人教版高中数学选择性必修第一册第三章知识点:抛物线及其标准方程 阶段性测试 (含解析)
文档属性
| 名称 | 人教版高中数学选择性必修第一册第三章知识点:抛物线及其标准方程 阶段性测试 (含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 722.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-02 21:51:52 | ||
图片预览

文档简介
抛物线及其标准方程
(45分钟 100分)
一、选择题(每小题6分,共30分)
1.(2013·大理高二检测)已知抛物线的焦点坐标是F(0,-2),则它的标准方程为
( )
A.y2=8x B.y2=-8x
C.x2=8y D.x2=-8y
2.如果抛物线y2=ax的准线是直线x=1,那么它的焦点坐标为( )
A.(1,0) B.(2,0)
C.(3,0) D.(-1,0)
3.(2013·遵义高二检测)以坐标轴为对称轴,以原点为顶点且过圆x2+y2-2x+
6y+9=0的圆心的抛物线的方程是( )
A.y=3x2或y=-3x2 B.y=3x2
C.y2=-9x或y=3x2 D.y=-3x2或y2=9x
4.抛物线y2=12x上与焦点的距离等于8的点的横坐标是( )
A.5 B.4 C.3 D.2
5.(2013·汝阳高二检测)一个动圆的圆心在抛物线y2=8x上,且动圆恒与直线x+2=0相切,则动圆必过定点( )
A.(0,2) B.(0,-2) C.(2,0) D.(4,0)
二、填空题(每小题8分,共24分)
6.(2013·安阳高二检测)抛物线y=4x2上的一点M到焦点的距离为1,则点M的 纵坐标是 .
7.已知抛物线y2=2px的准线与圆(x-3)2+y2=16相切,则p的值为 .
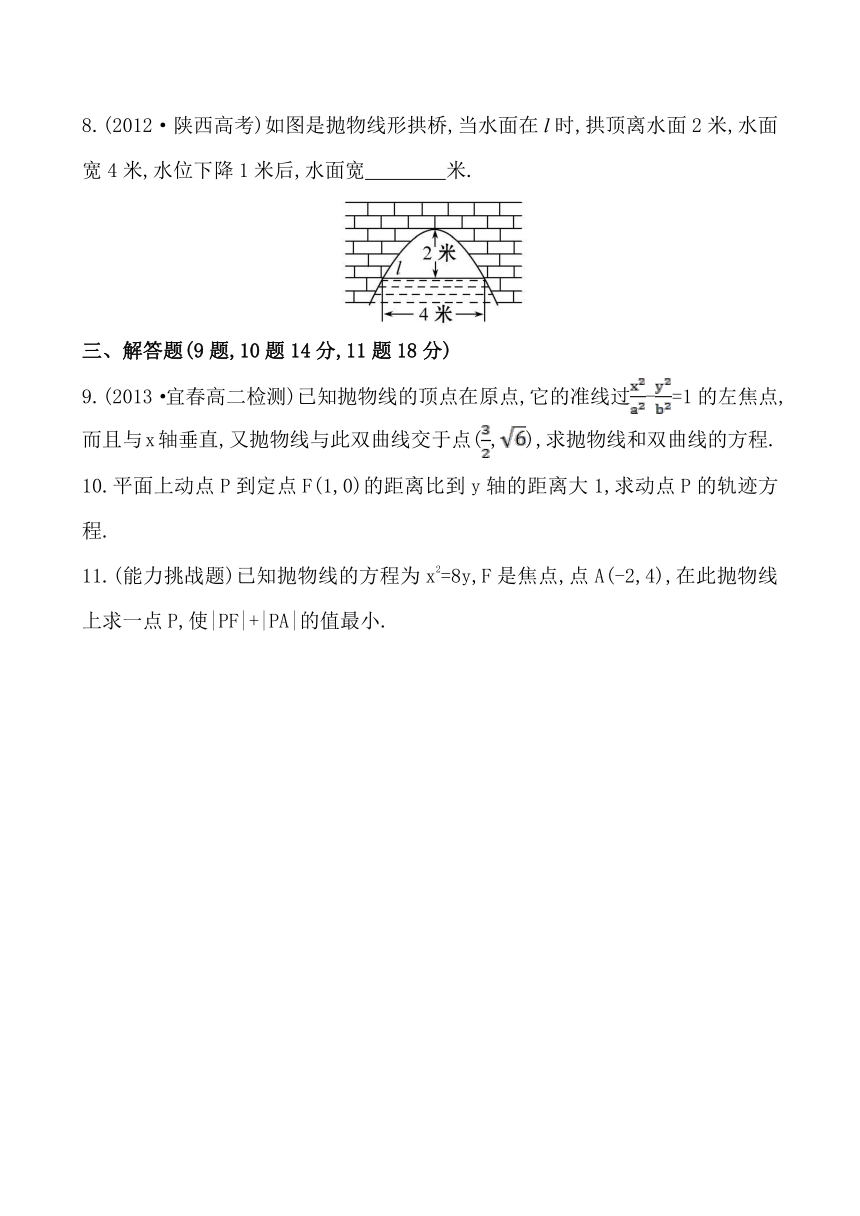
8.(2012·陕西高考)如图是抛物线形拱桥,当水面在l时,拱顶离水面2米,水面宽4米,水位下降1米后,水面宽 米.
三、解答题(9题,10题14分,11题18分)
9.(2013·宜春高二检测)已知抛物线的顶点在原点,它的准线过-=1的左焦点,而且与x轴垂直,又抛物线与此双曲线交于点(,),求抛物线和双曲线的方程.
10.平面上动点P到定点F(1,0)的距离比到y轴的距离大1,求动点P的轨迹方程.
11.(能力挑战题)已知抛物线的方程为x2=8y,F是焦点,点A(-2,4),在此抛物线上求一点P,使|PF|+|PA|的值最小.
答案解析
1.【解析】选D.由条件可知,抛物线的焦点在y轴负半轴上,且=2,∴p=4,所以它的标准方程为x2=-8y.
【举一反三】把题中条件改为“准线方程为x=-7”,它的标准方程如何
【解析】由条件可知=7,即p=14.∵准线方程为x=-7,∴焦点是x轴正半轴上的(7,0)点,故方程为y2=28x.
2.【解析】选D.由y2=ax的准线方程为x=-得,-=1,
∴a=-4,从而抛物线方程为y2=-4x,其焦点为(-1,0).
3.【解析】选D.圆x2+y2-2x+6y+9=0的圆心为(1,-3),设抛物线方程为y2=ax或x2=by,把(1,-3)代入并解得a=9,b=-,∴方程为y2=9x或y=-3x2.
4.【解析】选A.由题知抛物线的准线方程为x=-3,设P(x,y),则x+3=8,∴x=5.
5.【解题指南】利用抛物线的定义求解.
【解析】选C.∵y2=8x的准线方程为x=-2,且动圆的圆心在抛物线上.根据抛物线的定义,动圆圆心到直线x=-2的距离等于到焦点的距离,∴动圆必过定点即焦点(2,0).
【变式备选】若动点P到定点(1,1)的距离与到直线2x+y-1=0的距离相等,则P点的轨迹是( )
A.抛物线 B.线段
C.直线 D.射线
【解析】选A.因为点(1,1)不在直线2x+y-1=0上,故点的轨迹是以点(1,1)为焦点,以直线2x+y-1=0为准线的抛物线,故选A.
6.【解题指南】运用方程的思想,列方程组求解.
【解析】抛物线y=4x2的焦点坐标为(0,),设M(x0,y0),
则解得y0=.
答案:
7.【解析】∵抛物线方程为y2=2px,∴其焦点在x轴上,又∵圆(x-3)2+y2=16与x轴的交点为(-1,0)和(7,0),由题意知准线方程为x=-1或x=7,即焦点为(1,0)或(-7,0),
∴=1或-7,解得p=2或-14.
答案:2或-14
8.【解题指南】建立平面直角坐标系,求出抛物线方程,根据方程求解.
【解析】建立适当的坐标系,如图所示,设抛物线方程为x2=-2py(p>0),则点(2,-2)在此抛物线上,代入可求出抛物线的方程是x2=-2y,当y=-3时,x2=-2×(-3)=6,所以x=±,水面宽是2米.
答案:2
9.【解析】设抛物线方程为:y2=2px(p>0),将点(,)代入方程得p=2,所以抛物线方程为:y2=4x.准线方程为:x=-1,由此知道双曲线方程中:c=1;焦点为(-1,0),(1,0),点(,)到两焦点距离之差为2a=1,∴双曲线的方程为:-=1.
10.【解题指南】可以利用直接法求出动点P的轨迹方程,也可以用定义法求轨迹方程.
【解析】方法一:设点P的坐标为(x,y),
则有=|x|+1.
两边平方并化简,得y2=2x+2|x|,
所以y2=
即点P的轨迹方程为y2=
方法二:由题意,动点P到定点F(1,0)的距离比到y轴的距离大1,由于点F(1,0)到y轴的距离为1,故当x<0时,直线y=0(x<0)上的点适合条件;当x≥0时,可以看作是点P到点F(1,0)与到直线x=-1的距离相等,故点P在以点F为焦点,x=-1为准线的抛物线上,其轨迹方程为y2=4x(x≥0).
综上,点P的轨迹方程为y2=
【误区警示】解答本题时,方法一中,距离很容易因忘加绝对值号而出错,方法二也很容易因思考不全面而漏掉x<0的情况.
11.【解题指南】根据抛物线的定义把|PF|转化为点P到准线的距离,画出草图,通过观察图形,利用“数形结合”的思想即可求出点P的坐标.
【解析】∵(-2)2<8×4,∴点A(-2,4)在抛物线x2=8y的内部.
如图,设抛物线的准线为l,过点P作PQ⊥l于点Q,过点A作AB⊥l于点B,
由抛物线的定义可知:|PF|+|PA|=|PQ|+|PA|≥|AQ|≥|AB|,当且仅当P,Q,A三点共线时,|PF|+|PA|取得最小值,即为|AB|.
∵A(-2,4),∴不妨设|PF|+|PA|的值最小时,点P的坐标为(-2,y0),代入x2=8y得y0=,故使|PF|+|PA|的值最小的抛物线上的点P的坐标为(-2,).
PAGE
(45分钟 100分)
一、选择题(每小题6分,共30分)
1.(2013·大理高二检测)已知抛物线的焦点坐标是F(0,-2),则它的标准方程为
( )
A.y2=8x B.y2=-8x
C.x2=8y D.x2=-8y
2.如果抛物线y2=ax的准线是直线x=1,那么它的焦点坐标为( )
A.(1,0) B.(2,0)
C.(3,0) D.(-1,0)
3.(2013·遵义高二检测)以坐标轴为对称轴,以原点为顶点且过圆x2+y2-2x+
6y+9=0的圆心的抛物线的方程是( )
A.y=3x2或y=-3x2 B.y=3x2
C.y2=-9x或y=3x2 D.y=-3x2或y2=9x
4.抛物线y2=12x上与焦点的距离等于8的点的横坐标是( )
A.5 B.4 C.3 D.2
5.(2013·汝阳高二检测)一个动圆的圆心在抛物线y2=8x上,且动圆恒与直线x+2=0相切,则动圆必过定点( )
A.(0,2) B.(0,-2) C.(2,0) D.(4,0)
二、填空题(每小题8分,共24分)
6.(2013·安阳高二检测)抛物线y=4x2上的一点M到焦点的距离为1,则点M的 纵坐标是 .
7.已知抛物线y2=2px的准线与圆(x-3)2+y2=16相切,则p的值为 .
8.(2012·陕西高考)如图是抛物线形拱桥,当水面在l时,拱顶离水面2米,水面宽4米,水位下降1米后,水面宽 米.
三、解答题(9题,10题14分,11题18分)
9.(2013·宜春高二检测)已知抛物线的顶点在原点,它的准线过-=1的左焦点,而且与x轴垂直,又抛物线与此双曲线交于点(,),求抛物线和双曲线的方程.
10.平面上动点P到定点F(1,0)的距离比到y轴的距离大1,求动点P的轨迹方程.
11.(能力挑战题)已知抛物线的方程为x2=8y,F是焦点,点A(-2,4),在此抛物线上求一点P,使|PF|+|PA|的值最小.
答案解析
1.【解析】选D.由条件可知,抛物线的焦点在y轴负半轴上,且=2,∴p=4,所以它的标准方程为x2=-8y.
【举一反三】把题中条件改为“准线方程为x=-7”,它的标准方程如何
【解析】由条件可知=7,即p=14.∵准线方程为x=-7,∴焦点是x轴正半轴上的(7,0)点,故方程为y2=28x.
2.【解析】选D.由y2=ax的准线方程为x=-得,-=1,
∴a=-4,从而抛物线方程为y2=-4x,其焦点为(-1,0).
3.【解析】选D.圆x2+y2-2x+6y+9=0的圆心为(1,-3),设抛物线方程为y2=ax或x2=by,把(1,-3)代入并解得a=9,b=-,∴方程为y2=9x或y=-3x2.
4.【解析】选A.由题知抛物线的准线方程为x=-3,设P(x,y),则x+3=8,∴x=5.
5.【解题指南】利用抛物线的定义求解.
【解析】选C.∵y2=8x的准线方程为x=-2,且动圆的圆心在抛物线上.根据抛物线的定义,动圆圆心到直线x=-2的距离等于到焦点的距离,∴动圆必过定点即焦点(2,0).
【变式备选】若动点P到定点(1,1)的距离与到直线2x+y-1=0的距离相等,则P点的轨迹是( )
A.抛物线 B.线段
C.直线 D.射线
【解析】选A.因为点(1,1)不在直线2x+y-1=0上,故点的轨迹是以点(1,1)为焦点,以直线2x+y-1=0为准线的抛物线,故选A.
6.【解题指南】运用方程的思想,列方程组求解.
【解析】抛物线y=4x2的焦点坐标为(0,),设M(x0,y0),
则解得y0=.
答案:
7.【解析】∵抛物线方程为y2=2px,∴其焦点在x轴上,又∵圆(x-3)2+y2=16与x轴的交点为(-1,0)和(7,0),由题意知准线方程为x=-1或x=7,即焦点为(1,0)或(-7,0),
∴=1或-7,解得p=2或-14.
答案:2或-14
8.【解题指南】建立平面直角坐标系,求出抛物线方程,根据方程求解.
【解析】建立适当的坐标系,如图所示,设抛物线方程为x2=-2py(p>0),则点(2,-2)在此抛物线上,代入可求出抛物线的方程是x2=-2y,当y=-3时,x2=-2×(-3)=6,所以x=±,水面宽是2米.
答案:2
9.【解析】设抛物线方程为:y2=2px(p>0),将点(,)代入方程得p=2,所以抛物线方程为:y2=4x.准线方程为:x=-1,由此知道双曲线方程中:c=1;焦点为(-1,0),(1,0),点(,)到两焦点距离之差为2a=1,∴双曲线的方程为:-=1.
10.【解题指南】可以利用直接法求出动点P的轨迹方程,也可以用定义法求轨迹方程.
【解析】方法一:设点P的坐标为(x,y),
则有=|x|+1.
两边平方并化简,得y2=2x+2|x|,
所以y2=
即点P的轨迹方程为y2=
方法二:由题意,动点P到定点F(1,0)的距离比到y轴的距离大1,由于点F(1,0)到y轴的距离为1,故当x<0时,直线y=0(x<0)上的点适合条件;当x≥0时,可以看作是点P到点F(1,0)与到直线x=-1的距离相等,故点P在以点F为焦点,x=-1为准线的抛物线上,其轨迹方程为y2=4x(x≥0).
综上,点P的轨迹方程为y2=
【误区警示】解答本题时,方法一中,距离很容易因忘加绝对值号而出错,方法二也很容易因思考不全面而漏掉x<0的情况.
11.【解题指南】根据抛物线的定义把|PF|转化为点P到准线的距离,画出草图,通过观察图形,利用“数形结合”的思想即可求出点P的坐标.
【解析】∵(-2)2<8×4,∴点A(-2,4)在抛物线x2=8y的内部.
如图,设抛物线的准线为l,过点P作PQ⊥l于点Q,过点A作AB⊥l于点B,
由抛物线的定义可知:|PF|+|PA|=|PQ|+|PA|≥|AQ|≥|AB|,当且仅当P,Q,A三点共线时,|PF|+|PA|取得最小值,即为|AB|.
∵A(-2,4),∴不妨设|PF|+|PA|的值最小时,点P的坐标为(-2,y0),代入x2=8y得y0=,故使|PF|+|PA|的值最小的抛物线上的点P的坐标为(-2,).
PAGE
