天津市和平区2023-2024学年高二下学期期末质量调查数学试卷(PDF版无答案)
文档属性
| 名称 | 天津市和平区2023-2024学年高二下学期期末质量调查数学试卷(PDF版无答案) | 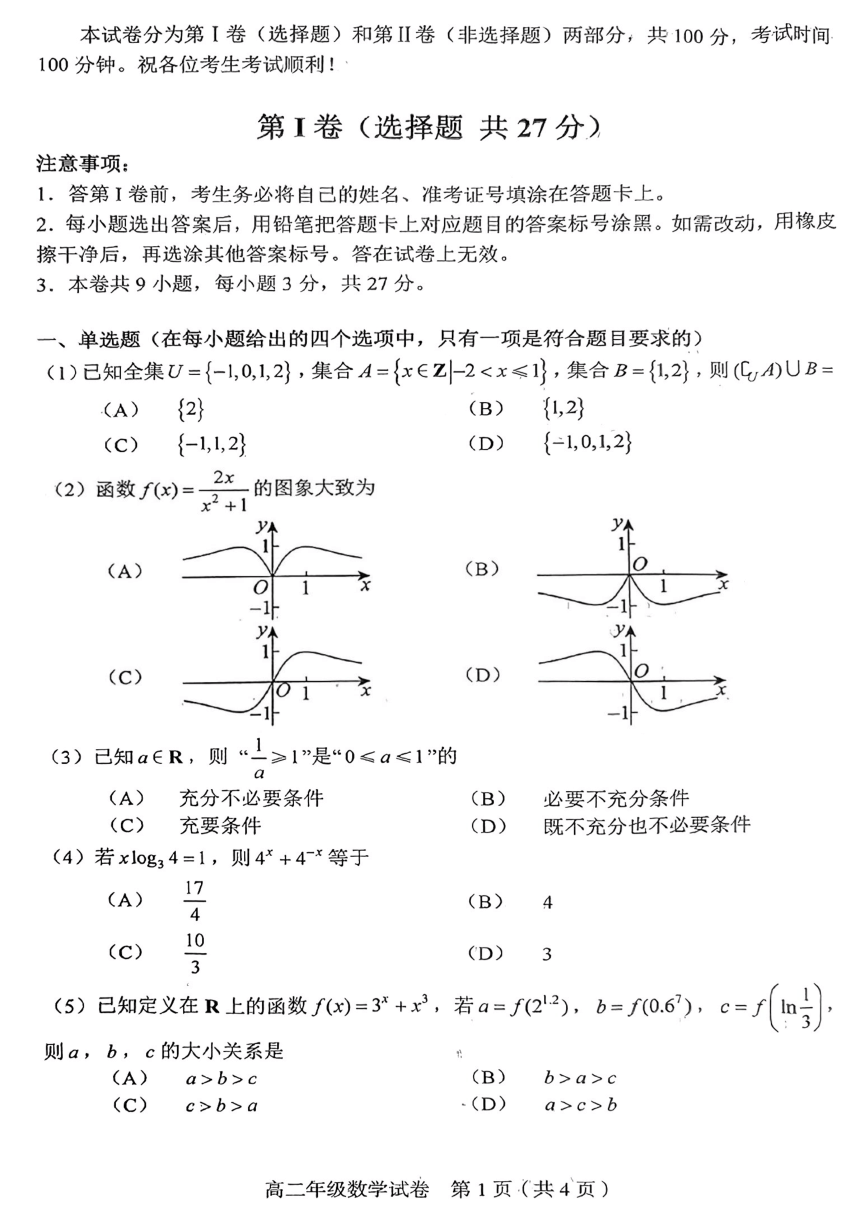 | |
| 格式 | |||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-03 07:30:45 | ||
图片预览


文档简介
(2)函数f四=2x的图象大致为
x2+1
(A)
(B)
y
C)
(D)
(6)某公司研发新产品投入金额x(单位:万元)与该产品的收益y(单位:万元)的
5组统计数据如下表所示.由表中数据用最小二乘法求得投入金额x与收益y满足经验
回归方程)=2.5x+a,则下列结论不正确的是
5
7
8
9
11
y
16
22
24
27
31
(A)
x与y有正相关关系
(B)
a=4
(C)
当新产品投入金额为6万元时,该产品的收益大约为19万元
(D)
当x=11时,残差为0.5(残差=观测值-预测值)
(7)为研究吸烟是否与肺癌有关,某肿瘤研究所采取有放回简单随机抽样的方法,调查
了100人,得到成对样本观测数据的分类统计结果,如下列联表所示(单位:人),根
据数据计算得x2≈22.161,依据小概率值=0.001的独立性检验,小概率值u=0.001相
应的临界值为x0.01=10.828,则下列结论不正确的是
肺癌
吸烟
合计
非肺癌患者
肺癌患者
非吸烟者
25
10
35
吸烟者
15
m
65
合计
40
60
100
(A)
m=50
(B)
若从这100人中随机抽取2人,则2人都是非肺癌患者的概率为26
165
(c)
在犯错误的概率不超过0.001的前提下,认为吸烟与患肺癌有关联
(D)
在犯错误的概率不超过0.001的前提下,认为吸烟与患肺癌无关联
(8)已知函数fx)=x2-2x,g(x)=lnx+a,3x∈[0,3],2∈[L,2],使得f(x)≤g(x2)
成立,则实数a的取值范围是
(A)
(-0,-1]
(B)
[-1,+o)
(C)
(-o,-1.-ln2]
(D)
[-1-ln2,+o)
(9)有如下5个命题:
①记知随机变量X-叫5号引,
则PX=2)=40
D(3X)=10;
243
②已知随机变量Y~NL,σ2),若P(Y>3)=0.2,则P(Y-≤2)=0.6:
③已知命题p:x>0,sinx0,sinx≥x;
④函数f(x)=Inx+2x-6在区间(2,3)内有且仅有1个零点:
③通数+的最小值为9,
将上述5个命题重新排序,其中假命题不在首尾两个位置,则排序方法有
(A)72种
(B)
36种
(C)
18种
(D)
12种
高二年级数学试卷第2页(共4页)
第Ⅱ卷(非选择题共73分)
注意事项:
1.用黑色墨水的钢笔或签字笔将答案写在答题卡上。
2.本卷共10小题,共73分。
二、填空题(本大题共6小题,每小题4分,共24分。试题中包含两个空的,答对1个的
给2分,全部答对的给4分)
(10)在
安2
的展开式中,x的系数为·(请用数字作答)
(11)
已知函数f满足=sinx+f()osx+2x,则=一
(12)某校举办“中华颂”朗诵比赛,现有3名男生和3名女生报名,需将这6名同学
分为3组,每组由1名男生和1名女生组成,则有种分组方法.(请用数字作答)
(13)甲和乙两个箱子中各装有5个大小相同的小球,其中甲箱中有2个红球、3个白
球,乙箱中有4个红球、1个白球.()从甲箱中随机抽出2个球,在已知抽到白球的
条件下,则2个球都是白球的概率为;()掷一枚质地均匀的骰子,如果点数小
于等于2,就从甲箱中随机抽出1个球;如果点数大于等于3,就从乙箱中随机抽出1
个球,则抽到红球的概率为一·
(14)若函数f(x)=ln(e*-x-1)在(0,+o)上单调递增,则实数a的最大值为
(15)已知函数=,g)-nx-m,若g在区间[+
上有且仅有1
个零点,则实数m的取值范围为
三、解答题(本大题共5小题,共49分,解答应写出文字说明,证明过程或演算步骤)
(16)(本小题满分9分)
知x)=x2-x2-2x+1的两个极值点分别是x=-1,为=2
(I)求实数a,b的值;
(IⅡ)求函数f(x)的单调区间.
3(4
x2+1
(A)
(B)
y
C)
(D)
(6)某公司研发新产品投入金额x(单位:万元)与该产品的收益y(单位:万元)的
5组统计数据如下表所示.由表中数据用最小二乘法求得投入金额x与收益y满足经验
回归方程)=2.5x+a,则下列结论不正确的是
5
7
8
9
11
y
16
22
24
27
31
(A)
x与y有正相关关系
(B)
a=4
(C)
当新产品投入金额为6万元时,该产品的收益大约为19万元
(D)
当x=11时,残差为0.5(残差=观测值-预测值)
(7)为研究吸烟是否与肺癌有关,某肿瘤研究所采取有放回简单随机抽样的方法,调查
了100人,得到成对样本观测数据的分类统计结果,如下列联表所示(单位:人),根
据数据计算得x2≈22.161,依据小概率值=0.001的独立性检验,小概率值u=0.001相
应的临界值为x0.01=10.828,则下列结论不正确的是
肺癌
吸烟
合计
非肺癌患者
肺癌患者
非吸烟者
25
10
35
吸烟者
15
m
65
合计
40
60
100
(A)
m=50
(B)
若从这100人中随机抽取2人,则2人都是非肺癌患者的概率为26
165
(c)
在犯错误的概率不超过0.001的前提下,认为吸烟与患肺癌有关联
(D)
在犯错误的概率不超过0.001的前提下,认为吸烟与患肺癌无关联
(8)已知函数fx)=x2-2x,g(x)=lnx+a,3x∈[0,3],2∈[L,2],使得f(x)≤g(x2)
成立,则实数a的取值范围是
(A)
(-0,-1]
(B)
[-1,+o)
(C)
(-o,-1.-ln2]
(D)
[-1-ln2,+o)
(9)有如下5个命题:
①记知随机变量X-叫5号引,
则PX=2)=40
D(3X)=10;
243
②已知随机变量Y~NL,σ2),若P(Y>3)=0.2,则P(Y-≤2)=0.6:
③已知命题p:x>0,sinx
④函数f(x)=Inx+2x-6在区间(2,3)内有且仅有1个零点:
③通数+的最小值为9,
将上述5个命题重新排序,其中假命题不在首尾两个位置,则排序方法有
(A)72种
(B)
36种
(C)
18种
(D)
12种
高二年级数学试卷第2页(共4页)
第Ⅱ卷(非选择题共73分)
注意事项:
1.用黑色墨水的钢笔或签字笔将答案写在答题卡上。
2.本卷共10小题,共73分。
二、填空题(本大题共6小题,每小题4分,共24分。试题中包含两个空的,答对1个的
给2分,全部答对的给4分)
(10)在
安2
的展开式中,x的系数为·(请用数字作答)
(11)
已知函数f满足=sinx+f()osx+2x,则=一
(12)某校举办“中华颂”朗诵比赛,现有3名男生和3名女生报名,需将这6名同学
分为3组,每组由1名男生和1名女生组成,则有种分组方法.(请用数字作答)
(13)甲和乙两个箱子中各装有5个大小相同的小球,其中甲箱中有2个红球、3个白
球,乙箱中有4个红球、1个白球.()从甲箱中随机抽出2个球,在已知抽到白球的
条件下,则2个球都是白球的概率为;()掷一枚质地均匀的骰子,如果点数小
于等于2,就从甲箱中随机抽出1个球;如果点数大于等于3,就从乙箱中随机抽出1
个球,则抽到红球的概率为一·
(14)若函数f(x)=ln(e*-x-1)在(0,+o)上单调递增,则实数a的最大值为
(15)已知函数=,g)-nx-m,若g在区间[+
上有且仅有1
个零点,则实数m的取值范围为
三、解答题(本大题共5小题,共49分,解答应写出文字说明,证明过程或演算步骤)
(16)(本小题满分9分)
知x)=x2-x2-2x+1的两个极值点分别是x=-1,为=2
(I)求实数a,b的值;
(IⅡ)求函数f(x)的单调区间.
3(4
同课章节目录
