初中数学人教版八年级下册20.1 数据的集中趋势(第 2课时 ) 中位数和众数(含答案)
文档属性
| 名称 | 初中数学人教版八年级下册20.1 数据的集中趋势(第 2课时 ) 中位数和众数(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 390.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-03 00:00:00 | ||
图片预览


文档简介
第 2课时 中位数和众数
基础知识夯实
知识沉淀
1.中位数:将一组数据按从小到大(或从大到小)顺序排列,如果数据的个数是奇数,则称处于 位置的数为这组数据的中位数;如果数据的个数是偶数,则称中间两个数据的 为这组数据的中位数.
2.众数:在一组数据中出现 的数据称为这组数据的众数.
基础过关
1.若一组数据2,4,x,5,7的平均数为5,则这组数据中的x和中位数分别为 ( )
A.5,7 B.5,5
C.7,5 D.7,7
2.在 2019年的体育中考中,某校 6 名学生的体育成绩统计如图,则这组数据的众数是 分;中位数是 分.
典型案例探究
知识点1 中位数
【例题1】某校共有 40名初中生参加足球兴趣小组,他们的年龄统计情况如图,则这 40 名学生年龄的中位数是 ( )
A.12 岁 B.13 岁
C.14岁 D.15 岁
【变式1】李大伯前年在驻村扶贫工作队的帮助下种了一片果林,今年收获一批成熟的果子.他选取了5棵果树,采摘后分别称重.每棵果树果子总质量(单位:kg)分别为:90,100,120,110,80.这五个数据的中位数是 ( )
A.120 B.110
C.100 D.90
知识点 2 众数
【例题2】某中学篮球队12名队员的年龄情况如下:
年龄/岁 14 15 16 17 18
人数 1 5 3 2 1
则这个队队员年龄的众数和中位数分别是 ( )
A.15,16 B.15,15
C.15,15.5 D.16,15
【变式2】某小组7 名学生的中考体育分数如下:37,40,39,37,40,38,40,该组数据的众数、中位数分别为 ( )
A.40,37 B.40,39
C.39,40 D.40,38
知识点3 众数、中位数与平均数的应用
【例题3】某企业生产部统计了15名工人某月的加工零件数:
每人加工零件数 540 450 300 240 210 120
人数 1 1 2 6 3 2
(1)求出这15 人该月加工零件数的平均数并直接写出中位数和众数;
(2)若生产部领导把每位工人的月加工零件数定为260件,你认为合理否,为什么
【变式3】(2019·达州)随机抽取某小吃店一周的营业额(单位:元)如下表:
星期一 星期二 星期三 星期四 星期五 星期六| 星期日 合计
540 680 640 640 780 1 110 1 070 5 460
(1)分析数据,填空:这组数据的平均数是 元,中位数是 元,众数是 元;
(2)估计一个月的营业额(按30天计算):
①星期一到星期五营业额相差不大,用这5天的平均数估算合适么
答: (填“合适”或“不合适”);
②选择一个你认为最合适的数据估算这个小吃店一个月的营业额.
课后作业
A 组
1.在开展“爱心捐助某灾区”的活动中,某团支部8名团员捐款的数额(单位:元)分别为3,5,6,5,5,6,5,10,这组数据的中位数是 ( )
A.3元 B.5 元 C.6 元 D.10元
2.已知一组数据6,8,10,x的中位数与平均数相等,这样的x有 ( )
A.1 个 B.2 个
C.3个 D.4个以上(含 4个)
3.一名射击爱好者 5次射击的中靶环数如下:6,7,9,8,9.这5个数据的众数是 ( )
A.6 B.7 C.8 D.9
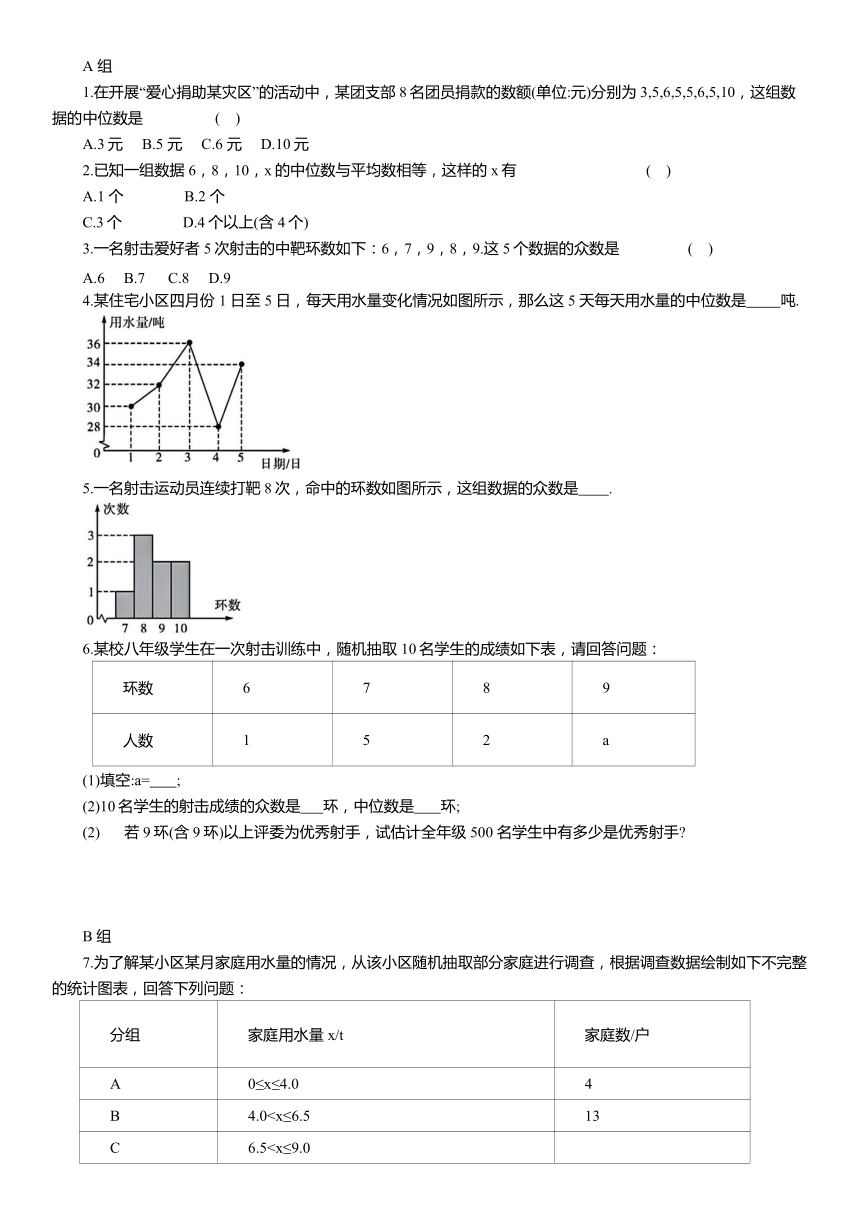
4.某住宅小区四月份 1 日至 5 日,每天用水量变化情况如图所示,那么这 5 天每天用水量的中位数是 吨.
5.一名射击运动员连续打靶8次,命中的环数如图所示,这组数据的众数是 .
6.某校八年级学生在一次射击训练中,随机抽取10名学生的成绩如下表,请回答问题:
环数 6 7 8 9
人数 1 5 2 a
(1)填空:a= ;
(2)10名学生的射击成绩的众数是 环,中位数是 环;
若9环(含 9环)以上评委为优秀射手,试估计全年级500 名学生中有多少是优秀射手
B 组
7.为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,根据调查数据绘制如下不完整的统计图表,回答下列问题:
分组 家庭用水量 x/t 家庭数/户
A 0≤x≤4.0 4
B 4.0C 6.5D 9.0E 11.5F x>14.0 3
(1)本次调查的家庭数为 户,C 组的家庭数为 户,D组的家庭数为 户;
(2)家庭用水量的中位数落在 组;
(3)若该小区共有200 户家庭,请估计该月用水量不超过9.0 t的家庭数.
8.在某校组织的知识竞赛中,每班参加比赛的人数相同,成绩分为A,B,C,D 四个等级,其中相应等级的得分依次记为100分,90分,80 分,70 分,学校将某年级的(1)班和(2)班的成绩整理并绘制成如图的统计图.
请你根据以上提供的信息解答下列问题:
(1)此次竞赛(2)班成绩在C级以上(包括C级)的人数多少
(2)请你将下表补充完整;
(3)根据下表,请你比较这两个班这次竞赛成绩.
班级 成绩
平均分/分 中位数/分 众数/分
(1)班 90
(2)班 87.6 100
C 组
9.某商场甲、乙、丙三名业务员 2019年前5个月的销售额(单位:万元)如下表:
业务员 销售额/万元
1 月 2 月 3月 4 月 5 月
甲 9 9 8 7 5
乙 10 9 6 8 8
丙 11 10 5 5 9
(1)根据上表中的数据,将表补充完整:
业务员 平均数/万元 众数/万元 中位数/万元
甲 7.6 8
乙 8 8
丙 8 5
甲、乙、丙三名业务员都说自己的销售业绩好,你赞同谁的说法 请说明理由.
第 2 课时 中位数和众数
【基础知识夯实】
知识沉淀
1.中间 平均数 2.次数最多
基础过关
1. C 2.47 47
【典型案例探究】
例题1 C 变式1 C 例题 2 (C 变式 2 B
例题3 解: 240×6+210×3+120×2)=260(件),中位数是240件.众数是240件.
(2)不合适,因为表中数据显示,每月能完成260件的人数一共是4人,还有11人不能达到此定额,尽管260是平均数,但不利于调动多数员工的积极性.
变式3 解:(1)这组数据的平均数 (元).
按照从小到大排列为 540,640,640,680,780,1 070,1 110,
中位数为680元,众数为640 元.
故答案为:780,680,640;
(2)①因为在周一至周日的营业额中周六、日的营业额明显高于其他五天的营业额,
所以去掉周六、日的营业额对平均数的影响较大,
故用该店本周星期一到星期五的日平均营业额估计当月的营业总额不合适.
故答案为:不合适;
②用该店本周一到周日的日均营业额估计当月营业额,当月的营业额为 30×780=23 400(元).
【课后作业】
1. B 2. C 3. D 4.32 5.8
6.解:(1)10-1-5-2=2人,故答案为2.
(2)成绩为7 环的人数最多,是5人,因此成绩的众数为7 环.
将这10人的射击成绩从小到大排列后,处在第5、6位的两个数都是7环,因此中位数是7环.
故答案为:7,7.
(人).
答:全年级500名学生中大约有 100人是优秀射手.
7.解:(1)调查的家庭数为 13÷26%=50.
C组的家庭数为 50×30%=15.
D组的家庭数为50-4-13-6-3-15=9.
(2)调查的家庭数为50户,则中位数为第25、26 户的平均数,从表格观察都落在C 组.
(3)调查家庭中不超过9.0t 的户数有4+13+15=32, (户).
8.解:(1)(2)班成绩在 C级以上(包括C级)的人数有(6+12+2+5)×(44%+4%+36%)=21(人).
(2)(1)班平均分为: =87.6(分),
(2)班A等级(100分)的人数为:25×44%=11(人),
B等级(90分)的人数为:25×4%=1(人),
C等级(80分)的人数为:25×36%=9(人),
D等级(70分)的人数为:25×16%=4(人),
则(2)班成绩的中位数为:80分,
(1)班成绩的众数为:90分,补全表格如下:
级级 平均数/分 中位数/分 众数/分
(1)班 87.6 90 90
(2)班 87.6 80 100
故答案为:87.6,90,80;
(3)①从平均数的角度看两班成绩一样,从中位数的角度看(1)班比(2)班的成绩好;
②从平均数的角度看两班成绩一样,从众数的角度看(2)班比(1)班的成绩好.
9.解:(1)由题意可得,甲的众数是9.
乙的平均数是
丙的中位数是 9.
(2)我赞同乙的说法,理由:由表格可知,乙的平均数最高,可知乙的总体业绩最好,故乙的销售业绩好.
基础知识夯实
知识沉淀
1.中位数:将一组数据按从小到大(或从大到小)顺序排列,如果数据的个数是奇数,则称处于 位置的数为这组数据的中位数;如果数据的个数是偶数,则称中间两个数据的 为这组数据的中位数.
2.众数:在一组数据中出现 的数据称为这组数据的众数.
基础过关
1.若一组数据2,4,x,5,7的平均数为5,则这组数据中的x和中位数分别为 ( )
A.5,7 B.5,5
C.7,5 D.7,7
2.在 2019年的体育中考中,某校 6 名学生的体育成绩统计如图,则这组数据的众数是 分;中位数是 分.
典型案例探究
知识点1 中位数
【例题1】某校共有 40名初中生参加足球兴趣小组,他们的年龄统计情况如图,则这 40 名学生年龄的中位数是 ( )
A.12 岁 B.13 岁
C.14岁 D.15 岁
【变式1】李大伯前年在驻村扶贫工作队的帮助下种了一片果林,今年收获一批成熟的果子.他选取了5棵果树,采摘后分别称重.每棵果树果子总质量(单位:kg)分别为:90,100,120,110,80.这五个数据的中位数是 ( )
A.120 B.110
C.100 D.90
知识点 2 众数
【例题2】某中学篮球队12名队员的年龄情况如下:
年龄/岁 14 15 16 17 18
人数 1 5 3 2 1
则这个队队员年龄的众数和中位数分别是 ( )
A.15,16 B.15,15
C.15,15.5 D.16,15
【变式2】某小组7 名学生的中考体育分数如下:37,40,39,37,40,38,40,该组数据的众数、中位数分别为 ( )
A.40,37 B.40,39
C.39,40 D.40,38
知识点3 众数、中位数与平均数的应用
【例题3】某企业生产部统计了15名工人某月的加工零件数:
每人加工零件数 540 450 300 240 210 120
人数 1 1 2 6 3 2
(1)求出这15 人该月加工零件数的平均数并直接写出中位数和众数;
(2)若生产部领导把每位工人的月加工零件数定为260件,你认为合理否,为什么
【变式3】(2019·达州)随机抽取某小吃店一周的营业额(单位:元)如下表:
星期一 星期二 星期三 星期四 星期五 星期六| 星期日 合计
540 680 640 640 780 1 110 1 070 5 460
(1)分析数据,填空:这组数据的平均数是 元,中位数是 元,众数是 元;
(2)估计一个月的营业额(按30天计算):
①星期一到星期五营业额相差不大,用这5天的平均数估算合适么
答: (填“合适”或“不合适”);
②选择一个你认为最合适的数据估算这个小吃店一个月的营业额.
课后作业
A 组
1.在开展“爱心捐助某灾区”的活动中,某团支部8名团员捐款的数额(单位:元)分别为3,5,6,5,5,6,5,10,这组数据的中位数是 ( )
A.3元 B.5 元 C.6 元 D.10元
2.已知一组数据6,8,10,x的中位数与平均数相等,这样的x有 ( )
A.1 个 B.2 个
C.3个 D.4个以上(含 4个)
3.一名射击爱好者 5次射击的中靶环数如下:6,7,9,8,9.这5个数据的众数是 ( )
A.6 B.7 C.8 D.9
4.某住宅小区四月份 1 日至 5 日,每天用水量变化情况如图所示,那么这 5 天每天用水量的中位数是 吨.
5.一名射击运动员连续打靶8次,命中的环数如图所示,这组数据的众数是 .
6.某校八年级学生在一次射击训练中,随机抽取10名学生的成绩如下表,请回答问题:
环数 6 7 8 9
人数 1 5 2 a
(1)填空:a= ;
(2)10名学生的射击成绩的众数是 环,中位数是 环;
若9环(含 9环)以上评委为优秀射手,试估计全年级500 名学生中有多少是优秀射手
B 组
7.为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,根据调查数据绘制如下不完整的统计图表,回答下列问题:
分组 家庭用水量 x/t 家庭数/户
A 0≤x≤4.0 4
B 4.0
(1)本次调查的家庭数为 户,C 组的家庭数为 户,D组的家庭数为 户;
(2)家庭用水量的中位数落在 组;
(3)若该小区共有200 户家庭,请估计该月用水量不超过9.0 t的家庭数.
8.在某校组织的知识竞赛中,每班参加比赛的人数相同,成绩分为A,B,C,D 四个等级,其中相应等级的得分依次记为100分,90分,80 分,70 分,学校将某年级的(1)班和(2)班的成绩整理并绘制成如图的统计图.
请你根据以上提供的信息解答下列问题:
(1)此次竞赛(2)班成绩在C级以上(包括C级)的人数多少
(2)请你将下表补充完整;
(3)根据下表,请你比较这两个班这次竞赛成绩.
班级 成绩
平均分/分 中位数/分 众数/分
(1)班 90
(2)班 87.6 100
C 组
9.某商场甲、乙、丙三名业务员 2019年前5个月的销售额(单位:万元)如下表:
业务员 销售额/万元
1 月 2 月 3月 4 月 5 月
甲 9 9 8 7 5
乙 10 9 6 8 8
丙 11 10 5 5 9
(1)根据上表中的数据,将表补充完整:
业务员 平均数/万元 众数/万元 中位数/万元
甲 7.6 8
乙 8 8
丙 8 5
甲、乙、丙三名业务员都说自己的销售业绩好,你赞同谁的说法 请说明理由.
第 2 课时 中位数和众数
【基础知识夯实】
知识沉淀
1.中间 平均数 2.次数最多
基础过关
1. C 2.47 47
【典型案例探究】
例题1 C 变式1 C 例题 2 (C 变式 2 B
例题3 解: 240×6+210×3+120×2)=260(件),中位数是240件.众数是240件.
(2)不合适,因为表中数据显示,每月能完成260件的人数一共是4人,还有11人不能达到此定额,尽管260是平均数,但不利于调动多数员工的积极性.
变式3 解:(1)这组数据的平均数 (元).
按照从小到大排列为 540,640,640,680,780,1 070,1 110,
中位数为680元,众数为640 元.
故答案为:780,680,640;
(2)①因为在周一至周日的营业额中周六、日的营业额明显高于其他五天的营业额,
所以去掉周六、日的营业额对平均数的影响较大,
故用该店本周星期一到星期五的日平均营业额估计当月的营业总额不合适.
故答案为:不合适;
②用该店本周一到周日的日均营业额估计当月营业额,当月的营业额为 30×780=23 400(元).
【课后作业】
1. B 2. C 3. D 4.32 5.8
6.解:(1)10-1-5-2=2人,故答案为2.
(2)成绩为7 环的人数最多,是5人,因此成绩的众数为7 环.
将这10人的射击成绩从小到大排列后,处在第5、6位的两个数都是7环,因此中位数是7环.
故答案为:7,7.
(人).
答:全年级500名学生中大约有 100人是优秀射手.
7.解:(1)调查的家庭数为 13÷26%=50.
C组的家庭数为 50×30%=15.
D组的家庭数为50-4-13-6-3-15=9.
(2)调查的家庭数为50户,则中位数为第25、26 户的平均数,从表格观察都落在C 组.
(3)调查家庭中不超过9.0t 的户数有4+13+15=32, (户).
8.解:(1)(2)班成绩在 C级以上(包括C级)的人数有(6+12+2+5)×(44%+4%+36%)=21(人).
(2)(1)班平均分为: =87.6(分),
(2)班A等级(100分)的人数为:25×44%=11(人),
B等级(90分)的人数为:25×4%=1(人),
C等级(80分)的人数为:25×36%=9(人),
D等级(70分)的人数为:25×16%=4(人),
则(2)班成绩的中位数为:80分,
(1)班成绩的众数为:90分,补全表格如下:
级级 平均数/分 中位数/分 众数/分
(1)班 87.6 90 90
(2)班 87.6 80 100
故答案为:87.6,90,80;
(3)①从平均数的角度看两班成绩一样,从中位数的角度看(1)班比(2)班的成绩好;
②从平均数的角度看两班成绩一样,从众数的角度看(2)班比(1)班的成绩好.
9.解:(1)由题意可得,甲的众数是9.
乙的平均数是
丙的中位数是 9.
(2)我赞同乙的说法,理由:由表格可知,乙的平均数最高,可知乙的总体业绩最好,故乙的销售业绩好.
