初中数学人教版八年级下册第十九章 一次函数 章末整合 感知中考(含答案)
文档属性
| 名称 | 初中数学人教版八年级下册第十九章 一次函数 章末整合 感知中考(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 576.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-03 00:00:00 | ||
图片预览

文档简介
8.函数的图象和性质:
函数名称 解析式 性质
正比例函数 y=kx(k≠0) ①k>0,图象在第一、三象限,y随x 的增大而增大;②k<0,图象在第二、四象限,y随x的增大而减小
一次函数 y=kx+b(k≠0) ①k>0,y随x的增大而增大; ②k<0,y随x的增大而减小
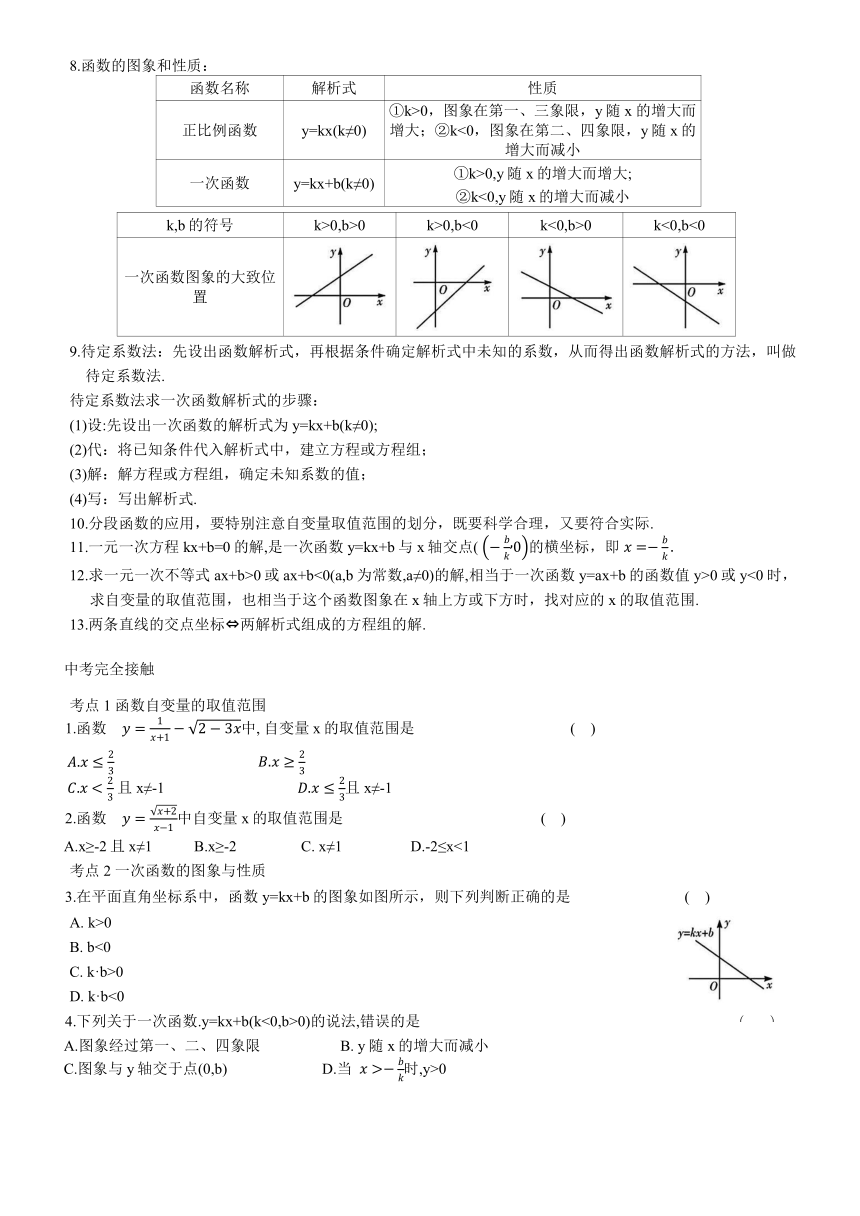
k,b的符号 k>0,b>0 k>0,b<0 k<0,b>0 k<0,b<0
一次函数图象的大致位置
9.待定系数法:先设出函数解析式,再根据条件确定解析式中未知的系数,从而得出函数解析式的方法,叫做待定系数法.
待定系数法求一次函数解析式的步骤:
(1)设:先设出一次函数的解析式为y=kx+b(k≠0);
(2)代:将已知条件代入解析式中,建立方程或方程组;
(3)解:解方程或方程组,确定未知系数的值;
(4)写:写出解析式.
10.分段函数的应用,要特别注意自变量取值范围的划分,既要科学合理,又要符合实际.
11.一元一次方程kx+b=0的解,是一次函数y=kx+b与x轴交点( 的横坐标,即
12.求一元一次不等式ax+b>0或ax+b<0(a,b为常数,a≠0)的解,相当于一次函数y=ax+b的函数值y>0或y<0时,求自变量的取值范围,也相当于这个函数图象在x轴上方或下方时,找对应的x的取值范围.
13.两条直线的交点坐标 两解析式组成的方程组的解.
中考完全接触
考点 1 函数自变量的取值范围
1.函数 中, 自变量x的取值范围是 ( )
且x≠-1 且x≠-1
2.函数 中自变量 x的取值范围是 ( )
A.x≥-2且x≠1 B.x≥-2 C. x≠1 D.-2≤x<1
考点 2 一次函数的图象与性质
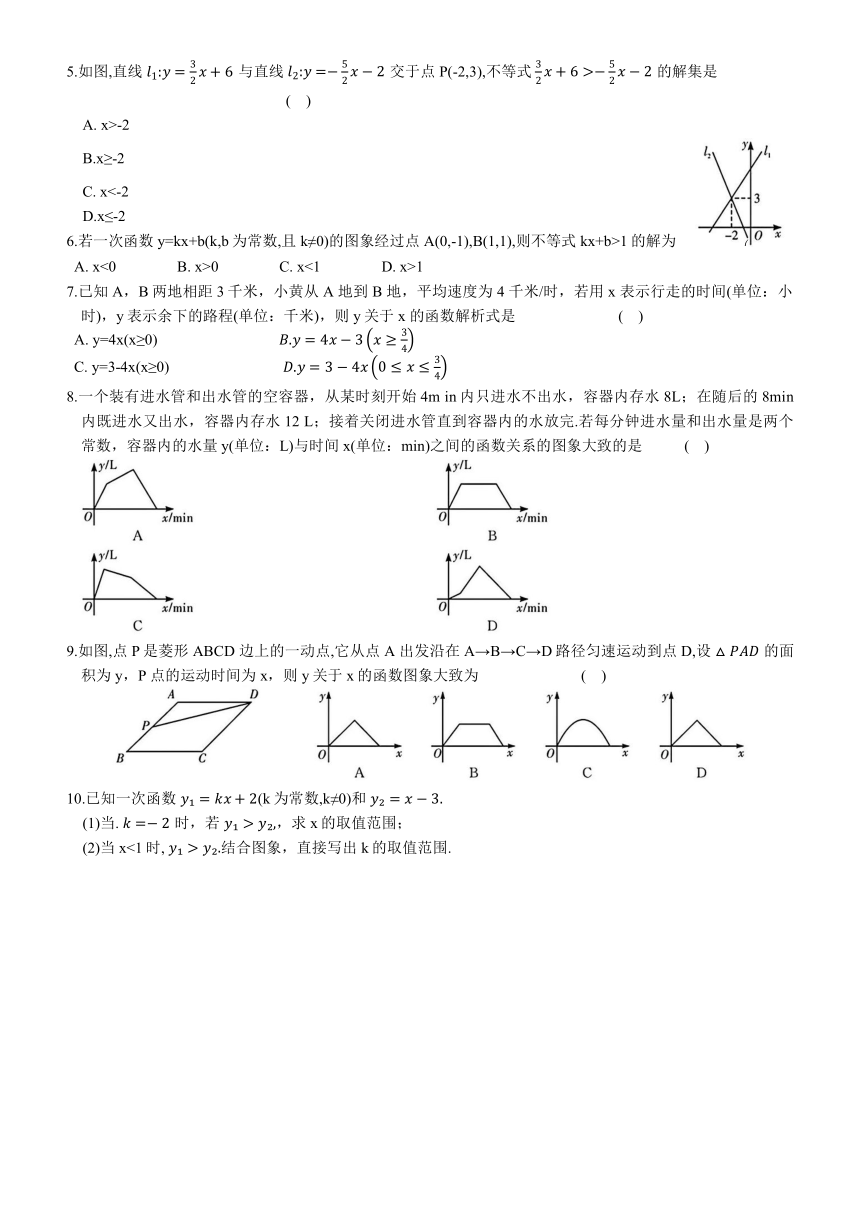
3.在平面直角坐标系中,函数y=kx+b的图象如图所示,则下列判断正确的是 ( )
A. k>0
B. b<0
C. k·b>0
D. k·b<0
4.下列关于一次函数.y=kx+b(k<0,b>0)的说法,错误的是
A.图象经过第一、二、四象限 B. y随x的增大而减小
C.图象与 y轴交于点(0,b) D.当 时,y>0
5.如图,直线 与直线 交于点 P(-2,3),不等式 的解集是 ( )
A. x>-2
B.x≥-2
C. x<-2
D.x≤-2
6.若一次函数y=kx+b(k,b为常数,且k≠0)的图象经过点 A(0,-1),B(1,1),则不等式kx+b>1的解为
A. x<0 B. x>0 C. x<1 D. x>1
7.已知A,B两地相距3千米,小黄从 A 地到 B 地,平均速度为4 千米/时,若用x 表示行走的时间(单位:小时),y表示余下的路程(单位:千米),则y关于x 的函数解析式是 ( )
A. y=4x(x≥0)
C. y=3-4x(x≥0)
8.一个装有进水管和出水管的空容器,从某时刻开始4m in内只进水不出水,容器内存水 8L;在随后的8min内既进水又出水,容器内存水12 L;接着关闭进水管直到容器内的水放完.若每分钟进水量和出水量是两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的函数关系的图象大致的是 ( )
9.如图,点 P是菱形ABCD 边上的一动点,它从点 A 出发沿在A→B→C→D路径匀速运动到点 D,设 的面积为y,P 点的运动时间为x,则y关于x的函数图象大致为 ( )
10.已知一次函数 (k为常数,k≠0)和
(1)当. 时,若 ,求x的取值范围;
(2)当x<1时, 结合图象,直接写出k的取值范围.
考点3 一次函数的平移
11.直线y=3x+1向下平移2个单位,所得直线的解析式是 ( )
A. y=3x+3 B. y=3x-2 C. y=3x+2 D. y=3x-1
12.把函数y=x向上平移3个单位,下列在该平移后的直线上的点是 ( )
A.(2,2) B.(2,3) C.(2,4) D.(2,5)
考点 4 一次函数与方程(组)、不等式的联系
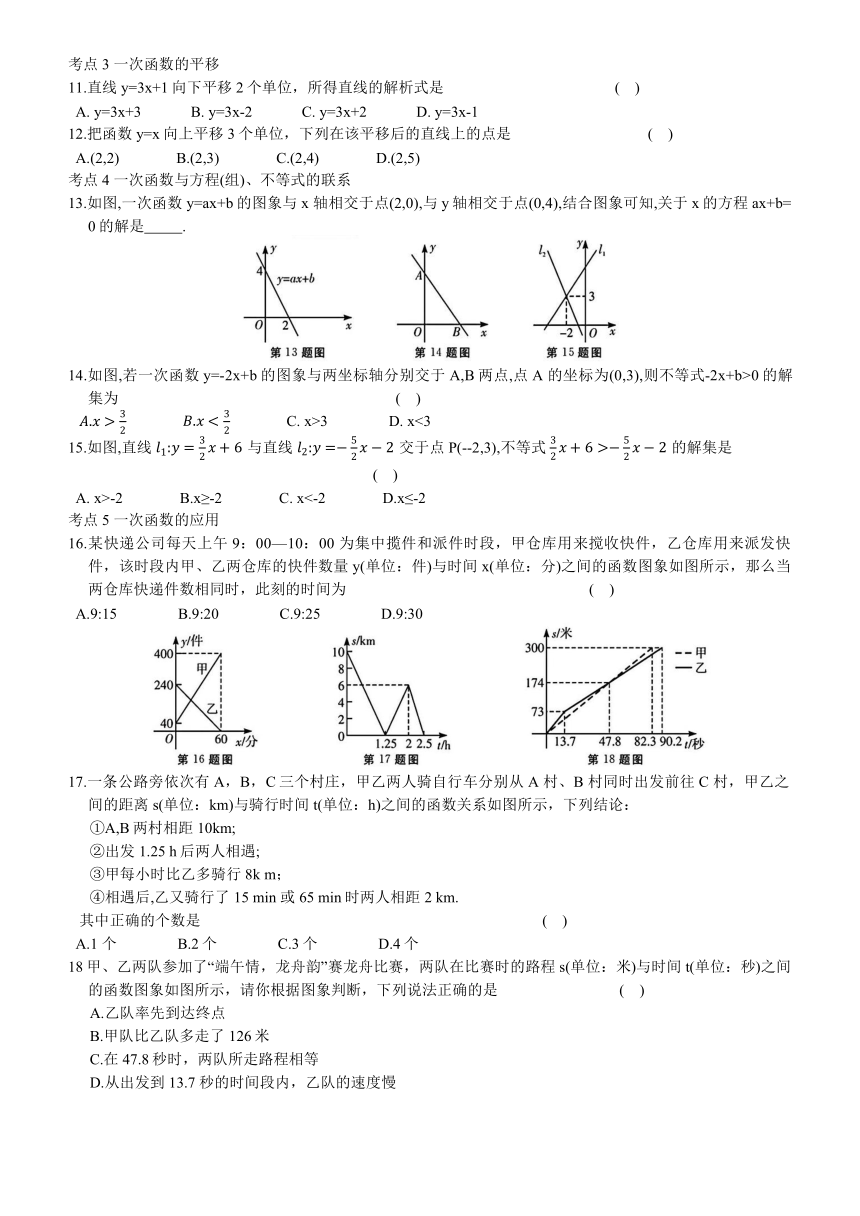
13.如图,一次函数y=ax+b的图象与x 轴相交于点(2,0),与y轴相交于点(0,4),结合图象可知,关于x的方程ax+b=0的解是 .
14.如图,若一次函数y=-2x+b的图象与两坐标轴分别交于A,B两点,点A 的坐标为(0,3),则不等式-2x+b>0的解集为 ( )
C. x>3 D. x<3
15.如图,直线 与直线 交于点 P(--2,3),不等式 的解集是 ( )
A. x>-2 B.x≥-2 C. x<-2 D.x≤-2
考点5 一次函数的应用
16.某快递公司每天上午9:00—10:00 为集中揽件和派件时段,甲仓库用来搅收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(单位:件)与时间x(单位:分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为 ( )
A.9:15 B.9:20 C.9:25 D.9:30
17.一条公路旁依次有A,B,C三个村庄,甲乙两人骑自行车分别从 A 村、B 村同时出发前往C 村,甲乙之间的距离s(单位:km)与骑行时间t(单位:h)之间的函数关系如图所示,下列结论:
①A,B两村相距10km;
②出发1.25 h后两人相遇;
③甲每小时比乙多骑行 8k m;
④相遇后,乙又骑行了 15 min 或65 min时两人相距2 km.
其中正确的个数是 ( )
A.1 个 B.2个 C.3个 D.4个
18甲、乙两队参加了“端午情,龙舟韵”赛龙舟比赛,两队在比赛时的路程s(单位:米)与时间t(单位:秒)之间的函数图象如图所示,请你根据图象判断,下列说法正确的是 ( )
A.乙队率先到达终点
B.甲队比乙队多走了 126米
C.在 47.8秒时,两队所走路程相等
D.从出发到13.7 秒的时间段内,乙队的速度慢
19.小王骑车从甲地到乙地,小李骑车从乙地到甲地,小王的速度小于小李的速度,两人同时出发,沿同一条公路匀速前进.图中的折线表示两人之间的距离y(单位:km)与小王的行驶时间x(单位:h)之间的函数关系.
请你根据图象进行探究:
(1)小王和小李的速度分别是多少
(2)求线段BC所表示的y与x之间的函数解析式,并写出自变量x的取值范围.
20.友谊商店A型号笔记本电脑的售价是a 元/台.最近,该商店对A 型号笔记本电脑举行促销活动,有两种优惠方案.方案一:每台按售价的九折销售;方案二:若购买不超过5台,每台按售价销售;若超过5台,超过的部分每台按售价的八折销售.某公司一次性从友谊商店购买 A型号笔记本电脑x 台.
(1)当 时,应选择哪种方案,该公司购买费用最少 最少费用是多少元
(2)若该公司采用方案二购买更合算,求x的取值范围.
21.根据记录,从地面向上11 km以内,每升高1km,气温降低 ;又知在距离地面11 km以上高空,气温几乎不变.若地面气温为m(单位: ,设距地面的高度为x(单位:km)处的气温为y(单位:
(1)写出距地面的高度在11 km以内的y与x之间的函数表达式;
(2)上周日,小敏在乘飞机从上海飞回西安途中,某一时刻,她从机舱内屏幕显示的相关数据得知,飞机外气温为 时,飞机距离地面的高度为7km,求当时这架飞机下方地面的气温;小敏想,假如飞机当时在距离地面 12km的高空,飞机外的气温是多少度呢 请求出假如当时飞机距离地面12km时,飞机外的气温.
22.有A,B两个发电厂,每焚烧1 吨垃圾,A 发电厂比B 发电厂多发 40度电,A 焚烧20吨垃圾比 B焚烧30 吨垃圾少1800度电.
(1)求焚烧 1 吨垃圾,A 和B 各发电多少度
(2)A,B两个发电厂共焚烧90吨的垃圾,A 焚烧的垃圾不多于B 焚烧的垃圾两倍,求 A 厂和B 厂总发电量的最大值.
23.甲、乙两地间的直线公路长为400千米.一辆轿车和一辆货车分别沿该公路从甲、乙两地以各自的速度匀速相向而行,货车比轿车早出发1小时,途中轿车出现了故障,停下维修,货车仍继续行驶.1小时后轿车故障被排除,此时接到通知,轿车立刻掉头按原路原速返回甲地(接到通知及掉头时间不计).最后两车同时到达甲地,已知两车距各自出发地的距离y(单位:千米)与轿车所用的时间x(单位:小时)的关系如图所示,请结合图象解答下列问题:
(1)货车的速度是 千米/小时;轿车的速度是 千米/小时;t值为 .
(2)求轿车距其出发地的距离y(单位:千米)与所用时间x(单位:小时)之间的函数关系式并写出自变量x的取值范围;
(3)请直接写出货车出发多长时间两车相距90千米.
章末整合·感知中考
【中考完全接触】
1. D 2. A 3. D 4. D 5. A 6. D 7. D 8. A 9. B
10.解:(1)k=-2时,
根据题意,得
-2x+2>x-3.
解得
(2)当x=1时,y=x-3=--2,把(1,-2)代入 y =kx+2 得k+2=-2,解得k=-4.
当--4≤k<0时,y >y ;
当0所以k的范围为-4≤k≤1且k≠0.
11. D 12. D 13. x=2 14. B 15. A 16. B17. D 18. C19.解:(1)由图可得,
小王的速度为:30÷3=10 km/h,
小李的速度为:(30-10×1)÷1=20km/h.
答:小王和小李的速度分别是10km/h、20 km/h.
(2)小李从乙地到甲地用的时间为1.5h,
当小李到达甲地时,两人之间的距离为:10×1.5=15 km,
∴点C的坐标为(1.5,15).
设线段BC所表示的y与x 之间的函数解析式为y=kx+b,
得
即线段BC所表示的y与x 之间的函数解析式是y=30x-30(1≤x≤1.5).
20.解:设购买A型号笔记本电脑x台时的费用为ω元,(1)当x=8时,
方案一:w=90%a×8=7.2a,
方案二:w=5a+(8-5)a×80%=7.4a,
∴当x=8时,应选择方案一,该公司购买费用最少,最少费用是7.2a元.
(2)∵若该公司采用方案二购买更合算,∴x>5.
方案一:w=90%ax=0.9ax.
方案二:当x>5时,w=5a+(x-5)a×80%=5a+0.8ax--4a=a+0.8ax,
则 0.9ax>a+0.8ax,
x>10.
∴x的取值范围是x>10.
21.解:(1)根据题意,得y=m-6x.
(2)将x=7,y=-26代入y=m-6x,得-26=m-42,∴m=16.
∴当时地面气温为 16 ℃.
∵x=12>11,
∴y=16-6×11=-50(℃).
假如当时飞机距地面12 km时,飞机外的气温为一50℃.
22.解:(1)设焚烧1吨垃圾,A 发电厂发电a 度,B 发电厂发电b度,根据题意,得
解得
答:焚烧1吨垃圾,A 发电厂发电 300度,B发电厂发电 260 度.
(2)设 A 发电厂焚烧x 吨垃圾,则 B 发电厂焚烧(90-x)吨垃圾,总发电量为y度,则
y=300x+260(90-x)=40x+23 400,
∵x≤2(90-x),∴x≤60.
∵y随x的增大而增大,
∴当x=60时,y有最大值为:40×60+23 400=25 800(度).
答:A厂和B厂总发电量的最大是25 800度.
23.解:(1)货车的速度是 50 千米/时;轿车的速度是:480÷(7-1)=80千米/时;t=240÷80=3.
故答案为:50;80;3.
(2)由题意可知:A(3,240),B(4,240),C(7,0),设直线OA的解析式为 ∴y=80x(0≤x<3).
当3≤x<4时,y=240,
设直线 BC的解析式为 把 B(4,240),C(7,0)代入,得
解得(k =-80.0)∴y=-80x+560.
).
(3)设货车出发x小时后两车相距90千米,根据题意,得
50x+80(x--1)=400-90或50x+80(x-2)=400+90.
解得x=3或5.
答:货车出发3 小时或5 小时后两车相距90千米.
函数名称 解析式 性质
正比例函数 y=kx(k≠0) ①k>0,图象在第一、三象限,y随x 的增大而增大;②k<0,图象在第二、四象限,y随x的增大而减小
一次函数 y=kx+b(k≠0) ①k>0,y随x的增大而增大; ②k<0,y随x的增大而减小
k,b的符号 k>0,b>0 k>0,b<0 k<0,b>0 k<0,b<0
一次函数图象的大致位置
9.待定系数法:先设出函数解析式,再根据条件确定解析式中未知的系数,从而得出函数解析式的方法,叫做待定系数法.
待定系数法求一次函数解析式的步骤:
(1)设:先设出一次函数的解析式为y=kx+b(k≠0);
(2)代:将已知条件代入解析式中,建立方程或方程组;
(3)解:解方程或方程组,确定未知系数的值;
(4)写:写出解析式.
10.分段函数的应用,要特别注意自变量取值范围的划分,既要科学合理,又要符合实际.
11.一元一次方程kx+b=0的解,是一次函数y=kx+b与x轴交点( 的横坐标,即
12.求一元一次不等式ax+b>0或ax+b<0(a,b为常数,a≠0)的解,相当于一次函数y=ax+b的函数值y>0或y<0时,求自变量的取值范围,也相当于这个函数图象在x轴上方或下方时,找对应的x的取值范围.
13.两条直线的交点坐标 两解析式组成的方程组的解.
中考完全接触
考点 1 函数自变量的取值范围
1.函数 中, 自变量x的取值范围是 ( )
且x≠-1 且x≠-1
2.函数 中自变量 x的取值范围是 ( )
A.x≥-2且x≠1 B.x≥-2 C. x≠1 D.-2≤x<1
考点 2 一次函数的图象与性质
3.在平面直角坐标系中,函数y=kx+b的图象如图所示,则下列判断正确的是 ( )
A. k>0
B. b<0
C. k·b>0
D. k·b<0
4.下列关于一次函数.y=kx+b(k<0,b>0)的说法,错误的是
A.图象经过第一、二、四象限 B. y随x的增大而减小
C.图象与 y轴交于点(0,b) D.当 时,y>0
5.如图,直线 与直线 交于点 P(-2,3),不等式 的解集是 ( )
A. x>-2
B.x≥-2
C. x<-2
D.x≤-2
6.若一次函数y=kx+b(k,b为常数,且k≠0)的图象经过点 A(0,-1),B(1,1),则不等式kx+b>1的解为
A. x<0 B. x>0 C. x<1 D. x>1
7.已知A,B两地相距3千米,小黄从 A 地到 B 地,平均速度为4 千米/时,若用x 表示行走的时间(单位:小时),y表示余下的路程(单位:千米),则y关于x 的函数解析式是 ( )
A. y=4x(x≥0)
C. y=3-4x(x≥0)
8.一个装有进水管和出水管的空容器,从某时刻开始4m in内只进水不出水,容器内存水 8L;在随后的8min内既进水又出水,容器内存水12 L;接着关闭进水管直到容器内的水放完.若每分钟进水量和出水量是两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的函数关系的图象大致的是 ( )
9.如图,点 P是菱形ABCD 边上的一动点,它从点 A 出发沿在A→B→C→D路径匀速运动到点 D,设 的面积为y,P 点的运动时间为x,则y关于x的函数图象大致为 ( )
10.已知一次函数 (k为常数,k≠0)和
(1)当. 时,若 ,求x的取值范围;
(2)当x<1时, 结合图象,直接写出k的取值范围.
考点3 一次函数的平移
11.直线y=3x+1向下平移2个单位,所得直线的解析式是 ( )
A. y=3x+3 B. y=3x-2 C. y=3x+2 D. y=3x-1
12.把函数y=x向上平移3个单位,下列在该平移后的直线上的点是 ( )
A.(2,2) B.(2,3) C.(2,4) D.(2,5)
考点 4 一次函数与方程(组)、不等式的联系
13.如图,一次函数y=ax+b的图象与x 轴相交于点(2,0),与y轴相交于点(0,4),结合图象可知,关于x的方程ax+b=0的解是 .
14.如图,若一次函数y=-2x+b的图象与两坐标轴分别交于A,B两点,点A 的坐标为(0,3),则不等式-2x+b>0的解集为 ( )
C. x>3 D. x<3
15.如图,直线 与直线 交于点 P(--2,3),不等式 的解集是 ( )
A. x>-2 B.x≥-2 C. x<-2 D.x≤-2
考点5 一次函数的应用
16.某快递公司每天上午9:00—10:00 为集中揽件和派件时段,甲仓库用来搅收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(单位:件)与时间x(单位:分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为 ( )
A.9:15 B.9:20 C.9:25 D.9:30
17.一条公路旁依次有A,B,C三个村庄,甲乙两人骑自行车分别从 A 村、B 村同时出发前往C 村,甲乙之间的距离s(单位:km)与骑行时间t(单位:h)之间的函数关系如图所示,下列结论:
①A,B两村相距10km;
②出发1.25 h后两人相遇;
③甲每小时比乙多骑行 8k m;
④相遇后,乙又骑行了 15 min 或65 min时两人相距2 km.
其中正确的个数是 ( )
A.1 个 B.2个 C.3个 D.4个
18甲、乙两队参加了“端午情,龙舟韵”赛龙舟比赛,两队在比赛时的路程s(单位:米)与时间t(单位:秒)之间的函数图象如图所示,请你根据图象判断,下列说法正确的是 ( )
A.乙队率先到达终点
B.甲队比乙队多走了 126米
C.在 47.8秒时,两队所走路程相等
D.从出发到13.7 秒的时间段内,乙队的速度慢
19.小王骑车从甲地到乙地,小李骑车从乙地到甲地,小王的速度小于小李的速度,两人同时出发,沿同一条公路匀速前进.图中的折线表示两人之间的距离y(单位:km)与小王的行驶时间x(单位:h)之间的函数关系.
请你根据图象进行探究:
(1)小王和小李的速度分别是多少
(2)求线段BC所表示的y与x之间的函数解析式,并写出自变量x的取值范围.
20.友谊商店A型号笔记本电脑的售价是a 元/台.最近,该商店对A 型号笔记本电脑举行促销活动,有两种优惠方案.方案一:每台按售价的九折销售;方案二:若购买不超过5台,每台按售价销售;若超过5台,超过的部分每台按售价的八折销售.某公司一次性从友谊商店购买 A型号笔记本电脑x 台.
(1)当 时,应选择哪种方案,该公司购买费用最少 最少费用是多少元
(2)若该公司采用方案二购买更合算,求x的取值范围.
21.根据记录,从地面向上11 km以内,每升高1km,气温降低 ;又知在距离地面11 km以上高空,气温几乎不变.若地面气温为m(单位: ,设距地面的高度为x(单位:km)处的气温为y(单位:
(1)写出距地面的高度在11 km以内的y与x之间的函数表达式;
(2)上周日,小敏在乘飞机从上海飞回西安途中,某一时刻,她从机舱内屏幕显示的相关数据得知,飞机外气温为 时,飞机距离地面的高度为7km,求当时这架飞机下方地面的气温;小敏想,假如飞机当时在距离地面 12km的高空,飞机外的气温是多少度呢 请求出假如当时飞机距离地面12km时,飞机外的气温.
22.有A,B两个发电厂,每焚烧1 吨垃圾,A 发电厂比B 发电厂多发 40度电,A 焚烧20吨垃圾比 B焚烧30 吨垃圾少1800度电.
(1)求焚烧 1 吨垃圾,A 和B 各发电多少度
(2)A,B两个发电厂共焚烧90吨的垃圾,A 焚烧的垃圾不多于B 焚烧的垃圾两倍,求 A 厂和B 厂总发电量的最大值.
23.甲、乙两地间的直线公路长为400千米.一辆轿车和一辆货车分别沿该公路从甲、乙两地以各自的速度匀速相向而行,货车比轿车早出发1小时,途中轿车出现了故障,停下维修,货车仍继续行驶.1小时后轿车故障被排除,此时接到通知,轿车立刻掉头按原路原速返回甲地(接到通知及掉头时间不计).最后两车同时到达甲地,已知两车距各自出发地的距离y(单位:千米)与轿车所用的时间x(单位:小时)的关系如图所示,请结合图象解答下列问题:
(1)货车的速度是 千米/小时;轿车的速度是 千米/小时;t值为 .
(2)求轿车距其出发地的距离y(单位:千米)与所用时间x(单位:小时)之间的函数关系式并写出自变量x的取值范围;
(3)请直接写出货车出发多长时间两车相距90千米.
章末整合·感知中考
【中考完全接触】
1. D 2. A 3. D 4. D 5. A 6. D 7. D 8. A 9. B
10.解:(1)k=-2时,
根据题意,得
-2x+2>x-3.
解得
(2)当x=1时,y=x-3=--2,把(1,-2)代入 y =kx+2 得k+2=-2,解得k=-4.
当--4≤k<0时,y >y ;
当0
11. D 12. D 13. x=2 14. B 15. A 16. B17. D 18. C19.解:(1)由图可得,
小王的速度为:30÷3=10 km/h,
小李的速度为:(30-10×1)÷1=20km/h.
答:小王和小李的速度分别是10km/h、20 km/h.
(2)小李从乙地到甲地用的时间为1.5h,
当小李到达甲地时,两人之间的距离为:10×1.5=15 km,
∴点C的坐标为(1.5,15).
设线段BC所表示的y与x 之间的函数解析式为y=kx+b,
得
即线段BC所表示的y与x 之间的函数解析式是y=30x-30(1≤x≤1.5).
20.解:设购买A型号笔记本电脑x台时的费用为ω元,(1)当x=8时,
方案一:w=90%a×8=7.2a,
方案二:w=5a+(8-5)a×80%=7.4a,
∴当x=8时,应选择方案一,该公司购买费用最少,最少费用是7.2a元.
(2)∵若该公司采用方案二购买更合算,∴x>5.
方案一:w=90%ax=0.9ax.
方案二:当x>5时,w=5a+(x-5)a×80%=5a+0.8ax--4a=a+0.8ax,
则 0.9ax>a+0.8ax,
x>10.
∴x的取值范围是x>10.
21.解:(1)根据题意,得y=m-6x.
(2)将x=7,y=-26代入y=m-6x,得-26=m-42,∴m=16.
∴当时地面气温为 16 ℃.
∵x=12>11,
∴y=16-6×11=-50(℃).
假如当时飞机距地面12 km时,飞机外的气温为一50℃.
22.解:(1)设焚烧1吨垃圾,A 发电厂发电a 度,B 发电厂发电b度,根据题意,得
解得
答:焚烧1吨垃圾,A 发电厂发电 300度,B发电厂发电 260 度.
(2)设 A 发电厂焚烧x 吨垃圾,则 B 发电厂焚烧(90-x)吨垃圾,总发电量为y度,则
y=300x+260(90-x)=40x+23 400,
∵x≤2(90-x),∴x≤60.
∵y随x的增大而增大,
∴当x=60时,y有最大值为:40×60+23 400=25 800(度).
答:A厂和B厂总发电量的最大是25 800度.
23.解:(1)货车的速度是 50 千米/时;轿车的速度是:480÷(7-1)=80千米/时;t=240÷80=3.
故答案为:50;80;3.
(2)由题意可知:A(3,240),B(4,240),C(7,0),设直线OA的解析式为 ∴y=80x(0≤x<3).
当3≤x<4时,y=240,
设直线 BC的解析式为 把 B(4,240),C(7,0)代入,得
解得(k =-80.0)∴y=-80x+560.
).
(3)设货车出发x小时后两车相距90千米,根据题意,得
50x+80(x--1)=400-90或50x+80(x-2)=400+90.
解得x=3或5.
答:货车出发3 小时或5 小时后两车相距90千米.
