初中数学人教版八年级下册 19.2.2一次函数的概念同步练习(第 2课时)
文档属性
| 名称 | 初中数学人教版八年级下册 19.2.2一次函数的概念同步练习(第 2课时) |  | |
| 格式 | docx | ||
| 文件大小 | 104.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-03 17:15:19 | ||
图片预览


文档简介
第 2课时 一次函数的概念
基础知识夯实
知识沉淀
1.一次函数的定义:一般地,形如 (k,b是常数,k 0)的函数,叫做一次函数.
2.一次函数与正比例函数:对于一次函数y=kx+b(k,b是常数,k≠0),当b=0时,y=kx+b,即 ,所以说正比例函数是一种特殊的一次函数.
3.一般情况下,一次函数的自变量的取值范围是 ,在实际问题中,受实际情况限制可能取不到全体实数.
基础过关
1.下列函数的解析式中是一次函数的是 ( )
2.已知函数.y=(m--1)x|m|+3是一次函数,则m=
典型案例探究
知识点1 一次函数的概念
【例题1】下列函数中, 是一次函数, 是正比例函数.(填序号)
①y=8x;②y=二 ;③y=-5x +6;④y=4--3x;
⑤y=0.5x--1;⑥y=2(x--3).
【例题2】已知 是一次函数.
(1)求k的值;
(2)若点(2,a)在这个一次函数的图象上,求 a的值.
【变式1】下列函数中,是一次函数的有 ( )
①y=3x+1;②y=1--3x; ③y= ; ④y=-2x;
A.4个 B.3个
C.2个 D.1个
【变式2】已知函数
(1)当m为何值时,y是x 的一次函数;
(2)若函数是一次函数,则x为何值时,y的值为3.知识点 2 实际问题中的一次函数模型
【例题3】长方形相邻两边的长分别是6 cm,x cm.
(1)写出长方形的周长 y cm 和边 x cm 的函数关系式;
(2)求当x=5cm时长方形的周长y的值;
(3)写出自变量x的取值范围.
【变式 3】已知等腰三角形周长为 20.
(1)写出底边 y关于腰长x的函数解析式;
(2)写出自变量x的取值范围.
课后作业
A 组
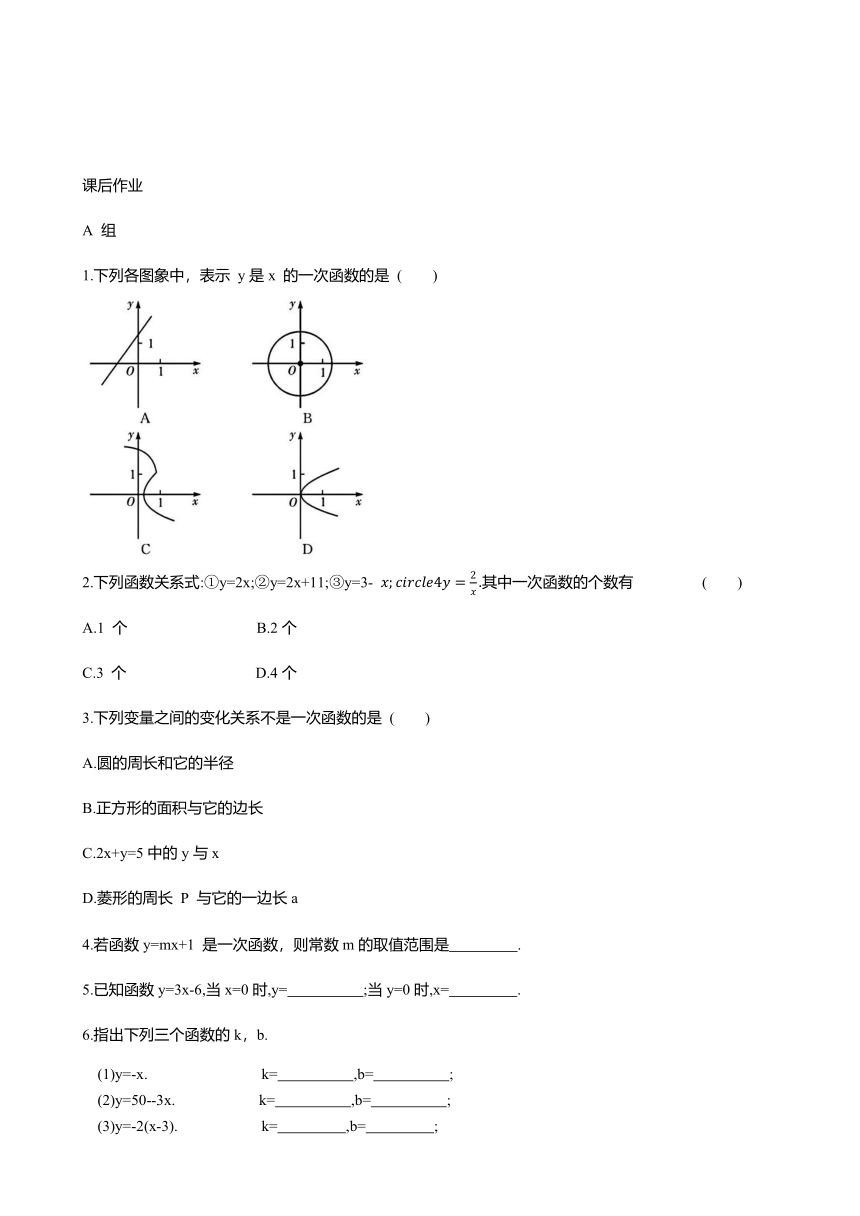
1.下列各图象中,表示 y是x 的一次函数的是 ( )
2.下列函数关系式:①y=2x;②y=2x+11;③y=3- 其中一次函数的个数有 ( )
A.1 个 B.2个
C.3 个 D.4个
3.下列变量之间的变化关系不是一次函数的是 ( )
A.圆的周长和它的半径
B.正方形的面积与它的边长
C.2x+y=5中的y与x
D.菱形的周长 P 与它的一边长a
4.若函数y=mx+1 是一次函数,则常数m的取值范围是 .
5.已知函数y=3x-6,当x=0时,y= ;当y=0时,x= .
6.指出下列三个函数的k,b.
(1)y=-x. k= ,b= ;
(2)y=50--3x. k= ,b= ;
(3)y=-2(x-3). k= ,b= ;
k= ,b= .
7.已知一次函数 y=2x-3.
(1)当x=-2时,求y;
(2)当y=1时,求x;
(3)当-3B 组
8.已知
(1)当m,n取何值时,y是x 的一次函数
(2)当m,n取何值时,y是x的正比例函数
9.某种气体在( 时的体积为 100 L,温度每升高 它的体积增加0.37 L.
(1)写出气体体积V(单位:L)与温度t(单位:℃)之间的函数解析式;
(2)求当温度为 时气体的体积;
(3)气体的体积为107.4 L时,温度为多少摄氏度
C组
已知函数 当k取何值时,y是x的一次函数
第2 课时 一次函数的概念
【基础知识夯实】
知识沉淀
1. y=kx+b ≠ 2. y=kx 3.全体实数
基础过关
1. B 2.-1
【典型案例探究】
例题1 ①④⑤⑥ ①
变式1 B
例题2解:(1)∵y是一次函数,
∴|k|=1.解得k=±1.
又∵k-1≠0,∴k≠1.∴k=-1.
(2)将k=-1代入得一次函数的解析式为
y=-2x+1.
∵(2,a)在y=-2x+1图象上,
∴a=-4+1=-3.
变式2解:(1)由.是一次函数,得 解得m=-2.
故当m=-2时,是一次函数.
(2)由(1),得y=-4x+5.
当y=3时,3=-4x+5,解得
故当 时,y的值为3.
例题3(1)y=12+2x (2)22cm (3)x>0
变式3 (1)y=20-2x (2)5【课后作业】
1. A 2. C 3. B 4. m≠0 5.-6 2
6.(1)-1 0 (2)-3 50 (3)-2 6
7.解:(1)把x=-2代入y=2x-3中,得y=-4-3=-7.
(2)把y=1代入y=2x-3中,得1=2x-3.
解得x=2.
(3)∵-3解得
8.解:(1)根据一次函数的定义得2--|m|=1,解得 m=±1.
又∵m--1≠0,即m≠1,
∴当m=-1,n为任意实数时,这个函数是一次函数.
(2)根据正比例函数的定义得2--|m|=1,n+3=0,解得m=±1,n=-3.
又∵m-1≠0,即 m≠1,
∴当m=-1,n=-3时,这个函数是正比例函数.
9.解:(1)V=0.37t+100.
(2)V=111.1 L.
(3)20℃.
10.当 或±1时,y是x的一次函数.
基础知识夯实
知识沉淀
1.一次函数的定义:一般地,形如 (k,b是常数,k 0)的函数,叫做一次函数.
2.一次函数与正比例函数:对于一次函数y=kx+b(k,b是常数,k≠0),当b=0时,y=kx+b,即 ,所以说正比例函数是一种特殊的一次函数.
3.一般情况下,一次函数的自变量的取值范围是 ,在实际问题中,受实际情况限制可能取不到全体实数.
基础过关
1.下列函数的解析式中是一次函数的是 ( )
2.已知函数.y=(m--1)x|m|+3是一次函数,则m=
典型案例探究
知识点1 一次函数的概念
【例题1】下列函数中, 是一次函数, 是正比例函数.(填序号)
①y=8x;②y=二 ;③y=-5x +6;④y=4--3x;
⑤y=0.5x--1;⑥y=2(x--3).
【例题2】已知 是一次函数.
(1)求k的值;
(2)若点(2,a)在这个一次函数的图象上,求 a的值.
【变式1】下列函数中,是一次函数的有 ( )
①y=3x+1;②y=1--3x; ③y= ; ④y=-2x;
A.4个 B.3个
C.2个 D.1个
【变式2】已知函数
(1)当m为何值时,y是x 的一次函数;
(2)若函数是一次函数,则x为何值时,y的值为3.知识点 2 实际问题中的一次函数模型
【例题3】长方形相邻两边的长分别是6 cm,x cm.
(1)写出长方形的周长 y cm 和边 x cm 的函数关系式;
(2)求当x=5cm时长方形的周长y的值;
(3)写出自变量x的取值范围.
【变式 3】已知等腰三角形周长为 20.
(1)写出底边 y关于腰长x的函数解析式;
(2)写出自变量x的取值范围.
课后作业
A 组
1.下列各图象中,表示 y是x 的一次函数的是 ( )
2.下列函数关系式:①y=2x;②y=2x+11;③y=3- 其中一次函数的个数有 ( )
A.1 个 B.2个
C.3 个 D.4个
3.下列变量之间的变化关系不是一次函数的是 ( )
A.圆的周长和它的半径
B.正方形的面积与它的边长
C.2x+y=5中的y与x
D.菱形的周长 P 与它的一边长a
4.若函数y=mx+1 是一次函数,则常数m的取值范围是 .
5.已知函数y=3x-6,当x=0时,y= ;当y=0时,x= .
6.指出下列三个函数的k,b.
(1)y=-x. k= ,b= ;
(2)y=50--3x. k= ,b= ;
(3)y=-2(x-3). k= ,b= ;
k= ,b= .
7.已知一次函数 y=2x-3.
(1)当x=-2时,求y;
(2)当y=1时,求x;
(3)当-3
8.已知
(1)当m,n取何值时,y是x 的一次函数
(2)当m,n取何值时,y是x的正比例函数
9.某种气体在( 时的体积为 100 L,温度每升高 它的体积增加0.37 L.
(1)写出气体体积V(单位:L)与温度t(单位:℃)之间的函数解析式;
(2)求当温度为 时气体的体积;
(3)气体的体积为107.4 L时,温度为多少摄氏度
C组
已知函数 当k取何值时,y是x的一次函数
第2 课时 一次函数的概念
【基础知识夯实】
知识沉淀
1. y=kx+b ≠ 2. y=kx 3.全体实数
基础过关
1. B 2.-1
【典型案例探究】
例题1 ①④⑤⑥ ①
变式1 B
例题2解:(1)∵y是一次函数,
∴|k|=1.解得k=±1.
又∵k-1≠0,∴k≠1.∴k=-1.
(2)将k=-1代入得一次函数的解析式为
y=-2x+1.
∵(2,a)在y=-2x+1图象上,
∴a=-4+1=-3.
变式2解:(1)由.是一次函数,得 解得m=-2.
故当m=-2时,是一次函数.
(2)由(1),得y=-4x+5.
当y=3时,3=-4x+5,解得
故当 时,y的值为3.
例题3(1)y=12+2x (2)22cm (3)x>0
变式3 (1)y=20-2x (2)5
1. A 2. C 3. B 4. m≠0 5.-6 2
6.(1)-1 0 (2)-3 50 (3)-2 6
7.解:(1)把x=-2代入y=2x-3中,得y=-4-3=-7.
(2)把y=1代入y=2x-3中,得1=2x-3.
解得x=2.
(3)∵-3
8.解:(1)根据一次函数的定义得2--|m|=1,解得 m=±1.
又∵m--1≠0,即m≠1,
∴当m=-1,n为任意实数时,这个函数是一次函数.
(2)根据正比例函数的定义得2--|m|=1,n+3=0,解得m=±1,n=-3.
又∵m-1≠0,即 m≠1,
∴当m=-1,n=-3时,这个函数是正比例函数.
9.解:(1)V=0.37t+100.
(2)V=111.1 L.
(3)20℃.
10.当 或±1时,y是x的一次函数.
