初中数学人教版八年级下册19.1.2 函数的图象同步练习(第2课时)(含答案)
文档属性
| 名称 | 初中数学人教版八年级下册19.1.2 函数的图象同步练习(第2课时)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 704.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-03 17:24:44 | ||
图片预览


文档简介
第十九章 一次函数
第 2 课时 函数的图象
基础知识夯实
知识沉淀
1.描点法画函数图象的一般步骤:
(1) ;
(2) ;
(3) .
2.函数的三种表示方法:
(1) 法;
(2)列表法;
(3)图象法.
基础过关
1.下列图象中,y不是x 的函数的是 ( )
2.小高从家门口骑车去单位上班,先走平路到达点A,再走上坡路到达点B,最后走下坡路到达工作单位,所用的时间与路程的关系如图所示.下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上班时一致,那么他从单位到家门口需要的时间是 分钟.
典型案例探究
知识点1根据图象分析相关信息
【例题1】如图反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家.其中x表示时间,y 表示张强离家的距离.根据图象回答下列问题:(1)体育场离张强家 km,张强从家到体育馆用了 min;
(2)体育场离文具店 km,张强在文具店停留了 min;
(3)请计算:张强从文具店回家的平均速度是多少
【变式1】如图表示的是热带风暴从发生到结束的全过程.请结合图象回答下列问题:
(1)热带风暴从开始发生到结束共经历了 小时;
(2)从图象上看,风速在 (单位:小时)时间段内增大的最快,最大风速是 千米/时;
(3)风速从开始减小到最终停止,平均每小时减小多少千米
知识点 2 函数图象的画法
【例题2】某校办工厂,现在年产值是 15万元,计划今后每年增加2万元.
(1)写出年产值y(单位:万元)与年数x之间的函数关系式;
(2)画出函数图象;
(3)求5年后的年产值.
【变式2】在如图所示的平面直角坐标系中画出函数 的图象.
x
y
知识点 3 函数的三种表示方法
【例题3】已知等腰三角形的周长为12 cm,若底边长为y cm,一腰长为 x cm.
(1)确定y与x之间的函数关系式;
(2)确定x的取值范围;
(3)画出函数的图象.
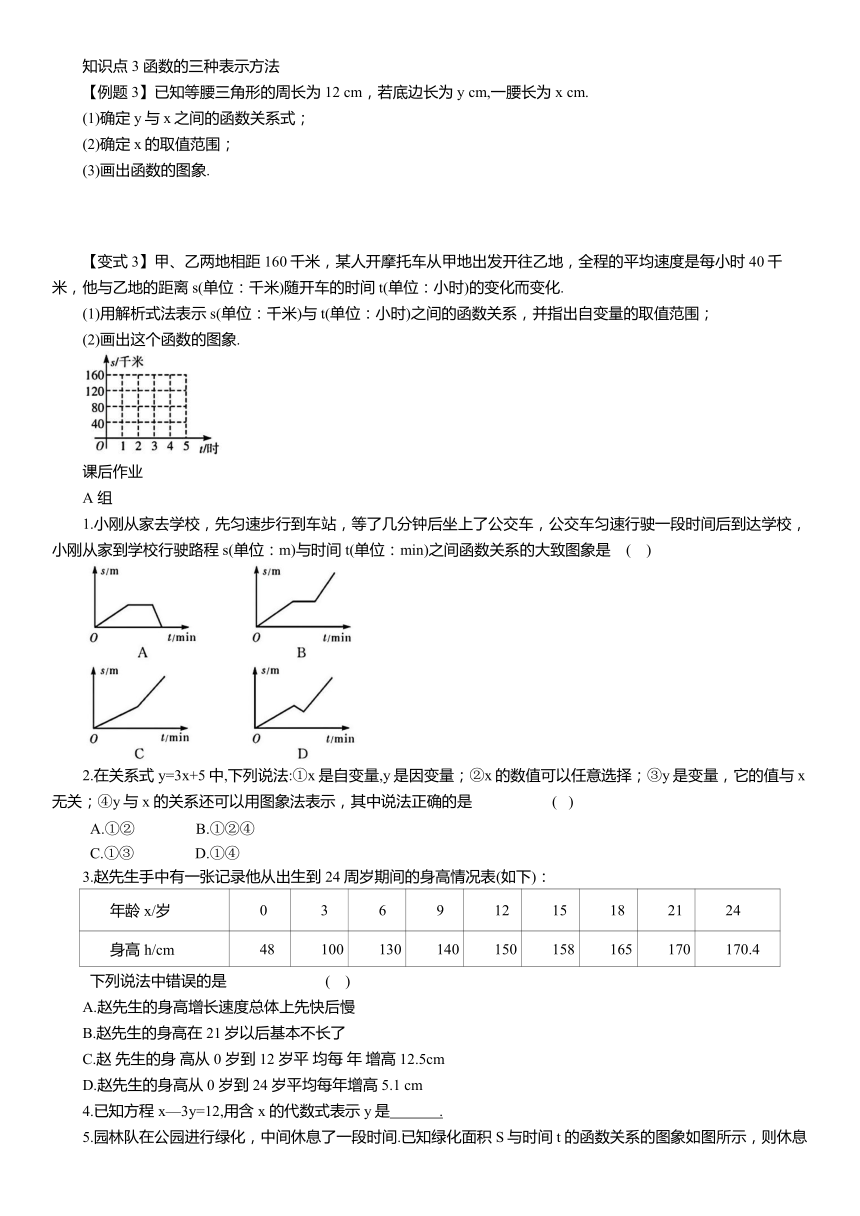
【变式3】甲、乙两地相距160千米,某人开摩托车从甲地出发开往乙地,全程的平均速度是每小时 40千米,他与乙地的距离s(单位:千米)随开车的时间t(单位:小时)的变化而变化.
(1)用解析式法表示 s(单位:千米)与t(单位:小时)之间的函数关系,并指出自变量的取值范围;
(2)画出这个函数的图象.
课后作业
A 组
1.小刚从家去学校,先匀速步行到车站,等了几分钟后坐上了公交车,公交车匀速行驶一段时间后到达学校,小刚从家到学校行驶路程s(单位:m)与时间 t(单位:min)之间函数关系的大致图象是 ( )
2.在关系式 y=3x+5中,下列说法:①x是自变量,y是因变量;②x的数值可以任意选择;③y是变量,它的值与x无关;④y与x 的关系还可以用图象法表示,其中说法正确的是 ( )
A.①② B.①②④
C.①③ D.①④
3.赵先生手中有一张记录他从出生到 24 周岁期间的身高情况表(如下):
年龄x/岁 0 3 6 9 12 15 18 21 24
身高 h/cm 48 100 130 140 150 158 165 170 170.4
下列说法中错误的是 ( )
A.赵先生的身高增长速度总体上先快后慢
B.赵先生的身高在21岁以后基本不长了
C.赵 先生的身 高从 0 岁到 12 岁平 均每 年 增高12.5cm
D.赵先生的身高从 0 岁到 24 岁平均每年增高5.1 cm
4.已知方程 x—3y=12,用含 x 的代数式表示 y是 .
5.园林队在公园进行绿化,中间休息了一段时间.已知绿化面积S与时间t 的函数关系的图象如图所示,则休息后园林队绿化面积为 平方米.
6.某次大型活动,组委会启用无人机航拍活动过程,在操控无人机时应根据现场状况调节高度,已知无人机在上升和下降过程中速度相同,设无人机的飞行高度h(单位:米)与操控无人机的时间t(单位:分钟)之间的关系如图中的实线所示,根据图象回答下列问题:
(1)图中的自变量是 ,因变量是 ;
(2)无人机在75米高的上空停留的时间是 分钟;
(3)在上升或下降过程中,无人机的速度为 米/分;
(4)图中a表示的数是 ;b表示的数是 ;
(5)图中点 A 表示 ·
B 组
7.父亲告诉小明:“距离地面越远,温度越低,”并给小明出示了下面的表格.
距离地面高度/千米 0 1 2 3 4 5
温度/℃ 20 14 8 2 -4 -10
根据上表,父亲还给小明出了下面几个问题,你和小明一起回答.
(1)上表反映了哪两个变量之间的关系 哪个是自变量 哪个是因变量
(2)如果用h表示距离地面的高度,用t 表示温度,那么随着h的变化,t是怎么变化的
(3)你知道距离地面5千米的高空温度是多少吗
(4)你能猜出距离地面6 千米的高空温度是多少吗
8.某天,小颖到校后发现有学习用品遗忘在家中,此时离上课还有15分钟,于是立即步行回家去取.同时小颖的爸爸从家中出发骑自行车给她送学习用品,两人在途中相遇,在这个过程中,小颖和爸爸两人离学校的距离s(单位:m)与所用时间t(单位:min)之间的关系如图所示,若爸爸骑自行车的速度是小颖步行的4倍,根据图中提供的信息,回答下列问题:
(1)学校离家的距离是 米,爸爸出发 分钟后与小颖相遇;
(2)请求出小颖步行的速度;
(3)若小颖与爸爸相遇后坐爸爸的自行车赶回学校(假设爸爸骑自行车的速度不变)小颖能在上课前到达学校吗 请说明理由.
C 组
9.函数可揭示事物变化规律,它有多种表示形式.如表格、图象、表达式等,这些表示形式各有优势.图象法直观、列表法具体、表达式精确.若把三者结合起来,则能更全面深刻地理解变量之间的关系.试解决下列问题.
(1)已知函数表达式 你能说出它的图象具有的一些特征吗 试画出它的图象;
(2)试说明下列函数的图象与 的图象之间的位置关系,并在同一平面直角坐标系中画出它们的图象.
第 2课时 函数的图象
【基础知识夯实】
知识沉淀
1.(1)列表 (2)描点 (3)连线
2.(1)解析式
基础过关
1. A 2.15
【典型案例探究】
例题1 (1)2.5 15 (2)1 20 (3) / km/min
变式1 解:(1)16.
由图象可得,热带风暴从开始发生到结束共经历了16 个小时.
(2)2~5 54
从图象上看,风速在2~5(小时)时间段内增大的最快,最大风速是 54 千米/时.
(3)风速从开始减小到最终停止,平均每小时减小:54÷(16-10)=54÷6=9(千米/时),即风速从开始减小到最终停止,平均每小时减小9千米/时.
例题2解:(1)函数关系式为y=15+2x(x≥0).
(2)列表:
x 0 1 2 3 4 5 6 ··
y=15+2x| 15 17 19 21 23 25 27
描点,连线,得出函数图象,如图.
变式2 略
例题3 解:(1)依题意,得 y=12-2x.
解得3∴自变量x的取值范围是3(3)列表:
x 3 4 5 5.5 6
y 6 4 2 1 0
描点,连线.其图象如图.
变式3 解:(1)s=160-40t,0≤1≤4.
(2)图象略.
【课后作业】
1. B 2. B 3. C 4. y= x--4 5.100
6.解:(1)自变量是时间(或t),因变量是高度(或h).
(2)5 (3)25 (4)2 15
(5)图中点 A 表示在第6 分钟时,无人机的飞行高度为50 米.
7.解:(1)上表反映了温度和距地面高度之间的关系,高度是自变量,温度是因变量.
(2)由表可知,每上升1千米,温度降低6摄氏度,可得解析式为t=20-6h.
(3)由表可知,距地面5千米时,温度为零下 10摄氏度.
(4)将t=6代入h=20-6t,可得t=20-6×6=-16.
8.解:(1)2 500 10
(2)小颖步行的速度 50米/分,
设小颖步行的速度为x米/分,则小颖父亲骑车的速度为4x米/分,
依题意,得10x+40x=2 500.
解得x=50.
(3)若小颖与爸爸相遇后坐爸爸的自行车赶回学校(假设爸爸骑自行车的速度不变)小颖能在上课前到达学校,理由如下:
两人相遇处离学校的距离为50×10=500米.
小颖和父亲相遇后,赶往学校的时间为
小颖来回花费的时间为10+2.5=12.5<15.
所以小颖能在上课前到达学校.
9.解:(1)函数 的图象如图.
函数的图象是双曲线,两个分支分别位于第一、二象限,在第二象限y随x的增大而增大,在第一象限y随x的增大而减小.
的图象向下平移两个单位长度得 的图象向右平移一个单位长度得( 图象略.
第 2 课时 函数的图象
基础知识夯实
知识沉淀
1.描点法画函数图象的一般步骤:
(1) ;
(2) ;
(3) .
2.函数的三种表示方法:
(1) 法;
(2)列表法;
(3)图象法.
基础过关
1.下列图象中,y不是x 的函数的是 ( )
2.小高从家门口骑车去单位上班,先走平路到达点A,再走上坡路到达点B,最后走下坡路到达工作单位,所用的时间与路程的关系如图所示.下班后,如果他沿原路返回,且走平路、上坡路、下坡路的速度分别保持和去上班时一致,那么他从单位到家门口需要的时间是 分钟.
典型案例探究
知识点1根据图象分析相关信息
【例题1】如图反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家.其中x表示时间,y 表示张强离家的距离.根据图象回答下列问题:(1)体育场离张强家 km,张强从家到体育馆用了 min;
(2)体育场离文具店 km,张强在文具店停留了 min;
(3)请计算:张强从文具店回家的平均速度是多少
【变式1】如图表示的是热带风暴从发生到结束的全过程.请结合图象回答下列问题:
(1)热带风暴从开始发生到结束共经历了 小时;
(2)从图象上看,风速在 (单位:小时)时间段内增大的最快,最大风速是 千米/时;
(3)风速从开始减小到最终停止,平均每小时减小多少千米
知识点 2 函数图象的画法
【例题2】某校办工厂,现在年产值是 15万元,计划今后每年增加2万元.
(1)写出年产值y(单位:万元)与年数x之间的函数关系式;
(2)画出函数图象;
(3)求5年后的年产值.
【变式2】在如图所示的平面直角坐标系中画出函数 的图象.
x
y
知识点 3 函数的三种表示方法
【例题3】已知等腰三角形的周长为12 cm,若底边长为y cm,一腰长为 x cm.
(1)确定y与x之间的函数关系式;
(2)确定x的取值范围;
(3)画出函数的图象.
【变式3】甲、乙两地相距160千米,某人开摩托车从甲地出发开往乙地,全程的平均速度是每小时 40千米,他与乙地的距离s(单位:千米)随开车的时间t(单位:小时)的变化而变化.
(1)用解析式法表示 s(单位:千米)与t(单位:小时)之间的函数关系,并指出自变量的取值范围;
(2)画出这个函数的图象.
课后作业
A 组
1.小刚从家去学校,先匀速步行到车站,等了几分钟后坐上了公交车,公交车匀速行驶一段时间后到达学校,小刚从家到学校行驶路程s(单位:m)与时间 t(单位:min)之间函数关系的大致图象是 ( )
2.在关系式 y=3x+5中,下列说法:①x是自变量,y是因变量;②x的数值可以任意选择;③y是变量,它的值与x无关;④y与x 的关系还可以用图象法表示,其中说法正确的是 ( )
A.①② B.①②④
C.①③ D.①④
3.赵先生手中有一张记录他从出生到 24 周岁期间的身高情况表(如下):
年龄x/岁 0 3 6 9 12 15 18 21 24
身高 h/cm 48 100 130 140 150 158 165 170 170.4
下列说法中错误的是 ( )
A.赵先生的身高增长速度总体上先快后慢
B.赵先生的身高在21岁以后基本不长了
C.赵 先生的身 高从 0 岁到 12 岁平 均每 年 增高12.5cm
D.赵先生的身高从 0 岁到 24 岁平均每年增高5.1 cm
4.已知方程 x—3y=12,用含 x 的代数式表示 y是 .
5.园林队在公园进行绿化,中间休息了一段时间.已知绿化面积S与时间t 的函数关系的图象如图所示,则休息后园林队绿化面积为 平方米.
6.某次大型活动,组委会启用无人机航拍活动过程,在操控无人机时应根据现场状况调节高度,已知无人机在上升和下降过程中速度相同,设无人机的飞行高度h(单位:米)与操控无人机的时间t(单位:分钟)之间的关系如图中的实线所示,根据图象回答下列问题:
(1)图中的自变量是 ,因变量是 ;
(2)无人机在75米高的上空停留的时间是 分钟;
(3)在上升或下降过程中,无人机的速度为 米/分;
(4)图中a表示的数是 ;b表示的数是 ;
(5)图中点 A 表示 ·
B 组
7.父亲告诉小明:“距离地面越远,温度越低,”并给小明出示了下面的表格.
距离地面高度/千米 0 1 2 3 4 5
温度/℃ 20 14 8 2 -4 -10
根据上表,父亲还给小明出了下面几个问题,你和小明一起回答.
(1)上表反映了哪两个变量之间的关系 哪个是自变量 哪个是因变量
(2)如果用h表示距离地面的高度,用t 表示温度,那么随着h的变化,t是怎么变化的
(3)你知道距离地面5千米的高空温度是多少吗
(4)你能猜出距离地面6 千米的高空温度是多少吗
8.某天,小颖到校后发现有学习用品遗忘在家中,此时离上课还有15分钟,于是立即步行回家去取.同时小颖的爸爸从家中出发骑自行车给她送学习用品,两人在途中相遇,在这个过程中,小颖和爸爸两人离学校的距离s(单位:m)与所用时间t(单位:min)之间的关系如图所示,若爸爸骑自行车的速度是小颖步行的4倍,根据图中提供的信息,回答下列问题:
(1)学校离家的距离是 米,爸爸出发 分钟后与小颖相遇;
(2)请求出小颖步行的速度;
(3)若小颖与爸爸相遇后坐爸爸的自行车赶回学校(假设爸爸骑自行车的速度不变)小颖能在上课前到达学校吗 请说明理由.
C 组
9.函数可揭示事物变化规律,它有多种表示形式.如表格、图象、表达式等,这些表示形式各有优势.图象法直观、列表法具体、表达式精确.若把三者结合起来,则能更全面深刻地理解变量之间的关系.试解决下列问题.
(1)已知函数表达式 你能说出它的图象具有的一些特征吗 试画出它的图象;
(2)试说明下列函数的图象与 的图象之间的位置关系,并在同一平面直角坐标系中画出它们的图象.
第 2课时 函数的图象
【基础知识夯实】
知识沉淀
1.(1)列表 (2)描点 (3)连线
2.(1)解析式
基础过关
1. A 2.15
【典型案例探究】
例题1 (1)2.5 15 (2)1 20 (3) / km/min
变式1 解:(1)16.
由图象可得,热带风暴从开始发生到结束共经历了16 个小时.
(2)2~5 54
从图象上看,风速在2~5(小时)时间段内增大的最快,最大风速是 54 千米/时.
(3)风速从开始减小到最终停止,平均每小时减小:54÷(16-10)=54÷6=9(千米/时),即风速从开始减小到最终停止,平均每小时减小9千米/时.
例题2解:(1)函数关系式为y=15+2x(x≥0).
(2)列表:
x 0 1 2 3 4 5 6 ··
y=15+2x| 15 17 19 21 23 25 27
描点,连线,得出函数图象,如图.
变式2 略
例题3 解:(1)依题意,得 y=12-2x.
解得3
x 3 4 5 5.5 6
y 6 4 2 1 0
描点,连线.其图象如图.
变式3 解:(1)s=160-40t,0≤1≤4.
(2)图象略.
【课后作业】
1. B 2. B 3. C 4. y= x--4 5.100
6.解:(1)自变量是时间(或t),因变量是高度(或h).
(2)5 (3)25 (4)2 15
(5)图中点 A 表示在第6 分钟时,无人机的飞行高度为50 米.
7.解:(1)上表反映了温度和距地面高度之间的关系,高度是自变量,温度是因变量.
(2)由表可知,每上升1千米,温度降低6摄氏度,可得解析式为t=20-6h.
(3)由表可知,距地面5千米时,温度为零下 10摄氏度.
(4)将t=6代入h=20-6t,可得t=20-6×6=-16.
8.解:(1)2 500 10
(2)小颖步行的速度 50米/分,
设小颖步行的速度为x米/分,则小颖父亲骑车的速度为4x米/分,
依题意,得10x+40x=2 500.
解得x=50.
(3)若小颖与爸爸相遇后坐爸爸的自行车赶回学校(假设爸爸骑自行车的速度不变)小颖能在上课前到达学校,理由如下:
两人相遇处离学校的距离为50×10=500米.
小颖和父亲相遇后,赶往学校的时间为
小颖来回花费的时间为10+2.5=12.5<15.
所以小颖能在上课前到达学校.
9.解:(1)函数 的图象如图.
函数的图象是双曲线,两个分支分别位于第一、二象限,在第二象限y随x的增大而增大,在第一象限y随x的增大而减小.
的图象向下平移两个单位长度得 的图象向右平移一个单位长度得( 图象略.
