初中数学人教版八年级下册 第十八章 平行四边形 章末整合 感知中考(含答案)
文档属性
| 名称 | 初中数学人教版八年级下册 第十八章 平行四边形 章末整合 感知中考(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-03 20:48:39 | ||
图片预览



文档简介
章末整合·感知中考
知识网络
二内容归纳
1.三角形的中位线定义:三角形两边中点的连线叫做三角形的中位线.
2.三角形的中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.
3.四边形的性质与判定:
名称 图形 定义 性质 判定
平行四边形 两 组 对 边 分别平 行的 四边 形 叫 做 平行四边形 (1)对边平行、对边相等; (2)对角相等; (3)对角线互相平分 (1)两组对边分别平行的四边形是平行四边形; (2)两组对边分别相等的四边形是平行四边形; (3)一组对边平行且相等的四边形是平行四边形; (4)两组对角分别相等的四边形是平行四边形; (5)对角线互相平分的四边形是平行四边形
矩形 有 一 个 角 是直角 的 平 行四边 形 叫做矩形 (1)对边平行、对边相等; (2)四个角都是直角; (3)对角线互相平分且相等 (1)有一个角是直角的平行四边形是矩形; (2)对角线相等的平行四边形是矩形; (3)三个角都是直角的四边形是矩形
菱形 一 组 邻 边 相等 的 平 行 四边 形 叫 做菱形 (1)对边平行; (2)四条边相等; (3)对角线互相垂直平分,并且每条对角线平分一组对角 (1)一组邻边相等的平行四边形是菱形; (2)对角线互相垂直的平行四边形是菱形; (3)四条边相等的四边形是菱形
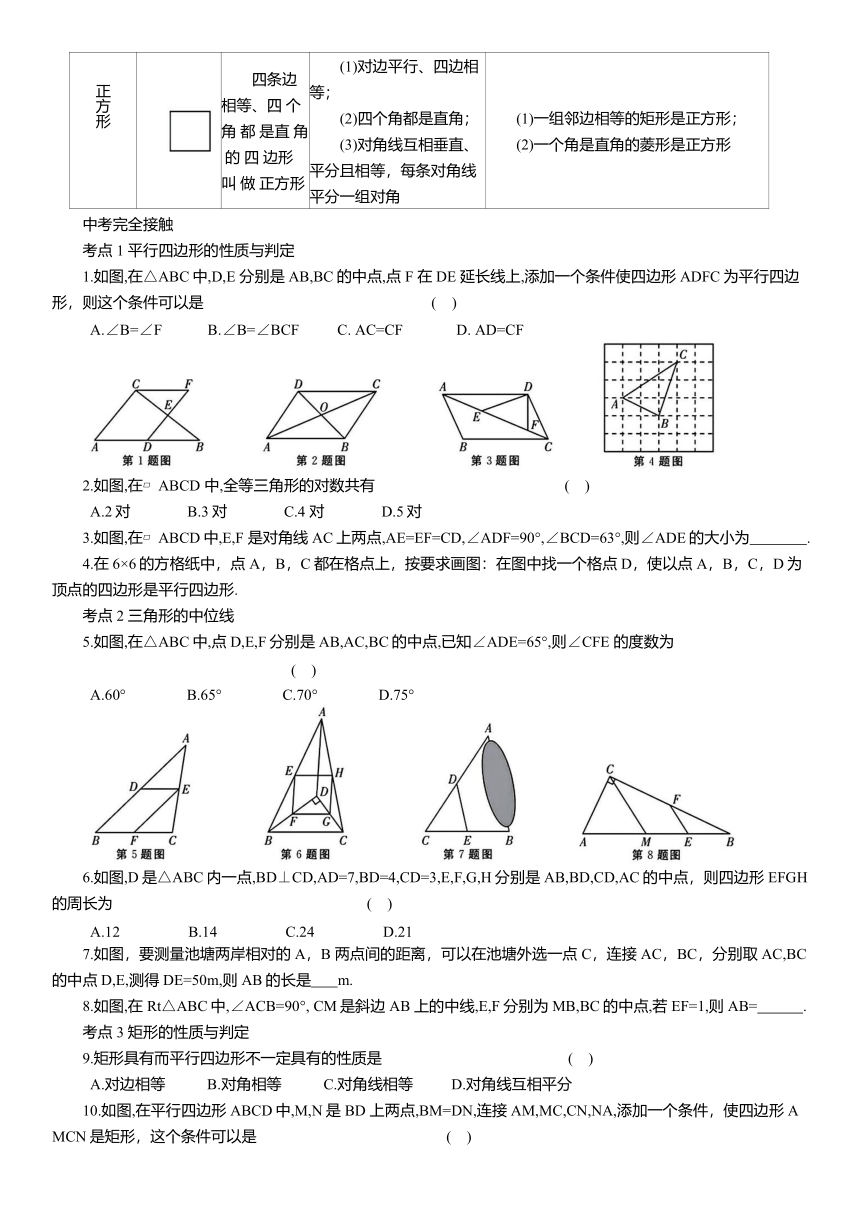
正方形 四条边相等、四 个 角 都 是直 角 的 四 边形 叫 做 正方形 (1)对边平行、四边相等; (2)四个角都是直角; (3)对角线互相垂直、平分且相等,每条对角线平分一组对角 (1)一组邻边相等的矩形是正方形; (2)一个角是直角的菱形是正方形
中考完全接触
考点 1 平行四边形的性质与判定
1.如图,在△ABC中,D,E 分别是AB,BC的中点,点 F 在DE 延长线上,添加一个条件使四边形ADFC为平行四边形,则这个条件可以是 ( )
A.∠B=∠F B.∠B=∠BCF C. AC=CF D. AD=CF
2.如图,在 ABCD 中,全等三角形的对数共有 ( )
A.2对 B.3对 C.4 对 D.5对
3.如图,在 ABCD中,E,F 是对角线AC上两点,AE=EF=CD,∠ADF=90°,∠BCD=63°,则∠ADE的大小为 .
4.在6×6的方格纸中,点A,B,C都在格点上,按要求画图:在图中找一个格点D,使以点A,B,C,D为顶点的四边形是平行四边形.
考点2 三角形的中位线
5.如图,在△ABC中,点D,E,F分别是AB,AC,BC的中点,已知∠ADE=65°,则∠CFE 的度数为 ( )
A.60° B.65° C.70° D.75°
6.如图,D是△ABC内一点,BD⊥CD,AD=7,BD=4,CD=3,E,F,G,H分别是AB,BD,CD,AC的中点,则四边形 EFGH的周长为 ( )
A.12 B.14 C.24 D.21
7.如图,要测量池塘两岸相对的A,B 两点间的距离,可以在池塘外选一点 C,连接AC,BC,分别取AC,BC的中点D,E,测得DE=50m,则AB的长是 m.
8.如图,在 Rt△ABC中,∠ACB=90°, CM是斜边AB 上的中线,E,F分别为MB,BC的中点,若EF=1,则 AB= .
考点3 矩形的性质与判定
9.矩形具有而平行四边形不一定具有的性质是 ( )
A.对边相等 B.对角相等 C.对角线相等 D.对角线互相平分
10.如图,在平行四边形 ABCD中,M,N是 BD 上两点,BM=DN,连接AM,MC,CN,NA,添加一个条件,使四边形AMCN是矩形,这个条件可以是 ( )
B. MB=MO
C. BD⊥AC
D.∠AMB=∠CND
11如图,在矩形ABCD 中对角线AC 与BD 相交于点O,CE⊥BD,垂足为点 E,CE=5,且 EO=2DE,则AD的长为 ( )
A.5 B.6 C.10
12.如图,在矩形 ABCD中,AB=10,AD=6,E为BC上一点,把△CDE沿DE 折叠,使点 C 落在AB 边上的F 处,则CE的长为 .
考点 4 菱形的性质与判定
13.如图,四边形ABCD的两条对角线相交于点O,且互相平分.添加下列条件,仍不能判定四边形ABCD为菱形的是 ( )
A. AC⊥BD B. AB=AD C. AC=BD D.∠ABD=∠CBD
14.如图,菱形ABCD 的对角线AC,BD交于点O,AC=4,BD=16,将△ABO沿点A 到点C 的方向平移,得到△A'B'O',当点 A'与点 C 重合时,点 A 与点 B'之间的距离为 ( )
A.6 B.8 C. 10 D.12
15.已知菱形ABCD,E,F是动点,边长为4,BE=AF,∠BAD=120°,则下列结论正确的有 ( )①△BEC≌△AFC ;②△ECF为等边三角形;③∠AGE=∠AFC;④若AF=1,则
A.1 个 B.2个 C.3 个 D.4 个
16.如图,已知菱形ABCD的对角线AC,BD交于点O,E为BC的中点,若OE=3,则菱形的周长为
考点5 正方形的性质与判定
17.如图,在正方形ABCD中,点 E,F 分别在BC,CD上,BE=CF,则图中与∠AEB 相等的角的个数是 ( )
A.1 B.2 C.3 D.4
18.如图,AC,BD 是四边形ABCD 的对角线,点E,F 分别是AD,BC 的中点,点 M,N分别是AC,BD的中点,连接EM,MF,FN,NE,要使四边形 EMFN为正方形,则需添加的条件是 ( )
A. AB=CD,AB⊥CD B. AB=CD,AD=BC C. AB=CD,AC⊥BD D. AB=CD,AD∥BC
19.如图,正方形ABCD 的边长为4,延长CB 至E 使 EB=2,以EB 为边在上方作正方形EFGB,延长 FG 交 DC 于M,连接 AM,AF,H 为 AD 的中点,连接FH 分别与AB,AM交于点 N,K.则下列结论:①△ANH≌△GNF;②∠AFN=∠HFG;③FN=2NK;④S△AFN :S△ADM=1:4.其中正确的结论有
A.1个 B.2 个 C.3 个 D.4 个
如图,在正方形ABCD中,BE=1,将BC 沿CE 翻折,使点 B 对应点刚好落在对角线AC 上,将AD 沿AF 翻折,使点 D对应点落在对角线AC 上,则EF= .
考点6 平行四边形、矩形、菱形、正方形的综合应用
21如图,在正方形ABCD中,点 E,F 分别在边CD,AD上,且
(1)求证:
(2)若 ,求四边形 BEDF 的面积.
22.已知:如图,在平行四边形中, E,F 分别为垂足.
(1)求证:
(2)求证:四边形AECF是矩形.
23.如图,正方形ABCD,点E,F 分别在AD,CD上,且 AF与BE 相交于点G.
(1)求证:
(2)若 ,求 AG 的长.
24.如图,矩形EFGH 的顶点E,G 分别在菱形ABCD 的边AD,BC上,顶点 F,H 在菱形ABCD 的对角线 BD 上.
(1)求证:
(2)若 E 为 AD 中点, ,求菱形 ABCD的周长.
25如图,E,F 分别是正方形ABCD 的边CB,DC 延长线上的点,且 ,过点 E 作 交正方形外角的平分线CG 于点G,连接GF.求证:
(2)四边形 BEGF是平行四边形.
26.如图(1),对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解:如图(2),在四边形 ABCD中, ,四边形 ABCD 是垂美四边形吗 请说明理由;
(2)性质探究:如图(1),四边形ABCD的对角线AC,BD交于点O, 试证明:
(3)解决问题:如图(3),分别以 的直角边AC 和斜边AB 为边向外作正方形ACFG 和正方形ABDE,连接CE,BG,GE.已知. ,求 GE 的长.
章末整合·感知中考
【中考完全接触】
1. B 2. C 3.21° 4.略 5. B 6. A 7.100 8.49. C 10. A 11. A 12. 13. C 14. C 15. D16.24 17. C 18. A 19. C 20.
21.(1)证明:在△ABF和△CBE中,
所以△ABF≌△CBE(SAS).
(2)解:由已知可得正方形ABCD面积为16,
所以四边形 BEDF的面积为16-2×2=12.
22.证明:(1)∵四边形ABCD是平行四边形,
∴∠B=∠D,AB=CD.
∵AE⊥BC,CF⊥AD,
∴∠AEB=∠CFD=90°.
在△ABE和△CDF 中,
∴△ABE≌△CDF(AAS).
(2)∵AE⊥BC,CF⊥AD,
∴∠AEC=∠AFC=90°.
∵四边形ABCD是平行四边形,
∴AD∥BC.∴∠EAF=180°-∠AEC=90°.
∴∠EAF=∠AEC=∠AFC=90°.
∴四边形AECF是矩形.
23.(1)证明:∵四边形ABCD是正方形,
∴∠BAE=∠ADF=90°,AB=AD=CD.
∵DE=CF,∴AE=DF.
在△BAE 和△ADF中,
∴△BAE≌△ADF(SAS).
∴BE=AF.
(2)解:由(1)得△BAE≌△ADF,
∴∠EBA=∠FAD.
∴∠GAE+∠AEG=90°.
∴∠AGE=90°.
∵AB=4,DE=1,∴AE=3.
在 Rt△ABE中,
24.(1)证明:∵四边形 EFGH 是矩形,
∴EH=FG,EH∥FG.
∴∠GFH=∠EHF.
∵∠BFG=180°-∠GFH,∠DHE=180°-∠EHF,
∴∠BFG=∠DHE.
∵四边形ABCD是菱形,
∴AD∥BC.∴∠GBF=∠EDH.
∴△BGF≌△DEH(AAS).
∴BG=DE.
(2)解:连接EG.
∵四边形ABCD是菱形,
∴AD=BC,AD∥BC.
∵E为AD中点,
∴AE=ED.
∵BG=DE,∴AE=BG.又 AE∥BG,
∴四边形 ABGE 是平行四边形,
∴AB=EG.
∵EG=FH=2,∴AB=2.
∴菱形ABCD的周长=8.
25.证明:(1)∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠BCD=90°.
∴∠ABE=∠BCF=90°.
在△ABE和△BCF 中.
∴△ABE≌△BCF(SAS).
∴AE=BF,∠BAE=∠CBF.
∵EG∥BF,∴∠CBF=∠CEG.
∵∠BAE+∠BEA=90°,
∴∠CEG+∠BEA=90°.∴AE⊥EG.
又 EG∥BF,∴AE⊥BF.
(2)如图,延长 AB 至点 P,使BP=BE,连接 EP.
则AP=CE,∠EBP=90°,∴∠P=45°.
∵CG为正方形ABCD 外角的平分线,
∴∠ECG=45°.
∴∠P=∠ECG.
由(1)得∠BAE=∠CEG,
在△APE和△ECG中,
∴△APE≌△ECG(ASA).
∴AE=EG.
∵AE=BF,∴EG=BF.
∵EG∥BF,
∴四边形 BEGF 是平行四边形.
26.解:(1)四边形ABCD 是垂美四边形.理由如下:连接 AC,BD,如图(1).
∵AB=AD,
∴点 A 在线段BD 的垂直平分线上.
∵CB=CD,
∴点C在线段BD 的垂直平分线上.
∴直线 AC 是线段 BD 的垂直平分线.
∴AC⊥BD,即四边形ABCD是垂美四边形.
(2)∵AC⊥BD,
∴∠AOD=∠AOB=∠BOC=∠COD=90°.
由勾股定理,得AB +CD =OA +OB +OC +OD ,
(3)连接CG,BE,如图(2).
∵∠CAG=∠BAE=90°,∴ ∠CAG + ∠BAC =∠BAE+∠BAC,即∠GAB=∠CAE.
在△GAB和△CAE中,
∴△GAB≌△CAE(SAS).
∴∠ABG=∠AEC.
又∠AEC+∠AME=90°,∠AME=∠BMN,
∴∠ABG+∠BMN=90°,即CE⊥BG.
∴四边形 CGEB 是垂美四边形.
由(2)得(
∵AC=4,AB=5,
知识网络
二内容归纳
1.三角形的中位线定义:三角形两边中点的连线叫做三角形的中位线.
2.三角形的中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.
3.四边形的性质与判定:
名称 图形 定义 性质 判定
平行四边形 两 组 对 边 分别平 行的 四边 形 叫 做 平行四边形 (1)对边平行、对边相等; (2)对角相等; (3)对角线互相平分 (1)两组对边分别平行的四边形是平行四边形; (2)两组对边分别相等的四边形是平行四边形; (3)一组对边平行且相等的四边形是平行四边形; (4)两组对角分别相等的四边形是平行四边形; (5)对角线互相平分的四边形是平行四边形
矩形 有 一 个 角 是直角 的 平 行四边 形 叫做矩形 (1)对边平行、对边相等; (2)四个角都是直角; (3)对角线互相平分且相等 (1)有一个角是直角的平行四边形是矩形; (2)对角线相等的平行四边形是矩形; (3)三个角都是直角的四边形是矩形
菱形 一 组 邻 边 相等 的 平 行 四边 形 叫 做菱形 (1)对边平行; (2)四条边相等; (3)对角线互相垂直平分,并且每条对角线平分一组对角 (1)一组邻边相等的平行四边形是菱形; (2)对角线互相垂直的平行四边形是菱形; (3)四条边相等的四边形是菱形
正方形 四条边相等、四 个 角 都 是直 角 的 四 边形 叫 做 正方形 (1)对边平行、四边相等; (2)四个角都是直角; (3)对角线互相垂直、平分且相等,每条对角线平分一组对角 (1)一组邻边相等的矩形是正方形; (2)一个角是直角的菱形是正方形
中考完全接触
考点 1 平行四边形的性质与判定
1.如图,在△ABC中,D,E 分别是AB,BC的中点,点 F 在DE 延长线上,添加一个条件使四边形ADFC为平行四边形,则这个条件可以是 ( )
A.∠B=∠F B.∠B=∠BCF C. AC=CF D. AD=CF
2.如图,在 ABCD 中,全等三角形的对数共有 ( )
A.2对 B.3对 C.4 对 D.5对
3.如图,在 ABCD中,E,F 是对角线AC上两点,AE=EF=CD,∠ADF=90°,∠BCD=63°,则∠ADE的大小为 .
4.在6×6的方格纸中,点A,B,C都在格点上,按要求画图:在图中找一个格点D,使以点A,B,C,D为顶点的四边形是平行四边形.
考点2 三角形的中位线
5.如图,在△ABC中,点D,E,F分别是AB,AC,BC的中点,已知∠ADE=65°,则∠CFE 的度数为 ( )
A.60° B.65° C.70° D.75°
6.如图,D是△ABC内一点,BD⊥CD,AD=7,BD=4,CD=3,E,F,G,H分别是AB,BD,CD,AC的中点,则四边形 EFGH的周长为 ( )
A.12 B.14 C.24 D.21
7.如图,要测量池塘两岸相对的A,B 两点间的距离,可以在池塘外选一点 C,连接AC,BC,分别取AC,BC的中点D,E,测得DE=50m,则AB的长是 m.
8.如图,在 Rt△ABC中,∠ACB=90°, CM是斜边AB 上的中线,E,F分别为MB,BC的中点,若EF=1,则 AB= .
考点3 矩形的性质与判定
9.矩形具有而平行四边形不一定具有的性质是 ( )
A.对边相等 B.对角相等 C.对角线相等 D.对角线互相平分
10.如图,在平行四边形 ABCD中,M,N是 BD 上两点,BM=DN,连接AM,MC,CN,NA,添加一个条件,使四边形AMCN是矩形,这个条件可以是 ( )
B. MB=MO
C. BD⊥AC
D.∠AMB=∠CND
11如图,在矩形ABCD 中对角线AC 与BD 相交于点O,CE⊥BD,垂足为点 E,CE=5,且 EO=2DE,则AD的长为 ( )
A.5 B.6 C.10
12.如图,在矩形 ABCD中,AB=10,AD=6,E为BC上一点,把△CDE沿DE 折叠,使点 C 落在AB 边上的F 处,则CE的长为 .
考点 4 菱形的性质与判定
13.如图,四边形ABCD的两条对角线相交于点O,且互相平分.添加下列条件,仍不能判定四边形ABCD为菱形的是 ( )
A. AC⊥BD B. AB=AD C. AC=BD D.∠ABD=∠CBD
14.如图,菱形ABCD 的对角线AC,BD交于点O,AC=4,BD=16,将△ABO沿点A 到点C 的方向平移,得到△A'B'O',当点 A'与点 C 重合时,点 A 与点 B'之间的距离为 ( )
A.6 B.8 C. 10 D.12
15.已知菱形ABCD,E,F是动点,边长为4,BE=AF,∠BAD=120°,则下列结论正确的有 ( )①△BEC≌△AFC ;②△ECF为等边三角形;③∠AGE=∠AFC;④若AF=1,则
A.1 个 B.2个 C.3 个 D.4 个
16.如图,已知菱形ABCD的对角线AC,BD交于点O,E为BC的中点,若OE=3,则菱形的周长为
考点5 正方形的性质与判定
17.如图,在正方形ABCD中,点 E,F 分别在BC,CD上,BE=CF,则图中与∠AEB 相等的角的个数是 ( )
A.1 B.2 C.3 D.4
18.如图,AC,BD 是四边形ABCD 的对角线,点E,F 分别是AD,BC 的中点,点 M,N分别是AC,BD的中点,连接EM,MF,FN,NE,要使四边形 EMFN为正方形,则需添加的条件是 ( )
A. AB=CD,AB⊥CD B. AB=CD,AD=BC C. AB=CD,AC⊥BD D. AB=CD,AD∥BC
19.如图,正方形ABCD 的边长为4,延长CB 至E 使 EB=2,以EB 为边在上方作正方形EFGB,延长 FG 交 DC 于M,连接 AM,AF,H 为 AD 的中点,连接FH 分别与AB,AM交于点 N,K.则下列结论:①△ANH≌△GNF;②∠AFN=∠HFG;③FN=2NK;④S△AFN :S△ADM=1:4.其中正确的结论有
A.1个 B.2 个 C.3 个 D.4 个
如图,在正方形ABCD中,BE=1,将BC 沿CE 翻折,使点 B 对应点刚好落在对角线AC 上,将AD 沿AF 翻折,使点 D对应点落在对角线AC 上,则EF= .
考点6 平行四边形、矩形、菱形、正方形的综合应用
21如图,在正方形ABCD中,点 E,F 分别在边CD,AD上,且
(1)求证:
(2)若 ,求四边形 BEDF 的面积.
22.已知:如图,在平行四边形中, E,F 分别为垂足.
(1)求证:
(2)求证:四边形AECF是矩形.
23.如图,正方形ABCD,点E,F 分别在AD,CD上,且 AF与BE 相交于点G.
(1)求证:
(2)若 ,求 AG 的长.
24.如图,矩形EFGH 的顶点E,G 分别在菱形ABCD 的边AD,BC上,顶点 F,H 在菱形ABCD 的对角线 BD 上.
(1)求证:
(2)若 E 为 AD 中点, ,求菱形 ABCD的周长.
25如图,E,F 分别是正方形ABCD 的边CB,DC 延长线上的点,且 ,过点 E 作 交正方形外角的平分线CG 于点G,连接GF.求证:
(2)四边形 BEGF是平行四边形.
26.如图(1),对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解:如图(2),在四边形 ABCD中, ,四边形 ABCD 是垂美四边形吗 请说明理由;
(2)性质探究:如图(1),四边形ABCD的对角线AC,BD交于点O, 试证明:
(3)解决问题:如图(3),分别以 的直角边AC 和斜边AB 为边向外作正方形ACFG 和正方形ABDE,连接CE,BG,GE.已知. ,求 GE 的长.
章末整合·感知中考
【中考完全接触】
1. B 2. C 3.21° 4.略 5. B 6. A 7.100 8.49. C 10. A 11. A 12. 13. C 14. C 15. D16.24 17. C 18. A 19. C 20.
21.(1)证明:在△ABF和△CBE中,
所以△ABF≌△CBE(SAS).
(2)解:由已知可得正方形ABCD面积为16,
所以四边形 BEDF的面积为16-2×2=12.
22.证明:(1)∵四边形ABCD是平行四边形,
∴∠B=∠D,AB=CD.
∵AE⊥BC,CF⊥AD,
∴∠AEB=∠CFD=90°.
在△ABE和△CDF 中,
∴△ABE≌△CDF(AAS).
(2)∵AE⊥BC,CF⊥AD,
∴∠AEC=∠AFC=90°.
∵四边形ABCD是平行四边形,
∴AD∥BC.∴∠EAF=180°-∠AEC=90°.
∴∠EAF=∠AEC=∠AFC=90°.
∴四边形AECF是矩形.
23.(1)证明:∵四边形ABCD是正方形,
∴∠BAE=∠ADF=90°,AB=AD=CD.
∵DE=CF,∴AE=DF.
在△BAE 和△ADF中,
∴△BAE≌△ADF(SAS).
∴BE=AF.
(2)解:由(1)得△BAE≌△ADF,
∴∠EBA=∠FAD.
∴∠GAE+∠AEG=90°.
∴∠AGE=90°.
∵AB=4,DE=1,∴AE=3.
在 Rt△ABE中,
24.(1)证明:∵四边形 EFGH 是矩形,
∴EH=FG,EH∥FG.
∴∠GFH=∠EHF.
∵∠BFG=180°-∠GFH,∠DHE=180°-∠EHF,
∴∠BFG=∠DHE.
∵四边形ABCD是菱形,
∴AD∥BC.∴∠GBF=∠EDH.
∴△BGF≌△DEH(AAS).
∴BG=DE.
(2)解:连接EG.
∵四边形ABCD是菱形,
∴AD=BC,AD∥BC.
∵E为AD中点,
∴AE=ED.
∵BG=DE,∴AE=BG.又 AE∥BG,
∴四边形 ABGE 是平行四边形,
∴AB=EG.
∵EG=FH=2,∴AB=2.
∴菱形ABCD的周长=8.
25.证明:(1)∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠BCD=90°.
∴∠ABE=∠BCF=90°.
在△ABE和△BCF 中.
∴△ABE≌△BCF(SAS).
∴AE=BF,∠BAE=∠CBF.
∵EG∥BF,∴∠CBF=∠CEG.
∵∠BAE+∠BEA=90°,
∴∠CEG+∠BEA=90°.∴AE⊥EG.
又 EG∥BF,∴AE⊥BF.
(2)如图,延长 AB 至点 P,使BP=BE,连接 EP.
则AP=CE,∠EBP=90°,∴∠P=45°.
∵CG为正方形ABCD 外角的平分线,
∴∠ECG=45°.
∴∠P=∠ECG.
由(1)得∠BAE=∠CEG,
在△APE和△ECG中,
∴△APE≌△ECG(ASA).
∴AE=EG.
∵AE=BF,∴EG=BF.
∵EG∥BF,
∴四边形 BEGF 是平行四边形.
26.解:(1)四边形ABCD 是垂美四边形.理由如下:连接 AC,BD,如图(1).
∵AB=AD,
∴点 A 在线段BD 的垂直平分线上.
∵CB=CD,
∴点C在线段BD 的垂直平分线上.
∴直线 AC 是线段 BD 的垂直平分线.
∴AC⊥BD,即四边形ABCD是垂美四边形.
(2)∵AC⊥BD,
∴∠AOD=∠AOB=∠BOC=∠COD=90°.
由勾股定理,得AB +CD =OA +OB +OC +OD ,
(3)连接CG,BE,如图(2).
∵∠CAG=∠BAE=90°,∴ ∠CAG + ∠BAC =∠BAE+∠BAC,即∠GAB=∠CAE.
在△GAB和△CAE中,
∴△GAB≌△CAE(SAS).
∴∠ABG=∠AEC.
又∠AEC+∠AME=90°,∠AME=∠BMN,
∴∠ABG+∠BMN=90°,即CE⊥BG.
∴四边形 CGEB 是垂美四边形.
由(2)得(
∵AC=4,AB=5,
