初中数学人教版八年级下册18.2 特殊的平行四边形(第 3课时) 三角形的中位线同步(分层)练习(含答案)
文档属性
| 名称 | 初中数学人教版八年级下册18.2 特殊的平行四边形(第 3课时) 三角形的中位线同步(分层)练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 386.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-03 21:59:43 | ||
图片预览


文档简介
第 3课时 三角形的中位线
基础知识夯实
知识沉淀
1.三角形的中位线定义:连接三角形 叫做三角形的中位线.
2.三角形的中位线定理:三角形的中位线 于第三边,并且等于 .
基础过关
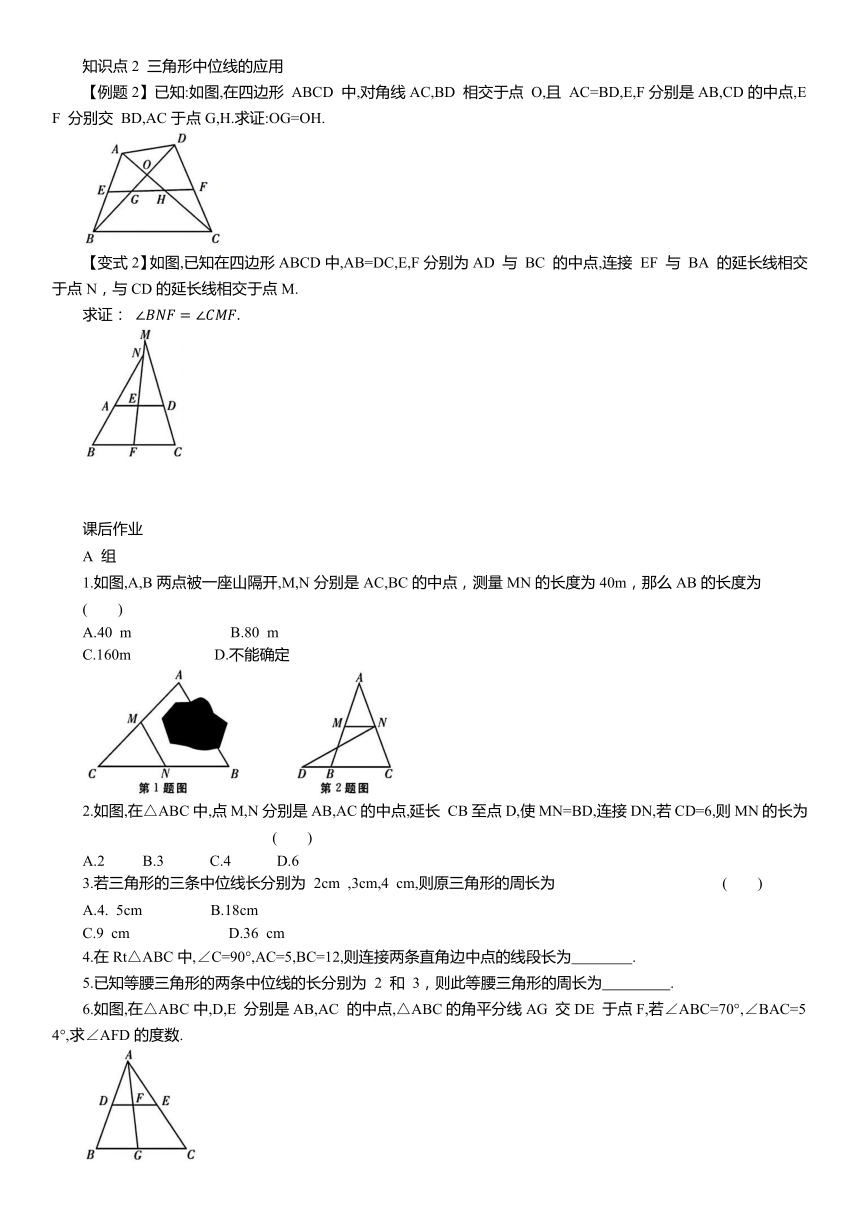
1.如图,在△ABC中,D,E分别是边AB,AC的中点,若 BC=6,则 DE 的长为 ( )
A.2 B.3 C.4 D.6
2.如图,在△MBN中,已知:BM=6,BN=7,MN=10,点A,C,D分别是MB,NB,MN的中点,则四边形ABCD的周长是 .
典型案例探究
知识点 1 三角形中位线的性质
【例题1】如图,M是△ABC 的边BC 的中点,AN 平分∠BAC,BN⊥AN 于点N,延长BN 交AC 于点D,已知 AB=10,AC=16.
(1)求证:BN=DN;
(2)求 MN 的长.
【变式1】如图,等边三角形ABC的边长是2,D,E分别为AB,AC的中点,过点 E 作EF∥CD交BC 的延长线于点 F,连接CD.
(1)求证:DE=CF;
(2)求 EF 的长.
知识点2 三角形中位线的应用
【例题2】已知:如图,在四边形 ABCD 中,对角线AC,BD 相交于点 O,且 AC=BD,E,F分别是AB,CD的中点,EF 分别交 BD,AC于点G,H.求证:OG=OH.
【变式2】如图,已知在四边形ABCD中,AB=DC,E,F分别为AD 与 BC 的中点,连接 EF 与 BA 的延长线相交于点N,与CD的延长线相交于点M.
求证:
课后作业
A 组
1.如图,A,B两点被一座山隔开,M,N分别是AC,BC的中点,测量MN的长度为40m,那么AB的长度为
( )
A.40 m B.80 m
C.160m D.不能确定
2.如图,在△ABC中,点M,N分别是AB,AC的中点,延长 CB至点D,使MN=BD,连接DN,若CD=6,则MN的长为 ( )
A.2 B.3 C.4 D.6
3.若三角形的三条中位线长分别为 2cm ,3cm,4 cm,则原三角形的周长为 ( )
A.4. 5cm B.18cm
C.9 cm D.36 cm
4.在Rt△ABC中,∠C=90°,AC=5,BC=12,则连接两条直角边中点的线段长为 .
5.已知等腰三角形的两条中位线的长分别为 2 和 3,则此等腰三角形的周长为 .
6.如图,在△ABC中,D,E 分别是AB,AC 的中点,△ABC的角平分线AG 交DE 于点F,若∠ABC=70°,∠BAC=54°,求∠AFD的度数.
7.如图, 中,点 D 是AB 的中点,DE∥BC,求证:点 E 是 AC 的中点.
B 组
8.已知在△ABC 中,D 为AB 的中点,E 为AC 上一点,AE=2CE,CD,BE交于O点,OE=2 厘米.求BO 的长.
9.如图,在 中,D 为AC 上一点, F 是AD 的中点,M 为 BC 的中点,连接 MF 并延长交BA 延长线于点E,G 为EF 的中点,求证:AG⊥ME.
C
C 组
10.如图(1),BD,CE 分别是△ABC 的外角平分线,过点 A 作AF⊥BD,AG⊥CE,垂足分别为 F,G,连接FG,延长AF,AG,与直线 BC 相交于M,N.
(1)求证:
(2)如图(2),BD,CE 分别是△ABC 的内角平分线,过点 A 作 AF⊥BD,AG⊥CE,垂足分别为 F,G,连接 FG,则线段 FG 与△ABC 的三边又有怎样的数量关系 请写出你的猜想并说明理由.
第 3 课时 三角形的中位线
【基础知识夯实】
知识沉淀
1.两边中点的线段
2.平行 第三边的一半
基础过关
1. B 2.13
【典型案例探究】
例题1 (1)证明:∵AN平分∠BAC,∴∠1=∠2.
∵BN⊥AN,∴∠ANB=∠AND.
在△ABN和△ADN中,
∴△ABN≌△ADN(ASA).
∴BN=DN.
(2)解:∵△ABN≌△ADN,
∴AD=AB=10,DN=NB.
∴CD=AC-AD=16-10=6.
又∵点 M是BC中点,
∴MN是△BDC的中位线.
变式1 (1)证明:∵D,E 分别为AB,AC的中点,
∵EF∥CD,∴四边形DEFC是平行四边形.
∴DE=CF.
(2)解:∵四边形 DEFC是平行四边形,∴DC=EF.
∵D 为AB 的中点,等边三角形 ABC的边长是 2,
∴BD=AD=1,CD⊥AB,BC=2.
例题2证明:取 BC边的中点M,连接EM,FM,∵M,F分别是BC,CD的中点,
∴MF∥BD,MF=
同理,ME∥AC,ME
∵AC=BD,
∴ME=MF.
∴∠MEF=∠MFE.
∵MF∥BD,∴∠MFE=∠OGH.同理,∠MEF=∠OHG.
∴∠OGH=∠OHG.
∴OG=OH.
变式2证明:如图,连接AC,取AC的中点K,连接 EK,FK,
∵AE=ED,AK=KC,
同理, FK ∥ AB, FK =
=EK.
∴∠FEK=∠EFK.
∵EK∥DC,∴∠CMF=∠FEK.
∵FK∥AB,∴∠BNF=∠EFK.
∴∠BNF=∠CMF.
【课后作业】
1. B 2. A 3. B 4.6.5 5.14或16
6.解:∵∠BAC=54°,AG平分∠BAC,
∴∠BGA=180°-∠ABC-∠BAG=83°.
又∵点D,E分别是AB,AC的中点,∴DE∥BC.
∴∠AFD=∠BGA=83°.
7. 证明: 如图,取 BC 的中点 F,连接 DF.
∵点D 是AB 的中点,
又 DE∥BC,∴四边形 CEDF 是平行四边形.
∴DF=CE.
即点 E 是AC 的中点.
8.解:取 BE的中点 F,连接 DF,如图.
∵D为AB 的中点,
∴ ∠DFO = ∠OEC, ∠OCE=∠ODF.
又∵AE=2EC,∴DF=EC.
∴△DFO≌△CEO.
∴EO=FO.
∵BF=FE,∴BO=3EO=3×2=6厘米.
9.证明:连接BD,取BD的中点为O,连接FO,MO,∵F 是AD 的中点,M为BC的中点,
∴MO是△BCD 的中位线, FO 是△ABD 的中位线.
AB, MO∥AC, OF∥AB.
∵AB=CD,∴MO=FO.∴∠OFM=∠OMF.
∵OF∥AB,∴∠OFM=∠AEF.
∵OM∥AC,∴∠OMF=∠CFM=∠AFE.
∴∠AEF=∠AFE.∴AE=AF.
∵G为EF 的中点,∴AG⊥ME.
10.(1)证明:∵BD⊥AF,∴∠AFB=∠MFB=90°.
在△ABF和△MBF 中,
∴△ABF≌△MBF(ASA).
∴MB=AB,AF=MF.
同理可得 NC=AC,AG=NG.
∴FG是△AMN的中位线.
(2)解: 理由如下:
延长AF,AG,分别与直线 BC相交于M,N.
∵BD⊥AF,
∴∠AFB=∠MFB=90°.
在△ABF和△MBF中,
∴△ABF≌△MBF(ASA).
∴MB=AB,AF=MF.同理可得 NC=AC,AG=NG.
∴FG 是△AMN的中位线.
-BC).
基础知识夯实
知识沉淀
1.三角形的中位线定义:连接三角形 叫做三角形的中位线.
2.三角形的中位线定理:三角形的中位线 于第三边,并且等于 .
基础过关
1.如图,在△ABC中,D,E分别是边AB,AC的中点,若 BC=6,则 DE 的长为 ( )
A.2 B.3 C.4 D.6
2.如图,在△MBN中,已知:BM=6,BN=7,MN=10,点A,C,D分别是MB,NB,MN的中点,则四边形ABCD的周长是 .
典型案例探究
知识点 1 三角形中位线的性质
【例题1】如图,M是△ABC 的边BC 的中点,AN 平分∠BAC,BN⊥AN 于点N,延长BN 交AC 于点D,已知 AB=10,AC=16.
(1)求证:BN=DN;
(2)求 MN 的长.
【变式1】如图,等边三角形ABC的边长是2,D,E分别为AB,AC的中点,过点 E 作EF∥CD交BC 的延长线于点 F,连接CD.
(1)求证:DE=CF;
(2)求 EF 的长.
知识点2 三角形中位线的应用
【例题2】已知:如图,在四边形 ABCD 中,对角线AC,BD 相交于点 O,且 AC=BD,E,F分别是AB,CD的中点,EF 分别交 BD,AC于点G,H.求证:OG=OH.
【变式2】如图,已知在四边形ABCD中,AB=DC,E,F分别为AD 与 BC 的中点,连接 EF 与 BA 的延长线相交于点N,与CD的延长线相交于点M.
求证:
课后作业
A 组
1.如图,A,B两点被一座山隔开,M,N分别是AC,BC的中点,测量MN的长度为40m,那么AB的长度为
( )
A.40 m B.80 m
C.160m D.不能确定
2.如图,在△ABC中,点M,N分别是AB,AC的中点,延长 CB至点D,使MN=BD,连接DN,若CD=6,则MN的长为 ( )
A.2 B.3 C.4 D.6
3.若三角形的三条中位线长分别为 2cm ,3cm,4 cm,则原三角形的周长为 ( )
A.4. 5cm B.18cm
C.9 cm D.36 cm
4.在Rt△ABC中,∠C=90°,AC=5,BC=12,则连接两条直角边中点的线段长为 .
5.已知等腰三角形的两条中位线的长分别为 2 和 3,则此等腰三角形的周长为 .
6.如图,在△ABC中,D,E 分别是AB,AC 的中点,△ABC的角平分线AG 交DE 于点F,若∠ABC=70°,∠BAC=54°,求∠AFD的度数.
7.如图, 中,点 D 是AB 的中点,DE∥BC,求证:点 E 是 AC 的中点.
B 组
8.已知在△ABC 中,D 为AB 的中点,E 为AC 上一点,AE=2CE,CD,BE交于O点,OE=2 厘米.求BO 的长.
9.如图,在 中,D 为AC 上一点, F 是AD 的中点,M 为 BC 的中点,连接 MF 并延长交BA 延长线于点E,G 为EF 的中点,求证:AG⊥ME.
C
C 组
10.如图(1),BD,CE 分别是△ABC 的外角平分线,过点 A 作AF⊥BD,AG⊥CE,垂足分别为 F,G,连接FG,延长AF,AG,与直线 BC 相交于M,N.
(1)求证:
(2)如图(2),BD,CE 分别是△ABC 的内角平分线,过点 A 作 AF⊥BD,AG⊥CE,垂足分别为 F,G,连接 FG,则线段 FG 与△ABC 的三边又有怎样的数量关系 请写出你的猜想并说明理由.
第 3 课时 三角形的中位线
【基础知识夯实】
知识沉淀
1.两边中点的线段
2.平行 第三边的一半
基础过关
1. B 2.13
【典型案例探究】
例题1 (1)证明:∵AN平分∠BAC,∴∠1=∠2.
∵BN⊥AN,∴∠ANB=∠AND.
在△ABN和△ADN中,
∴△ABN≌△ADN(ASA).
∴BN=DN.
(2)解:∵△ABN≌△ADN,
∴AD=AB=10,DN=NB.
∴CD=AC-AD=16-10=6.
又∵点 M是BC中点,
∴MN是△BDC的中位线.
变式1 (1)证明:∵D,E 分别为AB,AC的中点,
∵EF∥CD,∴四边形DEFC是平行四边形.
∴DE=CF.
(2)解:∵四边形 DEFC是平行四边形,∴DC=EF.
∵D 为AB 的中点,等边三角形 ABC的边长是 2,
∴BD=AD=1,CD⊥AB,BC=2.
例题2证明:取 BC边的中点M,连接EM,FM,∵M,F分别是BC,CD的中点,
∴MF∥BD,MF=
同理,ME∥AC,ME
∵AC=BD,
∴ME=MF.
∴∠MEF=∠MFE.
∵MF∥BD,∴∠MFE=∠OGH.同理,∠MEF=∠OHG.
∴∠OGH=∠OHG.
∴OG=OH.
变式2证明:如图,连接AC,取AC的中点K,连接 EK,FK,
∵AE=ED,AK=KC,
同理, FK ∥ AB, FK =
=EK.
∴∠FEK=∠EFK.
∵EK∥DC,∴∠CMF=∠FEK.
∵FK∥AB,∴∠BNF=∠EFK.
∴∠BNF=∠CMF.
【课后作业】
1. B 2. A 3. B 4.6.5 5.14或16
6.解:∵∠BAC=54°,AG平分∠BAC,
∴∠BGA=180°-∠ABC-∠BAG=83°.
又∵点D,E分别是AB,AC的中点,∴DE∥BC.
∴∠AFD=∠BGA=83°.
7. 证明: 如图,取 BC 的中点 F,连接 DF.
∵点D 是AB 的中点,
又 DE∥BC,∴四边形 CEDF 是平行四边形.
∴DF=CE.
即点 E 是AC 的中点.
8.解:取 BE的中点 F,连接 DF,如图.
∵D为AB 的中点,
∴ ∠DFO = ∠OEC, ∠OCE=∠ODF.
又∵AE=2EC,∴DF=EC.
∴△DFO≌△CEO.
∴EO=FO.
∵BF=FE,∴BO=3EO=3×2=6厘米.
9.证明:连接BD,取BD的中点为O,连接FO,MO,∵F 是AD 的中点,M为BC的中点,
∴MO是△BCD 的中位线, FO 是△ABD 的中位线.
AB, MO∥AC, OF∥AB.
∵AB=CD,∴MO=FO.∴∠OFM=∠OMF.
∵OF∥AB,∴∠OFM=∠AEF.
∵OM∥AC,∴∠OMF=∠CFM=∠AFE.
∴∠AEF=∠AFE.∴AE=AF.
∵G为EF 的中点,∴AG⊥ME.
10.(1)证明:∵BD⊥AF,∴∠AFB=∠MFB=90°.
在△ABF和△MBF 中,
∴△ABF≌△MBF(ASA).
∴MB=AB,AF=MF.
同理可得 NC=AC,AG=NG.
∴FG是△AMN的中位线.
(2)解: 理由如下:
延长AF,AG,分别与直线 BC相交于M,N.
∵BD⊥AF,
∴∠AFB=∠MFB=90°.
在△ABF和△MBF中,
∴△ABF≌△MBF(ASA).
∴MB=AB,AF=MF.同理可得 NC=AC,AG=NG.
∴FG 是△AMN的中位线.
-BC).
