初中数学人教版八年级下册 第十七章 勾股定理章末整合 感知中考(含答案)
文档属性
| 名称 | 初中数学人教版八年级下册 第十七章 勾股定理章末整合 感知中考(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 538.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-04 09:31:36 | ||
图片预览

文档简介
章末整合·感知中考
知识网络
二、内容归纳
1.勾股定理:直角三角形两条直角边的平方和等于斜边的平方.即在△ABC中,若∠C=90°,则(
2.勾股定理的逆定理:在△ABC中,若( ,则∠C=90°.如果一个三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
3.常用勾股数:①3,4,5;②6,8,10;③5,12,13;④7,24,25;⑤8,15,17.
4.借助几何图形,运用勾股定理,在数轴上表示开不尽方的无理数.
5.互逆命题:如果两个命题的题设和结论正好相反,那么这样的两个命题叫做互逆命题.如果把其中一个叫做原命题,那么另外一个叫做它的逆命题.
6.一般的,如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,称这两个定理互为逆定理.
中考完全接触
考点1 勾股定理的证明
1.勾股定理是“人类最伟大的十个科学发现之一”.我国对勾股定理的证明是由汉代的赵爽在注解《周髀算经》时给出的,他用来证明勾股定理的图案被称为“赵爽弦图”.2002年在北京召开的国际数学大会选它作为会徽.下列图案中是“赵爽弦图”的是 ( )
2公元3世纪初,中国古代数学家赵爽注《周髀算经》时,创造了“赵爽弦图”.如图,设勾a=6,弦c=10,则小正方形ABCD 的面积是 .
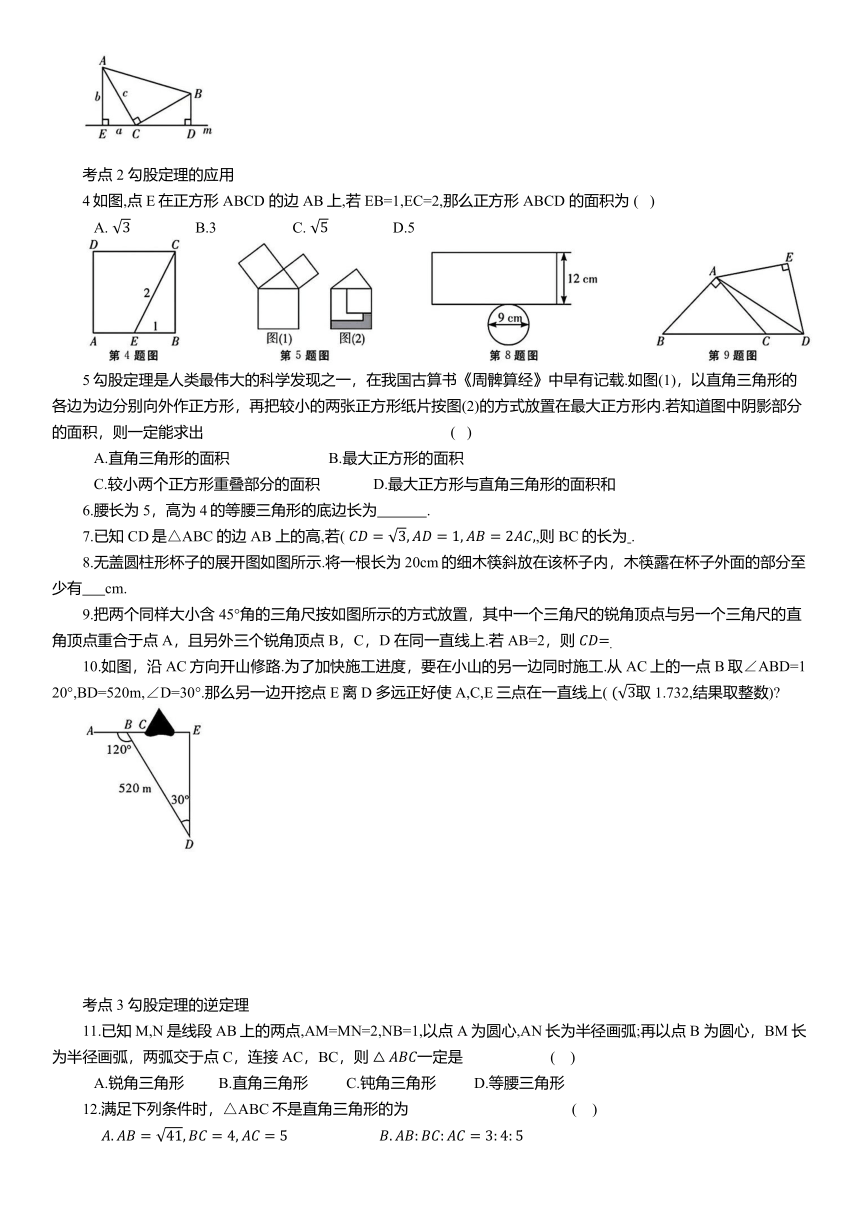
3.如图,等腰直角三角板 ABC 如图放置.直角顶点 C 在直线m 上,分别过点A,B作AE⊥直线m于点E,BD⊥直线m 于点D.
(1)求证:EC=BD;
(2)若设△AEC三边分别为a,b,c,利用此图证明勾股定理.
考点2 勾股定理的应用
4如图,点E在正方形ABCD 的边AB上,若EB=1,EC=2,那么正方形 ABCD 的面积为 ( )
A. B.3 C. D.5
5勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图(1),以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图(2)的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出 ( )
A.直角三角形的面积 B.最大正方形的面积
C.较小两个正方形重叠部分的面积 D.最大正方形与直角三角形的面积和
6.腰长为5,高为4的等腰三角形的底边长为 .
7.已知CD是△ABC的边AB 上的高,若( ,则 BC的长为 .
8.无盖圆柱形杯子的展开图如图所示.将一根长为 20cm的细木筷斜放在该杯子内,木筷露在杯子外面的部分至少有 cm.
9.把两个同样大小含45°角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个三角尺的直角顶点重合于点 A,且另外三个锐角顶点 B,C,D 在同一直线上.若AB=2,则
10.如图,沿AC方向开山修路.为了加快施工进度,要在小山的另一边同时施工.从AC上的一点 B取∠ABD=120°,BD=520m,∠D=30°.那么另一边开挖点E离D 多远正好使A,C,E三点在一直线上( 取1.732,结果取整数)
考点3 勾股定理的逆定理
11.已知M,N是线段AB上的两点,AM=MN=2,NB=1,以点 A为圆心,AN长为半径画弧;再以点 B 为圆心,BM长为半径画弧,两弧交于点 C,连接AC,BC,则 一定是 ( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
12.满足下列条件时,△ABC不是直角三角形的为 ( )
C.∠A:∠B:∠C=3:4:5
13.如图,等边三角形ABC内有一点P,分别连接AP,BP,CP,若 8,CP=10,则
14.如图,在. 中,内角A,B,C所对的边分别为a,b,c.若
求证: 是直角三角形.
C
15.在如图所示的网格中,每个小正方形的边长为1,每个小正方形的顶点叫格点, 的三个顶点均在格点上,以点 A 为圆心,AD长为半径画弧分别交AB,AC于点E,F.
(1)求 三边的长;
(2)求图中由线段EB,BC,CF及 所围成的阴影部分的面积.
章末整合·感知中考
【中考完全接触】
1. B 2.4
3.证明:(1)∵∠ACB=90°,∴∠ACE+∠BCD=90°.
∵AE⊥直线m于点E,∴∠ACE+∠CAE=90°.
∴∠CAE=∠BCD.
在△AEC 与△CDB中,
∴△AEC≌△CDB(AAS).
∴EC=BD.
(2)由(1)得BD=CE=a,CD=AE=b.
又
整理,得
4. B 5. C 6.6 7.2 或2 8.5
提示:过点 A 作 AF⊥BC 于 F,可得 AF= 则 于是 CD=DF-
10.解:∵∠ABD=120°,∠D=30°,
在 Rt△BDE中,BD=520 m,∠D=30°,
∴BE=260 m.
答:另一边开挖点 E离D450 m,正好使A,C,E 三点在一直线上.
11. B 12. C
提示:如图,将△BPC绕点 B 逆时针旋转60°后得△BP'A,连接 PP',根据旋转的性质易得△BPP'为等边三角形,由勾股定理的逆定理得△APP'是直角三角形,则 力形 AP·BP = S△AP·P +
14.证明:
b ].
∴△ABC是直角三角形.
15.解:(1)由勾股定理可得 C
(2)连接AD.
由(1)可知,
∴∠BAC=90°,△ABC是等腰直角三角形.
∴扇形AEF是圆的 .
由勾股定理可得
扇形AEF
=20-5π.
知识网络
二、内容归纳
1.勾股定理:直角三角形两条直角边的平方和等于斜边的平方.即在△ABC中,若∠C=90°,则(
2.勾股定理的逆定理:在△ABC中,若( ,则∠C=90°.如果一个三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
3.常用勾股数:①3,4,5;②6,8,10;③5,12,13;④7,24,25;⑤8,15,17.
4.借助几何图形,运用勾股定理,在数轴上表示开不尽方的无理数.
5.互逆命题:如果两个命题的题设和结论正好相反,那么这样的两个命题叫做互逆命题.如果把其中一个叫做原命题,那么另外一个叫做它的逆命题.
6.一般的,如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,称这两个定理互为逆定理.
中考完全接触
考点1 勾股定理的证明
1.勾股定理是“人类最伟大的十个科学发现之一”.我国对勾股定理的证明是由汉代的赵爽在注解《周髀算经》时给出的,他用来证明勾股定理的图案被称为“赵爽弦图”.2002年在北京召开的国际数学大会选它作为会徽.下列图案中是“赵爽弦图”的是 ( )
2公元3世纪初,中国古代数学家赵爽注《周髀算经》时,创造了“赵爽弦图”.如图,设勾a=6,弦c=10,则小正方形ABCD 的面积是 .
3.如图,等腰直角三角板 ABC 如图放置.直角顶点 C 在直线m 上,分别过点A,B作AE⊥直线m于点E,BD⊥直线m 于点D.
(1)求证:EC=BD;
(2)若设△AEC三边分别为a,b,c,利用此图证明勾股定理.
考点2 勾股定理的应用
4如图,点E在正方形ABCD 的边AB上,若EB=1,EC=2,那么正方形 ABCD 的面积为 ( )
A. B.3 C. D.5
5勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图(1),以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图(2)的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出 ( )
A.直角三角形的面积 B.最大正方形的面积
C.较小两个正方形重叠部分的面积 D.最大正方形与直角三角形的面积和
6.腰长为5,高为4的等腰三角形的底边长为 .
7.已知CD是△ABC的边AB 上的高,若( ,则 BC的长为 .
8.无盖圆柱形杯子的展开图如图所示.将一根长为 20cm的细木筷斜放在该杯子内,木筷露在杯子外面的部分至少有 cm.
9.把两个同样大小含45°角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个三角尺的直角顶点重合于点 A,且另外三个锐角顶点 B,C,D 在同一直线上.若AB=2,则
10.如图,沿AC方向开山修路.为了加快施工进度,要在小山的另一边同时施工.从AC上的一点 B取∠ABD=120°,BD=520m,∠D=30°.那么另一边开挖点E离D 多远正好使A,C,E三点在一直线上( 取1.732,结果取整数)
考点3 勾股定理的逆定理
11.已知M,N是线段AB上的两点,AM=MN=2,NB=1,以点 A为圆心,AN长为半径画弧;再以点 B 为圆心,BM长为半径画弧,两弧交于点 C,连接AC,BC,则 一定是 ( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
12.满足下列条件时,△ABC不是直角三角形的为 ( )
C.∠A:∠B:∠C=3:4:5
13.如图,等边三角形ABC内有一点P,分别连接AP,BP,CP,若 8,CP=10,则
14.如图,在. 中,内角A,B,C所对的边分别为a,b,c.若
求证: 是直角三角形.
C
15.在如图所示的网格中,每个小正方形的边长为1,每个小正方形的顶点叫格点, 的三个顶点均在格点上,以点 A 为圆心,AD长为半径画弧分别交AB,AC于点E,F.
(1)求 三边的长;
(2)求图中由线段EB,BC,CF及 所围成的阴影部分的面积.
章末整合·感知中考
【中考完全接触】
1. B 2.4
3.证明:(1)∵∠ACB=90°,∴∠ACE+∠BCD=90°.
∵AE⊥直线m于点E,∴∠ACE+∠CAE=90°.
∴∠CAE=∠BCD.
在△AEC 与△CDB中,
∴△AEC≌△CDB(AAS).
∴EC=BD.
(2)由(1)得BD=CE=a,CD=AE=b.
又
整理,得
4. B 5. C 6.6 7.2 或2 8.5
提示:过点 A 作 AF⊥BC 于 F,可得 AF= 则 于是 CD=DF-
10.解:∵∠ABD=120°,∠D=30°,
在 Rt△BDE中,BD=520 m,∠D=30°,
∴BE=260 m.
答:另一边开挖点 E离D450 m,正好使A,C,E 三点在一直线上.
11. B 12. C
提示:如图,将△BPC绕点 B 逆时针旋转60°后得△BP'A,连接 PP',根据旋转的性质易得△BPP'为等边三角形,由勾股定理的逆定理得△APP'是直角三角形,则 力形 AP·BP = S△AP·P +
14.证明:
b ].
∴△ABC是直角三角形.
15.解:(1)由勾股定理可得 C
(2)连接AD.
由(1)可知,
∴∠BAC=90°,△ABC是等腰直角三角形.
∴扇形AEF是圆的 .
由勾股定理可得
扇形AEF
=20-5π.
