初中数学人教版八年级下册17.2 (第2课时 )勾股定理的逆定理(二)——应用同步(分层)练习【基础知识夯实】(含答案)
文档属性
| 名称 | 初中数学人教版八年级下册17.2 (第2课时 )勾股定理的逆定理(二)——应用同步(分层)练习【基础知识夯实】(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 428.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-04 09:36:03 | ||
图片预览


文档简介
17.2 勾股定理的逆定理
第 2课时 勾股定理的逆定理(二)—— 应用
基础知识夯实
知识沉淀
1.勾股定理的逆定理的应用,实质是由数量关系决定位置关系,应用勾股定理的逆定理抽象出数学方程模型或者进行图形的转化,是判断三角形的形状、计算图形的面积问题的一种行之有效的方法.
2.方向角:如图,OA 是 60°,OB 是东南方向,OC 是正东方向,OD 是南偏西 .
基础过关
1.小丽和小芳二人同时从公园去图书馆,都是每分钟走 50米,小丽走直线用了 10 分钟,小芳先回家拿了钱再去图书馆,小芳从公园回家用了6分钟,从家到图书馆用了8分钟,小芳从公园到图书馆拐了个( )
A.锐角 B.直角
C.钝角 D.不能确定
2.小明向东走80 m后,沿另一方向又走了 60 m,再沿第三个方向走 100m回到原地.则小明向东走了80 m 后又向 走了 60 m.
典型案例探究
知识点 勾股定理逆定理的应用
【例题】如图,甲船以5海里/时的速度离开港口 O沿南偏东30°方向航行,乙船同时同地沿某方向以12 海里/时的速度航行,已知它们离开港口 2 小时后分别到达B,A两点,且AB=26海里,你能知道乙船是沿哪个方向航行的吗
【变式】如图,C地到A,B两地分别有笔直的道路CA,CB 相连,A 地与B 地之间有一条河流通过,A,B,C三地的距离如图所示.
(1)如果 A 地在C 地的正东方向,那么 B 地在 C 地的什么方向
(2)现计划把河水从河道AB段的点 D 引到C地,求 C,D两地间的最短距离.
课后作业
A 组
1.满足下列条件的△ABC,不是直角三角形的是( )
B. a:b:c=3:4:5
C.∠A:∠B:∠C=9:12: 15
D.∠C=∠A-∠B
2.给出下列几组数:①4,5,6;②8,15,16;③n -1,2n,n +1(n>1);④m -n ,2mn,m +n (m>n>0).其中一定能组成直角三角形三边长的是 ( )
A.①② B.③④
C.①③④ D.④
3.在△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,下列结论中不正确的是 ( )
A.如果∠A-∠B=∠C,那么△ABC是直角三角形
B.如果 ,那么△ABC是直角三角形且∠C=90°
C.如果∠A:∠B:∠C=1: 3: 2,那么△ABC 是直角三角形
D.如果 ,那么△ABC是直角三角形
4.如果三角形的三边长分别为5,m,n,且(m+n)(m—n)=25,那么此三角形形状为 ( )
A.锐角三角形 B.钝角三角形
C.等腰直角三角形 D.直角三角形
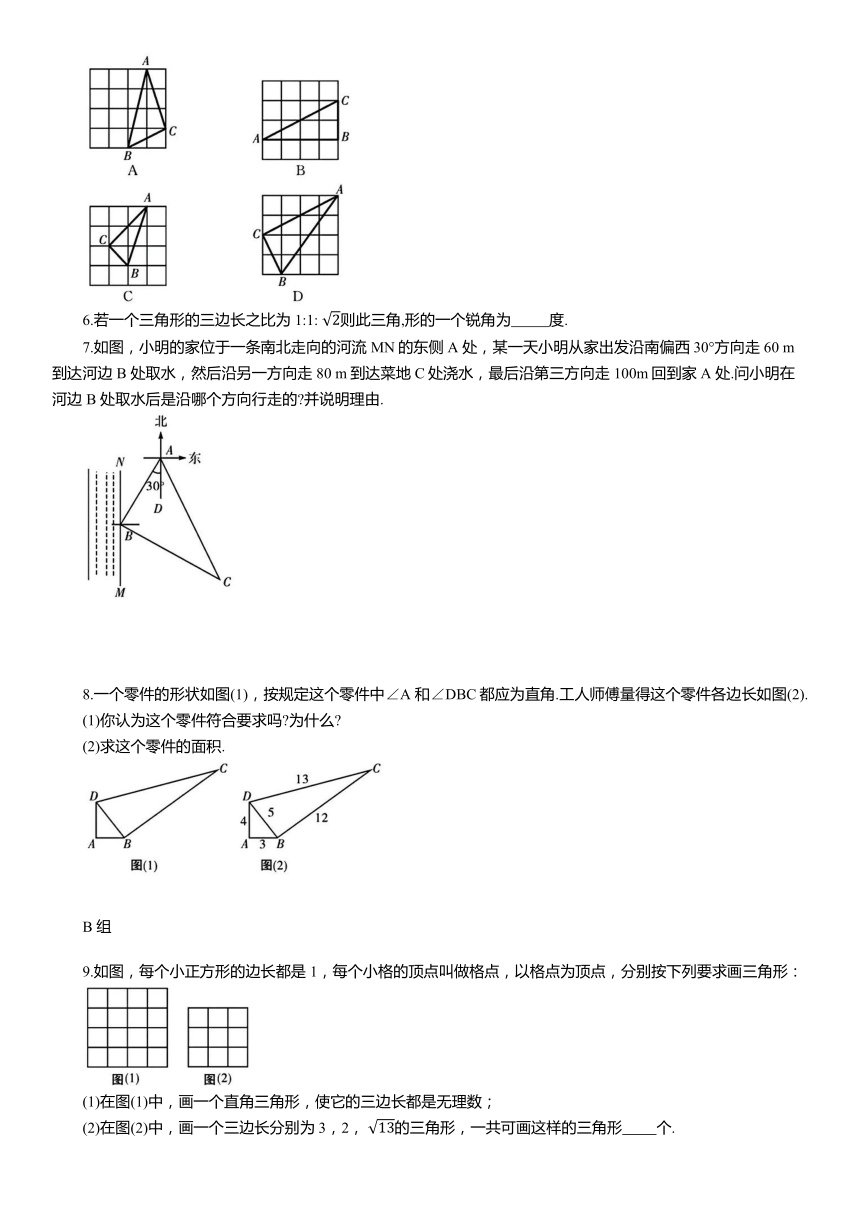
5.如图,在四个均由十六个小正方形组成的正方形网格中,各有一个三角形ABC,那么这四个三角形中,不是直角三角形的是 ( )
6.若一个三角形的三边长之比为1:1: 则此三角,形的一个锐角为 度.
7.如图,小明的家位于一条南北走向的河流 MN的东侧A 处,某一天小明从家出发沿南偏西30°方向走60 m到达河边 B 处取水,然后沿另一方向走 80 m到达菜地 C处浇水,最后沿第三方向走 100m回到家A 处.问小明在河边 B 处取水后是沿哪个方向行走的 并说明理由.
8.一个零件的形状如图(1),按规定这个零件中∠A 和∠DBC都应为直角.工人师傅量得这个零件各边长如图(2).
(1)你认为这个零件符合要求吗 为什么
(2)求这个零件的面积.
B 组
9.如图,每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点,分别按下列要求画三角形:
(1)在图(1)中,画一个直角三角形,使它的三边长都是无理数;
(2)在图(2)中,画一个三边长分别为3,2, 的三角形,一共可画这样的三角形 个.
10.如图,在△ABC中,AB=4,AC=3,DE 是BC 的垂直平分线,交 BC 于点 D,交 AB 于点 E,AF⊥BC于点 F.
(1)若∠BAC=90°,求AE的长;
(2)若 DF=0.7,求证:△ABC为直角三角形.
C 组
11.设a,b,c是一个三角形的三条边的长,且a 是最长边,我们可以利用a,b,c 三边长间的关系来判断这个三角形的形状:①若 则该三角形是直角三角形;②若( 则该三角形是钝角三角形; 则该三角形是锐角三角形.例如一个三角形的三边长分别是4,5,6,则最长边是6,由于 故由上面③可知该三角形是锐角三角形,请解答以下问题:
(1)若一个三角形的三条边长分别是2,3,4,则该三角形是 三角形;
(2)若一个三角形的三条边长分别是3,6,x,且这个三角形是直角三角形,求x的值;
(3)若一个三角形的三条边长 其中a 是最长边,请判断这个三角形的形状,并写出你的判断过程.
第2课时 勾股定理的逆定理(二)——应用【基础知识夯实】
知识沉淀
2.北偏东 20°
基础过关
1. B 2.北或南
【典型案例探究】
例题 解:由题意可知,OB=5×2=10(海里),OA=12×2=24(海里),AB=26海里,
即
∴△OAB是直角三角形.
∵∠BOD=30°,
故乙船是沿南偏西 60°方向航行的.
变式 解:
∴△ABC是直角三角形,∠ACB=90°.
∵A 地在C 地的正东方向,
∴B地在C 地的正北方向.
(2)过点C作AB的垂线,当垂足为点 D时,C,D两地间的距离最短.
∵△ABC是直角三角形,
则C,D两地间的最短距离是 4.8km.
【课后作业】
1. C 2. B 3. B 4. D 5. A 6.45
7.解:∵AB=60,BC=80,AC=100,
∴AB +BC =AC .∴∠ABC=90°.
∴AD∥NM.∴∠NBA=∠BAD=30°.
∴小明在河边 B 处取水后是沿南偏东 60°方向行走的.
8.解:(1)∵AD=4,AB=3,BD=5,DC=13,BC=12,
∴AB +AD =BD ,BD +BC =DC .
∴△ABD,△BDC是直角三角形,∠A=90°,∠DBC=90°.
故这个零件符合要求.
(2)这个零件的面积=△ABD的面积+△BDC的面积=3×4÷2+5×12÷2=6+30=36.
故这个零件的面积是36.
9.解:(1)△ABC 即为所求,如图(1).
如图(2),一共(1)画这样的三角形(2)6个.
10.(1)解: 连接 CE,设 AE=x,
∵AB=4,∴BE=4-x.
∵DE 是 BC 的垂 直平分线,
∴CE=BE=4-x.
∵∠BAC=90°,AC=3,
即
(2)证明:设BD=y,则CD=y,
∵DF=0.7,∴BF=y+0.7,CF=y-0.7.
.
∴y=2.5.
∴△ABC为直角三角形.
11.解:(1)钝角
(2)若x是最长边,则
若6是最长边,则.
故 x的值为3 或.
(3)因为
所以
则这个三角形的形状是钝角三角形.
第 2课时 勾股定理的逆定理(二)—— 应用
基础知识夯实
知识沉淀
1.勾股定理的逆定理的应用,实质是由数量关系决定位置关系,应用勾股定理的逆定理抽象出数学方程模型或者进行图形的转化,是判断三角形的形状、计算图形的面积问题的一种行之有效的方法.
2.方向角:如图,OA 是 60°,OB 是东南方向,OC 是正东方向,OD 是南偏西 .
基础过关
1.小丽和小芳二人同时从公园去图书馆,都是每分钟走 50米,小丽走直线用了 10 分钟,小芳先回家拿了钱再去图书馆,小芳从公园回家用了6分钟,从家到图书馆用了8分钟,小芳从公园到图书馆拐了个( )
A.锐角 B.直角
C.钝角 D.不能确定
2.小明向东走80 m后,沿另一方向又走了 60 m,再沿第三个方向走 100m回到原地.则小明向东走了80 m 后又向 走了 60 m.
典型案例探究
知识点 勾股定理逆定理的应用
【例题】如图,甲船以5海里/时的速度离开港口 O沿南偏东30°方向航行,乙船同时同地沿某方向以12 海里/时的速度航行,已知它们离开港口 2 小时后分别到达B,A两点,且AB=26海里,你能知道乙船是沿哪个方向航行的吗
【变式】如图,C地到A,B两地分别有笔直的道路CA,CB 相连,A 地与B 地之间有一条河流通过,A,B,C三地的距离如图所示.
(1)如果 A 地在C 地的正东方向,那么 B 地在 C 地的什么方向
(2)现计划把河水从河道AB段的点 D 引到C地,求 C,D两地间的最短距离.
课后作业
A 组
1.满足下列条件的△ABC,不是直角三角形的是( )
B. a:b:c=3:4:5
C.∠A:∠B:∠C=9:12: 15
D.∠C=∠A-∠B
2.给出下列几组数:①4,5,6;②8,15,16;③n -1,2n,n +1(n>1);④m -n ,2mn,m +n (m>n>0).其中一定能组成直角三角形三边长的是 ( )
A.①② B.③④
C.①③④ D.④
3.在△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,下列结论中不正确的是 ( )
A.如果∠A-∠B=∠C,那么△ABC是直角三角形
B.如果 ,那么△ABC是直角三角形且∠C=90°
C.如果∠A:∠B:∠C=1: 3: 2,那么△ABC 是直角三角形
D.如果 ,那么△ABC是直角三角形
4.如果三角形的三边长分别为5,m,n,且(m+n)(m—n)=25,那么此三角形形状为 ( )
A.锐角三角形 B.钝角三角形
C.等腰直角三角形 D.直角三角形
5.如图,在四个均由十六个小正方形组成的正方形网格中,各有一个三角形ABC,那么这四个三角形中,不是直角三角形的是 ( )
6.若一个三角形的三边长之比为1:1: 则此三角,形的一个锐角为 度.
7.如图,小明的家位于一条南北走向的河流 MN的东侧A 处,某一天小明从家出发沿南偏西30°方向走60 m到达河边 B 处取水,然后沿另一方向走 80 m到达菜地 C处浇水,最后沿第三方向走 100m回到家A 处.问小明在河边 B 处取水后是沿哪个方向行走的 并说明理由.
8.一个零件的形状如图(1),按规定这个零件中∠A 和∠DBC都应为直角.工人师傅量得这个零件各边长如图(2).
(1)你认为这个零件符合要求吗 为什么
(2)求这个零件的面积.
B 组
9.如图,每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点,分别按下列要求画三角形:
(1)在图(1)中,画一个直角三角形,使它的三边长都是无理数;
(2)在图(2)中,画一个三边长分别为3,2, 的三角形,一共可画这样的三角形 个.
10.如图,在△ABC中,AB=4,AC=3,DE 是BC 的垂直平分线,交 BC 于点 D,交 AB 于点 E,AF⊥BC于点 F.
(1)若∠BAC=90°,求AE的长;
(2)若 DF=0.7,求证:△ABC为直角三角形.
C 组
11.设a,b,c是一个三角形的三条边的长,且a 是最长边,我们可以利用a,b,c 三边长间的关系来判断这个三角形的形状:①若 则该三角形是直角三角形;②若( 则该三角形是钝角三角形; 则该三角形是锐角三角形.例如一个三角形的三边长分别是4,5,6,则最长边是6,由于 故由上面③可知该三角形是锐角三角形,请解答以下问题:
(1)若一个三角形的三条边长分别是2,3,4,则该三角形是 三角形;
(2)若一个三角形的三条边长分别是3,6,x,且这个三角形是直角三角形,求x的值;
(3)若一个三角形的三条边长 其中a 是最长边,请判断这个三角形的形状,并写出你的判断过程.
第2课时 勾股定理的逆定理(二)——应用【基础知识夯实】
知识沉淀
2.北偏东 20°
基础过关
1. B 2.北或南
【典型案例探究】
例题 解:由题意可知,OB=5×2=10(海里),OA=12×2=24(海里),AB=26海里,
即
∴△OAB是直角三角形.
∵∠BOD=30°,
故乙船是沿南偏西 60°方向航行的.
变式 解:
∴△ABC是直角三角形,∠ACB=90°.
∵A 地在C 地的正东方向,
∴B地在C 地的正北方向.
(2)过点C作AB的垂线,当垂足为点 D时,C,D两地间的距离最短.
∵△ABC是直角三角形,
则C,D两地间的最短距离是 4.8km.
【课后作业】
1. C 2. B 3. B 4. D 5. A 6.45
7.解:∵AB=60,BC=80,AC=100,
∴AB +BC =AC .∴∠ABC=90°.
∴AD∥NM.∴∠NBA=∠BAD=30°.
∴小明在河边 B 处取水后是沿南偏东 60°方向行走的.
8.解:(1)∵AD=4,AB=3,BD=5,DC=13,BC=12,
∴AB +AD =BD ,BD +BC =DC .
∴△ABD,△BDC是直角三角形,∠A=90°,∠DBC=90°.
故这个零件符合要求.
(2)这个零件的面积=△ABD的面积+△BDC的面积=3×4÷2+5×12÷2=6+30=36.
故这个零件的面积是36.
9.解:(1)△ABC 即为所求,如图(1).
如图(2),一共(1)画这样的三角形(2)6个.
10.(1)解: 连接 CE,设 AE=x,
∵AB=4,∴BE=4-x.
∵DE 是 BC 的垂 直平分线,
∴CE=BE=4-x.
∵∠BAC=90°,AC=3,
即
(2)证明:设BD=y,则CD=y,
∵DF=0.7,∴BF=y+0.7,CF=y-0.7.
.
∴y=2.5.
∴△ABC为直角三角形.
11.解:(1)钝角
(2)若x是最长边,则
若6是最长边,则.
故 x的值为3 或.
(3)因为
所以
则这个三角形的形状是钝角三角形.
