初中数学人教版八年级下册20.2 数据的波动程度同步(分层)练习(含答案)
文档属性
| 名称 | 初中数学人教版八年级下册20.2 数据的波动程度同步(分层)练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 607.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-04 11:04:33 | ||
图片预览


文档简介
20.2 数据的波动程度
基础知识夯实
知识沉淀
1.方差:一组数据.x ,x ,x ,…,x 的方差计算公式:s = .
2.方差的意义:反映数据波动的大小,方差越大,波动越 ;方差越小,波动越 .
基础过关
1.在一次中学生汉字听写大赛中,某中学代表队6名同学的笔试成绩分别为75,85,91,85,95,85.关于这6名学生成绩,下列说法正确的是 ( )
A.平均数是87 B.中位数是88
C.众数是85 D.方差是230
2.某同学对甲、乙、丙、丁四个市场二月份每天的白菜价格进行调查,计算后发现这个月四个市场的价格平均值相同、方差分别为 10.1,s r =7.4,二月份白菜价格最稳定的市场是 .
典型案例探究
知识点 1方差
【例题1】一组数据2,0,1,x,3的平均数是2,则这组数据的方差是 ( )
A.2 B.4
C.1 D.3
【变式1】已知一组数据为2,3,5,7,8,则这组数据的方差为 ( )
A.3 B.4.5
C.5.2 D.6
知识点 2 方差的意义
【例题2】甲、乙、丙、丁四人进行射击测试,每人10次射击成绩平均数都是 8.8环,方差分别为 环 , 环 , 环 , 环 ,则四人中成绩最稳定的是 ( )
A.甲 B.乙
C.丙 D.丁
【变式2】 甲,乙,丙,丁四名同学在学校演讲选拔赛的成绩平均数x与方差s 如下表所示:
甲 乙 丙 丁
平均数 8.0 8.0 8.5 8.5
方差 s 3.5 15.5 3.5 16.5
根据表中数据,要从中选一名成绩好又发挥稳定的同学参加市演讲比赛,应该选择 ( )
A.甲 B.乙 C.丙 D.丁
知识点3 方差的综合运用
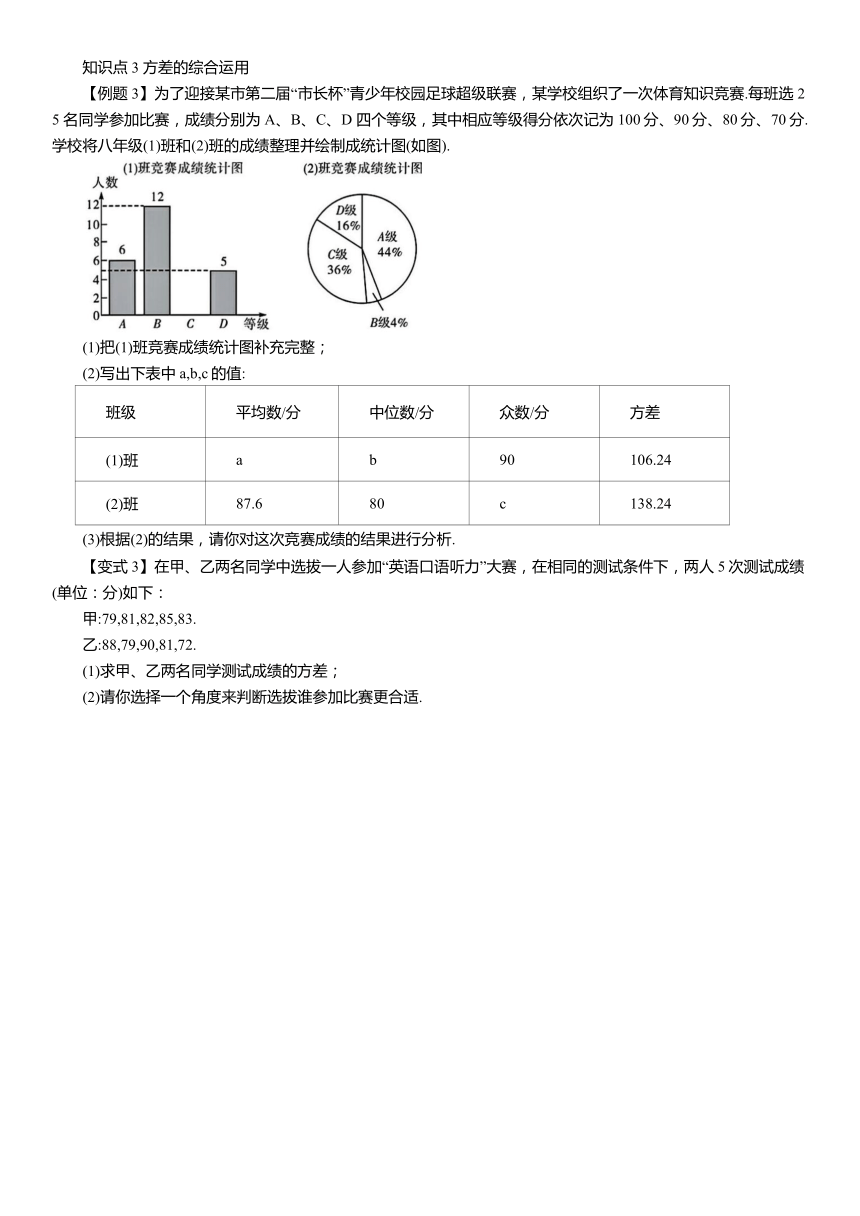
【例题3】为了迎接某市第二届“市长杯”青少年校园足球超级联赛,某学校组织了一次体育知识竞赛.每班选25 名同学参加比赛,成绩分别为 A、B、C、D 四个等级,其中相应等级得分依次记为100分、90分、80分、70分.学校将八年级(1)班和(2)班的成绩整理并绘制成统计图(如图).
(1)把(1)班竞赛成绩统计图补充完整;
(2)写出下表中a,b,c的值:
班级 平均数/分 中位数/分 众数/分 方差
(1)班 a b 90 106.24
(2)班 87.6 80 c 138.24
(3)根据(2)的结果,请你对这次竞赛成绩的结果进行分析.
【变式3】在甲、乙两名同学中选拔一人参加“英语口语听力”大赛,在相同的测试条件下,两人5次测试成绩(单位:分)如下:
甲:79,81,82,85,83.
乙:88,79,90,81,72.
(1)求甲、乙两名同学测试成绩的方差;
(2)请你选择一个角度来判断选拔谁参加比赛更合适.
课后作业
A 组
1.数据-1,0,1,2,3的方差是 ( )
A.10 B.2
C. D.1
2.立定跳远是小刚同学体育中考的选考项目之一.某次体育课上,体育老师记录了小刚的一组立定跳远训练成绩如下表:
成绩/m 2.35 2.4 2.45 2.5 2.55
次数 1 1 2 5 1
则下列关于这组数据的说法中正确的是 ( )
A.众数是2.45 B.平均数是2.45
C.中位数是2.5 D.方差是0.48
3.某科普小组有 5 名成员,身高分别为(单位:cm):160,165,170,163,167.增加1名身高为 165 cm的成员后,现科普小组成员的身高与原来相比,下列说法正确的是 ( )
A.平均数和中位数不变,方差变小
B.平均数和中位数不变,方差变大
C.平均数不变,中位数和方差变小
D.平均数变小,中位数和方差不变
4.有一组数据:3,a,4,6,7,它们的平均数是5,则a= ,这组数据的方差是 .
5.下面是甲、乙两人10次射击成绩(环数)的条形统计图,则这两人 10次射击命中环数的方差su- s .(填“>”“<”或“=”)
6.在一次广场舞比赛中,甲、乙两个队参加表演的女演员的身高(单位:cm)分别是:
甲队 163 164 165 165 165 165 166 167
乙队 162 164 164 165 165 166 167 167
(1)求甲队女演员身高的平均数、中位数、众数;
(2)哪个队女演员的身高更整齐 请从方差的角度说明理由.
B 组
7.甲、乙两名同学进入八年级后,某科6次考试成绩如图所示:
(1)请根据统计图填写下表:
平均数 方差 中位数 众数
甲 75 75
乙 33.3 72.5
(2)请你分别从以下两个不同的方面对甲、乙两名同学 6次考试成绩进行分析,你认为反映出什么问题
①从平均数和方差相结合分析;
②从折线图上两名同学分数的走势上分析.
8.近几年,随着钓鱼岛事件、南海危机、萨德入韩等一系列事件的发生,我们国家的安全一再受到威胁,所谓“国家兴亡,匹夫有责”,某校积极开展国防知识教育,九年级甲、乙两班分别选5名同学参加“国防知识”比赛,其预赛成绩如图所示:
(1)根据右下图填写下表:
班级 平均数 中位数 众数 方差
甲班 8.5
乙班 8.5 10 1.6
(2)根据上表数据,分别从平均数、中位数、众数、方差的角度对甲乙两班进行分析.
C 组
9.某校要在两个体育特长生小明、小勇中挑选一人参加市跳远比赛,在跳远专项测试及之后的 7 次跳远选拔赛中,他们的成绩如下表所示(单位:cm):
姓名 一专项测试和7次选拔赛成绩
小明 603 589 602 596 604 612 608
小勇 597 580 597 630 590 631 596
(1)分别求出他们成绩的中位数、平均数及方差;
(2)你发现小明、小勇的成绩各有什么特点
(3)经查阅比赛资料,成绩若达到6.00 m,就很可能夺得冠军,你认为选谁参赛更有把握
(4)以往的该项最好成绩纪录是6.15m,为了打破纪录,你认为应选谁去参赛
20.2 数据的波动程度
【基础知识夯实】
知识沉淀
2.大 小
基础过关
1. C 2.乙
【典型案例探究】
例题1 A 变式1 C 例题 2 B 变式2 C
例题3 解:(1)(1)班中C级的有 25-6-12-5=2人,补图如下:
(1)班竞赛成绩统计图
(2)a=87.6,b=90,c=100
(3)①从平均数和中位数的角度,(1)班和(2)班平均数相等,(1)班的中位数大于(2)班的中位数,故(1)班成绩好于(2)班;
②从平均数和众数的角度,(1)班和(2)班平均数相等,(1)班的众数小于(2)班的众数,故(2)班成绩好于(1)班;
③从 B级以上(包括B级)的人数的角度,(1)班有 18 人,(2)班有 12 人,故(1)班成绩好于(2)班.
变式3 解: (分),
(分),
(2)选拔甲参加比赛更合适,因为甲的方差较小,成绩比较稳定.
【课后作业】
1. B 2. C 3. A 4.5 2 5.>
6.解:(1)平均数是 165 cm,中位数是 165 cm,众数是165 cm.
(2)甲队女演员的身高更整齐,理由如下:
乙队女演员的身高平均数 +165+166+167+167)=165(cm),
将两组数据各减去 165 得:-2,-1,0,0,0,0,1,2;-3,-1,-1,0,0,1,2,2.
甲组数据方差 乙组方差 ∴甲队女演员的身高更整齐.
7.解(1)甲方差:
甲的中位数为75,
乙的平均数为 (85+70+70+75+70+80)=75.
乙的众数为70.
故答案为:125,75,75,70.
(2)①从平均数看,甲同学的成绩比乙同学稍好,但是从方差看,乙同学的方差小,乙同学成绩稳定,综合平均数和方差分析,乙同学总体成绩比甲同学好;
②从折线图上两名同学分数的走势,甲同学的成绩在稳步直线上升,属于进步计较快,乙同学的成绩有较大幅度波动,不算稳定.
8.解:(1)8.5 8.5 0.7 8
(2)从平均数看,两班平均数相同,则甲、乙两班的成绩一样高;从中位数看,甲班的中位数大,所以甲班的成绩较好;从众数看,乙班的众数大,所以乙班的成绩较好;从方差看,甲班的方差小,所以甲班的成绩更稳定.
9.解:(1)将小勇成绩从小到大依次排列为580,590,596,597,597,630,631,中位数为597 cm,
将小明成绩从小到大依次排列为589,596,602,603,604,608,612,中位数为 603 cm,
小明成绩的平均数为:(589+596+602+603+604+608+612)÷7=602cm,
小勇成绩的平均数为:(580+590+596+597+597+630+631)÷7=603cm,
方差为:
(2)从成绩的中位数来看,小明较高成绩的次数比小勇的多;从成绩的平均数来看,小勇成绩的“平均水平”比小明的高,从成绩的方差来看,小明的成绩比小勇的稳定.
(3)在跳远专项测试以及之后的7 次跳远选拔赛中,小明有5次成绩超过6米,而小勇只有两次超过6米,从成绩的方差来看,小明的成绩比小勇的稳定,选小明更有把握夺冠.
(4)小勇有两次成绩为 6.30米和6.31米,超过6.15米,而小明没有一次达到6.15米,故选小勇.
基础知识夯实
知识沉淀
1.方差:一组数据.x ,x ,x ,…,x 的方差计算公式:s = .
2.方差的意义:反映数据波动的大小,方差越大,波动越 ;方差越小,波动越 .
基础过关
1.在一次中学生汉字听写大赛中,某中学代表队6名同学的笔试成绩分别为75,85,91,85,95,85.关于这6名学生成绩,下列说法正确的是 ( )
A.平均数是87 B.中位数是88
C.众数是85 D.方差是230
2.某同学对甲、乙、丙、丁四个市场二月份每天的白菜价格进行调查,计算后发现这个月四个市场的价格平均值相同、方差分别为 10.1,s r =7.4,二月份白菜价格最稳定的市场是 .
典型案例探究
知识点 1方差
【例题1】一组数据2,0,1,x,3的平均数是2,则这组数据的方差是 ( )
A.2 B.4
C.1 D.3
【变式1】已知一组数据为2,3,5,7,8,则这组数据的方差为 ( )
A.3 B.4.5
C.5.2 D.6
知识点 2 方差的意义
【例题2】甲、乙、丙、丁四人进行射击测试,每人10次射击成绩平均数都是 8.8环,方差分别为 环 , 环 , 环 , 环 ,则四人中成绩最稳定的是 ( )
A.甲 B.乙
C.丙 D.丁
【变式2】 甲,乙,丙,丁四名同学在学校演讲选拔赛的成绩平均数x与方差s 如下表所示:
甲 乙 丙 丁
平均数 8.0 8.0 8.5 8.5
方差 s 3.5 15.5 3.5 16.5
根据表中数据,要从中选一名成绩好又发挥稳定的同学参加市演讲比赛,应该选择 ( )
A.甲 B.乙 C.丙 D.丁
知识点3 方差的综合运用
【例题3】为了迎接某市第二届“市长杯”青少年校园足球超级联赛,某学校组织了一次体育知识竞赛.每班选25 名同学参加比赛,成绩分别为 A、B、C、D 四个等级,其中相应等级得分依次记为100分、90分、80分、70分.学校将八年级(1)班和(2)班的成绩整理并绘制成统计图(如图).
(1)把(1)班竞赛成绩统计图补充完整;
(2)写出下表中a,b,c的值:
班级 平均数/分 中位数/分 众数/分 方差
(1)班 a b 90 106.24
(2)班 87.6 80 c 138.24
(3)根据(2)的结果,请你对这次竞赛成绩的结果进行分析.
【变式3】在甲、乙两名同学中选拔一人参加“英语口语听力”大赛,在相同的测试条件下,两人5次测试成绩(单位:分)如下:
甲:79,81,82,85,83.
乙:88,79,90,81,72.
(1)求甲、乙两名同学测试成绩的方差;
(2)请你选择一个角度来判断选拔谁参加比赛更合适.
课后作业
A 组
1.数据-1,0,1,2,3的方差是 ( )
A.10 B.2
C. D.1
2.立定跳远是小刚同学体育中考的选考项目之一.某次体育课上,体育老师记录了小刚的一组立定跳远训练成绩如下表:
成绩/m 2.35 2.4 2.45 2.5 2.55
次数 1 1 2 5 1
则下列关于这组数据的说法中正确的是 ( )
A.众数是2.45 B.平均数是2.45
C.中位数是2.5 D.方差是0.48
3.某科普小组有 5 名成员,身高分别为(单位:cm):160,165,170,163,167.增加1名身高为 165 cm的成员后,现科普小组成员的身高与原来相比,下列说法正确的是 ( )
A.平均数和中位数不变,方差变小
B.平均数和中位数不变,方差变大
C.平均数不变,中位数和方差变小
D.平均数变小,中位数和方差不变
4.有一组数据:3,a,4,6,7,它们的平均数是5,则a= ,这组数据的方差是 .
5.下面是甲、乙两人10次射击成绩(环数)的条形统计图,则这两人 10次射击命中环数的方差su- s .(填“>”“<”或“=”)
6.在一次广场舞比赛中,甲、乙两个队参加表演的女演员的身高(单位:cm)分别是:
甲队 163 164 165 165 165 165 166 167
乙队 162 164 164 165 165 166 167 167
(1)求甲队女演员身高的平均数、中位数、众数;
(2)哪个队女演员的身高更整齐 请从方差的角度说明理由.
B 组
7.甲、乙两名同学进入八年级后,某科6次考试成绩如图所示:
(1)请根据统计图填写下表:
平均数 方差 中位数 众数
甲 75 75
乙 33.3 72.5
(2)请你分别从以下两个不同的方面对甲、乙两名同学 6次考试成绩进行分析,你认为反映出什么问题
①从平均数和方差相结合分析;
②从折线图上两名同学分数的走势上分析.
8.近几年,随着钓鱼岛事件、南海危机、萨德入韩等一系列事件的发生,我们国家的安全一再受到威胁,所谓“国家兴亡,匹夫有责”,某校积极开展国防知识教育,九年级甲、乙两班分别选5名同学参加“国防知识”比赛,其预赛成绩如图所示:
(1)根据右下图填写下表:
班级 平均数 中位数 众数 方差
甲班 8.5
乙班 8.5 10 1.6
(2)根据上表数据,分别从平均数、中位数、众数、方差的角度对甲乙两班进行分析.
C 组
9.某校要在两个体育特长生小明、小勇中挑选一人参加市跳远比赛,在跳远专项测试及之后的 7 次跳远选拔赛中,他们的成绩如下表所示(单位:cm):
姓名 一专项测试和7次选拔赛成绩
小明 603 589 602 596 604 612 608
小勇 597 580 597 630 590 631 596
(1)分别求出他们成绩的中位数、平均数及方差;
(2)你发现小明、小勇的成绩各有什么特点
(3)经查阅比赛资料,成绩若达到6.00 m,就很可能夺得冠军,你认为选谁参赛更有把握
(4)以往的该项最好成绩纪录是6.15m,为了打破纪录,你认为应选谁去参赛
20.2 数据的波动程度
【基础知识夯实】
知识沉淀
2.大 小
基础过关
1. C 2.乙
【典型案例探究】
例题1 A 变式1 C 例题 2 B 变式2 C
例题3 解:(1)(1)班中C级的有 25-6-12-5=2人,补图如下:
(1)班竞赛成绩统计图
(2)a=87.6,b=90,c=100
(3)①从平均数和中位数的角度,(1)班和(2)班平均数相等,(1)班的中位数大于(2)班的中位数,故(1)班成绩好于(2)班;
②从平均数和众数的角度,(1)班和(2)班平均数相等,(1)班的众数小于(2)班的众数,故(2)班成绩好于(1)班;
③从 B级以上(包括B级)的人数的角度,(1)班有 18 人,(2)班有 12 人,故(1)班成绩好于(2)班.
变式3 解: (分),
(分),
(2)选拔甲参加比赛更合适,因为甲的方差较小,成绩比较稳定.
【课后作业】
1. B 2. C 3. A 4.5 2 5.>
6.解:(1)平均数是 165 cm,中位数是 165 cm,众数是165 cm.
(2)甲队女演员的身高更整齐,理由如下:
乙队女演员的身高平均数 +165+166+167+167)=165(cm),
将两组数据各减去 165 得:-2,-1,0,0,0,0,1,2;-3,-1,-1,0,0,1,2,2.
甲组数据方差 乙组方差 ∴甲队女演员的身高更整齐.
7.解(1)甲方差:
甲的中位数为75,
乙的平均数为 (85+70+70+75+70+80)=75.
乙的众数为70.
故答案为:125,75,75,70.
(2)①从平均数看,甲同学的成绩比乙同学稍好,但是从方差看,乙同学的方差小,乙同学成绩稳定,综合平均数和方差分析,乙同学总体成绩比甲同学好;
②从折线图上两名同学分数的走势,甲同学的成绩在稳步直线上升,属于进步计较快,乙同学的成绩有较大幅度波动,不算稳定.
8.解:(1)8.5 8.5 0.7 8
(2)从平均数看,两班平均数相同,则甲、乙两班的成绩一样高;从中位数看,甲班的中位数大,所以甲班的成绩较好;从众数看,乙班的众数大,所以乙班的成绩较好;从方差看,甲班的方差小,所以甲班的成绩更稳定.
9.解:(1)将小勇成绩从小到大依次排列为580,590,596,597,597,630,631,中位数为597 cm,
将小明成绩从小到大依次排列为589,596,602,603,604,608,612,中位数为 603 cm,
小明成绩的平均数为:(589+596+602+603+604+608+612)÷7=602cm,
小勇成绩的平均数为:(580+590+596+597+597+630+631)÷7=603cm,
方差为:
(2)从成绩的中位数来看,小明较高成绩的次数比小勇的多;从成绩的平均数来看,小勇成绩的“平均水平”比小明的高,从成绩的方差来看,小明的成绩比小勇的稳定.
(3)在跳远专项测试以及之后的7 次跳远选拔赛中,小明有5次成绩超过6米,而小勇只有两次超过6米,从成绩的方差来看,小明的成绩比小勇的稳定,选小明更有把握夺冠.
(4)小勇有两次成绩为 6.30米和6.31米,超过6.15米,而小明没有一次达到6.15米,故选小勇.
