2024年广东省中考数学真题(含答案)
文档属性
| 名称 | 2024年广东省中考数学真题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 462.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-03 13:50:15 | ||
图片预览



文档简介
2024年广东省中考数学试卷
一、选择题:本大题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.计算﹣5+3的结果是( )
A.﹣2 B.﹣8 C.2 D.8
2.下列几何图形中,既是中心对称图形也是轴对称图形的是( )
A. B. C. D.
3.2024年6月6日,嫦娥六号在距离地球约384000千米外上演“太空牵手”,完成月球轨道的交会对接.数据384000用科学记数法表示为( )
A.3.84×104 B.3.84×105 C.3.84×106 D.38.4×105
4.如图,一把直尺、两个含30°的三角尺拼接在一起,则∠ACE的度数为( )
A.120° B.90° C.60° D.30°
5.下列计算正确的是( )
A.a2 a5=a10 B.a8÷a2=a4 C.﹣2a+5a=7a D.(a2)5=a10
6.长江是中华民族的母亲河,长江流域孕育出藏羌文化、巴蜀文化、荆楚文化、吴越文化等区域文化.若从上述四种区域文化中随机选一种文化开展专题学习,则选中“巴蜀文化”的概率是( )
A. B. C. D.
7.完全相同的4个正方形面积之和是100,则正方形的边长是( )
A.2 B.5 C.10 D.20
8.若点(0,y1),(1,y2),(2,y3)都在二次函数y=x2的图象上,则( )
A.y3>y2>y1 B.y2>y1>y3 C.y1>y3>y2 D.y3>y1>y2
9.方程的解是( )
A.x=﹣3 B.x=﹣9 C.x=3 D.x=9
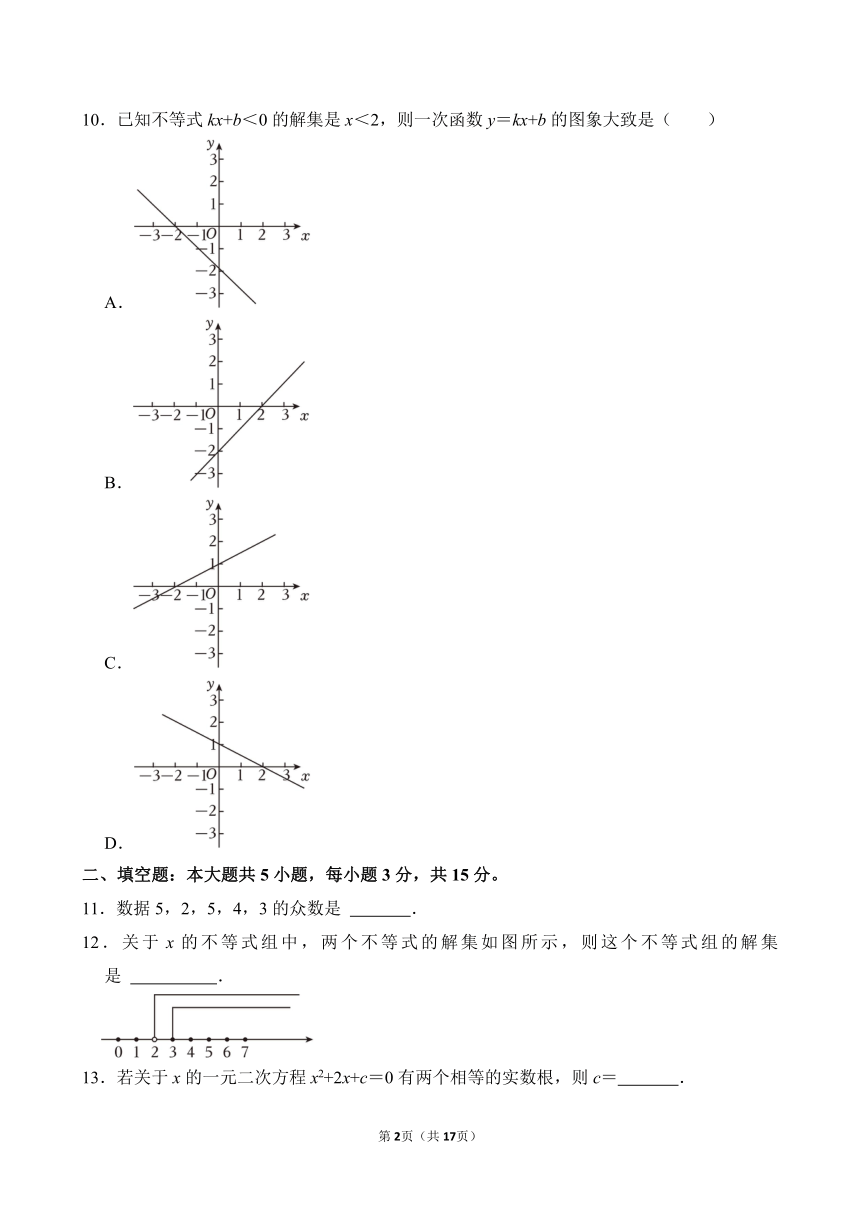
10.已知不等式kx+b<0的解集是x<2,则一次函数y=kx+b的图象大致是( )
A.
B.
C.
D.
二、填空题:本大题共5小题,每小题3分,共15分。
11.数据5,2,5,4,3的众数是 .
12.关于x的不等式组中,两个不等式的解集如图所示,则这个不等式组的解集是 .
13.若关于x的一元二次方程x2+2x+c=0有两个相等的实数根,则c= .
14.计算: .
15.如图,菱形ABCD的面积为24,点E是AB的中点,点F是BC上的动点.若△BEF的面积为4,则图中阴影部分的面积为 .
三、解答题(一):本大题共3小题,每小题7分,共21分.
16.计算:20×||3﹣1.
17.如图,在△ABC中,∠C=90°.
(1)实践与操作:用尺规作图法作∠A的平分线AD交BC于点D;(保留作图痕迹,不要求写作法)
(2)应用与证明:在(1)的条件下,以点D为圆心,DC长为半径作⊙D.求证:AB与⊙D相切.
18.中国新能源汽车为全球应对气候变化和绿色低碳转型作出了巨大贡献.为满足新能源汽车的充电需求,某小区增设了充电站,如图是矩形PQMN充电站的平面示意图,矩形ABCD是其中一个停车位.经测量,∠ABQ=60°,AB=5.4m,CE=1.6m,GH⊥CD,GH是另一个车位的宽,所有车位的长宽相同,按图示并列划定.
根据以上信息回答下列问题:(结果精确到0.1m,参考数据1.73)
(1)求PQ的长;
(2)该充电站有20个停车位,求PN的长.
四、解答题(二):本大题共3小题,每小题9分,共27分。
19.端午假期,王先生计划与家人一同前往景区游玩.为了选择一个最合适的景区,王先生对A、B、C三个景区进行了调查与评估.他依据特色美食、自然风光、乡村民宿及科普基地四个方面,为每个景区评分(10分制).三个景区的得分如表所示:
景区 特色美食 自然风光 乡村民宿 科普基地
A 6 8 7 9
B 7 7 8 7
C 8 8 6 6
(1)若四项所占百分比如图所示,通过计算回答:王先生会选择哪个景区去游玩?
(2)如果王先生认为四项同等重要,通过计算回答:王先生将会选择哪个景区去游玩?
(3)如果你是王先生,请按你认为的各项“重要程度”设计四项得分的百分比,选择最合适的景区,并说明理由.
20.广东省全力实施“百县千镇万村高质量发展工程”,2023年农产品进出口总额居全国首位,其中荔枝鲜果远销欧美.某果商以每吨2万元的价格收购早熟荔枝,销往国外,若按每吨5万元出售,平均每天可售出100吨.市场调查反映:如果每吨降价1万元,每天销售量相应增加50吨.该果商如何定价才能使每天的“利润”或“销售收入”最大?并求出其最大值.(题中“元”为人民币)
21.综合与实践
【主题】滤纸与漏斗
【素材】如图1所示:
①一张直径为10cm的圆形滤纸;
②一只漏斗口直径与母线均为7cm的圆锥形过滤漏斗.
【实践操作】
步骤1:取一张滤纸;
步骤2:按如图2所示步骤折叠好滤纸;
步骤3:将其中一层撑开,围成圆锥形;
步骤4:将围成圆锥形的滤纸放入如图1所示漏斗中.
【实践探索】
(1)滤纸是否能紧贴此漏斗内壁(忽略漏斗管口处)?用你所学的数学知识说明.
(2)当滤纸紧贴漏斗内壁时,求滤纸围成圆锥形的体积.(结果保留π)
五、解答题(三):本大题共2小题,第22题13分,第23题14分,共27分。
22.(13分)【知识技能】
(1)如图1,在△ABC中,DE是△ABC的中位线.连接CD,将△ADC绕点D按逆时针方向旋转,得到△A′DC′.当点E的对应点E′与点A重合时,求证:AB=BC.
【数学理解】
(2)如图2,在△ABC中(AB<BC),DE是△ABC的中位线.连接CD,将△ADC绕点D按逆时针方向旋转,得到△A′DC′,连接A′B,C′C,作△A′BD的中线DF.求证:2DF CD=BD CC′.
【拓展探索】
(3)如图3,在△ABC中,tanB,点D在AB上,AD.过点D作DE⊥BC,垂足为E,BE=3,CE.在四边形ADEC内是否存在点G,使得∠AGD+∠CGE=180°?若存在,请给出证明;若不存在,请说明理由.
23.(14分)【问题背景】
如图1,在平面直角坐标系中,点B,D是直线y=ax(a>0)上第一象限内的两个动点(OD>OB),以线段BD为对角线作矩形ABCD,AD∥x轴.反比例函数y的图象经过点A.
【构建联系】
(1)求证:函数y的图象必经过点C.
(2)如图2,把矩形ABCD沿BD折叠,点C的对应点为E.当点E落在y轴上,且点B的坐标为(1,2)时,求k的值.
【深入探究】
(3)如图3,把矩形ABCD沿BD折叠,点C的对应点为E.当点E,A重合时,连接AC交BD于点P.以点O为圆心,AC长为半径作⊙O.若OP=3,当⊙O与△ABC的边有交点时,求k的取值范围.
2024年广东省中考数学试卷
答案解析
一、选择题:本大题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.A
2.C
3.B
4.C
5.D
6.A
7.B
8.A
解析:∵二次函数y=x2,
∴该二次函数的抛物线开口向上,且对称轴为y轴.
∴当x≥0时,y随x的增大而增大,
∵0<1<2,
∴y1<y2<y3,
故选:A.
9.D
解析:,
2x=3(x﹣3),
解得:x=9,
检验:当x=9时,x(x﹣3)≠0,
∴x=9是原方程的根,
故选:D.
10.B
解析:A.不等式kx+b<0的解集是x>﹣2,故本选项不符合题意;
B.不等式kx+b<0的解集是x<2,故本选项符合题意;
C.不等式kx+b<0的解集是x<﹣2,故本选项不符合题意;
D.不等式kx+b<0的解集是x>2,故本选项不符合题意;
故选:B.
二、填空题:本大题共5小题,每小题3分,共15分。
11.5
12.x≥3
13.1
14.1
15.10
解析:连接BD,
∵E是AB的中点,
∴S△AEDS△ABDS菱形ABCD=6,
连接EC,
同理可得S△BEC=S△AED=6,
∵S△BEF=4,
∴S△BEFS△BEC,
∴FCBC,
∴S△DFCS△BCDS菱形ABCD=4,
∴S阴影=S菱形ABCD﹣S△AED﹣S△BEF﹣S△DFC=24﹣6﹣4﹣4=10.
故答案为:10.
三、解答题(一):本大题共3小题,每小题7分,共21分.
16.解:原式=12
2
=2.
17.(1)解:如图,AD即为所求.
(2)证明:过点D作DE⊥AB于点E,
∵AD平分∠BAC,∠C=90°,
∴DE=CD,
∴DE为⊙D的半径,
∴AB与⊙D相切.
18.解:(1)∵四边形PQMN是矩形,
∴∠Q=∠P=90°,
在Rt△ABQ中,∠ABQ=60°,AB=5.4m,
∴AQ=AB sin,∠QAB=30°,
∵四边形ABCD是矩形,
∴AD=BC,∠BAD=∠BCD=∠ABC=∠BCE=90°,
∴∠CBE=30°,
∴,
∴,
∵∠PAD=180°﹣30°﹣90°=60°,
∴,
∴;
(2)在Rt△BCE中,,
在Rt△ABQ中,BQ=AB cos∠ABQ=2.7m,
∵该充电站有20个停车位,
∴QM=QB+20BE=66.7m,
∵四边形ABCD是矩形,
∴PN=QM=66.7m.
四、解答题(二):本大题共3小题,每小题9分,共27分。
19.解:(1)景区A得分为:7.15,
景区B得分为:7.4,
景区C得分为:6.9,
∵7.4>7.15>6.9,
∴王先生会选择B景区去游玩;
(2)景区A得分为:7.5,
景区B得分为:7.25,
景区C得分为:7,
∵7.5>7.25>7,
∴王先生会选择A景区去游玩;
(3)将特色美食、自然风光、乡村民宿和科普基地四项得分的百分比定为20%,30%,30%,20%,
景区A得分为:7.5,
景区B得分为:7.3,
景区C得分为:7,
∵7.5>7.3>7,
∴选择A景区去游玩.
20.解:设该果商定价x万元时每天的“利润”为w万元,
w=(x﹣2)[100+50(5﹣x)]
=﹣50(x﹣4.5)2+312.5,
∵﹣50<0,
∴w随x的增大而减小,
∴当x=4.5时,w有最大值,最大值为312.5万元,
答:该果商定价为4.5万元时才能使每天的“利润”或“销售收入”最大,其最大值为312.5万元.
21.解:(1)滤纸能紧贴此漏斗内壁,理由如下,
方法一:如图作出示意图,由题意知,AB=AC=BC=7cm,
折叠后CD=CE10=5cm,
∵底面周长10π=5πcm,
∴DE π=5πcm,
∴DE=5cm,
∴,
∴△CDE∽△CAB,
∴滤纸能紧贴此漏斗内壁.
方法二:由2πr得,
图3中,n1=90°×2=180°,
图4中,,
∴n2=180°,
∵n1=n2,
∴滤纸能紧贴此漏斗内壁.
(2)由(1)知CD=DE=CE=5cm,
∴∠CDE=60°,
过C作CF⊥DE于点F,则DFDEcm,
在Rt△CDF中,CF2cm,
∴V=π ()2πcm3.
即圆锥形的体积是πcm3.
五、解答题(三):本大题共2小题,第22题13分,第23题14分,共27分。
22.(13分)(1)证明:∵△ADC绕点D按逆时针方向旋转,得到△A′DC',且E'与A重合,
∴AD=AE,
∴∠DAE=∠DEA,
∵DE是△ABC的中位线,
∴DE∥BC,
∴∠DEA=∠BCA,
∴∠DAE=∠BCA,
∴AB=AC.
(2)证明:连接AA',
∵旋转,
∴∠ADA′=∠CDC′,AD=A'D,CD=C'D,
∴,
∴△ADA′∽△CDC′,
∴,
∵DE是△ABC的中位线,DF是△A'BD的中线,
∴AD=BD,BF=A'F,
∴DF是△AA'B的中位线,
∴AA'=2DF,
∴,
∴2DF CD=BD CC'
(3)解:存在,理由如下,
取AD中点M,CE中点N,连接MN,
∵AD是⊙M直径,CE是⊙N直径,
∴∠AGD=90°,∠CGE=90°,
∴∠AGD+∠CGE=180°,
∵tanB,BE=3,
∴BD=5,
∵CE,
∴ENCE,
∴BN=BE+EN,
∵DE⊥CE,
∴DE是⊙N的切线,即DE在⊙N外,
作NF⊥AB,
∵∠B=∠B,∠BED=∠BFN=90°,
∴△BDE∽△BNF,
∴,
∴NF,即NF>rn,
∴AB在⊙N外,
∴G点在四边形ADEC内部.
故四边形ADEC内存在点G,使得∠AGD+∠CGE=180°.
23.(14分)解:(1)设B(m,ma),则,
∵AD∥x轴,
∴D点的纵坐标为,
将代入y=ax中,得:,
∴,
∴,
∴,
将代入中得出,y=am,
∴函数的图象必经过点C;
(2)∵点B(1,2)在直线y=ax上,
∴a=2,
∴y=2x,
∴A点的横坐标为1,C点的纵坐标为2,
∵函数的图象经过点A,C,
∴,A(1,k),
∴,
∴DC=k﹣2,
∵把矩形ABCD沿BD折叠,点C的对应点为E,
∴,∠BED=∠BCD=90°,
∴,
如图,过点D作DH⊥y轴,过点B作BF⊥y轴,
∵AD∥x轴,
∴H,A,D三点共线,
∴∠HED+∠BEF=90°,∠BEF+∠EBF=90°,
∴∠HED=∠EBF,
∵∠DHE=∠EFB=90°,
∴△DHE∽△EFB,
∴,
∵BF=1,,
∴HE=2,,
∴,
由图知,HF=DC,
∴,
∴;
(3)∵把矩形ABCD沿BD折叠,点C的对应点为E,当点E,A重合,
∴AC⊥BD,
∵四边形ABCD为矩形,
∴四边形ABCD为正方形,∠ABP=∠DBC=45°,
∴,,BP⊥AC,
∵BC∥x轴,
∴直线y=a为一,三象限的夹角平分线,
∴y=x,
当⊙O过点B时,如图所示,过点D作DH∥x轴交y轴于点H,
∵AD∥x轴,
∴H,A,D三点共线,
∵以点O为圆心,AC长为半径作⊙O,,
∴,
∴,
∴,,,
∵AB∥y轴,
∴△DHO∽△DAB,
∴,
∴,
∴HO=HD=4,
∴HA=HD﹣DA=4﹣2=2,
∴A(2,4),
∴k=2×4=8,
当⊙O过点A时,根据A,C关于直线OD对称知,⊙O必过点C,如图所示,连AO,CO,过点D作DH∥x轴交y轴于点H,
∵AO=OC=AC,
∴△AOC为等边三角形,
∵OP⊥AC,
∴,
∴,,
∴,,
∵AB∥y轴,
∴△DHO∽△DAB,
∴,
∴,
∴,
∴,
∴,
∴,
∴当⊙O与△ABC的边有交点时,k的取值范围为6≤k≤8.
第1页(共1页)
一、选择题:本大题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.计算﹣5+3的结果是( )
A.﹣2 B.﹣8 C.2 D.8
2.下列几何图形中,既是中心对称图形也是轴对称图形的是( )
A. B. C. D.
3.2024年6月6日,嫦娥六号在距离地球约384000千米外上演“太空牵手”,完成月球轨道的交会对接.数据384000用科学记数法表示为( )
A.3.84×104 B.3.84×105 C.3.84×106 D.38.4×105
4.如图,一把直尺、两个含30°的三角尺拼接在一起,则∠ACE的度数为( )
A.120° B.90° C.60° D.30°
5.下列计算正确的是( )
A.a2 a5=a10 B.a8÷a2=a4 C.﹣2a+5a=7a D.(a2)5=a10
6.长江是中华民族的母亲河,长江流域孕育出藏羌文化、巴蜀文化、荆楚文化、吴越文化等区域文化.若从上述四种区域文化中随机选一种文化开展专题学习,则选中“巴蜀文化”的概率是( )
A. B. C. D.
7.完全相同的4个正方形面积之和是100,则正方形的边长是( )
A.2 B.5 C.10 D.20
8.若点(0,y1),(1,y2),(2,y3)都在二次函数y=x2的图象上,则( )
A.y3>y2>y1 B.y2>y1>y3 C.y1>y3>y2 D.y3>y1>y2
9.方程的解是( )
A.x=﹣3 B.x=﹣9 C.x=3 D.x=9
10.已知不等式kx+b<0的解集是x<2,则一次函数y=kx+b的图象大致是( )
A.
B.
C.
D.
二、填空题:本大题共5小题,每小题3分,共15分。
11.数据5,2,5,4,3的众数是 .
12.关于x的不等式组中,两个不等式的解集如图所示,则这个不等式组的解集是 .
13.若关于x的一元二次方程x2+2x+c=0有两个相等的实数根,则c= .
14.计算: .
15.如图,菱形ABCD的面积为24,点E是AB的中点,点F是BC上的动点.若△BEF的面积为4,则图中阴影部分的面积为 .
三、解答题(一):本大题共3小题,每小题7分,共21分.
16.计算:20×||3﹣1.
17.如图,在△ABC中,∠C=90°.
(1)实践与操作:用尺规作图法作∠A的平分线AD交BC于点D;(保留作图痕迹,不要求写作法)
(2)应用与证明:在(1)的条件下,以点D为圆心,DC长为半径作⊙D.求证:AB与⊙D相切.
18.中国新能源汽车为全球应对气候变化和绿色低碳转型作出了巨大贡献.为满足新能源汽车的充电需求,某小区增设了充电站,如图是矩形PQMN充电站的平面示意图,矩形ABCD是其中一个停车位.经测量,∠ABQ=60°,AB=5.4m,CE=1.6m,GH⊥CD,GH是另一个车位的宽,所有车位的长宽相同,按图示并列划定.
根据以上信息回答下列问题:(结果精确到0.1m,参考数据1.73)
(1)求PQ的长;
(2)该充电站有20个停车位,求PN的长.
四、解答题(二):本大题共3小题,每小题9分,共27分。
19.端午假期,王先生计划与家人一同前往景区游玩.为了选择一个最合适的景区,王先生对A、B、C三个景区进行了调查与评估.他依据特色美食、自然风光、乡村民宿及科普基地四个方面,为每个景区评分(10分制).三个景区的得分如表所示:
景区 特色美食 自然风光 乡村民宿 科普基地
A 6 8 7 9
B 7 7 8 7
C 8 8 6 6
(1)若四项所占百分比如图所示,通过计算回答:王先生会选择哪个景区去游玩?
(2)如果王先生认为四项同等重要,通过计算回答:王先生将会选择哪个景区去游玩?
(3)如果你是王先生,请按你认为的各项“重要程度”设计四项得分的百分比,选择最合适的景区,并说明理由.
20.广东省全力实施“百县千镇万村高质量发展工程”,2023年农产品进出口总额居全国首位,其中荔枝鲜果远销欧美.某果商以每吨2万元的价格收购早熟荔枝,销往国外,若按每吨5万元出售,平均每天可售出100吨.市场调查反映:如果每吨降价1万元,每天销售量相应增加50吨.该果商如何定价才能使每天的“利润”或“销售收入”最大?并求出其最大值.(题中“元”为人民币)
21.综合与实践
【主题】滤纸与漏斗
【素材】如图1所示:
①一张直径为10cm的圆形滤纸;
②一只漏斗口直径与母线均为7cm的圆锥形过滤漏斗.
【实践操作】
步骤1:取一张滤纸;
步骤2:按如图2所示步骤折叠好滤纸;
步骤3:将其中一层撑开,围成圆锥形;
步骤4:将围成圆锥形的滤纸放入如图1所示漏斗中.
【实践探索】
(1)滤纸是否能紧贴此漏斗内壁(忽略漏斗管口处)?用你所学的数学知识说明.
(2)当滤纸紧贴漏斗内壁时,求滤纸围成圆锥形的体积.(结果保留π)
五、解答题(三):本大题共2小题,第22题13分,第23题14分,共27分。
22.(13分)【知识技能】
(1)如图1,在△ABC中,DE是△ABC的中位线.连接CD,将△ADC绕点D按逆时针方向旋转,得到△A′DC′.当点E的对应点E′与点A重合时,求证:AB=BC.
【数学理解】
(2)如图2,在△ABC中(AB<BC),DE是△ABC的中位线.连接CD,将△ADC绕点D按逆时针方向旋转,得到△A′DC′,连接A′B,C′C,作△A′BD的中线DF.求证:2DF CD=BD CC′.
【拓展探索】
(3)如图3,在△ABC中,tanB,点D在AB上,AD.过点D作DE⊥BC,垂足为E,BE=3,CE.在四边形ADEC内是否存在点G,使得∠AGD+∠CGE=180°?若存在,请给出证明;若不存在,请说明理由.
23.(14分)【问题背景】
如图1,在平面直角坐标系中,点B,D是直线y=ax(a>0)上第一象限内的两个动点(OD>OB),以线段BD为对角线作矩形ABCD,AD∥x轴.反比例函数y的图象经过点A.
【构建联系】
(1)求证:函数y的图象必经过点C.
(2)如图2,把矩形ABCD沿BD折叠,点C的对应点为E.当点E落在y轴上,且点B的坐标为(1,2)时,求k的值.
【深入探究】
(3)如图3,把矩形ABCD沿BD折叠,点C的对应点为E.当点E,A重合时,连接AC交BD于点P.以点O为圆心,AC长为半径作⊙O.若OP=3,当⊙O与△ABC的边有交点时,求k的取值范围.
2024年广东省中考数学试卷
答案解析
一、选择题:本大题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.A
2.C
3.B
4.C
5.D
6.A
7.B
8.A
解析:∵二次函数y=x2,
∴该二次函数的抛物线开口向上,且对称轴为y轴.
∴当x≥0时,y随x的增大而增大,
∵0<1<2,
∴y1<y2<y3,
故选:A.
9.D
解析:,
2x=3(x﹣3),
解得:x=9,
检验:当x=9时,x(x﹣3)≠0,
∴x=9是原方程的根,
故选:D.
10.B
解析:A.不等式kx+b<0的解集是x>﹣2,故本选项不符合题意;
B.不等式kx+b<0的解集是x<2,故本选项符合题意;
C.不等式kx+b<0的解集是x<﹣2,故本选项不符合题意;
D.不等式kx+b<0的解集是x>2,故本选项不符合题意;
故选:B.
二、填空题:本大题共5小题,每小题3分,共15分。
11.5
12.x≥3
13.1
14.1
15.10
解析:连接BD,
∵E是AB的中点,
∴S△AEDS△ABDS菱形ABCD=6,
连接EC,
同理可得S△BEC=S△AED=6,
∵S△BEF=4,
∴S△BEFS△BEC,
∴FCBC,
∴S△DFCS△BCDS菱形ABCD=4,
∴S阴影=S菱形ABCD﹣S△AED﹣S△BEF﹣S△DFC=24﹣6﹣4﹣4=10.
故答案为:10.
三、解答题(一):本大题共3小题,每小题7分,共21分.
16.解:原式=12
2
=2.
17.(1)解:如图,AD即为所求.
(2)证明:过点D作DE⊥AB于点E,
∵AD平分∠BAC,∠C=90°,
∴DE=CD,
∴DE为⊙D的半径,
∴AB与⊙D相切.
18.解:(1)∵四边形PQMN是矩形,
∴∠Q=∠P=90°,
在Rt△ABQ中,∠ABQ=60°,AB=5.4m,
∴AQ=AB sin,∠QAB=30°,
∵四边形ABCD是矩形,
∴AD=BC,∠BAD=∠BCD=∠ABC=∠BCE=90°,
∴∠CBE=30°,
∴,
∴,
∵∠PAD=180°﹣30°﹣90°=60°,
∴,
∴;
(2)在Rt△BCE中,,
在Rt△ABQ中,BQ=AB cos∠ABQ=2.7m,
∵该充电站有20个停车位,
∴QM=QB+20BE=66.7m,
∵四边形ABCD是矩形,
∴PN=QM=66.7m.
四、解答题(二):本大题共3小题,每小题9分,共27分。
19.解:(1)景区A得分为:7.15,
景区B得分为:7.4,
景区C得分为:6.9,
∵7.4>7.15>6.9,
∴王先生会选择B景区去游玩;
(2)景区A得分为:7.5,
景区B得分为:7.25,
景区C得分为:7,
∵7.5>7.25>7,
∴王先生会选择A景区去游玩;
(3)将特色美食、自然风光、乡村民宿和科普基地四项得分的百分比定为20%,30%,30%,20%,
景区A得分为:7.5,
景区B得分为:7.3,
景区C得分为:7,
∵7.5>7.3>7,
∴选择A景区去游玩.
20.解:设该果商定价x万元时每天的“利润”为w万元,
w=(x﹣2)[100+50(5﹣x)]
=﹣50(x﹣4.5)2+312.5,
∵﹣50<0,
∴w随x的增大而减小,
∴当x=4.5时,w有最大值,最大值为312.5万元,
答:该果商定价为4.5万元时才能使每天的“利润”或“销售收入”最大,其最大值为312.5万元.
21.解:(1)滤纸能紧贴此漏斗内壁,理由如下,
方法一:如图作出示意图,由题意知,AB=AC=BC=7cm,
折叠后CD=CE10=5cm,
∵底面周长10π=5πcm,
∴DE π=5πcm,
∴DE=5cm,
∴,
∴△CDE∽△CAB,
∴滤纸能紧贴此漏斗内壁.
方法二:由2πr得,
图3中,n1=90°×2=180°,
图4中,,
∴n2=180°,
∵n1=n2,
∴滤纸能紧贴此漏斗内壁.
(2)由(1)知CD=DE=CE=5cm,
∴∠CDE=60°,
过C作CF⊥DE于点F,则DFDEcm,
在Rt△CDF中,CF2cm,
∴V=π ()2πcm3.
即圆锥形的体积是πcm3.
五、解答题(三):本大题共2小题,第22题13分,第23题14分,共27分。
22.(13分)(1)证明:∵△ADC绕点D按逆时针方向旋转,得到△A′DC',且E'与A重合,
∴AD=AE,
∴∠DAE=∠DEA,
∵DE是△ABC的中位线,
∴DE∥BC,
∴∠DEA=∠BCA,
∴∠DAE=∠BCA,
∴AB=AC.
(2)证明:连接AA',
∵旋转,
∴∠ADA′=∠CDC′,AD=A'D,CD=C'D,
∴,
∴△ADA′∽△CDC′,
∴,
∵DE是△ABC的中位线,DF是△A'BD的中线,
∴AD=BD,BF=A'F,
∴DF是△AA'B的中位线,
∴AA'=2DF,
∴,
∴2DF CD=BD CC'
(3)解:存在,理由如下,
取AD中点M,CE中点N,连接MN,
∵AD是⊙M直径,CE是⊙N直径,
∴∠AGD=90°,∠CGE=90°,
∴∠AGD+∠CGE=180°,
∵tanB,BE=3,
∴BD=5,
∵CE,
∴ENCE,
∴BN=BE+EN,
∵DE⊥CE,
∴DE是⊙N的切线,即DE在⊙N外,
作NF⊥AB,
∵∠B=∠B,∠BED=∠BFN=90°,
∴△BDE∽△BNF,
∴,
∴NF,即NF>rn,
∴AB在⊙N外,
∴G点在四边形ADEC内部.
故四边形ADEC内存在点G,使得∠AGD+∠CGE=180°.
23.(14分)解:(1)设B(m,ma),则,
∵AD∥x轴,
∴D点的纵坐标为,
将代入y=ax中,得:,
∴,
∴,
∴,
将代入中得出,y=am,
∴函数的图象必经过点C;
(2)∵点B(1,2)在直线y=ax上,
∴a=2,
∴y=2x,
∴A点的横坐标为1,C点的纵坐标为2,
∵函数的图象经过点A,C,
∴,A(1,k),
∴,
∴DC=k﹣2,
∵把矩形ABCD沿BD折叠,点C的对应点为E,
∴,∠BED=∠BCD=90°,
∴,
如图,过点D作DH⊥y轴,过点B作BF⊥y轴,
∵AD∥x轴,
∴H,A,D三点共线,
∴∠HED+∠BEF=90°,∠BEF+∠EBF=90°,
∴∠HED=∠EBF,
∵∠DHE=∠EFB=90°,
∴△DHE∽△EFB,
∴,
∵BF=1,,
∴HE=2,,
∴,
由图知,HF=DC,
∴,
∴;
(3)∵把矩形ABCD沿BD折叠,点C的对应点为E,当点E,A重合,
∴AC⊥BD,
∵四边形ABCD为矩形,
∴四边形ABCD为正方形,∠ABP=∠DBC=45°,
∴,,BP⊥AC,
∵BC∥x轴,
∴直线y=a为一,三象限的夹角平分线,
∴y=x,
当⊙O过点B时,如图所示,过点D作DH∥x轴交y轴于点H,
∵AD∥x轴,
∴H,A,D三点共线,
∵以点O为圆心,AC长为半径作⊙O,,
∴,
∴,
∴,,,
∵AB∥y轴,
∴△DHO∽△DAB,
∴,
∴,
∴HO=HD=4,
∴HA=HD﹣DA=4﹣2=2,
∴A(2,4),
∴k=2×4=8,
当⊙O过点A时,根据A,C关于直线OD对称知,⊙O必过点C,如图所示,连AO,CO,过点D作DH∥x轴交y轴于点H,
∵AO=OC=AC,
∴△AOC为等边三角形,
∵OP⊥AC,
∴,
∴,,
∴,,
∵AB∥y轴,
∴△DHO∽△DAB,
∴,
∴,
∴,
∴,
∴,
∴,
∴当⊙O与△ABC的边有交点时,k的取值范围为6≤k≤8.
第1页(共1页)
同课章节目录
