2023-2024学年重庆市九龙坡区渝西中学高二(下)月考数学试卷(6月份)(含答案)
文档属性
| 名称 | 2023-2024学年重庆市九龙坡区渝西中学高二(下)月考数学试卷(6月份)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 96.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-03 15:39:11 | ||
图片预览



文档简介
2023-2024学年重庆市九龙坡区渝西中学高二(下)月考数学试卷(6月份)
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.命题“,”的否定是( )
A. , B. ,
C. , D. ,
2.集合,,若,则实数( )
A. B. C. D.
3.已知,,则的取值范围是( )
A. B. C. D.
4.已知变量,呈线性相关关系,回归方程为,且变量,的样本数据如下表所示
据此计算出在时,预测值为,则的值为( )
A. B. C. D.
5.已知实数,则下列不等式中一定正确的有( )
A. B.
C. D.
6.已知偶函数在上单调递减,则的大小关系为( )
A. B. C. D.
7.把二项式的所有展开项重新排列,记有理项都相邻的概率为,有理项两两不相邻的概率为,则( )
A. B. C. D.
8.对于正数,,有,则的取值范围是( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.随机变量,分别服从正态分布和二项分布,即,,则( )
A. B. C. D.
10.已知:函数的定义域为,则的必要条件可以是( )
A. 或 B. C. D.
11.已知,若对,使成立,则下列说法正确的是( )
A. 函数的最小值为
B. 当时,的解集为
C. 实数的取值范围是
D. 实数的取值范围是
三、填空题:本题共3小题,每小题5分,共15分。
12.函数的定义域是______.
13.年伊始,随着“广西沙糖桔”“马铃薯公主”等热梗的不断爆出,哈尔滨火爆出圈,成为旅游城市中的“顶流”某班级五位同学也准备共赴一场冰雪之约,制定了“南方小土豆,勇闯哈尔滨”的出游计划,这五位同学准备在行程第一天在圣索菲亚教堂,冰雪大世界,中央大街三个景点中选择一个去游玩,已知每个景点至少有一位同学会选,五位同学都会进行选择并且只能选择其中一个景点,若学生甲和学生乙准备选同一个景点,则不同的选法种数是______.
14.设是定义在上的单调增函数,且满足,若对于任意非零实数都有,则 ______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知等差数列的前项和为,且满足,.
求数列的通项公式;
若数列满足,求数列的前项和.
16.本小题分
新能源渗透率是指在一定时期内,新能源汽车销量占汽车总销量的比重在年,新能源汽车的渗透率达到了,提前三年超过了“十四五”预定的的目标年,随着技术进步,新能源车的渗透率还在继续扩大将年月视为第一个月,得到年月,我国新能源汽车渗透率如下表:
月份代码
渗透率
假设自年月起的第个月的新能源渗透率为,试求关于的回归直线方程,并由此预测年月的新能源渗透率;
为了鼓励大家购买新能源汽车,国家在年继续执行新能源车购置税优惠政策:在年月日前购买的新能源车无需支付购置税,而燃油车需按照车价支付购置税年月小张为自己的客户代付购置税,当月他的客户购买了辆车价格均为万元,假设以中预测的新能源渗透率作为当月客户购买新能源车的概率,设小张总共需要代付的购置税为万元,求的分布列和期望.
附:一组数据,,的线性回归直线方程的系数公式为:,.
17.本小题分
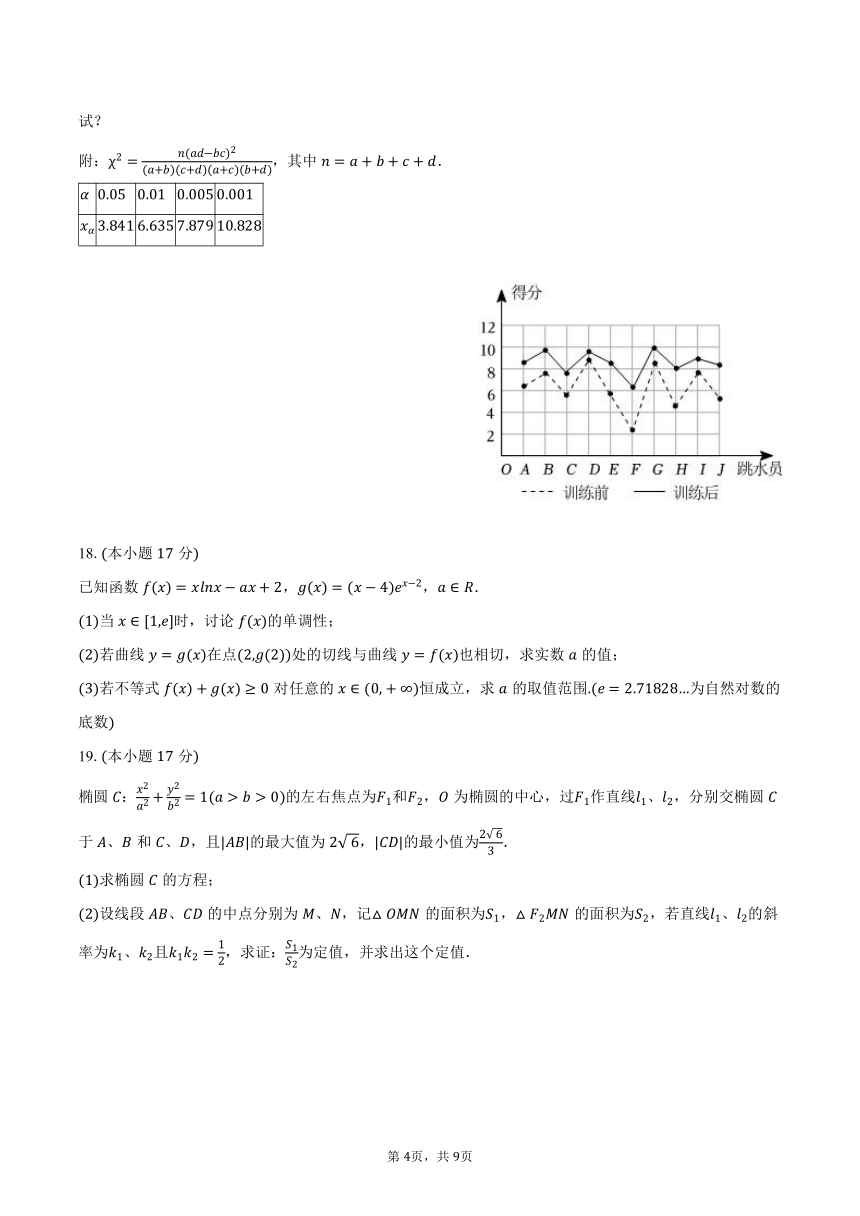
年月日,第三十一届世界大学生夏季运动会在成都隆重开幕为庆祝大运会的到来,有,,,,共位跳水爱好者自发组建了跳水训练营,并邀请教练甲帮助训练教练训练前对位跳水员测试打分,得分情况如图中虚线所示;集训后再进行测试,位跳水员得分情况如图中实线所示,规定满分为分,记得分在分以上的为“优秀”.
优秀人数 非优秀人数 合计
训练前
训练后
合计
将上面的列联表补充完整,并根据小概率值的独立性检验,判断跳水员的优秀情况与训练是否有关?并说明原因;
从这人中任选人,在这人中恰有人训练后为“优秀”的条件下,求这人中恰有人是训练前也为“优秀”的概率;
跳水员将对“米、米和米”这三种高度进行集训,且在训练中进行了多轮测试规定:在每轮测试中,都会有这种高度,且至少有个高度的跳水测试达到“优秀”,则该轮测试才记为“优秀”每轮测试中,跳水员在每个高度中达到“优秀”的概率均为,每个高度互不影响且每轮测试互不影响如果跳水员在集训测试中要想获得“优秀”的次数平均值达到次,那么理论上至少要进行多少轮测试?
附:,其中.
18.本小题分
已知函数,,.
当时,讨论的单调性;
若曲线在点处的切线与曲线也相切,求实数的值;
若不等式对任意的恒成立,求的取值范围为自然对数的底数
19.本小题分
椭圆:的左右焦点为和,为椭圆的中心,过作直线、,分别交椭圆于、和、,且的最大值为,的最小值为.
求椭圆的方程;
设线段、的中点分别为、,记的面积为,的面积为,若直线、的斜率为、且,求证:为定值,并求出这个定值.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:设等差数列的公差为,则,
解得,故;
由可得,
故
.
16.解:计算得,,
,,
,
则回归直线方程为,代入得,
所以预测年月新能源渗透率为;
由题意,每个客户购买新能源车的概率为,燃油车概率为,
所有可能取值为,,,,
则,,
,,
所以的分布列为:
所以万元.
17.解:列联表如下:
优秀人数 非优秀人数 合计
训练前
训练后
合计
零假设:假设跳水员的优秀情况与训练无关
可得,
则根据小概率值的独立性检验,零假设不成立,
即跳水员的优秀情况与训练有关,此推断犯错误的概率不超过.
易知训练前后均不优秀的有,共人,训练前后均优秀的有,共人,训练前不优秀而训练后优秀的有人,
记“所选人中恰有人训练后为优秀”为事件,
记“所选人中恰有人训练前为优秀”为事件,
可得,,
所以;
设跳水员每轮测试为优秀的概率为,
可得,
设测试次数为,
则优秀的次数,
所以,
解得,
故至少需进行轮测试.
18.解:,,
,
当时,,在上单调递增;
当时,,在上单调递减;
当时,令,则,
当时,,单调递减;
当时,,单调递增;
综上:当时,在上单调递增;
当时,在单调递减,在单调递增;
当时,在上单调递减;
函数,,
,,,,
故曲线在点处的切线方程为,
即.
设切线与曲线切于点,
则,
解得,.
法一:函数,定义域为,
故,
等价于,
记,
令,,
解得,,解得,
故在上单调递减,在上单调递增,
当时,.
解得,,解得,
故F在单调递减,在单调递增,
有,
因此的取值范围为.
法二:取,由,得.
下证:当时,恒成立.
记,
由,函数在单调递减,
,
记,,
,
记,,
,解得,解得,
故在单调递减,在单调递增,
故,
故,在上单调递增,即在上单调递增,
又,
在上恒成立,在恒成立,
在单调递减,在单调递增,
,得证.
综上知,的取值范围为.
19.解:因为过椭圆的左焦点作直线、,分别交椭圆于、和、,
易知当为轴时,取得最大值,
此时,
解得,
当轴时,取得最小值,
此时直线的方程为,
当,解得,
所以,
联立,解得,,
则椭圆的方程为;
证明:由知,,
不妨设直线的方程为,直线的方程为,其中,,
所以,
联立,
消去并整理得,
此时,
不妨设,,,
由韦达定理得,,
此时,,
所以,
同理得,
不妨设直线的斜率为,
此时,
则直线的方程为,
即,
因为,
所以,
则直线恒过定点,
而点与点到直线的距离之比,
故
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.命题“,”的否定是( )
A. , B. ,
C. , D. ,
2.集合,,若,则实数( )
A. B. C. D.
3.已知,,则的取值范围是( )
A. B. C. D.
4.已知变量,呈线性相关关系,回归方程为,且变量,的样本数据如下表所示
据此计算出在时,预测值为,则的值为( )
A. B. C. D.
5.已知实数,则下列不等式中一定正确的有( )
A. B.
C. D.
6.已知偶函数在上单调递减,则的大小关系为( )
A. B. C. D.
7.把二项式的所有展开项重新排列,记有理项都相邻的概率为,有理项两两不相邻的概率为,则( )
A. B. C. D.
8.对于正数,,有,则的取值范围是( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.随机变量,分别服从正态分布和二项分布,即,,则( )
A. B. C. D.
10.已知:函数的定义域为,则的必要条件可以是( )
A. 或 B. C. D.
11.已知,若对,使成立,则下列说法正确的是( )
A. 函数的最小值为
B. 当时,的解集为
C. 实数的取值范围是
D. 实数的取值范围是
三、填空题:本题共3小题,每小题5分,共15分。
12.函数的定义域是______.
13.年伊始,随着“广西沙糖桔”“马铃薯公主”等热梗的不断爆出,哈尔滨火爆出圈,成为旅游城市中的“顶流”某班级五位同学也准备共赴一场冰雪之约,制定了“南方小土豆,勇闯哈尔滨”的出游计划,这五位同学准备在行程第一天在圣索菲亚教堂,冰雪大世界,中央大街三个景点中选择一个去游玩,已知每个景点至少有一位同学会选,五位同学都会进行选择并且只能选择其中一个景点,若学生甲和学生乙准备选同一个景点,则不同的选法种数是______.
14.设是定义在上的单调增函数,且满足,若对于任意非零实数都有,则 ______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知等差数列的前项和为,且满足,.
求数列的通项公式;
若数列满足,求数列的前项和.
16.本小题分
新能源渗透率是指在一定时期内,新能源汽车销量占汽车总销量的比重在年,新能源汽车的渗透率达到了,提前三年超过了“十四五”预定的的目标年,随着技术进步,新能源车的渗透率还在继续扩大将年月视为第一个月,得到年月,我国新能源汽车渗透率如下表:
月份代码
渗透率
假设自年月起的第个月的新能源渗透率为,试求关于的回归直线方程,并由此预测年月的新能源渗透率;
为了鼓励大家购买新能源汽车,国家在年继续执行新能源车购置税优惠政策:在年月日前购买的新能源车无需支付购置税,而燃油车需按照车价支付购置税年月小张为自己的客户代付购置税,当月他的客户购买了辆车价格均为万元,假设以中预测的新能源渗透率作为当月客户购买新能源车的概率,设小张总共需要代付的购置税为万元,求的分布列和期望.
附:一组数据,,的线性回归直线方程的系数公式为:,.
17.本小题分
年月日,第三十一届世界大学生夏季运动会在成都隆重开幕为庆祝大运会的到来,有,,,,共位跳水爱好者自发组建了跳水训练营,并邀请教练甲帮助训练教练训练前对位跳水员测试打分,得分情况如图中虚线所示;集训后再进行测试,位跳水员得分情况如图中实线所示,规定满分为分,记得分在分以上的为“优秀”.
优秀人数 非优秀人数 合计
训练前
训练后
合计
将上面的列联表补充完整,并根据小概率值的独立性检验,判断跳水员的优秀情况与训练是否有关?并说明原因;
从这人中任选人,在这人中恰有人训练后为“优秀”的条件下,求这人中恰有人是训练前也为“优秀”的概率;
跳水员将对“米、米和米”这三种高度进行集训,且在训练中进行了多轮测试规定:在每轮测试中,都会有这种高度,且至少有个高度的跳水测试达到“优秀”,则该轮测试才记为“优秀”每轮测试中,跳水员在每个高度中达到“优秀”的概率均为,每个高度互不影响且每轮测试互不影响如果跳水员在集训测试中要想获得“优秀”的次数平均值达到次,那么理论上至少要进行多少轮测试?
附:,其中.
18.本小题分
已知函数,,.
当时,讨论的单调性;
若曲线在点处的切线与曲线也相切,求实数的值;
若不等式对任意的恒成立,求的取值范围为自然对数的底数
19.本小题分
椭圆:的左右焦点为和,为椭圆的中心,过作直线、,分别交椭圆于、和、,且的最大值为,的最小值为.
求椭圆的方程;
设线段、的中点分别为、,记的面积为,的面积为,若直线、的斜率为、且,求证:为定值,并求出这个定值.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:设等差数列的公差为,则,
解得,故;
由可得,
故
.
16.解:计算得,,
,,
,
则回归直线方程为,代入得,
所以预测年月新能源渗透率为;
由题意,每个客户购买新能源车的概率为,燃油车概率为,
所有可能取值为,,,,
则,,
,,
所以的分布列为:
所以万元.
17.解:列联表如下:
优秀人数 非优秀人数 合计
训练前
训练后
合计
零假设:假设跳水员的优秀情况与训练无关
可得,
则根据小概率值的独立性检验,零假设不成立,
即跳水员的优秀情况与训练有关,此推断犯错误的概率不超过.
易知训练前后均不优秀的有,共人,训练前后均优秀的有,共人,训练前不优秀而训练后优秀的有人,
记“所选人中恰有人训练后为优秀”为事件,
记“所选人中恰有人训练前为优秀”为事件,
可得,,
所以;
设跳水员每轮测试为优秀的概率为,
可得,
设测试次数为,
则优秀的次数,
所以,
解得,
故至少需进行轮测试.
18.解:,,
,
当时,,在上单调递增;
当时,,在上单调递减;
当时,令,则,
当时,,单调递减;
当时,,单调递增;
综上:当时,在上单调递增;
当时,在单调递减,在单调递增;
当时,在上单调递减;
函数,,
,,,,
故曲线在点处的切线方程为,
即.
设切线与曲线切于点,
则,
解得,.
法一:函数,定义域为,
故,
等价于,
记,
令,,
解得,,解得,
故在上单调递减,在上单调递增,
当时,.
解得,,解得,
故F在单调递减,在单调递增,
有,
因此的取值范围为.
法二:取,由,得.
下证:当时,恒成立.
记,
由,函数在单调递减,
,
记,,
,
记,,
,解得,解得,
故在单调递减,在单调递增,
故,
故,在上单调递增,即在上单调递增,
又,
在上恒成立,在恒成立,
在单调递减,在单调递增,
,得证.
综上知,的取值范围为.
19.解:因为过椭圆的左焦点作直线、,分别交椭圆于、和、,
易知当为轴时,取得最大值,
此时,
解得,
当轴时,取得最小值,
此时直线的方程为,
当,解得,
所以,
联立,解得,,
则椭圆的方程为;
证明:由知,,
不妨设直线的方程为,直线的方程为,其中,,
所以,
联立,
消去并整理得,
此时,
不妨设,,,
由韦达定理得,,
此时,,
所以,
同理得,
不妨设直线的斜率为,
此时,
则直线的方程为,
即,
因为,
所以,
则直线恒过定点,
而点与点到直线的距离之比,
故
第1页,共1页
同课章节目录
