2023-2024学年广东省佛山市桂城中学高二(下)第二次段考数学试卷(含答案)
文档属性
| 名称 | 2023-2024学年广东省佛山市桂城中学高二(下)第二次段考数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 44.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-03 15:41:07 | ||
图片预览


文档简介
2023-2024学年广东省佛山市桂城中学高二(下)第二次段考数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知随机变量,且,则( )
A. B. C. D.
2.一木块沿某一斜面自由下滑,测得下滑的水平距离与时间之间的函数关系式为,则时,此木块在水平方向的瞬时速度为( )
A. B. C. D.
3.已知数列满足,,则( )
A. B. C. D.
4.对于函数,下列说法错误的是( )
A. 有最小值但没有最大值
B. 对于任意的,恒有
C. 仅有一个零点
D. 有两个极值点
5.已知等差数列的前项和为,点,均在数列的图象上,则的最小值是( )
A. B. C. D.
6.今天的课外作业是从道应用题中任选题详细解答,则甲、乙两位同学的作业中恰有一题相同的概率是( )
A. B. C. D.
7.已知,则被除的余数为( )
A. B. C. D.
8.若过点可以作曲线的两条切线,则( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.若展开式中各奇数项的二项式系数的和为则( )
A. B. 展开式中各项的系数和为
C. 展开式中的常数项为 D. 展开式中的系数为
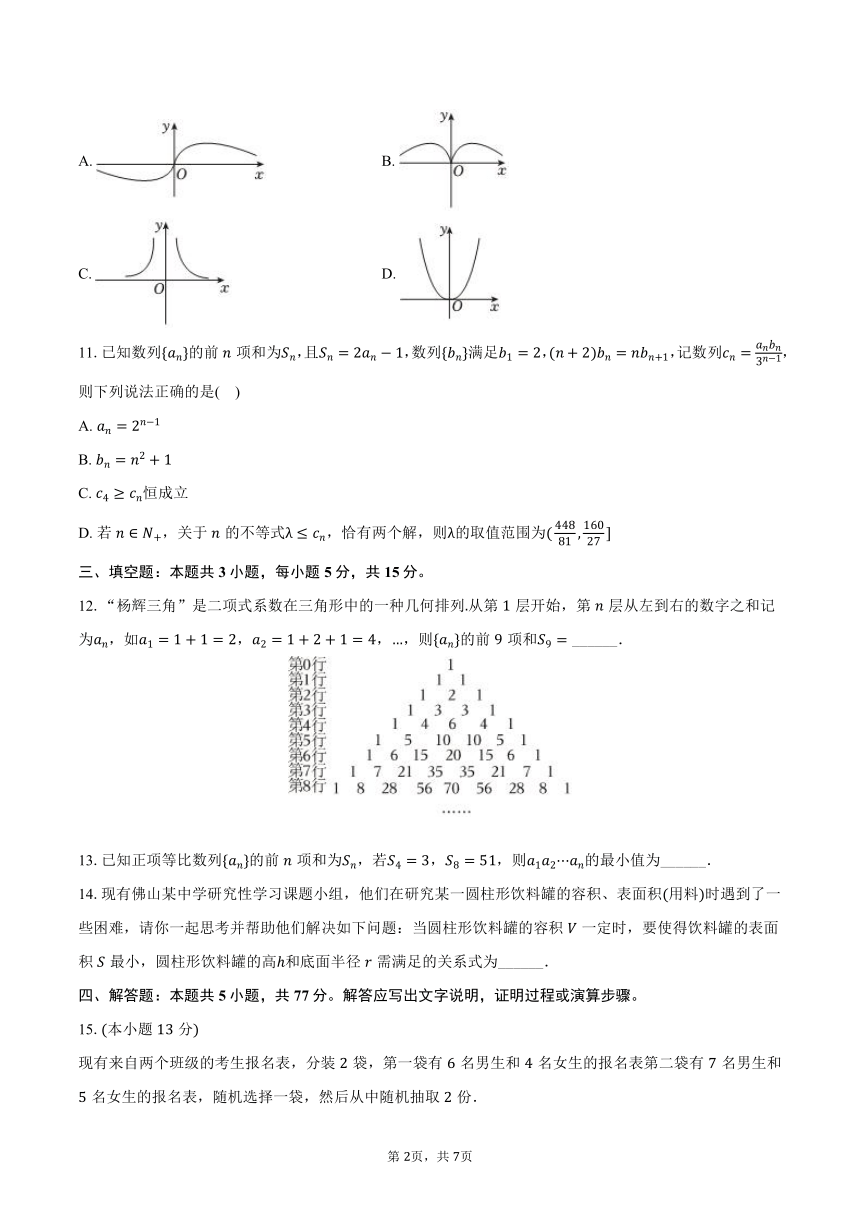
10.已知,函数的大致图象可能是( )
A. B.
C. D.
11.已知数列的前项和为,且,数列满足,,记数列,则下列说法正确的是( )
A.
B.
C. 恒成立
D. 若,关于的不等式,恰有两个解,则的取值范围为
三、填空题:本题共3小题,每小题5分,共15分。
12.“杨辉三角”是二项式系数在三角形中的一种几何排列从第层开始,第层从左到右的数字之和记为,如,,,则的前项和 ______.
13.已知正项等比数列的前项和为,若,,则的最小值为______.
14.现有佛山某中学研究性学习课题小组,他们在研究某一圆柱形饮料罐的容积、表面积用料时遇到了一些困难,请你一起思考并帮助他们解决如下问题:当圆柱形饮料罐的容积一定时,要使得饮料罐的表面积最小,圆柱形饮料罐的高和底面半径需满足的关系式为______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
现有来自两个班级的考生报名表,分装袋,第一袋有名男生和名女生的报名表第二袋有名男生和名女生的报名表,随机选择一袋,然后从中随机抽取份.
求恰好抽到男生和女生的报名表各份的概率;
若已知抽到的是男生和女生的报名表各份,用概率公式判断该报名表取自哪一袋的可能性更大.
16.本小题分
已知函数.
讨论的单调性;
若有个零点,求的取值范围.
17.本小题分
学生甲想加入校篮球队,篮球教练对其进行投篮测试测试规则如下:投篮分为两轮,每轮均有两次机会,第一轮在罚球线处,第二轮在三分线处;若他在罚球线处投进第一球,则直接进入下一轮,若第一次没投进可以进行第二次投篮,投进则进入下一轮,否则不预录取;若他在三分线处投进第一球,则直接录取,若第一次没投进可以进行第二次投篮,投进则录取,否则不予录取已知学生甲在罚球线处投篮命中率为,在三分线处投篮命中率为假设学生甲每次投进与否互不影响.
求学生甲被录取的概率;
在这次测试中,记学生甲投篮的次数为,求的分布列.
18.本小题分
已知数列满足,是公差为的等差数列.
求的通项公式.
令,求数列的前项和.
令,是否存在互不相等的正整数,,,使得,,成等差数列,且,,成等比数列?如果存在,请给出证明;如果不存在,请说明理由.
19.本小题分
已知函数,.
若,求曲线在点处的切线方程.
若,求的单调性.
当时,恒成立,求的取值范围.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:设“抽到第一袋”,“抽到第二袋”,“随机抽取份,恰好抽到男生和女生的报名表各份”,
则,,.
由全概率公式得.
报名表取自第一袋的概率.
报名表取自第二袋的概率.
因为,
所以该报名表取自第一袋的可能性更大.
16.解:,
当时,令,解得或,所以在和上单调递增,在上单调递减.
当时,恒成立,所以在上单调递增.
当时,令,解得或,所以在和上单调递增,在上单调递减.
由可知,又有个零点,所以,
,.
由,可得或,即的取值范围为.
17.解:记事件表示“甲在罚球线处投篮,第次投进”,事件表示“甲在三分线处投篮,第次投进”,
则,,
设事件表示“学生甲不被录取”,则,
所以,
所以学生甲被录取的概率为.
的可能取值为,,,
,
,
,
所以的分布列为:
18.解:由是公差为的等差数列,
得,且,则,
所以,所以,
解得.
由知,
所以.
.
由题意可知.
假设存在互不相等的正整数,,,使得,,成等差数列,且,,成等比数列,
则,,
即,,
化简得.
因为,当且仅当时,等号成立.
又因为,,互不相等,所以不存在互不相等的正整数,,.
19.解:因为,所以,则.
又,,
故曲线在点处的切线方程为,
即;
当时,所以,则.
令,,
则,.
当时,,单调递增,故,即;
当时,,单调递增,当时,,单调递减,
故,即.
从而在上恒成立,
则在上单调递增.
在上恒成立,
等价于在上恒成立.
若,则,
则显然成立;
若,则在上恒成立,
令,
由可知在上恒成立,
即在上单调递增;
故由可得,,
则,即.
令,则,
当时,,单调递减,
当时,,单调递增,
故H,故得.
综上所述,的取值范围为.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知随机变量,且,则( )
A. B. C. D.
2.一木块沿某一斜面自由下滑,测得下滑的水平距离与时间之间的函数关系式为,则时,此木块在水平方向的瞬时速度为( )
A. B. C. D.
3.已知数列满足,,则( )
A. B. C. D.
4.对于函数,下列说法错误的是( )
A. 有最小值但没有最大值
B. 对于任意的,恒有
C. 仅有一个零点
D. 有两个极值点
5.已知等差数列的前项和为,点,均在数列的图象上,则的最小值是( )
A. B. C. D.
6.今天的课外作业是从道应用题中任选题详细解答,则甲、乙两位同学的作业中恰有一题相同的概率是( )
A. B. C. D.
7.已知,则被除的余数为( )
A. B. C. D.
8.若过点可以作曲线的两条切线,则( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.若展开式中各奇数项的二项式系数的和为则( )
A. B. 展开式中各项的系数和为
C. 展开式中的常数项为 D. 展开式中的系数为
10.已知,函数的大致图象可能是( )
A. B.
C. D.
11.已知数列的前项和为,且,数列满足,,记数列,则下列说法正确的是( )
A.
B.
C. 恒成立
D. 若,关于的不等式,恰有两个解,则的取值范围为
三、填空题:本题共3小题,每小题5分,共15分。
12.“杨辉三角”是二项式系数在三角形中的一种几何排列从第层开始,第层从左到右的数字之和记为,如,,,则的前项和 ______.
13.已知正项等比数列的前项和为,若,,则的最小值为______.
14.现有佛山某中学研究性学习课题小组,他们在研究某一圆柱形饮料罐的容积、表面积用料时遇到了一些困难,请你一起思考并帮助他们解决如下问题:当圆柱形饮料罐的容积一定时,要使得饮料罐的表面积最小,圆柱形饮料罐的高和底面半径需满足的关系式为______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
现有来自两个班级的考生报名表,分装袋,第一袋有名男生和名女生的报名表第二袋有名男生和名女生的报名表,随机选择一袋,然后从中随机抽取份.
求恰好抽到男生和女生的报名表各份的概率;
若已知抽到的是男生和女生的报名表各份,用概率公式判断该报名表取自哪一袋的可能性更大.
16.本小题分
已知函数.
讨论的单调性;
若有个零点,求的取值范围.
17.本小题分
学生甲想加入校篮球队,篮球教练对其进行投篮测试测试规则如下:投篮分为两轮,每轮均有两次机会,第一轮在罚球线处,第二轮在三分线处;若他在罚球线处投进第一球,则直接进入下一轮,若第一次没投进可以进行第二次投篮,投进则进入下一轮,否则不预录取;若他在三分线处投进第一球,则直接录取,若第一次没投进可以进行第二次投篮,投进则录取,否则不予录取已知学生甲在罚球线处投篮命中率为,在三分线处投篮命中率为假设学生甲每次投进与否互不影响.
求学生甲被录取的概率;
在这次测试中,记学生甲投篮的次数为,求的分布列.
18.本小题分
已知数列满足,是公差为的等差数列.
求的通项公式.
令,求数列的前项和.
令,是否存在互不相等的正整数,,,使得,,成等差数列,且,,成等比数列?如果存在,请给出证明;如果不存在,请说明理由.
19.本小题分
已知函数,.
若,求曲线在点处的切线方程.
若,求的单调性.
当时,恒成立,求的取值范围.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:设“抽到第一袋”,“抽到第二袋”,“随机抽取份,恰好抽到男生和女生的报名表各份”,
则,,.
由全概率公式得.
报名表取自第一袋的概率.
报名表取自第二袋的概率.
因为,
所以该报名表取自第一袋的可能性更大.
16.解:,
当时,令,解得或,所以在和上单调递增,在上单调递减.
当时,恒成立,所以在上单调递增.
当时,令,解得或,所以在和上单调递增,在上单调递减.
由可知,又有个零点,所以,
,.
由,可得或,即的取值范围为.
17.解:记事件表示“甲在罚球线处投篮,第次投进”,事件表示“甲在三分线处投篮,第次投进”,
则,,
设事件表示“学生甲不被录取”,则,
所以,
所以学生甲被录取的概率为.
的可能取值为,,,
,
,
,
所以的分布列为:
18.解:由是公差为的等差数列,
得,且,则,
所以,所以,
解得.
由知,
所以.
.
由题意可知.
假设存在互不相等的正整数,,,使得,,成等差数列,且,,成等比数列,
则,,
即,,
化简得.
因为,当且仅当时,等号成立.
又因为,,互不相等,所以不存在互不相等的正整数,,.
19.解:因为,所以,则.
又,,
故曲线在点处的切线方程为,
即;
当时,所以,则.
令,,
则,.
当时,,单调递增,故,即;
当时,,单调递增,当时,,单调递减,
故,即.
从而在上恒成立,
则在上单调递增.
在上恒成立,
等价于在上恒成立.
若,则,
则显然成立;
若,则在上恒成立,
令,
由可知在上恒成立,
即在上单调递增;
故由可得,,
则,即.
令,则,
当时,,单调递减,
当时,,单调递增,
故H,故得.
综上所述,的取值范围为.
第1页,共1页
同课章节目录
