全等三角形教案
图片预览

文档简介
11.1 全等三角形
【教学目标】
1.知识与能力
理解全等三角形及相关概念,能够从图形中寻找全等三角形,探索并掌握全等三角形的性质,能够利用性质解决简单的问题.
2.过程与方法
在探索全等三角形性质的过程中,体会研究问题的方法,感受图形变化途径.
3.情感、态度与价值观
培养学生的识图能力、归纳总结能力和应用意识.
【教学重点】
(1)全等三角形以及相关概念.
(2)探索全等三角形的性质.
【教学难点】
不同情况下的三角形全等的图形归纳.
【教学方法】
创设情境-主体探究-合作交流-应用提高.
【教学过程】
一、创设情境,激发学生兴趣,引出本节要讨论的内容
活动1
观察出示的图形(教材中的图形),寻找形状大小相同的图形,归纳全等形的概念,进而得出全等三角形的概念.
全等形:能够完全重合的两个图形叫做全等形.
全等三角形:能够完全重合的两个三角形叫做全等三角形.
二、主体探究,合作交流,探究全等三角形的性质
活动2
△ABC与△DEF重合(电脑演示重合过程)
这时,点A与点D重合.点B与点E重合.我们把这样互相重合的一对点叫做对应顶点;AB边与DE边重合,这样互相重合的边就叫做对应边;∠A与∠D重合,它们就是对应角.△ABC与△DEF全等,我们把它记作:“△ABC≌△DEF”.读作“△ABC全等于△DEF”.
注意:记两个三角形全等时,通常把对应顶点的字母写在对应的位置上.
问题
你能找出其他的对应点、对应边和对应角吗?
点C与点F是对应点,BC边与EF边是对应边,CA边与FD边也是对应边.
∠B与∠E是对应角,∠C与∠F也是对应角.
活动3
问题
用两块全等的三角板重合放在桌面上,让其中一块绕一个顶点旋转,你能画出几种不同的位置关系,画出图形并说出对应元素.
学生活动设计:
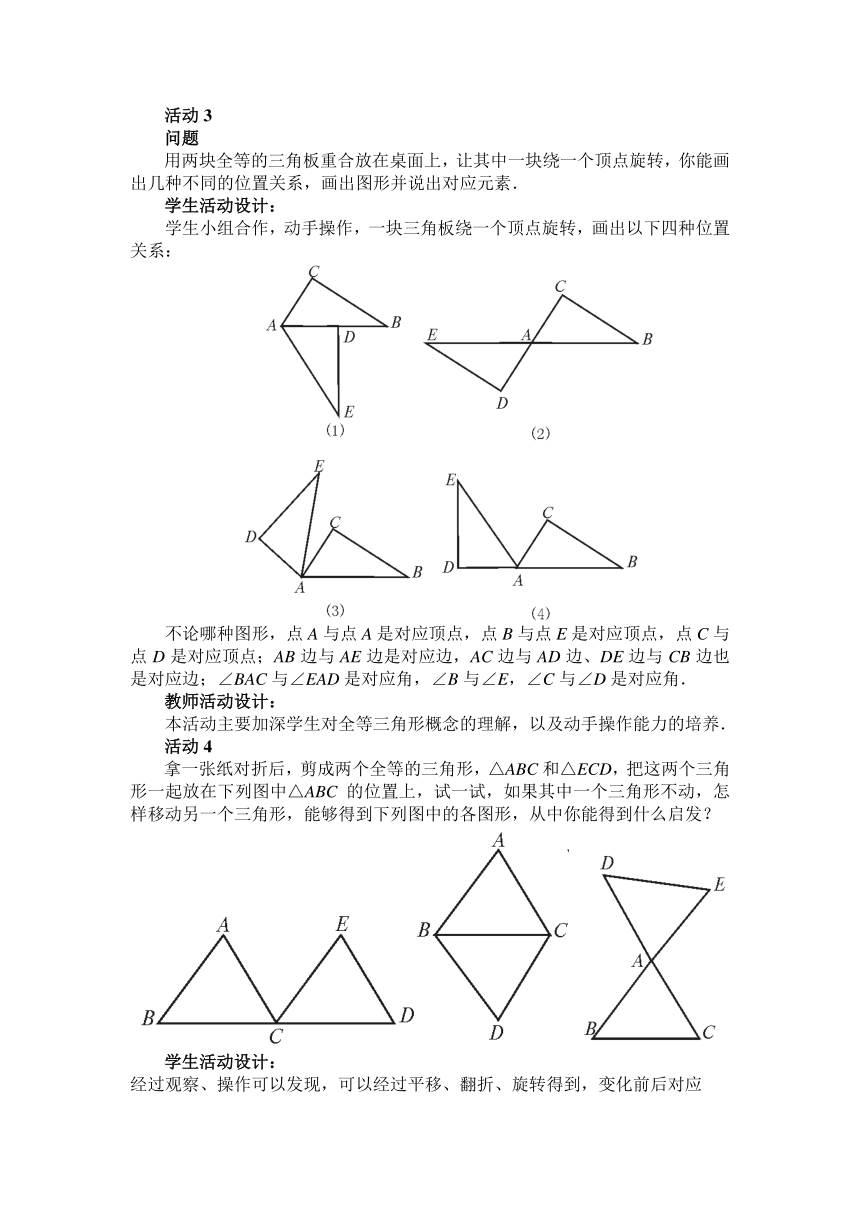
学生小组合作,动手操作,一块三角板绕一个顶点旋转,画出以下四种位置关系:
不论哪种图形,点A与点A是对应顶点,点B与点E是对应顶点,点C与点D是对应顶点;AB边与AE边是对应边,AC边与AD边、DE边与CB边也是对应边;∠BAC与∠EAD是对应角,∠B与∠E,∠C与∠D是对应角.
教师活动设计:
本活动主要加深学生对全等三角形概念的理解,以及动手操作能力的培养.
活动4
拿一张纸对折后,剪成两个全等的三角形,△ABC和△ECD,把这两个三角形一起放在下列图中△ABC的位置上,试一试,如果其中一个三角形不动,怎样移动另一个三角形,能够得到下列图中的各图形,从中你能得到什么启发?
( http: / / www. / Index.html ) ( http: / / www. / Index.html ) ( http: / / www. / Index.html )
学生活动设计:
经过观察、操作可以发现,可以经过平移、翻折、旋转得到,变化前后对应
角、对应边不变.
教师活动设计:
组织学生观察、归纳,引导学生归纳全等三角形的性质:
全等三角形的对应边相等.
全等三角形的对应角相等.
三、拓展创新、应用提高,培养学生的创新意识和应用能力
问题
如图,△ABC≌△AEC,∠B=30°,∠ACB=85°.求出△AEC各内角的度数.
(学生根据全等三角形的性质独立解决.)
解:在△ABC中,已知∠ACB=85°,∠B=30°,根据三角形的内角和等于180°,可得:∠BAC=65°.
因为△ABC≌△AEC,所以∠EAC=∠BAC=65°,∠E=∠B=30°,∠ACE=∠ACB=85°.
答:△AEC的内角的度数分别为65°、30°、85°.
问题
如图是一个等边三角形,你能利用折纸的方法把它分成两个全等的三角形吗?你能把它分成三个,四个全等的三角形吗?
学生活动设计:
学生小组讨论,经过讨论交流自己的方法。可能有下列方法:
四、归纳小结、布置作业
小结:
1.全等形、全等三角形及相关概念.
2.全等三角形的性质.
【教学目标】
1.知识与能力
理解全等三角形及相关概念,能够从图形中寻找全等三角形,探索并掌握全等三角形的性质,能够利用性质解决简单的问题.
2.过程与方法
在探索全等三角形性质的过程中,体会研究问题的方法,感受图形变化途径.
3.情感、态度与价值观
培养学生的识图能力、归纳总结能力和应用意识.
【教学重点】
(1)全等三角形以及相关概念.
(2)探索全等三角形的性质.
【教学难点】
不同情况下的三角形全等的图形归纳.
【教学方法】
创设情境-主体探究-合作交流-应用提高.
【教学过程】
一、创设情境,激发学生兴趣,引出本节要讨论的内容
活动1
观察出示的图形(教材中的图形),寻找形状大小相同的图形,归纳全等形的概念,进而得出全等三角形的概念.
全等形:能够完全重合的两个图形叫做全等形.
全等三角形:能够完全重合的两个三角形叫做全等三角形.
二、主体探究,合作交流,探究全等三角形的性质
活动2
△ABC与△DEF重合(电脑演示重合过程)
这时,点A与点D重合.点B与点E重合.我们把这样互相重合的一对点叫做对应顶点;AB边与DE边重合,这样互相重合的边就叫做对应边;∠A与∠D重合,它们就是对应角.△ABC与△DEF全等,我们把它记作:“△ABC≌△DEF”.读作“△ABC全等于△DEF”.
注意:记两个三角形全等时,通常把对应顶点的字母写在对应的位置上.
问题
你能找出其他的对应点、对应边和对应角吗?
点C与点F是对应点,BC边与EF边是对应边,CA边与FD边也是对应边.
∠B与∠E是对应角,∠C与∠F也是对应角.
活动3
问题
用两块全等的三角板重合放在桌面上,让其中一块绕一个顶点旋转,你能画出几种不同的位置关系,画出图形并说出对应元素.
学生活动设计:
学生小组合作,动手操作,一块三角板绕一个顶点旋转,画出以下四种位置关系:
不论哪种图形,点A与点A是对应顶点,点B与点E是对应顶点,点C与点D是对应顶点;AB边与AE边是对应边,AC边与AD边、DE边与CB边也是对应边;∠BAC与∠EAD是对应角,∠B与∠E,∠C与∠D是对应角.
教师活动设计:
本活动主要加深学生对全等三角形概念的理解,以及动手操作能力的培养.
活动4
拿一张纸对折后,剪成两个全等的三角形,△ABC和△ECD,把这两个三角形一起放在下列图中△ABC的位置上,试一试,如果其中一个三角形不动,怎样移动另一个三角形,能够得到下列图中的各图形,从中你能得到什么启发?
( http: / / www. / Index.html ) ( http: / / www. / Index.html ) ( http: / / www. / Index.html )
学生活动设计:
经过观察、操作可以发现,可以经过平移、翻折、旋转得到,变化前后对应
角、对应边不变.
教师活动设计:
组织学生观察、归纳,引导学生归纳全等三角形的性质:
全等三角形的对应边相等.
全等三角形的对应角相等.
三、拓展创新、应用提高,培养学生的创新意识和应用能力
问题
如图,△ABC≌△AEC,∠B=30°,∠ACB=85°.求出△AEC各内角的度数.
(学生根据全等三角形的性质独立解决.)
解:在△ABC中,已知∠ACB=85°,∠B=30°,根据三角形的内角和等于180°,可得:∠BAC=65°.
因为△ABC≌△AEC,所以∠EAC=∠BAC=65°,∠E=∠B=30°,∠ACE=∠ACB=85°.
答:△AEC的内角的度数分别为65°、30°、85°.
问题
如图是一个等边三角形,你能利用折纸的方法把它分成两个全等的三角形吗?你能把它分成三个,四个全等的三角形吗?
学生活动设计:
学生小组讨论,经过讨论交流自己的方法。可能有下列方法:
四、归纳小结、布置作业
小结:
1.全等形、全等三角形及相关概念.
2.全等三角形的性质.
