第十八章 平行四边形检测卷2023—2024学年人教版数学八年级下册(含答案)
文档属性
| 名称 | 第十八章 平行四边形检测卷2023—2024学年人教版数学八年级下册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 412.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-03 20:01:12 | ||
图片预览

文档简介
第十八章平行四边形检测卷
(90分钟 120分)
一、选择题(本大题10 小题,每小题3分,共30分)
1.下面的性质中,平行四边形不一定具有的是 ( )
A.对角互补 B.邻角互补 C.对角相等 D.对边相等
2.如图,在 ABCD中,对角线 AC,BD 交于点O,点 E是AB 的中点.若 OE=3cm,则 BC的长为( )
A. 3cm B.6 cm C.9 cm D.12 cm
3.在□ABCD中,∠A:∠B:∠C:∠D的值可以是 ( )
A.1: 2: 3: 4 B.1: 2:2:1 C.2:2:1:1 D.2: 1: 2:1
4.在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是某合作学习小组的4位同学拟订的方案,其中正确的是 ( )
A.测量其中三个角是否都为直角 B.测量两组对边是否分别相等
C.测量一组对角是否都为直角 D.测量对角线是否相互平分
5.如图,EF 过矩形ABCD 对角线的交点O,且分别交AB,CD于点E,F,那么阴影部分的面积是矩形ABCD 面积的 ( )
A. B. C. D.
6.用两块完全相同的直角三角形拼下列图形:①平行四边形;②矩形;③菱形;④正方形;⑤等腰三角形;⑥等边三角形.一定能拼成的图形是 ( )
A.①④⑤ B.②⑤⑥ C.①②③ D.①②⑤
7.如图,在菱形ABCD中,AC=6 cm,BD=8cm,则菱形 AB边上的高CE 的长是 ( )
B. /s cm C. 5cm D.10 cm
8.下列说法错误的是 ( )
A.一组对边平行且一组对角相等的四边形是平行四边形
B.每组邻边都相等的四边形是菱形
C.对角线互相垂直的平行四边形是正方形
D.四个角都相等的四边形是矩形
9.在四边形ABCD中,AC,BD相交于点O,能判定这个四边形是正方形的条件是 ( )
A. OA=OB=OC=OD,AC⊥BD B. AB∥CD,AC=BD
中小学教育资源及组卷应用平台
C. AD∥BC,∠A=∠C D. OA=OC,OB=OD,AB=BC
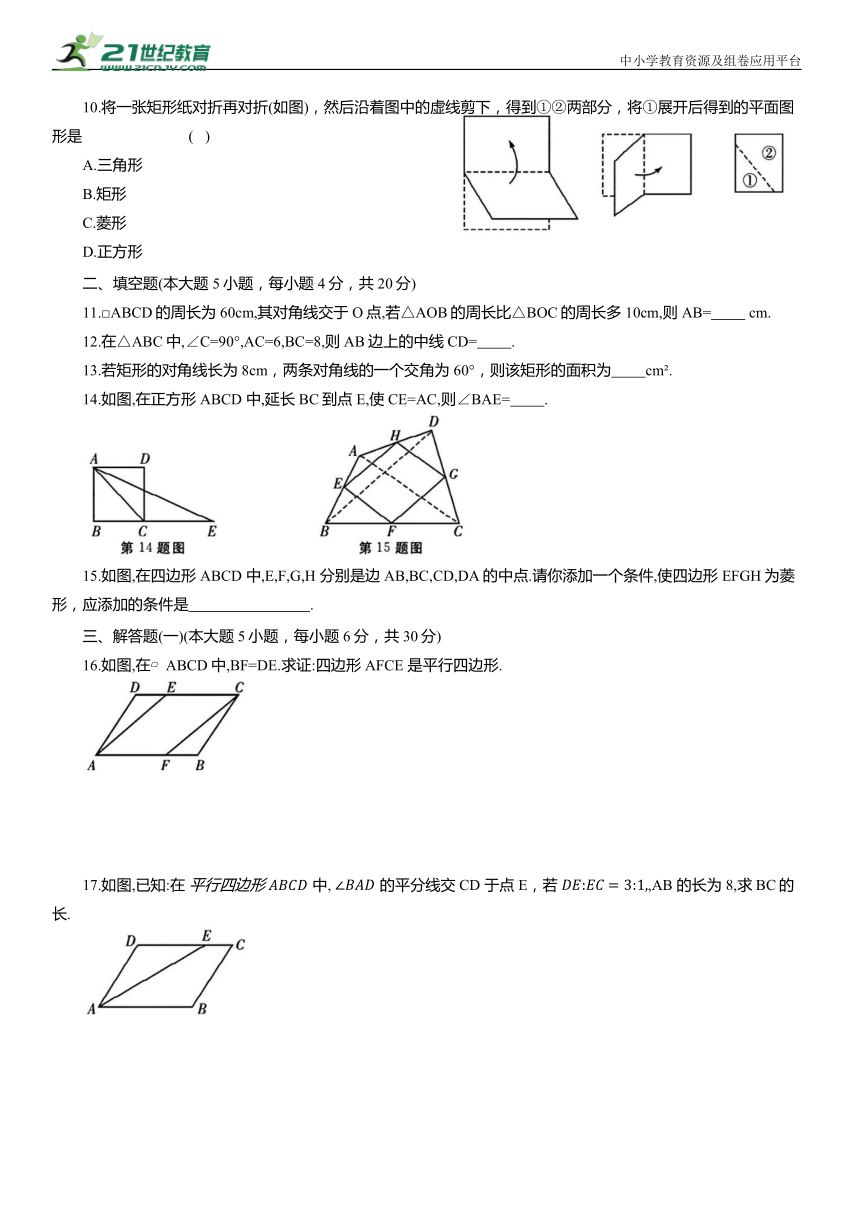
10.将一张矩形纸对折再对折(如图),然后沿着图中的虚线剪下,得到①②两部分,将①展开后得到的平面图形是 ( )
A.三角形
B.矩形
C.菱形
D.正方形
二、填空题(本大题5小题,每小题4分,共20分)
11.□ABCD的周长为60cm,其对角线交于O点,若△AOB的周长比△BOC的周长多10cm,则AB= cm.
12.在△ABC中,∠C=90°,AC=6,BC=8,则AB边上的中线CD= .
13.若矩形的对角线长为8cm,两条对角线的一个交角为 60°,则该矩形的面积为 cm .
14.如图,在正方形 ABCD 中,延长BC到点E,使CE=AC,则∠BAE= .
15.如图,在四边形 ABCD 中,E,F,G,H 分别是边AB,BC,CD,DA的中点.请你添加一个条件,使四边形 EFGH为菱形,应添加的条件是 .
三、解答题(一)(本大题5小题,每小题6分,共30分)
16.如图,在 ABCD中,BF=DE.求证:四边形AFCE 是平行四边形.
17.如图,已知:在 中, 的平分线交CD 于点E,若 ,AB 的长为8,求BC的长.
18.已知:如图, 的对角线AC,BD 相交于点O,且. .求证:四边形ABCD是矩形.
C
19.如图,已知平行四边形中, .证明:四边形 DEBF为平行四边形.
20.如图,在平行四边形中,M是CD 的中点,且. .求证:四边形ABCD是矩形.
B
四、解答题(二)(本大题5小题,每小题8分,共40分)
21.如图,在正方形 ABCD中, ,AF 交对角线 BD 于点 E,交 CD 于点 F.求 的度数.
C
22.如图,在菱形ABCD 中,周长为8cm, ,对角线 AC,BD交于点O.求这个菱形的对角线长和面积.
D
23.如图,E,F是 ABCD的对角线AC上的两点,CE=AF.请猜想:BE 与DF 有怎样的位置关系和数量关系 并对你的猜想加以证明.
24.已知:如图,在△ABC中,∠C=90°,CD平分∠ACB,DE⊥BC于点E,DF⊥AC于点F.
求证:四边形 CFDE 是正方形.
25.如图,△ABC为等边三角形,D,F 分别是BC,AB上的点,且CD=BF,以 AD 为边作等边三角形ADE.
(1)求证:△ACD≌△CBF;
(2)当D在线段BC上何处时,四边形 CDEF 为平行四边形,且∠DEF=30° 证明你的结论.
1. A 2. B 3. D 4. A 5. B 6. D 7. A 8. C 9. A10. C 11.20 12.5 13.16 14.67.5°
15. AC=BD
16.提示:易证CE∥AF,CE=AF,∴四边形 AFCE是平行四边形.
17.6
18.证明:∵∠DBC=∠ACB,∴OB=OC.
易证AC=BD,∴四边形ABCD 是矩形.
19.提示:证△ADE≌△CBF(AAS).易得 DE∥BF,DE=BF,∴四边形 DEBF为平行四边形.
20.提示:证△ADM≌△BCM(SSS).易得∠D=90°,∴四边形ABCD是矩形.
21.70°
22.提示:易求AB=2,OA=1,OB= ,
∴AC=2,BD=2 ,S=2 .
23.猜想 BE∥DF,BE=DF.证明略.
24.提示:易证四边形CFDE是矩形,再证 DF=DE,∴四边形 CFDE 是正方形.
25.(1)证明:∵等边三角形ABC,∴AC=CB,∠ABC=∠ACB.又∵CD=BF,∴△ACD≌△CBF.
(2)D 为BC 中点时满足条件(证明略).
(90分钟 120分)
一、选择题(本大题10 小题,每小题3分,共30分)
1.下面的性质中,平行四边形不一定具有的是 ( )
A.对角互补 B.邻角互补 C.对角相等 D.对边相等
2.如图,在 ABCD中,对角线 AC,BD 交于点O,点 E是AB 的中点.若 OE=3cm,则 BC的长为( )
A. 3cm B.6 cm C.9 cm D.12 cm
3.在□ABCD中,∠A:∠B:∠C:∠D的值可以是 ( )
A.1: 2: 3: 4 B.1: 2:2:1 C.2:2:1:1 D.2: 1: 2:1
4.在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是某合作学习小组的4位同学拟订的方案,其中正确的是 ( )
A.测量其中三个角是否都为直角 B.测量两组对边是否分别相等
C.测量一组对角是否都为直角 D.测量对角线是否相互平分
5.如图,EF 过矩形ABCD 对角线的交点O,且分别交AB,CD于点E,F,那么阴影部分的面积是矩形ABCD 面积的 ( )
A. B. C. D.
6.用两块完全相同的直角三角形拼下列图形:①平行四边形;②矩形;③菱形;④正方形;⑤等腰三角形;⑥等边三角形.一定能拼成的图形是 ( )
A.①④⑤ B.②⑤⑥ C.①②③ D.①②⑤
7.如图,在菱形ABCD中,AC=6 cm,BD=8cm,则菱形 AB边上的高CE 的长是 ( )
B. /s cm C. 5cm D.10 cm
8.下列说法错误的是 ( )
A.一组对边平行且一组对角相等的四边形是平行四边形
B.每组邻边都相等的四边形是菱形
C.对角线互相垂直的平行四边形是正方形
D.四个角都相等的四边形是矩形
9.在四边形ABCD中,AC,BD相交于点O,能判定这个四边形是正方形的条件是 ( )
A. OA=OB=OC=OD,AC⊥BD B. AB∥CD,AC=BD
中小学教育资源及组卷应用平台
C. AD∥BC,∠A=∠C D. OA=OC,OB=OD,AB=BC
10.将一张矩形纸对折再对折(如图),然后沿着图中的虚线剪下,得到①②两部分,将①展开后得到的平面图形是 ( )
A.三角形
B.矩形
C.菱形
D.正方形
二、填空题(本大题5小题,每小题4分,共20分)
11.□ABCD的周长为60cm,其对角线交于O点,若△AOB的周长比△BOC的周长多10cm,则AB= cm.
12.在△ABC中,∠C=90°,AC=6,BC=8,则AB边上的中线CD= .
13.若矩形的对角线长为8cm,两条对角线的一个交角为 60°,则该矩形的面积为 cm .
14.如图,在正方形 ABCD 中,延长BC到点E,使CE=AC,则∠BAE= .
15.如图,在四边形 ABCD 中,E,F,G,H 分别是边AB,BC,CD,DA的中点.请你添加一个条件,使四边形 EFGH为菱形,应添加的条件是 .
三、解答题(一)(本大题5小题,每小题6分,共30分)
16.如图,在 ABCD中,BF=DE.求证:四边形AFCE 是平行四边形.
17.如图,已知:在 中, 的平分线交CD 于点E,若 ,AB 的长为8,求BC的长.
18.已知:如图, 的对角线AC,BD 相交于点O,且. .求证:四边形ABCD是矩形.
C
19.如图,已知平行四边形中, .证明:四边形 DEBF为平行四边形.
20.如图,在平行四边形中,M是CD 的中点,且. .求证:四边形ABCD是矩形.
B
四、解答题(二)(本大题5小题,每小题8分,共40分)
21.如图,在正方形 ABCD中, ,AF 交对角线 BD 于点 E,交 CD 于点 F.求 的度数.
C
22.如图,在菱形ABCD 中,周长为8cm, ,对角线 AC,BD交于点O.求这个菱形的对角线长和面积.
D
23.如图,E,F是 ABCD的对角线AC上的两点,CE=AF.请猜想:BE 与DF 有怎样的位置关系和数量关系 并对你的猜想加以证明.
24.已知:如图,在△ABC中,∠C=90°,CD平分∠ACB,DE⊥BC于点E,DF⊥AC于点F.
求证:四边形 CFDE 是正方形.
25.如图,△ABC为等边三角形,D,F 分别是BC,AB上的点,且CD=BF,以 AD 为边作等边三角形ADE.
(1)求证:△ACD≌△CBF;
(2)当D在线段BC上何处时,四边形 CDEF 为平行四边形,且∠DEF=30° 证明你的结论.
1. A 2. B 3. D 4. A 5. B 6. D 7. A 8. C 9. A10. C 11.20 12.5 13.16 14.67.5°
15. AC=BD
16.提示:易证CE∥AF,CE=AF,∴四边形 AFCE是平行四边形.
17.6
18.证明:∵∠DBC=∠ACB,∴OB=OC.
易证AC=BD,∴四边形ABCD 是矩形.
19.提示:证△ADE≌△CBF(AAS).易得 DE∥BF,DE=BF,∴四边形 DEBF为平行四边形.
20.提示:证△ADM≌△BCM(SSS).易得∠D=90°,∴四边形ABCD是矩形.
21.70°
22.提示:易求AB=2,OA=1,OB= ,
∴AC=2,BD=2 ,S=2 .
23.猜想 BE∥DF,BE=DF.证明略.
24.提示:易证四边形CFDE是矩形,再证 DF=DE,∴四边形 CFDE 是正方形.
25.(1)证明:∵等边三角形ABC,∴AC=CB,∠ABC=∠ACB.又∵CD=BF,∴△ACD≌△CBF.
(2)D 为BC 中点时满足条件(证明略).
