第十九章 一次函数课时强化训练 2023—2024学年人教版数学八年级下册(含答案)
文档属性
| 名称 | 第十九章 一次函数课时强化训练 2023—2024学年人教版数学八年级下册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1002.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-03 20:09:30 | ||
图片预览


文档简介
第十九章 一次函数
19.1 函数
中小学教育资源及组卷应用平台
第1 课时 变量与函数
1.函数 中,自变量x的取值范围是( )
A.x≤-5 B. x≠-5
C. x> -5 D.x≥-5
2.某居民小区收取电费的标准是0.6 元/千瓦时,当用电量为x(单位:千瓦时)时,收取电费为y(单位:元).在这个问题中,下列说法中正确的是 ( )
A.x是自变量,0.6元/千瓦时是因变量
B.y是自变量,x是因变量
C.0.6 元/千瓦时是自变量,y是因变量
D.x是自变量,y是因变量
3.下列各式①y=0.5x-2;②y=|2x|;③3y+5=x; 中,y是x的函数的有 (只填序号).
4.某市出租车收费按里程计算,3 千米以内(含3千米)收费10 元,超过3千米,每增加1 千米加收2元,则当x≥3时,车费y(单位:元)与x(单位:千米)之间的关系式为 .
5.冷冻一个20℃的物体,若它每小时下降2℃,则物体的温度 T(单位:℃)与冷冻时间t(单位:时)的关系式是 .
6.设路程为s km,速度为v km/h,时间th,指出下列各式中的常量与变量.
7.当x=2及x=-3时,分别求出下列函数的函数值:
(1)y=(x+1)(x-2);
8.如图,梯形上底的长是x,下底的长是15,高是8.
(1)梯形面积y与上底长x之间的关系式是什么
(2)用表格表示当x从10变到16时(每次增加1),y的相应值;
x 10 11 12 13 14 15 16
y
(3)当x每增加1时,y如何变化
(4)当x=0时,y等于什么 此时它表示的是什么
9.已知水池中有800 m 的水,每小时抽出50 m .
(1)写出剩余水的体积Q(单位:m )与时间t(单位:h)之间的函数关系式;
(2)6 h后池中还有多少水
(3)多少小时后,池中还有200 m 的水
第2 课时 i函数的图象
1.下面说法中正确的是 ( )
A.两个变量间的关系只能用关系式表示
B.图象不能直观的表示两个变量间的数量关系
C.借助表格可以表示出因变量随自变量的变化情况
D.以上说法都不对
2.1-6 个月的婴儿生长发育得非常快,出生体重为4000克的婴儿,他们的体重y(单位:克)和月龄x(单位:月)之间的关系如下表,则6个月大的婴儿的体重为 ( )
月龄/月 1 2 3 4 5
体重/克 4 700 5 400 6 100 6800 7 500
A.7 600 克 B.7 800 克
C.8 200 克 D.8 500 克
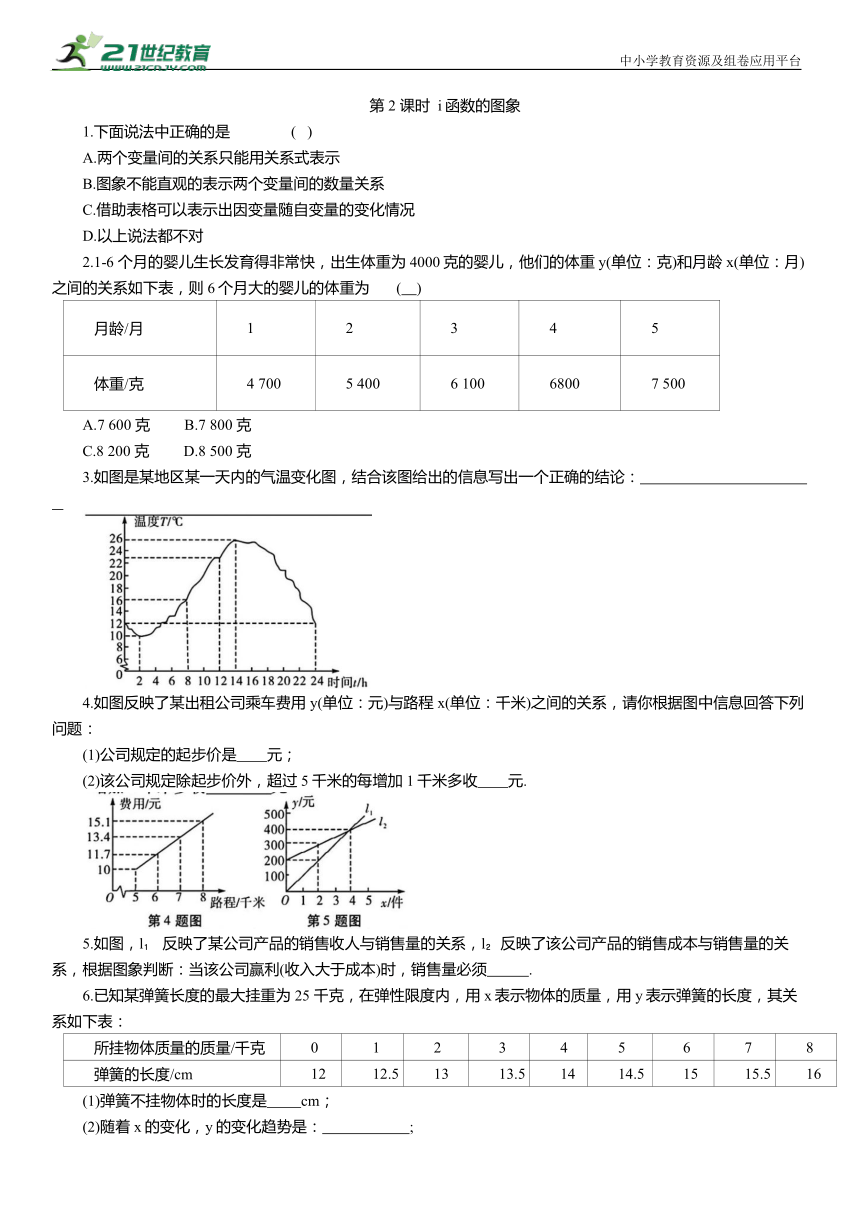
3.如图是某地区某一天内的气温变化图,结合该图给出的信息写出一个正确的结论:
4.如图反映了某出租公司乘车费用y(单位:元)与路程x(单位:千米)之间的关系,请你根据图中信息回答下列问题:
(1)公司规定的起步价是 元;
(2)该公司规定除起步价外,超过5千米的每增加1千米多收 元.
5.如图,l 反映了某公司产品的销售收人与销售量的关系,l 反映了该公司产品的销售成本与销售量的关系,根据图象判断:当该公司赢利(收入大于成本)时,销售量必须 .
6.已知某弹簧长度的最大挂重为25 千克,在弹性限度内,用x表示物体的质量,用y表示弹簧的长度,其关系如下表:
所挂物体质量的质量/千克 0 1 2 3 4 5 6 7 8
弹簧的长度/cm 12 12.5 13 13.5 14 14.5 15 15.5 16
(1)弹簧不挂物体时的长度是 cm;
(2)随着x的变化,y的变化趋势是: ;
(3)根据表中数据的变化关系,写出y与x的关系式,并指出自变量的取值范围是 :
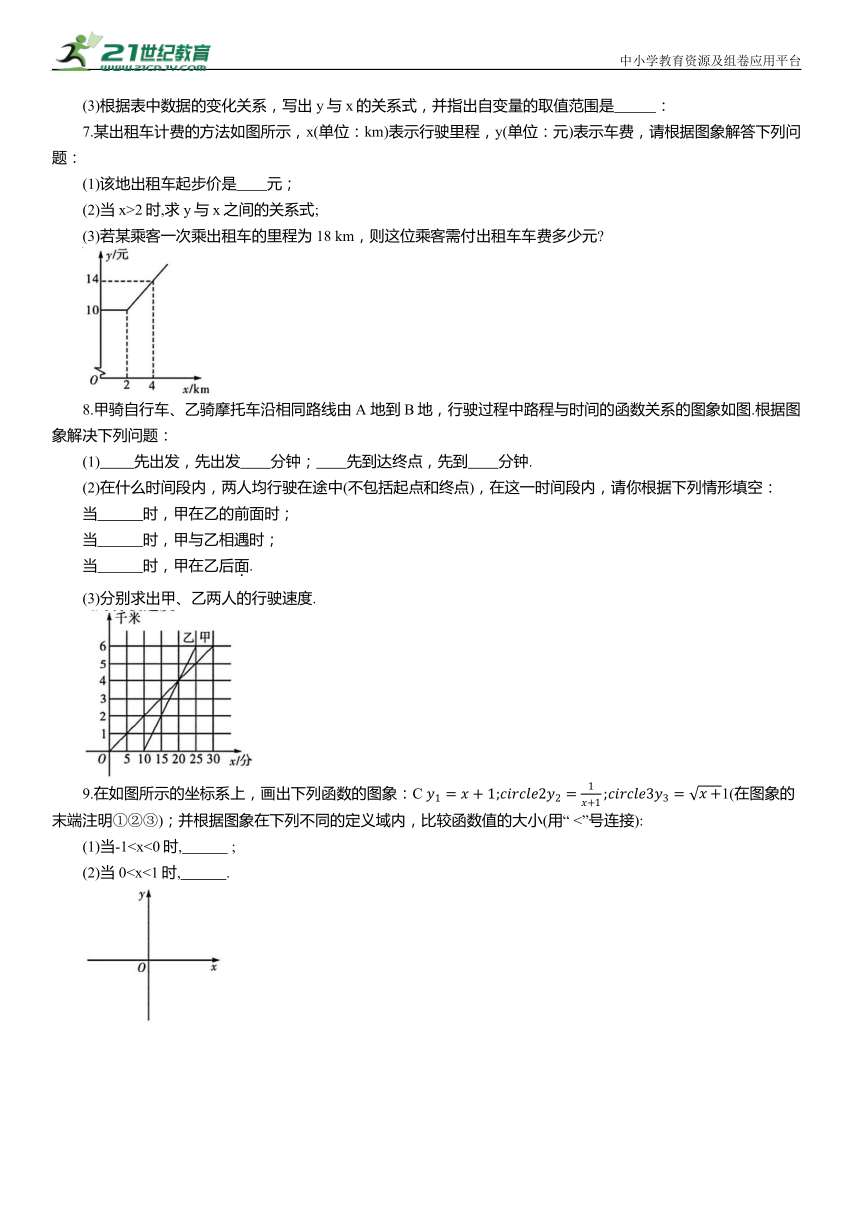
7.某出租车计费的方法如图所示,x(单位:km)表示行驶里程,y(单位:元)表示车费,请根据图象解答下列问题:
(1)该地出租车起步价是 元;
(2)当x>2时,求y与x之间的关系式;
(3)若某乘客一次乘出租车的里程为18 km,则这位乘客需付出租车车费多少元
8.甲骑自行车、乙骑摩托车沿相同路线由 A 地到B地,行驶过程中路程与时间的函数关系的图象如图.根据图象解决下列问题:
(1) 先出发,先出发 分钟; 先到达终点,先到 分钟.
(2)在什么时间段内,两人均行驶在途中(不包括起点和终点),在这一时间段内,请你根据下列情形填空:
当 时,甲在乙的前面时;
当 时,甲与乙相遇时;
当 时,甲在乙后面.
(3)分别求出甲、乙两人的行驶速度.
9.在如图所示的坐标系上,画出下列函数的图象:C 1(在图象的末端注明①②③);并根据图象在下列不同的定义域内,比较函数值的大小(用“ <”号连接):
(1)当-1(2)当019.2 一次函数
第 1 课时正比例函数
1.已知函数y=(a-1)x的图象过第一、三象限,那么a的取值范围是 ( )
A. a>1 B. a<1 C. a>0 D. a<0
2.在平面直角坐标系中,正比例函数 y =-3x的图象的大体位置是 ( )
3.已知函数y=(k-3)x,y随x的增大而减小,则常数 k的取值范围是 ( )
A. k>3 B. k<3
C. k<-3 D. k<0
4.已知函数 是正比例函数,则m= .
5.在函数 中,若自变量x的取值范围是50≤x≤75,则函数值 y 的取值范 围为
6.下列函数哪些是正比例函数 是正比例函数的指出比例系数.
(1)y=-4x;(2)y=3x-1;(3)y= x;(4)y= ;
7.已知函数y=(k+3)x.
(1)k为何值时,函数为正比例函数;
(2)k为何值时,函数的图象经过第一、三象限;
(3)k为何值时,y随x的增大而减小
(4)k为何值时,函数图象经过点(1,1)
8.(1)在同一平面直角坐标系内画出正比例函数 与 的图象;
(2)请你用量角器度量一下这两条直线的交角,你会发现什么 写出你的猜想.
当m 为何值时,正比例函数 的图象在哪几个象限y随x的增大而减小
第2课时 一次函数的概念
1.下列函数不是一次函数的是 ( )
C. y= -x+1
2.函数y=(m-1)x+2-m是一次函数,则m满足的条件是 ,若此函数是正比例函数,则 m= .
3.已知 是一次函数,则k= .
4.函数 是一次函数,m,n 应满足的条件是 .
5.一般地,海拔高度每上升1 km,温度下降6℃.某时刻测量某市地面温度为20℃.设高出地面xkm处的温度为y℃,则y与x的函数关系式为 ,y x的一次函数.(填“是”或“不是”)
6.一个小球由静止开始从一个斜坡向下滚动,其速度每秒增加2 米.
(1)求这个小球速度v随时间t变化的函数关系.它是一次函数吗
(2)求第2.5 秒时小球的速度.
7.已知 是一次函数.
(1)求k的值;
(2)求x=3时,y的值;
(3)当y=0时,x的值.
8.写出下列各题中x与y之间的解析式,并判断y是否是x的一次函数.
(1)在时速为70 千米的匀速运动中,路程y(单位:千米)与时间(单位:小时)的关系;
(2)居民用电标准是每千瓦时0.53 元,则电费y(单位:元)与用电量x(单位:千瓦时)之间的关系;
(3)汽车离开A站4千米,再以40千米/时的平均速度行驶了x小时,那么汽车离开 A站的距离y(单位:千米)与时间(单位:小时)之间的关系;
(4)某车站规定旅客可以免费携带不超过20千克的行李,超过部分每千克收取1.5 元的行李费用,则旅客需交的行李费y(单位:元)与携带行李重量x(单位:千克)之间的关系.
9.已知y+a与x-b成正比例(其中a,b都是常数).
(1)试说明y是x的一次函数;
(2)如果x=-1时,y=-15;x=7时,y=1,求这个一次函数的解析式.
第3课时 一次函数的图象与性质
1.一次函数y =kx+b的图象如图所示,则k,b的值为( )
A. k<0,b<0
B. k<0,b>0
C. k>0,b<0
D. k>0,b>0
2.关于函数y=-2x+1,下列结论正确的是( )
A.图象必经过点( -2,1)
B. y随x的增大而增大
C.图象经过第一、二、三象限
D.当 时,y<0
3.一次函数y=(2m-1)x+1,若y随x的增大而增大,则m的取值范围是 .
4.关于x的一次函数 的图象可能正确的是 .
5.把函数y=-3x的图象向上平移2 个单位长度所得图象的解析式是 .
6.已知函数y=-x+4,回答下列问题:
(1)请在下图的直角坐标系中画出函数y=-x+4的图象;
(2)y随x的增大而 ;
(3)当y=2时,x的值为 ;
(4)当y<0时,x的取值范围是 .
7.已知一次函数y=(2m+4)x+(3-n),求:
(1)当m为何值时,y随x的增大而增大;
(2)当n为何值时,函数图象与y轴的交点在x轴下方;
(3)m,n 为何值时,函数图象过原点.
8.已知一次函数
(1)k为何值时,它的图象经过原点;
(2)k为何值时,它的图象经过点(0,-2);
(3)k为何值时,它的图象平行于直线y=-x.
(4)若这个函数是一次函数,且y随x的增大而减小,求k的取值范围.
9.已知一次函数y=2x+4.
(1)在如图所示的平面直角坐标系中,画出函数的图象;
(2)求图象与坐标轴所围成图形的面积;
(3)利用图象直接写出:当y<0时,x的取值范围.
第4 课时 求一次函数的解析式
1.如图,直线 AB 对应的函数解析式是 ( )
2.若直线l与直线y=3x+1关于y轴对称,则直线l的解析式为( )
A. y= -3x-1 B. y= -3x+1
C. y=3x-1 D. y= -x+1
3.已知y与x+1 成正比例,比例系数是2,则y与x的函数关系式是 .
4.如果函数y=4x+3-k的图象经过原点,那么k= .
5.已知一次函数的图象与直线y=-x+1 平行,且过点(8,2),则此一次函数的解析式为
6.在平面直角坐标系中,直线y=kx+b经过点A(1,1)和点B( -3,5).
(1)求直线AB 所对应的函数解析式;
(2)判断点(4,-2)是否在直线AB 上.
7.已知:y+2 与x-3 成正比例,且当x=5时,y=2.
(1)求y与x之间的函数解析式;
(2)当y=4时,x的值是多少.
8.如图,在平面直角坐标系xOy中,已知点A(0,8),B(6,0),点C(3,a)在线段AB 上.
(1)则a的值为 ;
(2)若点 D( -4,3),求直线 CD 的函数解析式;
(3)点(-5,-4)在直线 CD 上吗 说明理由.
9.如图,已知直线 交x轴于点A,交y轴于点 B.
(1)求A,B两点的坐标;
(2)已知点 C 是线段 AB 上的一点,当S△AOC= 时,求直线OC 的解析式.
第5课时 一次函数的应用
1.某次大型活动,组委会启用无人机航拍活动过程,在操控无人机时应根据现场状况调节高度,已知无人机在上升和下降过程中速度相同,设无人机的飞行高度为y(单位:米),操控无人机的时间为x(单位:分),y与x之间的函数图象如图所示.
(1)无人机的速度为 米/分;
(2)求线段BC 所表示的y与x之间函数表达式;
(3)无人机在 50 米上空持续飞行时间为 分钟.
2.小越为湖州某校食堂王经理建议食堂就餐情况,经调查发现就餐时,有520 人排队吃饭就餐,就餐开始后仍有学生继续前来排队进食堂.设学生按固定的速度增加,食堂打饭窗口打饭菜的速度也是固定的.若每分钟该食堂新增排队学生数12 人,每个打饭窗口每分钟打饭菜10 人.已知食堂的前a 分钟只开放了两个打饭窗口;某一天食堂排队等候的学生数y(单位:人)与打饭菜时间x(单位:分钟)的关系如图所示.
(1)求a的值;
(2)求排队到第16 分钟时,食堂排队等候打饭菜的学生人数;
(3)若要在开始打饭菜后8 分钟内让所有排队的学生都能进食堂后来到食堂窗口的学生随到随吃,那么小赵应该建议食堂王经理一开始就需要至少同时开放几个打饭窗口
3.某校去年购买了A,B 两种足球,费用分别为2 400 元和2 000 元,其中A 种足球数量是 B种足球数量的2 倍,B 种足球单价比 A种足球单价多80 元/个.
(1)求A,B两种足球的单价;
(2)由于该校今年被定为“足球特色校”,学校决定再次购买 A,B两种足球共 18个,且本次购买 B 种足球的数量不少于A 种足球数量的2倍,若单价不变,则本次如何购买才能使费用W 最少
4. 如图,lAlB分别表示 A 步行与 B 骑车在同一路上行驶的路程s与时间t的关系.
(1)B出发时与A 相距 千米;
(2)走了一段路后,自行车发生故障进行修理,所用的时间是 小时;
(3)B出发后 小时与A 相遇;
(4)求出A行走的路程s与时间t的函数关系式;(写出计算过程)
(5)请通过计算说明:若B 的自行车不发生故障,保持出发时的速度前进,何时与 A 相遇
5.某校计划购买一批学习笔记本,已知1本甲种笔记本和3本乙种笔记本共需26元;3本甲种笔记本和2 本乙种笔记本共需29 元.
(1)求购买一本甲种笔记本和一本乙种笔记本各需多少元;
(2)学校计划购进这两种笔记本共70本,并且甲种笔记本的数量不超过乙种笔记本数量的2倍,若设学校计划购进甲种笔记本x本.
①填写下表:
甲种笔记本数量 10
乙种笔记本数量 30
所需总费用
②写出购买这两种笔记本所需要费用y(单位:元)关于x的函数关系式;请设计出最省钱的购买方案,并说明理由.
6.某文化用品商店出售书包和文具盒,书包每个定价40元,文具盒每个定价10 元,该店制定了两种优惠方案:方案一,买一个书包赠送一个文具盒;方案二:按总价的九折付款,购买时,顾客只能选用其中的一种方案.某学校为给学生发奖品,需购买 5 个书包,文具盒若干(不少于5个).设文具盒个数为x(单位:个),付款金额为y(单位:元).
(1)分别写出两种优惠方案中y与x之间的关系式.
方案一:
方案二:
(2)若购买20 个文具盒,通过计算比较以上两种方案中哪种更省钱;
(3)学校计划用540元钱购买这两种奖品,最多可以买到 个文具盒(直接回答即可).
第6 课时 一次函数与方程、不等式
1.如图,一次函数y=-x+4的图象分别与x轴,y轴交于A,B 两点,动点P 从点B 出发,沿BA运动到点A,且不与点A,B重合,过点P分别作x轴,y轴的垂线,垂足分别为 C,D,则四边形OCPD的周长 ( )
A.先减小后增大 B.先增大后减小
C.不变 D.逐渐增大
2.已知直线y=2x+4与x轴交于点A,与y轴交于点 B,则△AOB的面积为 ( )
A.8 B.6 C.4 D.2
3.如图,已知函数y=-2x+4,观察图象回答下列问题:
(1)x 时,y>0;(2)x 时,y<0;
(3)x 时,y=0;(4)x 时,y>4.
4.如图是y=kx+b的图象,则b= ,与x轴的交点坐标为 ,y 随x的增大而
5.直线 与 的图象如图所示,则:
(1)当x 时,y =y ;
(2)当x 时,y(3)当x l时,y >y .
6.画出函数y=2x+4 的图象,并利用图象直接回答当x为何值时:
(1)y=0;
(2)y>2.
7.在平面直角坐标系中,点 A,B的坐标分别是(m,3),(3m --1,3). 若线段 AB 与直线y=2x+1 相交,求 m的取值范围.
8.如图,在平面直角坐标系xOy中,一次函数的图象经过点A(2,3)与点B(0,5).
(1)求此一次函数的表达式;
(2)若点 P 为此一次函数图象上一点,且△POB的面积为10,求点 P 的坐标.
9.如图,已知直线AB 的函数解析式为y=2x+10,与y轴交于点 A,与x轴交于点 B.
(1)直接写出 A 点的坐标 ,B 点的坐标 ;
(2)若点 P(a,b)为线段AB上的一个动点,作PE⊥y轴于点 E,PF⊥x 轴于点 F,连接EF,问:
①若△PBO的面积为S,求 S关于a的函数关系式;
②直接写出 EF 的最小值 .
第十九章 一次函数
19.1 函数
第 1 课时 变量与函数
1. D 2. D 3.①②③
4. y=2x+4 5. T=20-2t
6.解:(1)常量是8,变量是 v,s.
(2)常量是 45,2,变量是s,t.
(3)常量是 100,变量是 v,t.
7.解:(1)当x=2时,
y=(x+1)(x--2)=(2+1)(2-2)=0,
当x=-3时,
y=(x+1)(x-2)=(-3+1)(-3-2)=10.
(2)当x=2时,
当x=-3时,
8.解:(1)梯形面积y 与上底长 x 之间的关系式y=4x+60.
(2)用表格表示当x 从 10 变到 15 时(每次增加 1),y的相应值
x 10 11 12 13 14 15 16
y 100 104 108 112 116 120 124
(3)当x每增加1时,y增加4.
(4)当x=0时,y等于60,此时它表示的是三角形.
9.解:(1)Q=800-50t.
(2)当t=6时,
答:6 h后,池中还有500 m 水.
(3)当Q=200 m 时,800-50t=200.
解得t=12.
答:12h后,池中还有200m 的水.
第2课时 函数的图象
1. C 2. C
3.这一天的最高气温约是26℃(答案不唯一)
4.(1)10 (2)1.7 5.大于 4
6.解:(1)12
(2)x每增加1千克,y增加0.5cm.
(3)y=0.5x+12,0≤x≤25.
7.解:(1)10
(2)当x>2时,每千米的单价为(14-10)÷(4-2)=2.∴当x>2时,y=10+2(x-2)=2x+6.
(3)当x=18时,y=2×18+6=42元.
答:这位乘客需付出租车车费42 元.
8.解:(1)甲 10 乙 5
(2)10(3)根据图象用路程除以时间即得:甲的速度为6÷30=0.2千米/分,乙的速度为 千米/分.
9.解:画图,如图.
(1)由图象可知当-1(2)由图象可知当019.2 一次函数
第 1 课时正比例函数
1. A 2. B 3. B 4.-1 5.120≤y≤180
6.解:(1)y=-4x是正比例函数,比例系数是-4.(2)y=3x-1 不是正比例函数.
是正比例函数,比例系数是 .
不是正比例函数.
(5)y=-0.9x是正比例函数,比例系数是-0.9.
是正比例函数,比例系数是(
7.解:(1)根据题意,得k+3≠0,解得k≠-3.
(2)根据题意,得k+3>0,解得k>-3.
(3)根据题意,得k+3<0,解得k<-3.
(4)把(1,1)代入 y=(k+3)x得k+3=1,解得k=-2,
即k为-2时,函数图象经过点(1,1).
8.解:(1)如图.
(2)两条直线的交角为 90度.
猜想:当两个一次函数两系数之积为-1时,两条直线的交角为90度,即垂直.
9.解:∵正比例函数 的图象 y随x 的增大而减小,
且m--1<0.
∴m=7 或-1且m<1.∴m=-1.
∴当m为-1时,正比例函数 的图象在第二、四象限 y随x 的增大而减小.
第2 课时 一次函数的概念
1. B 2. m≠1 2 3.±1 4. m≠2,n=2
5. y=-6x+20 是
6.(1)v=2t, 是一次函数. (2)5米/秒
7.解:(1)由题意可得|k|=1,k-1≠0.
解得 k=-1.
(2)当x=3时,y=-2x-3=-9.
(3)当y=0时,0=-2x-3.
解得
8.解:(1)根据题意可得y=70x,是一次函数.
(2)根据题意可得 y=0.53x,是一次函数.
(3)根据题意可得 y=4+40x,是一次函数.
(4)根据题意可得 y=1.5(x-20),是一次函数.
9.解:(1)∵y+a与x-b成正比例,
设比例系数为k,则y+a=k(x--b).
整理,得y=kx-kb-a.
∴y是x的一次函数.
(2)把x=-1时,y=-15;x=7时,y=1.
分别代入y=kx-kb-a,得
解得
则该一次函数为y=2x-13.
第 3 课时 一次函数的图象与性质
1. D 2. D 4.(3) 5. y=-3x+2
6.解:(1)图略.
(2)减小 (3)x=2 (4)x>4
7.(1)m>-2
(2)n>3 (3)m≠-2,n=3
8.(1)k=-3 (2)k=± (3)k=4 (4)k>3
9.解:(1)当x=0时,y=4;当y=0时,x=-2,图略.
x<-2.
第 4 课时 求一次函数的解析式
1. C 2. B 3. y=2x+2 4.3 5. y=-x+10
6.解:(1)把A(1,1)和点 B(--3,5)代入 y=kx+b,得 解得
∴直线AB所对应的函数解析式为y=-x+2.
(2)把x=4代入y=-x+2,得y=-4+2=-2.
∴点(4,-2)在直线 AB 上.
7.解:(1)设y+2=k(x--3),
把x=5,y=2代入,得2+2=k(5-3).
解得k=2.则y+2=2(x-3).
即y与x之间的函数解析式为y=2x--8.
(2)把y=4代入y=2x-8,得2x-8=4.解得x=6.
8.解:(1)4
(2)设直线 CD的函数解析式为y=kx+c,将C(3,4),D(-4,3)代入,得 解得 故直线 CD的函数解析式为
(3)点(-5,-4)不在直线CD上,理由如下:
∵当x=-5时,
∴点(-5,-4)不在直线 CD 上.
9.解:(1)∵直线
∴当x=0时,y=2;
当y=0时,x=-4.
∵直线 交x轴于点A,交 y轴于点B,
∴点 A 的坐标为(-4,0),点 B 的坐标为(0,2).
(2)由(1)知,点A 的坐标为(-4,0),点 B的坐标为(0,2),
∴OA=4,OB=2.
设点 C的坐标为(m,n)
得n=1.
∵点C在线段AB 上, 得m=-2.
∴点C的坐标为(-2,1).
设直线OC的解析式为y=kx,
-2k=1,得
∴直线OC 的函数解析式为
第5课时 一次函数的应用
1.解:(1)20 60÷(12-9)=20(米/分).
(2)(60-40)÷20=1(分钟),
∴点C的坐标为(5+1,60),即(6,60).
设线段BC的表达式y=kx+b(k≠0),
将 B(5,40),C(6,60) 两点 代 入 y = kx+b,得
解得
∴线段BC的表达式为y=20x-60(5≤x≤6).
(3)4 设线段DE的表达式为y=mx+n(m≠0),将 D(9,60), E(12,0) 代入 y = mx+ n,得 解得
∴线段DE的表达式为y=-20x+240(9≤x≤12).
当y=50时,有20x-60=50或-20x+240=50,解得 或
(分钟).
2.解:(1)由图象知,520+12a-2×10a=424,∴a=12.
(2)设当12≤x≤20时,y与x之间的函数关系式为y=kx+b,由题意,得 解得 y=-53x+1 060,当x=16时,y=212,
即排队到第16分钟时,食堂排队等候打饭菜的学生有212 人.
(3)设需同时开放 n个打饭窗口,则由题意,知10n×8≥520+12×8.
解得 n≥7.7.
∵n为整数,∴n最小=8.
答:至少需要同时开放8个打饭窗口.
3.解:(1)设A 种足球单价为x 元/个,则 B 足球单价为(x+80)元/个,
根据题意,得
解得x=120.
经检验,x=120是方程的解.
答:A 种足球单价为 120 元/个,B 足球单价为 200元/个.
(2)设再次购买A种足球x个,则B种足球为(18-x)个.根据题意,得 W=120x+200(18-x)=-80x+3 600.
∵18-x≥2x,∴x≤6.
∵--80<0,∴W随x的增大而减小.
∴当x=6时,W最小,此时18-x=12.
答:本次购买 A 种足球6个,B种足球12个,才能使购买费用W 最少.
4.解:(1)10 (2)1 (3)3
(4)根据函数图象可知直线 lA 经过点(0,10),(3,25).
设直线l 的解析式为s=kt+b,则
解得k=5,b=10.
∴s=5t+10.
(5)设直线 lB 的解析式为s=kt,
∵点(0.5,7.5)在直线lB 上,
∴7.5=k×0.5.得k=15.
∴s=15t.∴{S=5t+10,
解得 s=15,t=1.
故若 B的自行车不发生故障,保持出发时的速度前进,出发后 1小时与 A 相遇.
5.解:(1)设购买一本甲种笔记本和一本乙种笔记本分别需要x元、y元,
得
答:购买一本甲种笔记本和一本乙种笔记本分别需要5元、7元.
(2)①40 60 470 410
由题意可得,当购买甲种笔记本数量为10本时,则购买的乙种笔记本数量是60本,所需的总费用为 10×5+60×7=50+420=470(元),当购买乙种笔记本数量为 30本时,则购买的甲种笔记本数量是 40本,所需的总费用为40×5+30×7=200+210=410(元).
②由题意可得,y=5x+7(70--x)=5x+490--7x=-2x+490.
∵甲种笔记本的数量不超过乙种笔记本数量的2倍,∴x≤2(70-x).
解得
∴当x=46时,y取得最小值,此时y=-2×46+490=398,70-x=24.
答:购买这两种笔记本所需要费用y(单位:元)关于x的函数关系式是y=-2x+490,最省钱的购买方案是购买甲种笔记本46 本,乙种笔记本24本.
6.解:(1)10x+150 9x+180
由题意,可得
y =40×5+10(x-5)=10x+150,
y =(40×5+10x)×0.9=9x+180.
(2)当x=20时,
y =10×20+150=350,
y =9×20+180=360.
可看出方案一省钱.
(3)40
第6 课时 一次函数与方程、不等式
1. C 2. C 3.(1)<2 (2)>2 (3)=2 (4)<0
4.-2 ( , ) 增大
5.(1)=1 (2)>1 (3)<1
6.解:当x=0时,y=4;当y=0时,x=-2,
即该直线经过点(0,4),(-2,0)两点,其图象如图所示.
(1)根据图象知,当x=--2时,y=0.
(2)根据图象知,当x>--1时,y>2.
7.解:当y=3时,2x+1=3,解得x=1.所以直线 y=3 与直线y=2x+1的交点为(1,3).
当点 B 在点A 的右侧,则m≤1≤3m—1,解得 ≤1.
当点 B 在点A 的左侧,则3m-1≤1≤m,无解,所以m的取值范围为
8.解:(1)设一次函数的表达式为y=kx+b,把点 A(2,3)
和点 B(0,5)代入,得 解得
此一次函数的表达式为y=-x+5.
(2)设点 P 的坐标为(a,-a+5),
∵B(0,5),∴OB=5.
又∵△POB的面积为 10,
∴|a|=4.∴a=±4.
∴点 P 的坐标为(4,1)或(-4,9).
9.解:(1)A(0,10) B(-5,0)
对于直线AB的解析式y=2x+10,当x=0时,y=10;当y=0时,x=-5.
(2)连接OP,如图.
①∵P(a,b)在线段AB上,∴b=2a+10.
由0≤2a+10≤10,得到--5≤a≤0.
由(1),得 OB=5.
则 25(-5≤a≤0);
∵∠PFO=∠FOE=∠OEP=90°,
∴四边形 PFOE 为矩形.
∴EF=PO.
∵O为定点,P 在线段AB 上运动,
∴当OP⊥AB时,OP 取得最小值.
综上所述,存在点 P使得 EF的值最小,最小值为 2 .
19.1 函数
中小学教育资源及组卷应用平台
第1 课时 变量与函数
1.函数 中,自变量x的取值范围是( )
A.x≤-5 B. x≠-5
C. x> -5 D.x≥-5
2.某居民小区收取电费的标准是0.6 元/千瓦时,当用电量为x(单位:千瓦时)时,收取电费为y(单位:元).在这个问题中,下列说法中正确的是 ( )
A.x是自变量,0.6元/千瓦时是因变量
B.y是自变量,x是因变量
C.0.6 元/千瓦时是自变量,y是因变量
D.x是自变量,y是因变量
3.下列各式①y=0.5x-2;②y=|2x|;③3y+5=x; 中,y是x的函数的有 (只填序号).
4.某市出租车收费按里程计算,3 千米以内(含3千米)收费10 元,超过3千米,每增加1 千米加收2元,则当x≥3时,车费y(单位:元)与x(单位:千米)之间的关系式为 .
5.冷冻一个20℃的物体,若它每小时下降2℃,则物体的温度 T(单位:℃)与冷冻时间t(单位:时)的关系式是 .
6.设路程为s km,速度为v km/h,时间th,指出下列各式中的常量与变量.
7.当x=2及x=-3时,分别求出下列函数的函数值:
(1)y=(x+1)(x-2);
8.如图,梯形上底的长是x,下底的长是15,高是8.
(1)梯形面积y与上底长x之间的关系式是什么
(2)用表格表示当x从10变到16时(每次增加1),y的相应值;
x 10 11 12 13 14 15 16
y
(3)当x每增加1时,y如何变化
(4)当x=0时,y等于什么 此时它表示的是什么
9.已知水池中有800 m 的水,每小时抽出50 m .
(1)写出剩余水的体积Q(单位:m )与时间t(单位:h)之间的函数关系式;
(2)6 h后池中还有多少水
(3)多少小时后,池中还有200 m 的水
第2 课时 i函数的图象
1.下面说法中正确的是 ( )
A.两个变量间的关系只能用关系式表示
B.图象不能直观的表示两个变量间的数量关系
C.借助表格可以表示出因变量随自变量的变化情况
D.以上说法都不对
2.1-6 个月的婴儿生长发育得非常快,出生体重为4000克的婴儿,他们的体重y(单位:克)和月龄x(单位:月)之间的关系如下表,则6个月大的婴儿的体重为 ( )
月龄/月 1 2 3 4 5
体重/克 4 700 5 400 6 100 6800 7 500
A.7 600 克 B.7 800 克
C.8 200 克 D.8 500 克
3.如图是某地区某一天内的气温变化图,结合该图给出的信息写出一个正确的结论:
4.如图反映了某出租公司乘车费用y(单位:元)与路程x(单位:千米)之间的关系,请你根据图中信息回答下列问题:
(1)公司规定的起步价是 元;
(2)该公司规定除起步价外,超过5千米的每增加1千米多收 元.
5.如图,l 反映了某公司产品的销售收人与销售量的关系,l 反映了该公司产品的销售成本与销售量的关系,根据图象判断:当该公司赢利(收入大于成本)时,销售量必须 .
6.已知某弹簧长度的最大挂重为25 千克,在弹性限度内,用x表示物体的质量,用y表示弹簧的长度,其关系如下表:
所挂物体质量的质量/千克 0 1 2 3 4 5 6 7 8
弹簧的长度/cm 12 12.5 13 13.5 14 14.5 15 15.5 16
(1)弹簧不挂物体时的长度是 cm;
(2)随着x的变化,y的变化趋势是: ;
(3)根据表中数据的变化关系,写出y与x的关系式,并指出自变量的取值范围是 :
7.某出租车计费的方法如图所示,x(单位:km)表示行驶里程,y(单位:元)表示车费,请根据图象解答下列问题:
(1)该地出租车起步价是 元;
(2)当x>2时,求y与x之间的关系式;
(3)若某乘客一次乘出租车的里程为18 km,则这位乘客需付出租车车费多少元
8.甲骑自行车、乙骑摩托车沿相同路线由 A 地到B地,行驶过程中路程与时间的函数关系的图象如图.根据图象解决下列问题:
(1) 先出发,先出发 分钟; 先到达终点,先到 分钟.
(2)在什么时间段内,两人均行驶在途中(不包括起点和终点),在这一时间段内,请你根据下列情形填空:
当 时,甲在乙的前面时;
当 时,甲与乙相遇时;
当 时,甲在乙后面.
(3)分别求出甲、乙两人的行驶速度.
9.在如图所示的坐标系上,画出下列函数的图象:C 1(在图象的末端注明①②③);并根据图象在下列不同的定义域内,比较函数值的大小(用“ <”号连接):
(1)当-1
第 1 课时正比例函数
1.已知函数y=(a-1)x的图象过第一、三象限,那么a的取值范围是 ( )
A. a>1 B. a<1 C. a>0 D. a<0
2.在平面直角坐标系中,正比例函数 y =-3x的图象的大体位置是 ( )
3.已知函数y=(k-3)x,y随x的增大而减小,则常数 k的取值范围是 ( )
A. k>3 B. k<3
C. k<-3 D. k<0
4.已知函数 是正比例函数,则m= .
5.在函数 中,若自变量x的取值范围是50≤x≤75,则函数值 y 的取值范 围为
6.下列函数哪些是正比例函数 是正比例函数的指出比例系数.
(1)y=-4x;(2)y=3x-1;(3)y= x;(4)y= ;
7.已知函数y=(k+3)x.
(1)k为何值时,函数为正比例函数;
(2)k为何值时,函数的图象经过第一、三象限;
(3)k为何值时,y随x的增大而减小
(4)k为何值时,函数图象经过点(1,1)
8.(1)在同一平面直角坐标系内画出正比例函数 与 的图象;
(2)请你用量角器度量一下这两条直线的交角,你会发现什么 写出你的猜想.
当m 为何值时,正比例函数 的图象在哪几个象限y随x的增大而减小
第2课时 一次函数的概念
1.下列函数不是一次函数的是 ( )
C. y= -x+1
2.函数y=(m-1)x+2-m是一次函数,则m满足的条件是 ,若此函数是正比例函数,则 m= .
3.已知 是一次函数,则k= .
4.函数 是一次函数,m,n 应满足的条件是 .
5.一般地,海拔高度每上升1 km,温度下降6℃.某时刻测量某市地面温度为20℃.设高出地面xkm处的温度为y℃,则y与x的函数关系式为 ,y x的一次函数.(填“是”或“不是”)
6.一个小球由静止开始从一个斜坡向下滚动,其速度每秒增加2 米.
(1)求这个小球速度v随时间t变化的函数关系.它是一次函数吗
(2)求第2.5 秒时小球的速度.
7.已知 是一次函数.
(1)求k的值;
(2)求x=3时,y的值;
(3)当y=0时,x的值.
8.写出下列各题中x与y之间的解析式,并判断y是否是x的一次函数.
(1)在时速为70 千米的匀速运动中,路程y(单位:千米)与时间(单位:小时)的关系;
(2)居民用电标准是每千瓦时0.53 元,则电费y(单位:元)与用电量x(单位:千瓦时)之间的关系;
(3)汽车离开A站4千米,再以40千米/时的平均速度行驶了x小时,那么汽车离开 A站的距离y(单位:千米)与时间(单位:小时)之间的关系;
(4)某车站规定旅客可以免费携带不超过20千克的行李,超过部分每千克收取1.5 元的行李费用,则旅客需交的行李费y(单位:元)与携带行李重量x(单位:千克)之间的关系.
9.已知y+a与x-b成正比例(其中a,b都是常数).
(1)试说明y是x的一次函数;
(2)如果x=-1时,y=-15;x=7时,y=1,求这个一次函数的解析式.
第3课时 一次函数的图象与性质
1.一次函数y =kx+b的图象如图所示,则k,b的值为( )
A. k<0,b<0
B. k<0,b>0
C. k>0,b<0
D. k>0,b>0
2.关于函数y=-2x+1,下列结论正确的是( )
A.图象必经过点( -2,1)
B. y随x的增大而增大
C.图象经过第一、二、三象限
D.当 时,y<0
3.一次函数y=(2m-1)x+1,若y随x的增大而增大,则m的取值范围是 .
4.关于x的一次函数 的图象可能正确的是 .
5.把函数y=-3x的图象向上平移2 个单位长度所得图象的解析式是 .
6.已知函数y=-x+4,回答下列问题:
(1)请在下图的直角坐标系中画出函数y=-x+4的图象;
(2)y随x的增大而 ;
(3)当y=2时,x的值为 ;
(4)当y<0时,x的取值范围是 .
7.已知一次函数y=(2m+4)x+(3-n),求:
(1)当m为何值时,y随x的增大而增大;
(2)当n为何值时,函数图象与y轴的交点在x轴下方;
(3)m,n 为何值时,函数图象过原点.
8.已知一次函数
(1)k为何值时,它的图象经过原点;
(2)k为何值时,它的图象经过点(0,-2);
(3)k为何值时,它的图象平行于直线y=-x.
(4)若这个函数是一次函数,且y随x的增大而减小,求k的取值范围.
9.已知一次函数y=2x+4.
(1)在如图所示的平面直角坐标系中,画出函数的图象;
(2)求图象与坐标轴所围成图形的面积;
(3)利用图象直接写出:当y<0时,x的取值范围.
第4 课时 求一次函数的解析式
1.如图,直线 AB 对应的函数解析式是 ( )
2.若直线l与直线y=3x+1关于y轴对称,则直线l的解析式为( )
A. y= -3x-1 B. y= -3x+1
C. y=3x-1 D. y= -x+1
3.已知y与x+1 成正比例,比例系数是2,则y与x的函数关系式是 .
4.如果函数y=4x+3-k的图象经过原点,那么k= .
5.已知一次函数的图象与直线y=-x+1 平行,且过点(8,2),则此一次函数的解析式为
6.在平面直角坐标系中,直线y=kx+b经过点A(1,1)和点B( -3,5).
(1)求直线AB 所对应的函数解析式;
(2)判断点(4,-2)是否在直线AB 上.
7.已知:y+2 与x-3 成正比例,且当x=5时,y=2.
(1)求y与x之间的函数解析式;
(2)当y=4时,x的值是多少.
8.如图,在平面直角坐标系xOy中,已知点A(0,8),B(6,0),点C(3,a)在线段AB 上.
(1)则a的值为 ;
(2)若点 D( -4,3),求直线 CD 的函数解析式;
(3)点(-5,-4)在直线 CD 上吗 说明理由.
9.如图,已知直线 交x轴于点A,交y轴于点 B.
(1)求A,B两点的坐标;
(2)已知点 C 是线段 AB 上的一点,当S△AOC= 时,求直线OC 的解析式.
第5课时 一次函数的应用
1.某次大型活动,组委会启用无人机航拍活动过程,在操控无人机时应根据现场状况调节高度,已知无人机在上升和下降过程中速度相同,设无人机的飞行高度为y(单位:米),操控无人机的时间为x(单位:分),y与x之间的函数图象如图所示.
(1)无人机的速度为 米/分;
(2)求线段BC 所表示的y与x之间函数表达式;
(3)无人机在 50 米上空持续飞行时间为 分钟.
2.小越为湖州某校食堂王经理建议食堂就餐情况,经调查发现就餐时,有520 人排队吃饭就餐,就餐开始后仍有学生继续前来排队进食堂.设学生按固定的速度增加,食堂打饭窗口打饭菜的速度也是固定的.若每分钟该食堂新增排队学生数12 人,每个打饭窗口每分钟打饭菜10 人.已知食堂的前a 分钟只开放了两个打饭窗口;某一天食堂排队等候的学生数y(单位:人)与打饭菜时间x(单位:分钟)的关系如图所示.
(1)求a的值;
(2)求排队到第16 分钟时,食堂排队等候打饭菜的学生人数;
(3)若要在开始打饭菜后8 分钟内让所有排队的学生都能进食堂后来到食堂窗口的学生随到随吃,那么小赵应该建议食堂王经理一开始就需要至少同时开放几个打饭窗口
3.某校去年购买了A,B 两种足球,费用分别为2 400 元和2 000 元,其中A 种足球数量是 B种足球数量的2 倍,B 种足球单价比 A种足球单价多80 元/个.
(1)求A,B两种足球的单价;
(2)由于该校今年被定为“足球特色校”,学校决定再次购买 A,B两种足球共 18个,且本次购买 B 种足球的数量不少于A 种足球数量的2倍,若单价不变,则本次如何购买才能使费用W 最少
4. 如图,lAlB分别表示 A 步行与 B 骑车在同一路上行驶的路程s与时间t的关系.
(1)B出发时与A 相距 千米;
(2)走了一段路后,自行车发生故障进行修理,所用的时间是 小时;
(3)B出发后 小时与A 相遇;
(4)求出A行走的路程s与时间t的函数关系式;(写出计算过程)
(5)请通过计算说明:若B 的自行车不发生故障,保持出发时的速度前进,何时与 A 相遇
5.某校计划购买一批学习笔记本,已知1本甲种笔记本和3本乙种笔记本共需26元;3本甲种笔记本和2 本乙种笔记本共需29 元.
(1)求购买一本甲种笔记本和一本乙种笔记本各需多少元;
(2)学校计划购进这两种笔记本共70本,并且甲种笔记本的数量不超过乙种笔记本数量的2倍,若设学校计划购进甲种笔记本x本.
①填写下表:
甲种笔记本数量 10
乙种笔记本数量 30
所需总费用
②写出购买这两种笔记本所需要费用y(单位:元)关于x的函数关系式;请设计出最省钱的购买方案,并说明理由.
6.某文化用品商店出售书包和文具盒,书包每个定价40元,文具盒每个定价10 元,该店制定了两种优惠方案:方案一,买一个书包赠送一个文具盒;方案二:按总价的九折付款,购买时,顾客只能选用其中的一种方案.某学校为给学生发奖品,需购买 5 个书包,文具盒若干(不少于5个).设文具盒个数为x(单位:个),付款金额为y(单位:元).
(1)分别写出两种优惠方案中y与x之间的关系式.
方案一:
方案二:
(2)若购买20 个文具盒,通过计算比较以上两种方案中哪种更省钱;
(3)学校计划用540元钱购买这两种奖品,最多可以买到 个文具盒(直接回答即可).
第6 课时 一次函数与方程、不等式
1.如图,一次函数y=-x+4的图象分别与x轴,y轴交于A,B 两点,动点P 从点B 出发,沿BA运动到点A,且不与点A,B重合,过点P分别作x轴,y轴的垂线,垂足分别为 C,D,则四边形OCPD的周长 ( )
A.先减小后增大 B.先增大后减小
C.不变 D.逐渐增大
2.已知直线y=2x+4与x轴交于点A,与y轴交于点 B,则△AOB的面积为 ( )
A.8 B.6 C.4 D.2
3.如图,已知函数y=-2x+4,观察图象回答下列问题:
(1)x 时,y>0;(2)x 时,y<0;
(3)x 时,y=0;(4)x 时,y>4.
4.如图是y=kx+b的图象,则b= ,与x轴的交点坐标为 ,y 随x的增大而
5.直线 与 的图象如图所示,则:
(1)当x 时,y =y ;
(2)当x 时,y
6.画出函数y=2x+4 的图象,并利用图象直接回答当x为何值时:
(1)y=0;
(2)y>2.
7.在平面直角坐标系中,点 A,B的坐标分别是(m,3),(3m --1,3). 若线段 AB 与直线y=2x+1 相交,求 m的取值范围.
8.如图,在平面直角坐标系xOy中,一次函数的图象经过点A(2,3)与点B(0,5).
(1)求此一次函数的表达式;
(2)若点 P 为此一次函数图象上一点,且△POB的面积为10,求点 P 的坐标.
9.如图,已知直线AB 的函数解析式为y=2x+10,与y轴交于点 A,与x轴交于点 B.
(1)直接写出 A 点的坐标 ,B 点的坐标 ;
(2)若点 P(a,b)为线段AB上的一个动点,作PE⊥y轴于点 E,PF⊥x 轴于点 F,连接EF,问:
①若△PBO的面积为S,求 S关于a的函数关系式;
②直接写出 EF 的最小值 .
第十九章 一次函数
19.1 函数
第 1 课时 变量与函数
1. D 2. D 3.①②③
4. y=2x+4 5. T=20-2t
6.解:(1)常量是8,变量是 v,s.
(2)常量是 45,2,变量是s,t.
(3)常量是 100,变量是 v,t.
7.解:(1)当x=2时,
y=(x+1)(x--2)=(2+1)(2-2)=0,
当x=-3时,
y=(x+1)(x-2)=(-3+1)(-3-2)=10.
(2)当x=2时,
当x=-3时,
8.解:(1)梯形面积y 与上底长 x 之间的关系式y=4x+60.
(2)用表格表示当x 从 10 变到 15 时(每次增加 1),y的相应值
x 10 11 12 13 14 15 16
y 100 104 108 112 116 120 124
(3)当x每增加1时,y增加4.
(4)当x=0时,y等于60,此时它表示的是三角形.
9.解:(1)Q=800-50t.
(2)当t=6时,
答:6 h后,池中还有500 m 水.
(3)当Q=200 m 时,800-50t=200.
解得t=12.
答:12h后,池中还有200m 的水.
第2课时 函数的图象
1. C 2. C
3.这一天的最高气温约是26℃(答案不唯一)
4.(1)10 (2)1.7 5.大于 4
6.解:(1)12
(2)x每增加1千克,y增加0.5cm.
(3)y=0.5x+12,0≤x≤25.
7.解:(1)10
(2)当x>2时,每千米的单价为(14-10)÷(4-2)=2.∴当x>2时,y=10+2(x-2)=2x+6.
(3)当x=18时,y=2×18+6=42元.
答:这位乘客需付出租车车费42 元.
8.解:(1)甲 10 乙 5
(2)10
9.解:画图,如图.
(1)由图象可知当-1
第 1 课时正比例函数
1. A 2. B 3. B 4.-1 5.120≤y≤180
6.解:(1)y=-4x是正比例函数,比例系数是-4.(2)y=3x-1 不是正比例函数.
是正比例函数,比例系数是 .
不是正比例函数.
(5)y=-0.9x是正比例函数,比例系数是-0.9.
是正比例函数,比例系数是(
7.解:(1)根据题意,得k+3≠0,解得k≠-3.
(2)根据题意,得k+3>0,解得k>-3.
(3)根据题意,得k+3<0,解得k<-3.
(4)把(1,1)代入 y=(k+3)x得k+3=1,解得k=-2,
即k为-2时,函数图象经过点(1,1).
8.解:(1)如图.
(2)两条直线的交角为 90度.
猜想:当两个一次函数两系数之积为-1时,两条直线的交角为90度,即垂直.
9.解:∵正比例函数 的图象 y随x 的增大而减小,
且m--1<0.
∴m=7 或-1且m<1.∴m=-1.
∴当m为-1时,正比例函数 的图象在第二、四象限 y随x 的增大而减小.
第2 课时 一次函数的概念
1. B 2. m≠1 2 3.±1 4. m≠2,n=2
5. y=-6x+20 是
6.(1)v=2t, 是一次函数. (2)5米/秒
7.解:(1)由题意可得|k|=1,k-1≠0.
解得 k=-1.
(2)当x=3时,y=-2x-3=-9.
(3)当y=0时,0=-2x-3.
解得
8.解:(1)根据题意可得y=70x,是一次函数.
(2)根据题意可得 y=0.53x,是一次函数.
(3)根据题意可得 y=4+40x,是一次函数.
(4)根据题意可得 y=1.5(x-20),是一次函数.
9.解:(1)∵y+a与x-b成正比例,
设比例系数为k,则y+a=k(x--b).
整理,得y=kx-kb-a.
∴y是x的一次函数.
(2)把x=-1时,y=-15;x=7时,y=1.
分别代入y=kx-kb-a,得
解得
则该一次函数为y=2x-13.
第 3 课时 一次函数的图象与性质
1. D 2. D 4.(3) 5. y=-3x+2
6.解:(1)图略.
(2)减小 (3)x=2 (4)x>4
7.(1)m>-2
(2)n>3 (3)m≠-2,n=3
8.(1)k=-3 (2)k=± (3)k=4 (4)k>3
9.解:(1)当x=0时,y=4;当y=0时,x=-2,图略.
x<-2.
第 4 课时 求一次函数的解析式
1. C 2. B 3. y=2x+2 4.3 5. y=-x+10
6.解:(1)把A(1,1)和点 B(--3,5)代入 y=kx+b,得 解得
∴直线AB所对应的函数解析式为y=-x+2.
(2)把x=4代入y=-x+2,得y=-4+2=-2.
∴点(4,-2)在直线 AB 上.
7.解:(1)设y+2=k(x--3),
把x=5,y=2代入,得2+2=k(5-3).
解得k=2.则y+2=2(x-3).
即y与x之间的函数解析式为y=2x--8.
(2)把y=4代入y=2x-8,得2x-8=4.解得x=6.
8.解:(1)4
(2)设直线 CD的函数解析式为y=kx+c,将C(3,4),D(-4,3)代入,得 解得 故直线 CD的函数解析式为
(3)点(-5,-4)不在直线CD上,理由如下:
∵当x=-5时,
∴点(-5,-4)不在直线 CD 上.
9.解:(1)∵直线
∴当x=0时,y=2;
当y=0时,x=-4.
∵直线 交x轴于点A,交 y轴于点B,
∴点 A 的坐标为(-4,0),点 B 的坐标为(0,2).
(2)由(1)知,点A 的坐标为(-4,0),点 B的坐标为(0,2),
∴OA=4,OB=2.
设点 C的坐标为(m,n)
得n=1.
∵点C在线段AB 上, 得m=-2.
∴点C的坐标为(-2,1).
设直线OC的解析式为y=kx,
-2k=1,得
∴直线OC 的函数解析式为
第5课时 一次函数的应用
1.解:(1)20 60÷(12-9)=20(米/分).
(2)(60-40)÷20=1(分钟),
∴点C的坐标为(5+1,60),即(6,60).
设线段BC的表达式y=kx+b(k≠0),
将 B(5,40),C(6,60) 两点 代 入 y = kx+b,得
解得
∴线段BC的表达式为y=20x-60(5≤x≤6).
(3)4 设线段DE的表达式为y=mx+n(m≠0),将 D(9,60), E(12,0) 代入 y = mx+ n,得 解得
∴线段DE的表达式为y=-20x+240(9≤x≤12).
当y=50时,有20x-60=50或-20x+240=50,解得 或
(分钟).
2.解:(1)由图象知,520+12a-2×10a=424,∴a=12.
(2)设当12≤x≤20时,y与x之间的函数关系式为y=kx+b,由题意,得 解得 y=-53x+1 060,当x=16时,y=212,
即排队到第16分钟时,食堂排队等候打饭菜的学生有212 人.
(3)设需同时开放 n个打饭窗口,则由题意,知10n×8≥520+12×8.
解得 n≥7.7.
∵n为整数,∴n最小=8.
答:至少需要同时开放8个打饭窗口.
3.解:(1)设A 种足球单价为x 元/个,则 B 足球单价为(x+80)元/个,
根据题意,得
解得x=120.
经检验,x=120是方程的解.
答:A 种足球单价为 120 元/个,B 足球单价为 200元/个.
(2)设再次购买A种足球x个,则B种足球为(18-x)个.根据题意,得 W=120x+200(18-x)=-80x+3 600.
∵18-x≥2x,∴x≤6.
∵--80<0,∴W随x的增大而减小.
∴当x=6时,W最小,此时18-x=12.
答:本次购买 A 种足球6个,B种足球12个,才能使购买费用W 最少.
4.解:(1)10 (2)1 (3)3
(4)根据函数图象可知直线 lA 经过点(0,10),(3,25).
设直线l 的解析式为s=kt+b,则
解得k=5,b=10.
∴s=5t+10.
(5)设直线 lB 的解析式为s=kt,
∵点(0.5,7.5)在直线lB 上,
∴7.5=k×0.5.得k=15.
∴s=15t.∴{S=5t+10,
解得 s=15,t=1.
故若 B的自行车不发生故障,保持出发时的速度前进,出发后 1小时与 A 相遇.
5.解:(1)设购买一本甲种笔记本和一本乙种笔记本分别需要x元、y元,
得
答:购买一本甲种笔记本和一本乙种笔记本分别需要5元、7元.
(2)①40 60 470 410
由题意可得,当购买甲种笔记本数量为10本时,则购买的乙种笔记本数量是60本,所需的总费用为 10×5+60×7=50+420=470(元),当购买乙种笔记本数量为 30本时,则购买的甲种笔记本数量是 40本,所需的总费用为40×5+30×7=200+210=410(元).
②由题意可得,y=5x+7(70--x)=5x+490--7x=-2x+490.
∵甲种笔记本的数量不超过乙种笔记本数量的2倍,∴x≤2(70-x).
解得
∴当x=46时,y取得最小值,此时y=-2×46+490=398,70-x=24.
答:购买这两种笔记本所需要费用y(单位:元)关于x的函数关系式是y=-2x+490,最省钱的购买方案是购买甲种笔记本46 本,乙种笔记本24本.
6.解:(1)10x+150 9x+180
由题意,可得
y =40×5+10(x-5)=10x+150,
y =(40×5+10x)×0.9=9x+180.
(2)当x=20时,
y =10×20+150=350,
y =9×20+180=360.
可看出方案一省钱.
(3)40
第6 课时 一次函数与方程、不等式
1. C 2. C 3.(1)<2 (2)>2 (3)=2 (4)<0
4.-2 ( , ) 增大
5.(1)=1 (2)>1 (3)<1
6.解:当x=0时,y=4;当y=0时,x=-2,
即该直线经过点(0,4),(-2,0)两点,其图象如图所示.
(1)根据图象知,当x=--2时,y=0.
(2)根据图象知,当x>--1时,y>2.
7.解:当y=3时,2x+1=3,解得x=1.所以直线 y=3 与直线y=2x+1的交点为(1,3).
当点 B 在点A 的右侧,则m≤1≤3m—1,解得 ≤1.
当点 B 在点A 的左侧,则3m-1≤1≤m,无解,所以m的取值范围为
8.解:(1)设一次函数的表达式为y=kx+b,把点 A(2,3)
和点 B(0,5)代入,得 解得
此一次函数的表达式为y=-x+5.
(2)设点 P 的坐标为(a,-a+5),
∵B(0,5),∴OB=5.
又∵△POB的面积为 10,
∴|a|=4.∴a=±4.
∴点 P 的坐标为(4,1)或(-4,9).
9.解:(1)A(0,10) B(-5,0)
对于直线AB的解析式y=2x+10,当x=0时,y=10;当y=0时,x=-5.
(2)连接OP,如图.
①∵P(a,b)在线段AB上,∴b=2a+10.
由0≤2a+10≤10,得到--5≤a≤0.
由(1),得 OB=5.
则 25(-5≤a≤0);
∵∠PFO=∠FOE=∠OEP=90°,
∴四边形 PFOE 为矩形.
∴EF=PO.
∵O为定点,P 在线段AB 上运动,
∴当OP⊥AB时,OP 取得最小值.
综上所述,存在点 P使得 EF的值最小,最小值为 2 .
