第十七章 勾股定理课时强化训练 2023—2024学年人教版数学八年级下册(含答案)
文档属性
| 名称 | 第十七章 勾股定理课时强化训练 2023—2024学年人教版数学八年级下册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 763.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-03 20:15:39 | ||
图片预览




文档简介
第十七章 勾股定理
17.1 勾股定理
中小学教育资源及组卷应用平台
第1 课时 勾股定理(一)——证明、简单计算
1.直角三角形两条直角边的长分别为3 和4,则斜边长为 ( )
A.4 B.5 C.6 D.10
2.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若( =21,大正方形的面积为13,则小正方形的边长为 ( )
A.
B.2
C.
D.
3.已知直角三角形的三边分别为6,8,x,则x=
4.直角三角形两条直角边的长分别为5,12,则斜边长为 ,斜边上的高为 .
5.如图,是由四个直角边分别为3和4 且全等的直角三角形拼成的“赵爽弦图”,那么阴影部分面积为 .
6.如图,求下列图形中未知正方形的面积或未知边的长度:
7.一个直角三角形一条边为7,另一条边为13,求第三边的长.
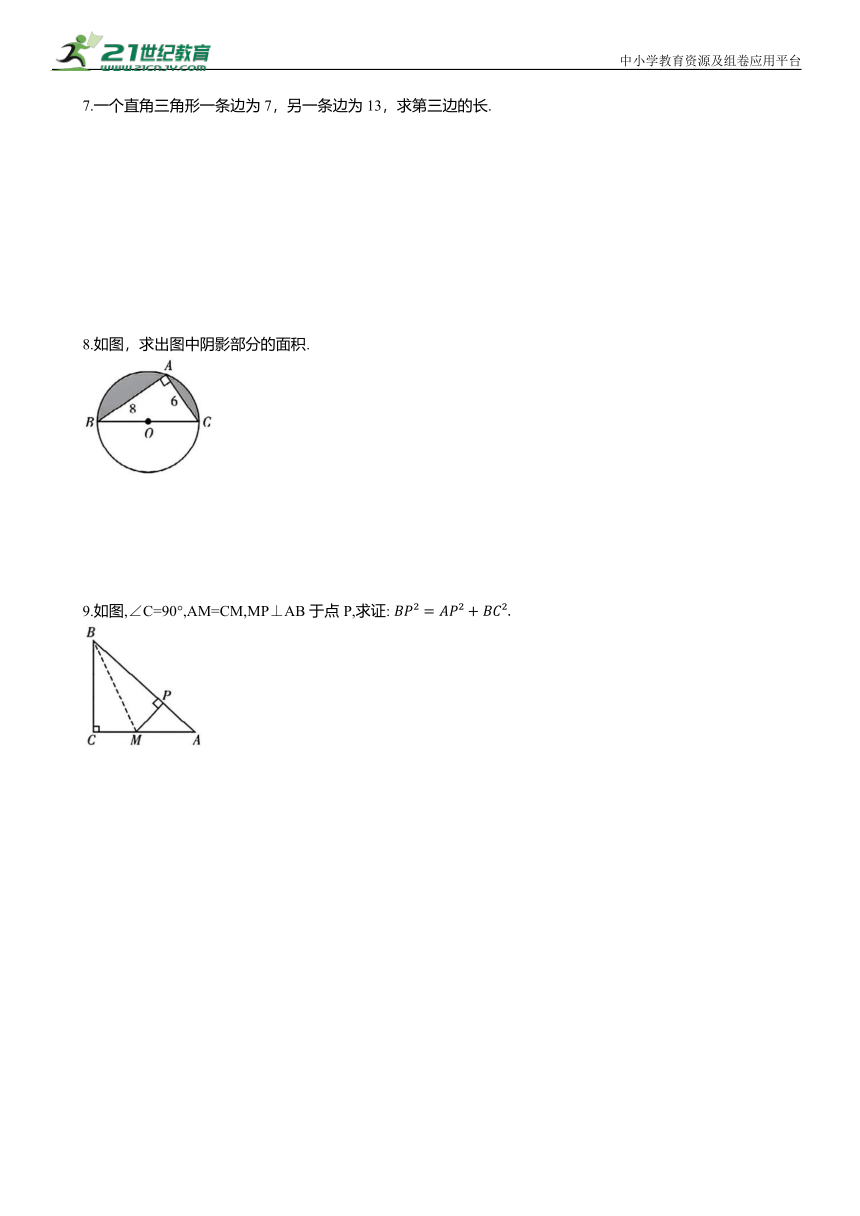
8.如图,求出图中阴影部分的面积.
9.如图,∠C=90°,AM=CM,MP⊥AB 于点 P,求证:
第2 课时 勾股定理(二)——实际应用
1.如图,图中的小正方形的边长为1,△ABC的三个顶点都在小正方形的顶点上,则△ABC的周长为 ( )
B.16
2. 如图,在Rt△ABC中,∠C =90°,将其绕B 点顺时针旋转一周,则分别以 BA,BC 为半径的圆形形成一圆环(阴影部分),为求该圆环的面积,只需测量一条线段的长度,这条线段就是( )
A. AD B. AB C. BD D. AC
3.如图,数轴上的点A表示的数是-1,点 B 表示的数是1,CB⊥AB于点B,且BC=2,以点 A 为圆心,AC 为半径画弧交数轴于点 D,则点 D 表示的数为 ( )
B.2
C.2.8
4.一个直角三角形的两条直角边分别是8cm ,15cm,斜边是17 cm,把直角边扩大到原来的2倍,那么斜边扩大到 cm.
5.如图是由4 个边长为1 的正方形构成的田字格,连接正方形的顶点在这个田字格中最多可以作出 条长度为 的线段.
6.如图,为修通铁路凿通隧道 AC,量出∠A =40°,∠B=50°,AB=5千米,BC=4千米,若每天凿隧道0.3 千米,问几天才能把隧道 AC 凿通
7.如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB 于点E,若AC=6,BC=8,CD =3.
(1)求 DE 的长;
(2)求△BDE 的面积.
8.已知:如图,△ABC的面积为84,BC=21,现将△ABC沿直线BC向右平移a(0(1)求 BC 边上的高;
(2)若 AB =10,
①求线段 DF 的长;
②连接AE,当△ABE 是等腰三角形时,求 a 的值.
9.细心观察图形,认真分析各式,然后回答问题:
(1)推算出OA 的长和S 的值;
(2)用含n(n为正整数)的式子表示上述规律;
(3)求 的值.
OA =1, OA =() +1=2, OA =() +1=3, OA =() +1=4, …… s = , S = , S = , ……
17.2 勾股定理的逆定理
第1 课时 勾股定理的逆定理(一)——计算、判别
1.下列命题中,假命题的是 ( )
A.在△ABC 中,若∠B +∠C = ∠A,则△ABC是直角三角形
B.在△ABC 中,若 则△ABC 是直角三角形
C.在△ABC中,若∠A: ∠B: ∠C =6: 8:10,则△ABC 是直角三角形
D.在△ABC 中,若 a: b: c =5: 4: 3,则△ABC 是直角三角形
2.已知△ABC,AB =5,BC =12,AC =13,点 P 是AC 上一个动点,则线段 BP 长的最小值是( )
B.5 C. D.12
3.定理“同位角相等,两直线平行”的逆定理是
4.△ABC的三边长分别是a,b,c,下列条件:①∠A=∠B--∠C;②∠A: ∠B: ∠C=3:4: 5;③a: b: c=5: 12: 13;④a =(b+c)(b-c);⑤三边之长为3 ,4 ,5 ,其中能判断△ABC 是直角三角形的是 .
5.已知a,b,c是一组勾股数,其中c最大,且c=2n +2n+1,a=2n+1,则b= .(用含 n的代数式表示,其中n为正整数)
6.判断由线段a,b,c组成的三角形是不是直角三角形,并说明理由.
(2)a=13,b=14,c=15.
7.如图,在4×3的正方形网格中,每个小正方形的边长都是1.
(1)分别求出线段AB,CD的长度;
(2)在图中画线段EF,使得 以 AB,CD,EF三条线段长为边能否构成直角三角形 并说明理由.
8.如图,△ABC 和△ADE 都是等腰直角三角形,AB=AC,AD=AE,∠BAC=∠DAE=90°.
(1)求证:△ACE≌△ABD;
(2)若AC=2,EC=4,DC =2 求∠ACD的度,数.
9.如图,在△ABC 中,∠ACB=90°,CD⊥AB 于点D,∠A,∠B,∠C所对的边分别为a,b,c,斜边上的高为h.
(1)求证:
(2)判断:三边分别为h,a+b,c+h的三角形是否为直角三角形 请说明理由.
第2课时 勾股定理的逆定理(二)——应用
1.甲、乙两艘客轮同时离开港口,航行的速度都是40 m/min,甲客轮用15 min到达点 A,乙客轮用20 min到达点 B,若A,B两点的直线距离为1 000 m,甲客轮沿着北偏东30°的方向航行,则乙客轮的航行方向可能是 ( )
A.北偏西30° B.南偏西30°
C.南偏东60° D.南偏西60°
2.将直角三角形的各边都缩小或扩大同样的倍数后,得到的三角形 ( )
A.可能是锐角三角形
B.不可能是直角三角形
C.仍然是直角三角形
D.可能是钝角三角形
3.在△ABC中,若三条边的长度分别为9,12,15,则以两个这样的三角形所拼成的四边形的面积是 .
4.甲船以每小时16 海里的速度从港口A 出发向北偏东50°的方向航行,乙船以每小时12海里的速度同时从港口A 出发向南偏东方向航行,离开港口2 小时后两船相距40 海里,则乙船向南偏东 °方向航行.
5.如图,已知点A(-1,0)和点B(1,2),在y轴正半轴上确定点 P,使得△ABP 为直角三角形,则满足条件的点 P 的坐标为 .
6.如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3m,BC=4m,CD=12m,DA=13 m,∠B=90°.小区为美化环境,欲在空地上铺草坪,已知草坪每平方米30元,试问铺满这块空地共需花费多少元
7.在寻找马航MH370 航班过程中,两艘搜救舰艇接到消息,在海面上有疑似漂浮目标A,B.接到消息后,一艘舰艇以16海里/时的速度离开港口 O(如图)向北偏东40°方向航行,另一艘舰艇在同时以12 海里/时的速度向北偏西一定角度的航向行驶,已知它们离港口一个半小时后相距30 海里,问另一艘舰艇的航行方向是北偏西多少度
8.某校有两个课外小组的同学到校外去采集植物标本,已知第一组的速度为30 m/min,第二组的速度为40 m/min,且两组行走的路线为直线,半小时后,两组同学同时停下来,这时两组同学正好相距1 500 m.
(1)请你判断一下两组同学行走的夹角是否为直角 并说明理由;
(2)如果接下来两组同学以原来的速度相向而行,那么经过多长时间后才能相遇
9.如图,一根长度为50cm的木棒的两端系着一根长度为70 cm的绳子,现准备在绳子上找一点,然后将绳子拉直,使拉直后的绳子与木棒构成一个直角三角形且木棒为直角边,这个点将绳子分成的两段各有多长
第十七章 勾股定理
17.1 勾股定理
第 1 课时勾股定理(一)———证明、简单计算
1. B 2. C 3.10或2 4.13 5.1
6.解:正方形的面积为 100+225=325.
或
8.解:在直角三角形 ABC中,由勾股定理,得 则
故 =12.5π-24.
9.证明:∵△BCM,△BMP,△AMP 是直角三角形,∴BP =BM -MP =BC +CM -(AM -AP ) 即 .
第2课时 勾股定理(二)———实际应用
1. A 2. D 3. A 4.34 5.8
6.10 天
7.解:(1)∵AD平分∠CAB,DE⊥AB,∠C=90°,∴CD=DE.
∵CD=3,∴DE=3.
(2)在 Rt△BDE 中,BD=5,DE=3,由勾股定理,得BE=4.∴△BDE的面积为
8.解:(1)如图,作AM ⊥ BC 于点 M,
∵△ABC的面积为 84,
=84.
解得AM=8,即 BC边上的高为8.
(2)①在 Rt△ABM中, ∴CM=BC-BM=15.
在 Rt△ACM中, 由平移的性质可知,DF=AC=17.
②当AB=BE=10时,a=BE=10;当 AB=AE=10时,BE=2BM=12,则a=BE=12;
当EA=EB=a时,ME=a-6.
在 Rt△AME中, 即
解得
则当△ABE 是等腰三角形时,a 的值为 10 或 12或 .
9.解:(1
(2)由(1)可知,
17.2 勾股定理的逆定理
第 1 课时 勾股定理的逆定理(一)
———计算、判别
1. C 2. A 3.两直线平行,同位角相等4.①③④5.2n +2n 6.(1)是 (2)不是
7.解:( CD
(2)如图, =13,
∴以AB,CD,EF 三条线可以组成直角三角形.
8.(1)证明:∵∠BAC=∠DAE=90°,
∴∠BAC--∠CAD=∠DAE--∠CAD,即∠BAD=∠CAE.
在△ACE和△ABD中,
∴△ACE≌△ABD.
(2)解:由△ACE≌△ABD,可得DB=EC=4.
在 Rt△ABC中,AB=AC=2,
在△BCD中, =DB ,
∴△BCD是直角三角形,∠BCD=90°.
9.(1)证明:∵ab=ch,∴(ab) =(ch) ,即
(2)解: ,(勾股定理)
ab=ch,(面积公式推导)
∴根据勾股定理的逆定理知道以h,c+h,a+b为边构成的三角形是直角三角形.
第2课时 勾股定理的逆定理(二)———应用
1. C 2. C 3.108 4.40 5.(0,3)或(
6.解:连接 AC,在 Rt△ABC中,
∵AB=3m,BC=4m,∠B=90°,
在△ACD中,AC=5m ,CD=12 m,DA=13 m,
∴△ACD是直角三角形.
=36.
∴所需费用为36×30=1 080(元).
7.解:由题意,得OB=12×1.5=18海里,OA=16×1.5=24海里.
又∵AB=30海里,
,即
∴∠AOB=90°.
∵∠DOA=40°,∴∠BOD=50°.
则另一艘舰艇的航行方向是北偏西50°.
8.解:(1)第一组的路程是30×30=900(m),第二组的路程是40×30=1 200(m).
∴两组同学行走的夹角是直角.
(2)1 500÷(30+40)=1500÷70=21 / (min).
答:经过 后才能相遇.
9.解:如图,设 AC=x cm,则 BC=(70-x) cm.
若 AC 为斜边,则
解得 则
若 BC 为斜边,则 x) .
解得 则
故这个点将绳子分成的两段各有
17.1 勾股定理
中小学教育资源及组卷应用平台
第1 课时 勾股定理(一)——证明、简单计算
1.直角三角形两条直角边的长分别为3 和4,则斜边长为 ( )
A.4 B.5 C.6 D.10
2.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为a,较短直角边长为b,若( =21,大正方形的面积为13,则小正方形的边长为 ( )
A.
B.2
C.
D.
3.已知直角三角形的三边分别为6,8,x,则x=
4.直角三角形两条直角边的长分别为5,12,则斜边长为 ,斜边上的高为 .
5.如图,是由四个直角边分别为3和4 且全等的直角三角形拼成的“赵爽弦图”,那么阴影部分面积为 .
6.如图,求下列图形中未知正方形的面积或未知边的长度:
7.一个直角三角形一条边为7,另一条边为13,求第三边的长.
8.如图,求出图中阴影部分的面积.
9.如图,∠C=90°,AM=CM,MP⊥AB 于点 P,求证:
第2 课时 勾股定理(二)——实际应用
1.如图,图中的小正方形的边长为1,△ABC的三个顶点都在小正方形的顶点上,则△ABC的周长为 ( )
B.16
2. 如图,在Rt△ABC中,∠C =90°,将其绕B 点顺时针旋转一周,则分别以 BA,BC 为半径的圆形形成一圆环(阴影部分),为求该圆环的面积,只需测量一条线段的长度,这条线段就是( )
A. AD B. AB C. BD D. AC
3.如图,数轴上的点A表示的数是-1,点 B 表示的数是1,CB⊥AB于点B,且BC=2,以点 A 为圆心,AC 为半径画弧交数轴于点 D,则点 D 表示的数为 ( )
B.2
C.2.8
4.一个直角三角形的两条直角边分别是8cm ,15cm,斜边是17 cm,把直角边扩大到原来的2倍,那么斜边扩大到 cm.
5.如图是由4 个边长为1 的正方形构成的田字格,连接正方形的顶点在这个田字格中最多可以作出 条长度为 的线段.
6.如图,为修通铁路凿通隧道 AC,量出∠A =40°,∠B=50°,AB=5千米,BC=4千米,若每天凿隧道0.3 千米,问几天才能把隧道 AC 凿通
7.如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB 于点E,若AC=6,BC=8,CD =3.
(1)求 DE 的长;
(2)求△BDE 的面积.
8.已知:如图,△ABC的面积为84,BC=21,现将△ABC沿直线BC向右平移a(0
(2)若 AB =10,
①求线段 DF 的长;
②连接AE,当△ABE 是等腰三角形时,求 a 的值.
9.细心观察图形,认真分析各式,然后回答问题:
(1)推算出OA 的长和S 的值;
(2)用含n(n为正整数)的式子表示上述规律;
(3)求 的值.
OA =1, OA =() +1=2, OA =() +1=3, OA =() +1=4, …… s = , S = , S = , ……
17.2 勾股定理的逆定理
第1 课时 勾股定理的逆定理(一)——计算、判别
1.下列命题中,假命题的是 ( )
A.在△ABC 中,若∠B +∠C = ∠A,则△ABC是直角三角形
B.在△ABC 中,若 则△ABC 是直角三角形
C.在△ABC中,若∠A: ∠B: ∠C =6: 8:10,则△ABC 是直角三角形
D.在△ABC 中,若 a: b: c =5: 4: 3,则△ABC 是直角三角形
2.已知△ABC,AB =5,BC =12,AC =13,点 P 是AC 上一个动点,则线段 BP 长的最小值是( )
B.5 C. D.12
3.定理“同位角相等,两直线平行”的逆定理是
4.△ABC的三边长分别是a,b,c,下列条件:①∠A=∠B--∠C;②∠A: ∠B: ∠C=3:4: 5;③a: b: c=5: 12: 13;④a =(b+c)(b-c);⑤三边之长为3 ,4 ,5 ,其中能判断△ABC 是直角三角形的是 .
5.已知a,b,c是一组勾股数,其中c最大,且c=2n +2n+1,a=2n+1,则b= .(用含 n的代数式表示,其中n为正整数)
6.判断由线段a,b,c组成的三角形是不是直角三角形,并说明理由.
(2)a=13,b=14,c=15.
7.如图,在4×3的正方形网格中,每个小正方形的边长都是1.
(1)分别求出线段AB,CD的长度;
(2)在图中画线段EF,使得 以 AB,CD,EF三条线段长为边能否构成直角三角形 并说明理由.
8.如图,△ABC 和△ADE 都是等腰直角三角形,AB=AC,AD=AE,∠BAC=∠DAE=90°.
(1)求证:△ACE≌△ABD;
(2)若AC=2,EC=4,DC =2 求∠ACD的度,数.
9.如图,在△ABC 中,∠ACB=90°,CD⊥AB 于点D,∠A,∠B,∠C所对的边分别为a,b,c,斜边上的高为h.
(1)求证:
(2)判断:三边分别为h,a+b,c+h的三角形是否为直角三角形 请说明理由.
第2课时 勾股定理的逆定理(二)——应用
1.甲、乙两艘客轮同时离开港口,航行的速度都是40 m/min,甲客轮用15 min到达点 A,乙客轮用20 min到达点 B,若A,B两点的直线距离为1 000 m,甲客轮沿着北偏东30°的方向航行,则乙客轮的航行方向可能是 ( )
A.北偏西30° B.南偏西30°
C.南偏东60° D.南偏西60°
2.将直角三角形的各边都缩小或扩大同样的倍数后,得到的三角形 ( )
A.可能是锐角三角形
B.不可能是直角三角形
C.仍然是直角三角形
D.可能是钝角三角形
3.在△ABC中,若三条边的长度分别为9,12,15,则以两个这样的三角形所拼成的四边形的面积是 .
4.甲船以每小时16 海里的速度从港口A 出发向北偏东50°的方向航行,乙船以每小时12海里的速度同时从港口A 出发向南偏东方向航行,离开港口2 小时后两船相距40 海里,则乙船向南偏东 °方向航行.
5.如图,已知点A(-1,0)和点B(1,2),在y轴正半轴上确定点 P,使得△ABP 为直角三角形,则满足条件的点 P 的坐标为 .
6.如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3m,BC=4m,CD=12m,DA=13 m,∠B=90°.小区为美化环境,欲在空地上铺草坪,已知草坪每平方米30元,试问铺满这块空地共需花费多少元
7.在寻找马航MH370 航班过程中,两艘搜救舰艇接到消息,在海面上有疑似漂浮目标A,B.接到消息后,一艘舰艇以16海里/时的速度离开港口 O(如图)向北偏东40°方向航行,另一艘舰艇在同时以12 海里/时的速度向北偏西一定角度的航向行驶,已知它们离港口一个半小时后相距30 海里,问另一艘舰艇的航行方向是北偏西多少度
8.某校有两个课外小组的同学到校外去采集植物标本,已知第一组的速度为30 m/min,第二组的速度为40 m/min,且两组行走的路线为直线,半小时后,两组同学同时停下来,这时两组同学正好相距1 500 m.
(1)请你判断一下两组同学行走的夹角是否为直角 并说明理由;
(2)如果接下来两组同学以原来的速度相向而行,那么经过多长时间后才能相遇
9.如图,一根长度为50cm的木棒的两端系着一根长度为70 cm的绳子,现准备在绳子上找一点,然后将绳子拉直,使拉直后的绳子与木棒构成一个直角三角形且木棒为直角边,这个点将绳子分成的两段各有多长
第十七章 勾股定理
17.1 勾股定理
第 1 课时勾股定理(一)———证明、简单计算
1. B 2. C 3.10或2 4.13 5.1
6.解:正方形的面积为 100+225=325.
或
8.解:在直角三角形 ABC中,由勾股定理,得 则
故 =12.5π-24.
9.证明:∵△BCM,△BMP,△AMP 是直角三角形,∴BP =BM -MP =BC +CM -(AM -AP ) 即 .
第2课时 勾股定理(二)———实际应用
1. A 2. D 3. A 4.34 5.8
6.10 天
7.解:(1)∵AD平分∠CAB,DE⊥AB,∠C=90°,∴CD=DE.
∵CD=3,∴DE=3.
(2)在 Rt△BDE 中,BD=5,DE=3,由勾股定理,得BE=4.∴△BDE的面积为
8.解:(1)如图,作AM ⊥ BC 于点 M,
∵△ABC的面积为 84,
=84.
解得AM=8,即 BC边上的高为8.
(2)①在 Rt△ABM中, ∴CM=BC-BM=15.
在 Rt△ACM中, 由平移的性质可知,DF=AC=17.
②当AB=BE=10时,a=BE=10;当 AB=AE=10时,BE=2BM=12,则a=BE=12;
当EA=EB=a时,ME=a-6.
在 Rt△AME中, 即
解得
则当△ABE 是等腰三角形时,a 的值为 10 或 12或 .
9.解:(1
(2)由(1)可知,
17.2 勾股定理的逆定理
第 1 课时 勾股定理的逆定理(一)
———计算、判别
1. C 2. A 3.两直线平行,同位角相等4.①③④5.2n +2n 6.(1)是 (2)不是
7.解:( CD
(2)如图, =13,
∴以AB,CD,EF 三条线可以组成直角三角形.
8.(1)证明:∵∠BAC=∠DAE=90°,
∴∠BAC--∠CAD=∠DAE--∠CAD,即∠BAD=∠CAE.
在△ACE和△ABD中,
∴△ACE≌△ABD.
(2)解:由△ACE≌△ABD,可得DB=EC=4.
在 Rt△ABC中,AB=AC=2,
在△BCD中, =DB ,
∴△BCD是直角三角形,∠BCD=90°.
9.(1)证明:∵ab=ch,∴(ab) =(ch) ,即
(2)解: ,(勾股定理)
ab=ch,(面积公式推导)
∴根据勾股定理的逆定理知道以h,c+h,a+b为边构成的三角形是直角三角形.
第2课时 勾股定理的逆定理(二)———应用
1. C 2. C 3.108 4.40 5.(0,3)或(
6.解:连接 AC,在 Rt△ABC中,
∵AB=3m,BC=4m,∠B=90°,
在△ACD中,AC=5m ,CD=12 m,DA=13 m,
∴△ACD是直角三角形.
=36.
∴所需费用为36×30=1 080(元).
7.解:由题意,得OB=12×1.5=18海里,OA=16×1.5=24海里.
又∵AB=30海里,
,即
∴∠AOB=90°.
∵∠DOA=40°,∴∠BOD=50°.
则另一艘舰艇的航行方向是北偏西50°.
8.解:(1)第一组的路程是30×30=900(m),第二组的路程是40×30=1 200(m).
∴两组同学行走的夹角是直角.
(2)1 500÷(30+40)=1500÷70=21 / (min).
答:经过 后才能相遇.
9.解:如图,设 AC=x cm,则 BC=(70-x) cm.
若 AC 为斜边,则
解得 则
若 BC 为斜边,则 x) .
解得 则
故这个点将绳子分成的两段各有
