第十八章 平行四边形 课时强化训练 2023—2024学年人教版数学八年级下册(含答案)
文档属性
| 名称 | 第十八章 平行四边形 课时强化训练 2023—2024学年人教版数学八年级下册(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-03 00:00:00 | ||
图片预览



文档简介
第十八章 平行四边形
18.1 平行四边形
中小学教育资源及组卷应用平台
第1 课时 平行四边形的性质
1.在下列性质中,平行四边形不一定具有的是( )
A.对边相等 B.对边平行
C.对角互补 D.内角和为360°
2.在 ABCD中,∠B+∠D=260°,那么∠A的度数是 ( )
A.130° B.100° C.50° D.80°
3.如图,在平行四边形 ABCD 中,∠A =110°,则∠1 = .
4.平行四边形ABCD的周长是18,三角形ABC的周长是 14,则对角线 AC 的长是 .
5.如图,在 ABCD 中,点O 是对角线AC,BD 的交点,AC垂直于 BC,且AB=10cm,AD=8cm,则 OB= cm.
6.如图, ABCD 的对角线AC,BD 相交于点O,E,F分别是 OC,OA 的中点.求证:BE=DF.
7.如图,在 ABCD 中,∠ABC的平分线BE 交AD于点 E,∠ADC 的平分线 DF 交 BC 于点 F,AB=5,DE=3,∠ABC=50°.
(1)求∠FDC的度数;
(2)求 ABCD的周长.
8.如图,在平行四边形ABCD 中,∠B,∠C的平分线交于点 P,且分别与AD 交于点 E,F.
(1)求证:△BPC为直角三角形;
(2)若BC=16,CD=3,PE=8,求△PEF的面积.
9.如图,四边形 ABCD 为平行四边形,∠BAD 的平分线 AF 交CD于点 E,交BC 的延长线于点F.
(1)求证:BF=CD;
(2)连接BE,若 BE⊥AF,∠F=60°,BE=2 ,求AB 的长.
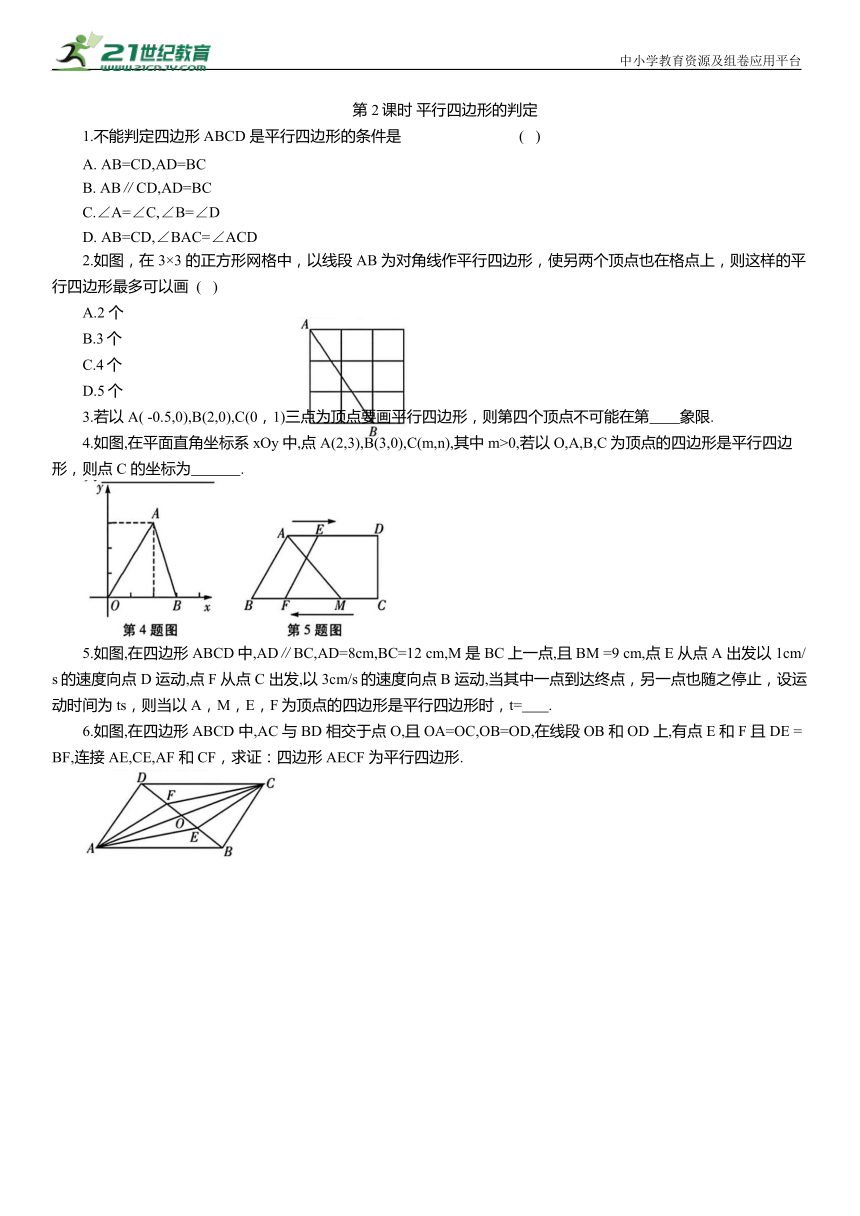
第2课时 平行四边形的判定
1.不能判定四边形ABCD 是平行四边形的条件是 ( )
A. AB=CD,AD=BC
B. AB∥CD,AD=BC
C.∠A=∠C,∠B=∠D
D. AB=CD,∠BAC=∠ACD
2.如图,在3×3 的正方形网格中,以线段AB 为对角线作平行四边形,使另两个顶点也在格点上,则这样的平行四边形最多可以画 ( )
A.2 个
B.3个
C.4个
D.5个
3.若以A( -0.5,0),B(2,0),C(0,1)三点为顶点要画平行四边形,则第四个顶点不可能在第 象限.
4.如图,在平面直角坐标系xOy中,点A(2,3),B(3,0),C(m,n),其中m>0,若以O,A,B,C为顶点的四边形是平行四边形,则点 C 的坐标为 .
5.如图,在四边形ABCD中,AD∥BC,AD=8cm,BC=12 cm,M 是 BC上一点,且 BM =9 cm,点E 从点A 出发以1cm/s的速度向点 D 运动,点F 从点 C 出发,以3cm/s的速度向点 B 运动,当其中一点到达终点,另一点也随之停止,设运动时间为ts,则当以A,M,E,F为顶点的四边形是平行四边形时,t= .
6.如图,在四边形ABCD 中,AC 与 BD 相交于点O,且OA=OC,OB=OD,在线段OB 和OD 上,有点 E 和 F 且 DE =BF,连接AE,CE,AF 和CF,求证:四边形AECF 为平行四边形.
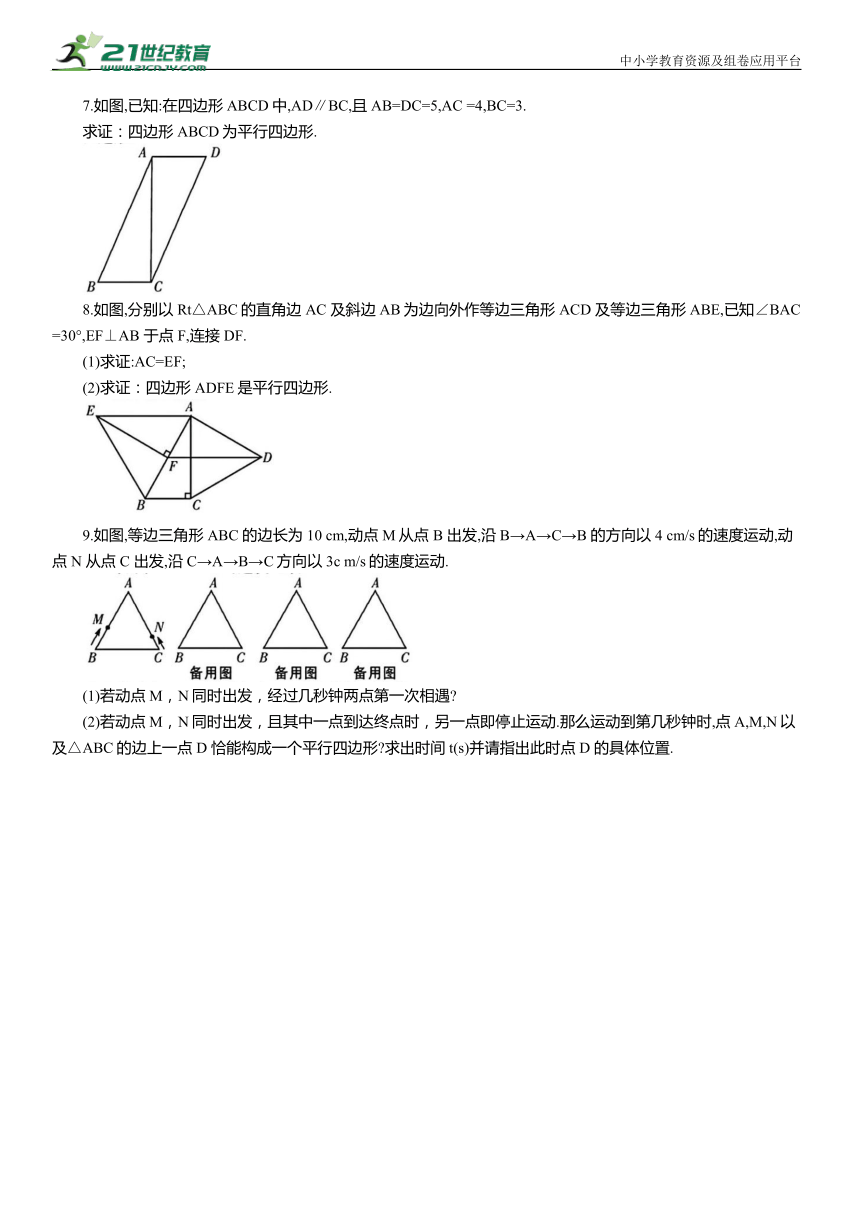
7.如图,已知:在四边形ABCD中,AD∥BC,且AB=DC=5,AC =4,BC=3.
求证:四边形 ABCD为平行四边形.
8.如图,分别以 Rt△ABC的直角边 AC 及斜边AB为边向外作等边三角形 ACD 及等边三角形ABE,已知∠BAC=30°,EF⊥AB 于点 F,连接DF.
(1)求证:AC=EF;
(2)求证:四边形ADFE是平行四边形.
9.如图,等边三角形ABC 的边长为10 cm,动点 M从点 B 出发,沿 B→A→C→B 的方向以4 cm/s的速度运动,动点 N 从点 C 出发,沿 C→A→B→C方向以3c m/s的速度运动.
(1)若动点M,N同时出发,经过几秒钟两点第一次相遇
(2)若动点M,N同时出发,且其中一点到达终点时,另一点即停止运动.那么运动到第几秒钟时,点A,M,N以及△ABC的边上一点 D 恰能构成一个平行四边形 求出时间t(s)并请指出此时点 D 的具体位置.
第3课时 三角形的中位线
1.如图,在四边形ABCD中,∠C=90°,E,F分别为AB,AD 的中点, 则EF的长为 ( )
C. D.
2.如图,在 Rt△ABC中,∠B=90°,BC=3,AB =4,点 D,E 分别是AB,AC 的中点,CF平分 Rt△ABC的一个外角∠ACM,交 DE的延长线于点 F,则DF的长为 ( )
A.4 B.5 C.5.5 D.6
3.如图,已知在△ABC中,∠ABC的平分线BE交AC于点 E,DE∥BC,如果点D 是边 AB的中点,AB=8,那么DE 的长是 .
4. 如图,在四边形ABCD 中,对角线 AC⊥BD 且AC=4,BD=8,E,F分别是边AB,CD 的中点,则EF= .
5.如图,在△ABC 中,D 为AB的中点,E 为AC 上一点, BE,CD交于点O,BE=5cm,则OE= cm.
6.如图,在△ABC中,AB=8cm,AC=5cm,AD平分∠BAC,且AD⊥CD,E 为 BC 中点,求 DE 的长.
7.如图,△ABC的中线BD,CE 相交于点O,F,G分别是 BO,CO 的中点,求证:EF∥DG,且EF= DG.
8.如图,在四边形ABCD 中,BC,AD 不平行,且∠BAD+∠ADC =270°,E,F 分别是 AD,BC 的中点,已知EF=4,求. 的值.
9.如图,在四边形ABCD中,AC,BD 相交于点O,E,F分别是AD,BC的中点,EF分别交AC,BD于M,N,且OM=ON.求证:AC=BD.
18.2特殊的平行四边形
第1 课时矩形的性质
1.如图,在矩形ABCD中,AB=3,AD=4,点E在边 BC 上,若AE平分∠BED,则 BE的长为( )
A.
C.
2.如图,点 P 是矩形ABCD 的边 AD 上的一个动点,矩形的两条边 AB,BC的长分别为6和8,那么点 P 到矩形的两条对角线AC 和 BD 的距离之和是 ( )
A. B.
C. D.不确定
3.已知:如图所示的长方形 ABCD 沿 EF 折叠至D C 位置,若 则∠AED 等于 度.
4.如图,在△ABC中,点 D,E分别是边AB,AC 的中点,AF⊥BC,垂足为点F,AF=DF=4,则BF的长为 ( )
A.4 B.8 C.2 D.4
5.如图,在矩形ABCD中,AB=3,BC=4,点E是∠ACB 的平分线与边AB的交点,则BE的长为
6.如图,在矩形ABCD 中,对角线AC 与BD 相交于点 O,点 E,F 分别是 AO,DO 的中点,连接BE,CF.
(1)求证:BE=CF;
(2)连接EF,若EF =3,∠EOF =120°,求矩形ABCD 的周长.
7.如图,已知四边形ABCD 是矩形,延长AB 至点F,连接 CF,使得 CF=AF,过点 A 作AE⊥FC于点E,求证:AD=AE.
8.如图,矩形ABCD 的对角线 AC,BD 相交于点O,点E,F在BD上,BE=DF.
(1)求证:AE=CF;
(2)若AB=3,∠AOD=120°,求矩形ABCD 的面积.
9.如图,在矩形 ABCD 中,AB =4 cm,BC =8cm ,动点 M 从点 D 出发,按折线 DCBAD 方向以2cm/s的速度运动,动点 N从点 D 出发,按折线DABCD方向以1 cm/s的速度运动.
(1)若动点M,N同时出发,经过几秒钟两点相遇
(2)若点E在线段BC上,且BE=3cm,若动点M,N同时出发,相遇时停止运动,经过几秒钟,点A,E,M,N组成平行四边形
第2课时 矩形的判定
1.如图,在平行四边形ABCD 中, 对 角 线AC,BD 相交于点 O,下列条件不能判定平行四边形ABCD 为矩形的是
A.∠ABC=90° B. AC = BD
C. AD=BC,AB∥CD D.∠BAD=∠ADC
2.如果平行四边形的四个内角的平分线能够围成一个四边形,那么这个四边形一定是( )
A.平行四边形 B.矩形
C.菱形 D.正方形
3.木工做一个长方形桌面,量得桌面的长为45cm,宽为28 cm,对角线为53 cm,这个桌面 .(填“合格”或“不合格”)
4.如图,在 ABCD 中,请添加一个条件: ,使得 ABCD成为矩形.
5.已知四边形ABCD中,AD∥BC,AC=BD,如果添加一个条件,即可判定该四边形是矩形,那么所添加的这个条件可以是 .
6.如图,DB∥AC,且 E是AC 的中点.
(1)求证:BC=DE;
(2)连接AD,BE,若∠BAC=∠C,求证:四边形DBEA是矩形.
7.如图,AB∥CD,点E,F分别在AB,CD上,连接EF.∠AEF,∠CFE的平分线交于点G,∠BEF,∠DFE的平分线交于点 H.求证:四边形 EGFH是矩形.
8.如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8 cm,AD=20 cm,BC=24 cm,P,Q 分别从A,C同时出发,向D,B运动.当一个点到达端点时,停止运动,另一个点也停止运动.
(1)如果P,Q 的速度分别为1 cm/s 和3c m/s,运动时间为t秒,则t为何值时,四边形 ABQP成为矩形
(2)如果 P 的速度为 1 cm/s,要使四边形ABQP 是矩形时其长宽之比为2:1,求Q 点运动的速度.
9.如图,在 ABCD 中,AC=8,BD=12,点E,F在对角线 BD 上,点 E 从点 B 出发以1 个单位长度每秒的速度向点 D 运动,同时点 F 从点 D 出发以相同速度向点 B 运动,到端点时运动停止,运动时间为t秒.
(1)求证:四边形AECF 为平行四边形;
(2)求t为何值时,四边形AECF 为矩形
第3 课时 菱形的性质
1.如果菱形的一边长是8,那么它的周长是( )
A.16 B.32
2.如图,在菱形ABCD中,AB=2,∠ABC = 120°,则对角线BD 等于 ( )
A.2 B.4
C.6 D.8
3.已知一个菱形的边长为2,较长的对角线长为2 ,则这个菱形的面积是 .
4. 如图,在菱形 ABCD 中,BD =4 ,∠ABC =60°,则菱形ABCD的周长等于 .
5.如图,菱形 ABCD 的对角线 AC,BD 相交于点O,过点 A 作AH⊥BC 于点 H,连接OH,若OB=4,S菱形ABCD =24,则OH的长为 .
6.如图,在菱形 ABCD 中,点 E 是边AD 上一点,延长 AB 至点 F,使 BF = AE,连接 BE,CF.求证:BE =CF.
7.如图,在菱形 ABCD中,对角线AC,BD 相交于点O,过点D 作对角线BD 的垂线交BA的延长线于点 E,若AC =8,BD=6,求 BE的长.
8.在菱形ABCD 中,∠ABC=60°,E 是对角线AC上任意一点,F 是线段BC 延长线上一点,且CF=AE,连接BE,EF.
(1)如图(1),当E 是线段AC 的中点时,求证:BE=EF;
(2)如图(2),当点 E 不是线段AC 的中点,其他条件不变时,请你判断(1)中的结论是否成立 若成立,请证明;若不成立,请说明理由.
9.如图,四边形 ABCD 为菱形,E 为对角线AC 上的一个动点(不与A,C重合),连接DE 并延长交AB的延长线于点 F,连接BE.
(1)求证:△DCE≌△BCE;
(2)求证:∠F=∠EBC;
(3)若∠DAB =90°,当△BEF 为等腰三角形时,求∠EFB的度数.
第4 课时 菱形的判定
1.如图,在△ABC 中,点 D 是BC的中点,点 E,F分别在线段AD 及其延长线上,DE = DF.在下列条件中,使四边形 BECF 是菱形的是( )
A. EB⊥EC B. AB⊥AC
C. AB=AC D. BF∥CE
2.四个点A,B,C,D 在同一平面内,从①AB∥CD;②AB=CD;③AC⊥BD;④AD = BC;⑤AD∥BC,这五个条件中任选三个,能使四边形ABCD是菱形的选法有 ( )
A.1 种 B.2种 C.3种 D.4种
3.在 ABCD中,AB=5,AC=6,当BD= 时,四边形ABCD是菱形.
4.在四边形ABCD中,AC⊥BD,AB=AD,要使四边形ABCD 是菱形,只需添加一个条件,这个条件可以是 (只要填写一种情况).
5.如图,在 Rt△ABC 中,∠ACB =90°,AC =4,BC=3,D为斜边AB上一点,以CD,CB 为边作平行四边形 CDEB,当AD = ,平行四边形 CDEB 为菱形.
6. 如图,△ABC≌△ABD,点 E 在边 AB 上,CE∥BD,连接DE.求证:
(1)∠CEB=∠CBE;
(2)四边形 BCED 是菱形.
7.如图,在△ABC中,∠BAC=90°,AD⊥BC 于点D,CE平分∠ACB,交AD于点G,交AB 于点E,EF⊥BC 于点 F,
求证:四边形AEFG 是菱形.
8.如图,已知点 P 为∠ACB 平分线上的一点,∠ACB=60°,PD⊥CA 于点 D,PE⊥CB 于点E.点 M 是线段 CP上的动点(不与两端点 C,P重合),连接DM,EM.
(1)求证:DM=EM;
(2)当点 M 运动到线段 CP 的什么位置时,四边形 PDME 为菱形,请说明理由.
9.如图,在 ABCD 中,对角线AC,BD交于点O,点E,F在BD上,且BE=DF,连接AE并延长,交BC于点 G,连接CF并延长,交AD 于点 H.
(1)求证:△AOE≌△COF;
(2)若AC 平分∠HAG,求证:四边形 AGCH 是菱形.
第5课时 正方形的性质
1.一个正方形和两个等边三角形的位置如图所示,则∠1 + ∠2+∠3 的度数为 ( )
A.150° B.120°
C.90° D.180°
2.如图,在平面直角坐标系xOy中,正方形ABCD的顶点 D 在 y 轴上,A( -3,0),B(1,b),则正方形ABCD的面积为( )
A.34 B.25 C.20 D.16
3.如图,AC 是正方形ABCD 的对角线,∠DCA 的平分线交 BA 的延长线于点 E,若AB=3,则AE= .
4.如图,将正方形 OABC 放在平面直角坐标系中,O 是原点,A 的坐标为(1, ),则点 C 的坐标为 .
5.如图,在正方形AFCE 中,D 是边CE 上一点,B是 CF 延长线上一点,且 AB =AD,若四边形ABCD的面积是24,则AC 长是 .
6.已知:如图,E 为正方形 ABCD的边BC 延长线上的点,F 是 CD 边上一点,且CE =CF,连接DE,BF,求证:DE=BF.
7.如图,在正方形ABCD中,E,F 分别是边 CD,DA 上的点,且CE =DF,AE 与BF 交于点 M.求证:AE⊥BF.
8.已知:如图,在正方形ABCD 中,点 E 为边 AB的中点,连接DE,点F 在DE上,CF=CD,过点F 作FG⊥FC 交AD于点 G.
(1)求证:GF=GD;
(2)连接AF,求证:AF⊥DE.
C
9.在正方形ABCD中,点 P 是边BC上一动点(不包含端点),线段AP 的垂直平分线与AB,AP,BD,CD分别交于点M,E,F,N.
(1)如图(1),若 PB =a,AB =3a,求线段 MN的长度;
(2)用等式表示 ME,EF,NF 之间的数量关系并证明.
第6课时 正方形的判定
1.在四边形ABCD中,∠A =∠B =∠C=90°,如果再添加一个条件,即可推出该四边形是正方形,这个条件可以是 ( )
A. BC=CD B. AB=CD
C.∠D=90° D. AD=BC
2.有下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD.从中选取两个作为补充条件,使 ABCD 为正方形(如图).现有下列四种选法,其中错误的是 ( )
A.②③
B.②④
C.①②
D.①③
3.在矩形ABCD 中,再增加条件 (只需填一个)可使矩形ABCD 成为正方形.
4.如果一个四边形的两条对角线互相平分,互相垂直且相等,那么这个四边形是 .
5.如图,以△ABC 的三边为边分别作等边△ACD,△ABE,△BCF,则下列结 论: ① △EBF ≌△DFC; ② 四 边 形AEFD 为平行四边形;③当AB = AC,∠BAC =120°时,四边形 AEFD是正方形.其中正确的结论是 .(请写出正确结论的序号).
6.如图,在平面直角坐标系中,四边形ABCD 的顶点坐标分别是A( -2,0),B(0,-2),C(2,0),D(0,2),求证:四边形 ABCD是正方形.
7.如图,在 ABCD 中,对角线AC,BD交于点O,E 是 BD 延长线上的点,且△ACE是等边三角形.
(1)求证:四边形 ABCD 是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD 是正方形.
8.如图,菱形 ABCD 的对角线 AC,BD 相交于点O,分别延长OA,OC 到点 E,F,使AE=CF,依次连接B,F,D,E各点.
(1)求证:△BAE≌△BCF;
(2)若∠ABC =40°,则当∠EBA = °时,四边形BFDE 是正方形.
9. 如图,AD 是△ABC 的角平分线,线段 AD 的垂直平分线分别交AB和AC 于点E,F,连接DE,DF.
(1)试判定四边形 AEDF 的形状,并证明你的结论;
(2)若DE =13,EF=10,求AD 的长;
(3)△ABC满足什么条件时,四边形 AEDF 是正方形
第十八章 平行四边形
18.1平行四边形
第 1 课时 平行四边形的性质
1. C 2. C 3.70° 4.5 5. 3
6.证明:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD.
∵E,F分别是OC,OA的中点,
又∠BOE=∠DOF,∴△BOE≌△DOF.
∴BE=DF.
7.解:(1)∵在□ABCD中,∠ABC=50°,∴∠ADC=∠ABC=50°.
∵DF平分∠ADC,∴∠FDC= ∠ADC=25°.
(2)四边形ABCD是平行四边形,
∴AE∥BC.∴∠AEB=∠CBE.
∵BE平分∠ABC,∴∠ABE=∠CBE.
∴∠ABE=∠AEB.∴AE=AB=5.
∵DE=3,∴AD=AE+DE=8.
∴□ABCD的周长=2(AB+AD)=2(5+8)=26.
8.(1)证明:∵四边形ABCD为平行四边形,∴AB∥CD.
∴∠ABC+∠BCD=180°.
∵∠B,∠C的平分线交于点P,
∴∠BPC=90°,即△BPC为直角三角形.
(2)解:∵四边形ABCD为平行四边形,∴AD∥CB.
∴∠CBE=∠BEA,∠BCF=∠CFD.
∴∠ABE=∠BEA,∠DCF=∠CFD.
∴AB=AE=3,CD=DF=3.
∴EF=10.
在 Rt△PEF中,PE=8,EF=10,∴PF=6.
∴△PEF的面积是 24.
9.(1)证明:∵四边形ABCD为平行四边形,
∴AB=CD,AD∥BC.∴∠F=∠DAF.
又∵AF平分∠BAD,∴∠BAE=∠DAF.
∴∠F=∠BAE.
∴AB=BF.∴BF=CD.
(2)解:∵AB=BF,∠F=60°,
∴△ABF 为等边三角形.
∵BE⊥AF,∠F=60°,
∴∠BEF=90°,∠EBF=30°.
在 Rt△BEF中,设EF=x,则 FB=2x.
∴x=2.∴AB=BF=4.
第2 课时 平行四边形的判定
1. B 2. D 3.三 4.(5,3)或(1,-3) 5. 或
6.证明:∵DE=BF,OB=OD,
∴DE-OD=BF-OB.即OE=OF.
又∵OA=OC,∴四边形AECF是平行四边形.
7.证明:∵AB=5,AC=4,BC=3,
∴AB =AC +BC .∴∠BCA=90°.
∵AD∥BC,∴∠DAC=∠BCA=90°.
∵DC=5,AC=4,∴AD =DC -AC =9.
∴AD=BC=3.
∴四边形 ABCD 为平行四边形.
8.证明:(1)∵△BAE是等边三角形,EF⊥AB,
∴∠AEF= ∠AEB=30°,AE=AB,∠EFA=90°.
∵∠ACB=90°,∠BAC=30°,
∴∠AEF=∠BAC,∠EFA=∠ACB.
在△AEF 和△BAC中,
∴△AEF≌△BAC.∴AC=EF.
(2)∵△ACD是等边三角形,
∴AC=AD,∠DAC=60°.
由(1)的结论,得AC=EF.∴AD=EF.
∵∠BAC=30°,
∴∠FAD=∠BAC+∠DAC=90°.
∵∠EFA=90°,∴AD∥EF.
∵AD=EF,
∴四边形ADFE是平行四边形.
9.解:(1)第一次相遇时间 (秒).
(2)当点 M在线段AB 上,点 N 在AC 上时,点 D 在BC上,
∵四边形ANDM为平行四边形,
DM=AN,DM∥AN,
∵△ABC为等边三角形,△BMD和△NCD是等边三角形,
∴BM+CN=CN+AN=10.
此时
当点 M在线段AC 上,点 N 在AB 上时,同理△BND和△MCD是等边三角形.
AM=4t-10,AN=3t-10,
∴AM+AN=AC=10,4t-10+3t-10=10, 此时
当点 M在线段 BC 上,点 N在 AB 上时,点 D 在 AC上,同理△AND和△MCD是等边三角形,CM=4t-20,AN=3t-10,
∴CM=AN.
∴4t-20=3t-10,t=10,不合题意.
综上所述,当 时,点 D 在 BC 上, 当t= 时,点 D在BC上,
第 3 课时 三角形的中位线
1. D 2. A 3.4 4.2 5.1.25
6.解:如图,延长CD交AB于点F,
∵AD平分∠BAC,
∴∠CAD=∠FAD.
∵AD⊥CD,
∴∠ADC=∠ADF=90°.
在△ACD和△AFD中,
∴△ACD≌△AFD.
∴CD=DF,AF=AC=5cm.
∵E为BC 中点,BF=AB-AF=8-5=3,
7.证明:如图,连接 DE,FG,∵BD,CE 是△ABC 的中线,
∴D,E 是 AC,AB 的中点.
∴DE∥BC,
同理:FG∥BC,
∴DE∥FG,DE=FG.
∴四边形 DEFG 是平行四边形.
∴EF∥DG,EF=DG.
解:如图,连接BD,取 BD 的中点M,连接EM 并延长交 BC 于点 N,连接 FM,
∵∠BAD+∠ADC=270°,∴∠ABC+∠C=90°.
∵E,F,M分别是AD,BC,BD的中点,
∴∠MNF=∠ABC,∠MFN=∠C.
∴∠MNF+∠MFN=90°,即∠NMF=90°.
由勾股定理,得ME +MF =EF =16.
9.证明:如图,取 CD 的中点G,连接 EG,FG.
∵E,F 分别是 AD, BC 的中点,
∴∠OMN=∠GEF,∠ONM=∠GFE.
∵OM=ON,∴∠OMN=∠ONM.
∴∠GEF=∠GFE.∴EG=FG.
∴AC=BD.
18.2 特殊的平行四边形
第 1 课时 矩形的性质
1. D 2. C 3.50 4. D 5.
6.(1)证明:∵四边形 ABCD是矩形,∴OB=OD=OC=OA.
∵点 E,F分别是AO,DO的中点,
∵∠BOE=∠COF,∴△BOE≌△COF.
∴BE=CF.
(2)解:∵点E,F分别是AO,DO的中点,∴AD=2EF=6.
∵∠AOD=120°,AO=OD,
∴∠ODA=30°.
在 Rt△ADB中,设 AB=x,则 BD=2x,由 (2x) ,得.
∴矩形的周长为
7.证明:连接AC,如图.
∵CF=AF,
∴∠FCA=∠CAF.
∵四边形 ABCD 是矩形,
∴DC∥AB.
∴∠DCA=∠CAF.
∴∠FCA=∠DCA.
∵AE⊥FC,
∴∠CEA=90°.
∴∠CDA=∠CEA=90°.
在△ADC和△AEC 中,
∴△ADC≌△AEC(AAS).
∴AD=AE.
8.(1)证明:∵四边形ABCD 是矩形,
∴OA=OC=OB=OD,AC=BD,∠ABC=90°.
∵BE=DF,∴OE=OF.
在△AOE 和△COF中,
∴△AOE≌△COF(SAS).∴AE=CF.
(2)解:∵OA=OC,OB=OD,AC=BD,∴OA=OB.
∵∠AOB=∠COD=60°,∴△AOB是等边三角形.
∴OA=AB=3.∴AC=2OA=6.
在 Rt△ABC中,
∴矩形ABCD的面积=
9.解:(1)设ts时两点相遇,根据题意,得t+2t=2(4+8).解得 t=8.
答:经过8 s两点相遇.
答:经过8s两点相遇M不可能在AB 或DC卡.
①如图(1),点 M在E 点右侧时,当AN=ME 时,四边形 AEMN为平行四边形,得8-t=9-2t.解得 t=1.
∵t=1时,点 M 还在 DC 上,
∴t=1 舍去.
②如图(2),点 M在E 点左侧时,当AN=ME时,四边形 ANEM 为平行四边形,得8-t=2t-9.
解得
∴经过 s,点 A,E,M,N 组成平行四边形.
第 2 课时 矩形的判定
1. C 2. B 3.合格 4.∠A=90°(答案不唯一)
5. AD=BC(或AB∥CD,答案不唯一)
6.证明:(1)∵E是AC中点,∴
又∵DB∥EC,
∴四边形 DBCE 是平行四边形.
∴BC=DE.
(2)如图,
∵DB∥AE,DB=AE,
∴四边形 DBEA 是平行四边形.
∵∠BAC=∠C,
∴BA=BC.
∵BC=DE,∴AB=DE.
∴□DBEA是矩形.
7.证明:∵∠AEF,∠CFE的平分线交于点G,
∵AB∥CD,∴∠AEF+∠CFE=180°.
∴∠G=90°.
同理可得∠H=90°.
∵EG,EH分别是∠AEF,∠BEF的平分线,
∴四边形 EGFH 是矩形.
8.解:(1)由题意得 AP=t,BQ=24-3t.
要使四边形ABQP 为矩形,只需 AP=BQ,由t=24-3t,解得t=6.
∴当t=6时,四边形ABQP 成为矩形.
(2)设Q点运动的速度为x cm/s,当运动时间为 ts时,四边形 ABQP 是矩形时其长宽之比为2:1.
∵四边形 APQB是矩形且其长宽之比为2: 1,AB=8cm ,
∴PA=BQ=4 cm或PA=BQ=16 cm.
∴t=24-tx=4或t=24-tx=16.
解得x=5或
∴要使四边形APQB 是矩形时其长宽之比为 2:1,Q点运动的速度为5cm/s或
(1)证明:在□ABCD中,∵AD∥BC,AD=BC,∴∠EBC=∠ADF.由题意知,BE=DF,
在△BEC与△DFA中.
∴△BEC≌△DFA(SAS).
∴CE=AF.同理可得:AE=CF.
∴四边形 AECF 为平行四边形.
(2)解:当t=2或t=10时,四边形AECF为矩形.理由如下:如图,由矩形的性质知,OE=OF,OA=OC,要使∠EAF 是直角,只需
则∠1=∠2,∠3=∠4.
∵∠1+∠2+∠3+∠4=180°,
∴2∠2+2∠3=180°.
∴∠2+∠3=90°,即∠EAF=90°.
此时 或BE=DF=12-2=10cm.
第3 课时 菱形的性质
1. B 2. A 3.2 4.16 5.3
6.证明:∵四边形ABCD是菱形,
∴AB=BC,AD∥BC.∴∠A=∠CBF.
在△ABE 和△BCF 中
∴△ABE≌△BCF(SAS).
∴BE=CF.
7.解:∵四边形ABCD是菱形,∴AB∥CD,AC⊥BD.
∴AE∥CD,∠AOB=90°.
∵DE⊥BD,即∠EDB=90°,∴∠AOB=∠EDB.
∴DE∥AC.
∴四边形 ACDE 是平行四边形.
∵四边形 ABCD是菱形,AC=8,BD=6,
∴AO=4,DO=3,AD=CD=5.
∵四边形 ACDE是平行四边形,∴AE=CD=5.
∴BE=AE+AB=10.
8.(1)证明:∵四边形ABCD是菱形,∴AB=BC.
∵∠ABC=60°,∴△ABC是等边三角形.
∴∠BCA=60°.
∵E 是线段AC 的中点,
∴∠CBE=∠ABE=30°,AE=CE.
∵CF=AE,∴CE=CF.
∴∠CBE=∠F=30°.
∴BE=EF.
(2)解:结论成立.
理由如下:过点 E作EG∥BC交AB 于点G,如图.
∵四边形 ABCD 为菱形,∠ABC=60°,
∴AB=BC,∠BCD=120°,AB∥CD.
∴∠ACD=60°,∠DCF=∠ABC=60°.
∴∠ECF=120°.
又∵∠ABC=60°,∴△ABC是等边三角形.
∴AB=AC,∠ACB=60°.
又∵EG∥BC,∴∠AGE=∠ABC=60°.
又∵∠BAC=60°,∴△AGE是等边三角形.
∴AG=AE=GE,∠AGE=60°.
∴BG=CE,∠BGE=120°=∠ECF.
又∵CF=AE,∴GE=CF.
在△BGE和△ECF中,
∴△BGE≌△ECF(SAS).
∴BE=EF.
9.(1)证明:∵四边形ABCD是菱形,∴CD=CB,∠ACD=∠ACB.
在△DCE 和△BCE 中,
∴△DCE≌△BCE(SAS).
(2)证明:∵△DCE≌△BCE,∴∠CDE=∠CBE.
∵CD∥AB,∴∠CDE=∠F.
∴∠F=∠EBC.
(3)解:∵∠EBF为钝角,∴只能是 BE=BF.
设∠BEF=∠BFE=x°,
可通过三角形内角和为180°,得90+x+x+x=180,解得x=30.
∴∠EFB=30°.
第 4 课时 菱形的判定
1. C 2. D 3.8 4. AB∥CD(答案不唯一) 5.
6.证明:(1)∵△ABC≌△ABD,∴∠ABC=∠ABD.
∵CE∥BD,∴∠CEB=∠DBE.
∴∠CEB=∠CBE.
(2)∵△ABC≌△ABD,∴BC=BD.
∵∠CEB=∠CBE,∴CE=CB.
∴CE=BD.
∵CE∥BD,
∴四边形 BCED 是平行四边形.
∵BC=BD,
∴四边形 BCED 是菱形.
7.证明:∵AD⊥BC,∴∠ADB=90°.
∴∠B+∠BAD=90°.
∵∠BAC=90°,∴∠BAD+∠CAD=90°.
∴∠B=∠CAD.
∵CE平分∠ACB,EF⊥BC,∠BAC=90°(EA⊥CA),
∴AE=EF(角平分线上的点到角两边的距离相等).
∵CE=CE,∴由勾股定理,得AC=CF.
∵△ACG和△FCG中
∴△ACG≌△FCG.∴∠CAD=∠CFG.
∵∠B=∠CAD,∴∠B=∠CFG.
∴GF∥AB.
∵AD⊥BC,EF⊥BC,∴AD∥EF.
∴AG∥EF,AE∥GF.
∴四边形 AEFG 是平行四边形.
∵AE=EF,
∴平行四边形 AEFG是菱形.
8.(1)证明:∵点 P为∠ACB平分线上的一点,
∴∠ACP=∠BCP=30°.
∵PD⊥CA 于点 D,PE⊥CB于点E,
∴PD=PE.
在 Rt△DCP 和Rt△ECP 中,
∴Rt△DCP≌Rt△ECP.∴CD=CE.
在△DCM和△ECM 中.
∴△DCM≌△ECM.∴DM=EM.
(2)解:当点 M 运动到线段 CP 的中点时,四边形PDME为菱形.
理由如下:∵∠DCP=30°,
∴PC=2PD,∠CPD=60°.
∵PD=PE,MD=ME,
∴当 DM=DP 时,PD=PE=MD=ME,则四边形DMEP 为菱形.
此时△PDM为等边三角形,∴PD=PM.
∴CM=PM.
∴当点 M运动到线段CP 的中点时,四边形 PDME为菱形.
9.证明:(1)∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵BE=DF,∴OE=OF.在△AOE 与△COF 中. ∴△AOE≌△COF(SAS).
(2)由(1),得△AOE≌△COF.
∴∠OAE=∠OCF.∴AE∥CF.
∵AH∥CG,
∴四边形 AGCH是平行四边形.
∵AC平分∠HAG,∴∠HAC=∠GAC.
∵AH∥CG,∴∠HAC=∠GCA.
∴∠GAC=∠GCA.∴CG=AG.
∴四边形 AGCH是菱形.
第 5 课时 正方形的性质
1. A 2. B 3.3 4.(- ,1). 5.4
6.证明:∵四边形ABCD 是正方形,
∴BC=DC,∠BCD=90°.
∵E为BC 延长线上的点,∴∠DCE=90°.
∴∠BCD=∠DCE.
在△BCF和△DCE中.
∴△BCF≌△DCE(SAS).
∴DE=BF.
7.证明:∵四边形ABCD 是正方形,
∴AD=CD=AB,∠D=∠BAD=90°.
∵DF=CE,
∴AD-DF=CD-CE,即 AF=DE.
在△ABF 和△DAE中,
∴△ABF≌△DAE.∴∠DAE=∠ABF.
∴∠AMF=∠ABF+∠BAE
=∠DAE+∠BAE=∠BAD=90°.
∴AE⊥BF.
8.证明:(1)∵四边形ABCD是正方形,
∴∠ADC=90°.
∵FG⊥FC,∴∠GFC=90°.
∵CF=CD,∴∠CDF=∠CFD.
∴∠GFC-∠CFD=∠ADC-∠CDF,即∠GFD=∠GDF.
∴GF=GD.
(2)连接CG.
∵CF=CD,GF=GD,
∴点G,C 在线段 FD 的中垂线上.
∴GC⊥DE,∴∠CDF+∠DCG=90°.
∵∠CDF+∠ADE=90°,
∴∠DCG=∠ADE.
∵四边形 ABCD是正方形,
∴AD=DC,∠DAE=∠CDG=90°.
∴△DAE≌△CDG.
∴AE=DG.
∵点E是边AB 的中点,
∴点 G 是边 AD 的中点.
∴AG=GD=GF.
∴∠DAF=∠AFG,∠GDF=∠GFD.
∵∠DAF+∠AFG+∠GFD+∠GDF=180°,
∴2∠AFG+2∠GFD=180°.
∴∠AFD=90°,即AF⊥DE.
9.解:(1)如图(1),过 N作 NG⊥AB,交 AB于点G.
易得四边形 AGND是矩形,∴NG=AD=AB=3a.
∵MN⊥AP,∴∠MNG=∠PAB.
又∠PBA=∠NGM,AB=NG,
∴△ABP≌△NGM.
(2)如图(2),过 P 作 PH∥AB交 MN 于点 H,过 F 作ST∥AB交BC,AD于点S,T,连接AF,PF.
∵NM垂直平分AP,∴AE=PE,∠AEM=∠PEH=90°.
∵PH∥AB,∴∠PHE=∠MEA,∠HPE=∠MAE.
∴△AME≌△PHE.∴ME=HE.
∵∠TDF=∠FBP=45°,∴TD=TF,FS=BS.
∴BS=AT=FS.
∵点 F 在线段AP 的垂直平分线上,∴FP=FA.
∴Rt△FPS≌Rt△ATF.
∴PS=TF=TD=SC.
∵PH∥TS∥CD,∴HF=FN.
∴ME+NF=EF.
第6 课时正方形的判定
1. A 2. C 3. AB=BC(答案不唯一)
4.正方形 5.①②
6.解:∵四边形ABCD的顶点坐标分别是A(--2,0),B(0,-2),C(2,0),D(0,2),
∴OA=OB=OC=OD=2,
即OA=OC,OB=OD 且AC=BD=4.
又∵AC⊥BD,
∴四边形 ABCD是正方形.
7.证明:(1)∵□ABCD,∴AO=OC.
∵△ACE 是等边三角形,
∴EO⊥AC(三线合一),即 BD⊥AC.
∴□ABCD是菱形.
(2)∵△ACE是等边三角形,
由(1)知,EO⊥AC,AO=OC,
∴∠EAO=60°,∠AEO=30°.
∵∠AED=2∠EAD,∴∠EAD=15°.
∴∠DAO=∠EAO-∠EAD=45°.
∵□ABCD是菱形,
∴∠BAD=2∠DAO=90°.
∴菱形ABCD是正方形.
8.(1)证明:∵四边形ABCD是菱形,
∴AB=CB.∴∠BAC=∠BCA.
∴180°—∠BAC=180°-∠BCA,
即∠BAE=∠BCF.
在△BAE 和△BCF 中,
∴△BAE≌△BCF(SAS).
(2)25
9.解:(1)四边形 AEDF是菱形.
理由如下:∵AD 平分∠BAC,∴∠1=∠2.
又∵EF⊥AD,∴∠AOE=∠AOF=90°.
∵在△AEO和△AFO中,
∴△AEO≌△AFO(ASA).∴EO=FO.
∵EF垂直平分AD,∴EF,AD相互平分.
∴四边形 AEDF 是平行四边形.又 EF⊥AD,
∴平行四边形AEDF为菱形.
(2)∵四边形 AEDF 是菱形,EF=10,
在 Rt△DOE 中,∵DE=13,
∴AD=2OD=24.
(3)在△ABC 中,当∠BAC=90°时,四边形 AEDF 是正方形.
∵∠BAC=90°,
∴四边形 AEDF 是正方形(有一个角是直角的菱形是正方形).
18.1 平行四边形
中小学教育资源及组卷应用平台
第1 课时 平行四边形的性质
1.在下列性质中,平行四边形不一定具有的是( )
A.对边相等 B.对边平行
C.对角互补 D.内角和为360°
2.在 ABCD中,∠B+∠D=260°,那么∠A的度数是 ( )
A.130° B.100° C.50° D.80°
3.如图,在平行四边形 ABCD 中,∠A =110°,则∠1 = .
4.平行四边形ABCD的周长是18,三角形ABC的周长是 14,则对角线 AC 的长是 .
5.如图,在 ABCD 中,点O 是对角线AC,BD 的交点,AC垂直于 BC,且AB=10cm,AD=8cm,则 OB= cm.
6.如图, ABCD 的对角线AC,BD 相交于点O,E,F分别是 OC,OA 的中点.求证:BE=DF.
7.如图,在 ABCD 中,∠ABC的平分线BE 交AD于点 E,∠ADC 的平分线 DF 交 BC 于点 F,AB=5,DE=3,∠ABC=50°.
(1)求∠FDC的度数;
(2)求 ABCD的周长.
8.如图,在平行四边形ABCD 中,∠B,∠C的平分线交于点 P,且分别与AD 交于点 E,F.
(1)求证:△BPC为直角三角形;
(2)若BC=16,CD=3,PE=8,求△PEF的面积.
9.如图,四边形 ABCD 为平行四边形,∠BAD 的平分线 AF 交CD于点 E,交BC 的延长线于点F.
(1)求证:BF=CD;
(2)连接BE,若 BE⊥AF,∠F=60°,BE=2 ,求AB 的长.
第2课时 平行四边形的判定
1.不能判定四边形ABCD 是平行四边形的条件是 ( )
A. AB=CD,AD=BC
B. AB∥CD,AD=BC
C.∠A=∠C,∠B=∠D
D. AB=CD,∠BAC=∠ACD
2.如图,在3×3 的正方形网格中,以线段AB 为对角线作平行四边形,使另两个顶点也在格点上,则这样的平行四边形最多可以画 ( )
A.2 个
B.3个
C.4个
D.5个
3.若以A( -0.5,0),B(2,0),C(0,1)三点为顶点要画平行四边形,则第四个顶点不可能在第 象限.
4.如图,在平面直角坐标系xOy中,点A(2,3),B(3,0),C(m,n),其中m>0,若以O,A,B,C为顶点的四边形是平行四边形,则点 C 的坐标为 .
5.如图,在四边形ABCD中,AD∥BC,AD=8cm,BC=12 cm,M 是 BC上一点,且 BM =9 cm,点E 从点A 出发以1cm/s的速度向点 D 运动,点F 从点 C 出发,以3cm/s的速度向点 B 运动,当其中一点到达终点,另一点也随之停止,设运动时间为ts,则当以A,M,E,F为顶点的四边形是平行四边形时,t= .
6.如图,在四边形ABCD 中,AC 与 BD 相交于点O,且OA=OC,OB=OD,在线段OB 和OD 上,有点 E 和 F 且 DE =BF,连接AE,CE,AF 和CF,求证:四边形AECF 为平行四边形.
7.如图,已知:在四边形ABCD中,AD∥BC,且AB=DC=5,AC =4,BC=3.
求证:四边形 ABCD为平行四边形.
8.如图,分别以 Rt△ABC的直角边 AC 及斜边AB为边向外作等边三角形 ACD 及等边三角形ABE,已知∠BAC=30°,EF⊥AB 于点 F,连接DF.
(1)求证:AC=EF;
(2)求证:四边形ADFE是平行四边形.
9.如图,等边三角形ABC 的边长为10 cm,动点 M从点 B 出发,沿 B→A→C→B 的方向以4 cm/s的速度运动,动点 N 从点 C 出发,沿 C→A→B→C方向以3c m/s的速度运动.
(1)若动点M,N同时出发,经过几秒钟两点第一次相遇
(2)若动点M,N同时出发,且其中一点到达终点时,另一点即停止运动.那么运动到第几秒钟时,点A,M,N以及△ABC的边上一点 D 恰能构成一个平行四边形 求出时间t(s)并请指出此时点 D 的具体位置.
第3课时 三角形的中位线
1.如图,在四边形ABCD中,∠C=90°,E,F分别为AB,AD 的中点, 则EF的长为 ( )
C. D.
2.如图,在 Rt△ABC中,∠B=90°,BC=3,AB =4,点 D,E 分别是AB,AC 的中点,CF平分 Rt△ABC的一个外角∠ACM,交 DE的延长线于点 F,则DF的长为 ( )
A.4 B.5 C.5.5 D.6
3.如图,已知在△ABC中,∠ABC的平分线BE交AC于点 E,DE∥BC,如果点D 是边 AB的中点,AB=8,那么DE 的长是 .
4. 如图,在四边形ABCD 中,对角线 AC⊥BD 且AC=4,BD=8,E,F分别是边AB,CD 的中点,则EF= .
5.如图,在△ABC 中,D 为AB的中点,E 为AC 上一点, BE,CD交于点O,BE=5cm,则OE= cm.
6.如图,在△ABC中,AB=8cm,AC=5cm,AD平分∠BAC,且AD⊥CD,E 为 BC 中点,求 DE 的长.
7.如图,△ABC的中线BD,CE 相交于点O,F,G分别是 BO,CO 的中点,求证:EF∥DG,且EF= DG.
8.如图,在四边形ABCD 中,BC,AD 不平行,且∠BAD+∠ADC =270°,E,F 分别是 AD,BC 的中点,已知EF=4,求. 的值.
9.如图,在四边形ABCD中,AC,BD 相交于点O,E,F分别是AD,BC的中点,EF分别交AC,BD于M,N,且OM=ON.求证:AC=BD.
18.2特殊的平行四边形
第1 课时矩形的性质
1.如图,在矩形ABCD中,AB=3,AD=4,点E在边 BC 上,若AE平分∠BED,则 BE的长为( )
A.
C.
2.如图,点 P 是矩形ABCD 的边 AD 上的一个动点,矩形的两条边 AB,BC的长分别为6和8,那么点 P 到矩形的两条对角线AC 和 BD 的距离之和是 ( )
A. B.
C. D.不确定
3.已知:如图所示的长方形 ABCD 沿 EF 折叠至D C 位置,若 则∠AED 等于 度.
4.如图,在△ABC中,点 D,E分别是边AB,AC 的中点,AF⊥BC,垂足为点F,AF=DF=4,则BF的长为 ( )
A.4 B.8 C.2 D.4
5.如图,在矩形ABCD中,AB=3,BC=4,点E是∠ACB 的平分线与边AB的交点,则BE的长为
6.如图,在矩形ABCD 中,对角线AC 与BD 相交于点 O,点 E,F 分别是 AO,DO 的中点,连接BE,CF.
(1)求证:BE=CF;
(2)连接EF,若EF =3,∠EOF =120°,求矩形ABCD 的周长.
7.如图,已知四边形ABCD 是矩形,延长AB 至点F,连接 CF,使得 CF=AF,过点 A 作AE⊥FC于点E,求证:AD=AE.
8.如图,矩形ABCD 的对角线 AC,BD 相交于点O,点E,F在BD上,BE=DF.
(1)求证:AE=CF;
(2)若AB=3,∠AOD=120°,求矩形ABCD 的面积.
9.如图,在矩形 ABCD 中,AB =4 cm,BC =8cm ,动点 M 从点 D 出发,按折线 DCBAD 方向以2cm/s的速度运动,动点 N从点 D 出发,按折线DABCD方向以1 cm/s的速度运动.
(1)若动点M,N同时出发,经过几秒钟两点相遇
(2)若点E在线段BC上,且BE=3cm,若动点M,N同时出发,相遇时停止运动,经过几秒钟,点A,E,M,N组成平行四边形
第2课时 矩形的判定
1.如图,在平行四边形ABCD 中, 对 角 线AC,BD 相交于点 O,下列条件不能判定平行四边形ABCD 为矩形的是
A.∠ABC=90° B. AC = BD
C. AD=BC,AB∥CD D.∠BAD=∠ADC
2.如果平行四边形的四个内角的平分线能够围成一个四边形,那么这个四边形一定是( )
A.平行四边形 B.矩形
C.菱形 D.正方形
3.木工做一个长方形桌面,量得桌面的长为45cm,宽为28 cm,对角线为53 cm,这个桌面 .(填“合格”或“不合格”)
4.如图,在 ABCD 中,请添加一个条件: ,使得 ABCD成为矩形.
5.已知四边形ABCD中,AD∥BC,AC=BD,如果添加一个条件,即可判定该四边形是矩形,那么所添加的这个条件可以是 .
6.如图,DB∥AC,且 E是AC 的中点.
(1)求证:BC=DE;
(2)连接AD,BE,若∠BAC=∠C,求证:四边形DBEA是矩形.
7.如图,AB∥CD,点E,F分别在AB,CD上,连接EF.∠AEF,∠CFE的平分线交于点G,∠BEF,∠DFE的平分线交于点 H.求证:四边形 EGFH是矩形.
8.如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8 cm,AD=20 cm,BC=24 cm,P,Q 分别从A,C同时出发,向D,B运动.当一个点到达端点时,停止运动,另一个点也停止运动.
(1)如果P,Q 的速度分别为1 cm/s 和3c m/s,运动时间为t秒,则t为何值时,四边形 ABQP成为矩形
(2)如果 P 的速度为 1 cm/s,要使四边形ABQP 是矩形时其长宽之比为2:1,求Q 点运动的速度.
9.如图,在 ABCD 中,AC=8,BD=12,点E,F在对角线 BD 上,点 E 从点 B 出发以1 个单位长度每秒的速度向点 D 运动,同时点 F 从点 D 出发以相同速度向点 B 运动,到端点时运动停止,运动时间为t秒.
(1)求证:四边形AECF 为平行四边形;
(2)求t为何值时,四边形AECF 为矩形
第3 课时 菱形的性质
1.如果菱形的一边长是8,那么它的周长是( )
A.16 B.32
2.如图,在菱形ABCD中,AB=2,∠ABC = 120°,则对角线BD 等于 ( )
A.2 B.4
C.6 D.8
3.已知一个菱形的边长为2,较长的对角线长为2 ,则这个菱形的面积是 .
4. 如图,在菱形 ABCD 中,BD =4 ,∠ABC =60°,则菱形ABCD的周长等于 .
5.如图,菱形 ABCD 的对角线 AC,BD 相交于点O,过点 A 作AH⊥BC 于点 H,连接OH,若OB=4,S菱形ABCD =24,则OH的长为 .
6.如图,在菱形 ABCD 中,点 E 是边AD 上一点,延长 AB 至点 F,使 BF = AE,连接 BE,CF.求证:BE =CF.
7.如图,在菱形 ABCD中,对角线AC,BD 相交于点O,过点D 作对角线BD 的垂线交BA的延长线于点 E,若AC =8,BD=6,求 BE的长.
8.在菱形ABCD 中,∠ABC=60°,E 是对角线AC上任意一点,F 是线段BC 延长线上一点,且CF=AE,连接BE,EF.
(1)如图(1),当E 是线段AC 的中点时,求证:BE=EF;
(2)如图(2),当点 E 不是线段AC 的中点,其他条件不变时,请你判断(1)中的结论是否成立 若成立,请证明;若不成立,请说明理由.
9.如图,四边形 ABCD 为菱形,E 为对角线AC 上的一个动点(不与A,C重合),连接DE 并延长交AB的延长线于点 F,连接BE.
(1)求证:△DCE≌△BCE;
(2)求证:∠F=∠EBC;
(3)若∠DAB =90°,当△BEF 为等腰三角形时,求∠EFB的度数.
第4 课时 菱形的判定
1.如图,在△ABC 中,点 D 是BC的中点,点 E,F分别在线段AD 及其延长线上,DE = DF.在下列条件中,使四边形 BECF 是菱形的是( )
A. EB⊥EC B. AB⊥AC
C. AB=AC D. BF∥CE
2.四个点A,B,C,D 在同一平面内,从①AB∥CD;②AB=CD;③AC⊥BD;④AD = BC;⑤AD∥BC,这五个条件中任选三个,能使四边形ABCD是菱形的选法有 ( )
A.1 种 B.2种 C.3种 D.4种
3.在 ABCD中,AB=5,AC=6,当BD= 时,四边形ABCD是菱形.
4.在四边形ABCD中,AC⊥BD,AB=AD,要使四边形ABCD 是菱形,只需添加一个条件,这个条件可以是 (只要填写一种情况).
5.如图,在 Rt△ABC 中,∠ACB =90°,AC =4,BC=3,D为斜边AB上一点,以CD,CB 为边作平行四边形 CDEB,当AD = ,平行四边形 CDEB 为菱形.
6. 如图,△ABC≌△ABD,点 E 在边 AB 上,CE∥BD,连接DE.求证:
(1)∠CEB=∠CBE;
(2)四边形 BCED 是菱形.
7.如图,在△ABC中,∠BAC=90°,AD⊥BC 于点D,CE平分∠ACB,交AD于点G,交AB 于点E,EF⊥BC 于点 F,
求证:四边形AEFG 是菱形.
8.如图,已知点 P 为∠ACB 平分线上的一点,∠ACB=60°,PD⊥CA 于点 D,PE⊥CB 于点E.点 M 是线段 CP上的动点(不与两端点 C,P重合),连接DM,EM.
(1)求证:DM=EM;
(2)当点 M 运动到线段 CP 的什么位置时,四边形 PDME 为菱形,请说明理由.
9.如图,在 ABCD 中,对角线AC,BD交于点O,点E,F在BD上,且BE=DF,连接AE并延长,交BC于点 G,连接CF并延长,交AD 于点 H.
(1)求证:△AOE≌△COF;
(2)若AC 平分∠HAG,求证:四边形 AGCH 是菱形.
第5课时 正方形的性质
1.一个正方形和两个等边三角形的位置如图所示,则∠1 + ∠2+∠3 的度数为 ( )
A.150° B.120°
C.90° D.180°
2.如图,在平面直角坐标系xOy中,正方形ABCD的顶点 D 在 y 轴上,A( -3,0),B(1,b),则正方形ABCD的面积为( )
A.34 B.25 C.20 D.16
3.如图,AC 是正方形ABCD 的对角线,∠DCA 的平分线交 BA 的延长线于点 E,若AB=3,则AE= .
4.如图,将正方形 OABC 放在平面直角坐标系中,O 是原点,A 的坐标为(1, ),则点 C 的坐标为 .
5.如图,在正方形AFCE 中,D 是边CE 上一点,B是 CF 延长线上一点,且 AB =AD,若四边形ABCD的面积是24,则AC 长是 .
6.已知:如图,E 为正方形 ABCD的边BC 延长线上的点,F 是 CD 边上一点,且CE =CF,连接DE,BF,求证:DE=BF.
7.如图,在正方形ABCD中,E,F 分别是边 CD,DA 上的点,且CE =DF,AE 与BF 交于点 M.求证:AE⊥BF.
8.已知:如图,在正方形ABCD 中,点 E 为边 AB的中点,连接DE,点F 在DE上,CF=CD,过点F 作FG⊥FC 交AD于点 G.
(1)求证:GF=GD;
(2)连接AF,求证:AF⊥DE.
C
9.在正方形ABCD中,点 P 是边BC上一动点(不包含端点),线段AP 的垂直平分线与AB,AP,BD,CD分别交于点M,E,F,N.
(1)如图(1),若 PB =a,AB =3a,求线段 MN的长度;
(2)用等式表示 ME,EF,NF 之间的数量关系并证明.
第6课时 正方形的判定
1.在四边形ABCD中,∠A =∠B =∠C=90°,如果再添加一个条件,即可推出该四边形是正方形,这个条件可以是 ( )
A. BC=CD B. AB=CD
C.∠D=90° D. AD=BC
2.有下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD.从中选取两个作为补充条件,使 ABCD 为正方形(如图).现有下列四种选法,其中错误的是 ( )
A.②③
B.②④
C.①②
D.①③
3.在矩形ABCD 中,再增加条件 (只需填一个)可使矩形ABCD 成为正方形.
4.如果一个四边形的两条对角线互相平分,互相垂直且相等,那么这个四边形是 .
5.如图,以△ABC 的三边为边分别作等边△ACD,△ABE,△BCF,则下列结 论: ① △EBF ≌△DFC; ② 四 边 形AEFD 为平行四边形;③当AB = AC,∠BAC =120°时,四边形 AEFD是正方形.其中正确的结论是 .(请写出正确结论的序号).
6.如图,在平面直角坐标系中,四边形ABCD 的顶点坐标分别是A( -2,0),B(0,-2),C(2,0),D(0,2),求证:四边形 ABCD是正方形.
7.如图,在 ABCD 中,对角线AC,BD交于点O,E 是 BD 延长线上的点,且△ACE是等边三角形.
(1)求证:四边形 ABCD 是菱形;
(2)若∠AED=2∠EAD,求证:四边形ABCD 是正方形.
8.如图,菱形 ABCD 的对角线 AC,BD 相交于点O,分别延长OA,OC 到点 E,F,使AE=CF,依次连接B,F,D,E各点.
(1)求证:△BAE≌△BCF;
(2)若∠ABC =40°,则当∠EBA = °时,四边形BFDE 是正方形.
9. 如图,AD 是△ABC 的角平分线,线段 AD 的垂直平分线分别交AB和AC 于点E,F,连接DE,DF.
(1)试判定四边形 AEDF 的形状,并证明你的结论;
(2)若DE =13,EF=10,求AD 的长;
(3)△ABC满足什么条件时,四边形 AEDF 是正方形
第十八章 平行四边形
18.1平行四边形
第 1 课时 平行四边形的性质
1. C 2. C 3.70° 4.5 5. 3
6.证明:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD.
∵E,F分别是OC,OA的中点,
又∠BOE=∠DOF,∴△BOE≌△DOF.
∴BE=DF.
7.解:(1)∵在□ABCD中,∠ABC=50°,∴∠ADC=∠ABC=50°.
∵DF平分∠ADC,∴∠FDC= ∠ADC=25°.
(2)四边形ABCD是平行四边形,
∴AE∥BC.∴∠AEB=∠CBE.
∵BE平分∠ABC,∴∠ABE=∠CBE.
∴∠ABE=∠AEB.∴AE=AB=5.
∵DE=3,∴AD=AE+DE=8.
∴□ABCD的周长=2(AB+AD)=2(5+8)=26.
8.(1)证明:∵四边形ABCD为平行四边形,∴AB∥CD.
∴∠ABC+∠BCD=180°.
∵∠B,∠C的平分线交于点P,
∴∠BPC=90°,即△BPC为直角三角形.
(2)解:∵四边形ABCD为平行四边形,∴AD∥CB.
∴∠CBE=∠BEA,∠BCF=∠CFD.
∴∠ABE=∠BEA,∠DCF=∠CFD.
∴AB=AE=3,CD=DF=3.
∴EF=10.
在 Rt△PEF中,PE=8,EF=10,∴PF=6.
∴△PEF的面积是 24.
9.(1)证明:∵四边形ABCD为平行四边形,
∴AB=CD,AD∥BC.∴∠F=∠DAF.
又∵AF平分∠BAD,∴∠BAE=∠DAF.
∴∠F=∠BAE.
∴AB=BF.∴BF=CD.
(2)解:∵AB=BF,∠F=60°,
∴△ABF 为等边三角形.
∵BE⊥AF,∠F=60°,
∴∠BEF=90°,∠EBF=30°.
在 Rt△BEF中,设EF=x,则 FB=2x.
∴x=2.∴AB=BF=4.
第2 课时 平行四边形的判定
1. B 2. D 3.三 4.(5,3)或(1,-3) 5. 或
6.证明:∵DE=BF,OB=OD,
∴DE-OD=BF-OB.即OE=OF.
又∵OA=OC,∴四边形AECF是平行四边形.
7.证明:∵AB=5,AC=4,BC=3,
∴AB =AC +BC .∴∠BCA=90°.
∵AD∥BC,∴∠DAC=∠BCA=90°.
∵DC=5,AC=4,∴AD =DC -AC =9.
∴AD=BC=3.
∴四边形 ABCD 为平行四边形.
8.证明:(1)∵△BAE是等边三角形,EF⊥AB,
∴∠AEF= ∠AEB=30°,AE=AB,∠EFA=90°.
∵∠ACB=90°,∠BAC=30°,
∴∠AEF=∠BAC,∠EFA=∠ACB.
在△AEF 和△BAC中,
∴△AEF≌△BAC.∴AC=EF.
(2)∵△ACD是等边三角形,
∴AC=AD,∠DAC=60°.
由(1)的结论,得AC=EF.∴AD=EF.
∵∠BAC=30°,
∴∠FAD=∠BAC+∠DAC=90°.
∵∠EFA=90°,∴AD∥EF.
∵AD=EF,
∴四边形ADFE是平行四边形.
9.解:(1)第一次相遇时间 (秒).
(2)当点 M在线段AB 上,点 N 在AC 上时,点 D 在BC上,
∵四边形ANDM为平行四边形,
DM=AN,DM∥AN,
∵△ABC为等边三角形,△BMD和△NCD是等边三角形,
∴BM+CN=CN+AN=10.
此时
当点 M在线段AC 上,点 N 在AB 上时,同理△BND和△MCD是等边三角形.
AM=4t-10,AN=3t-10,
∴AM+AN=AC=10,4t-10+3t-10=10, 此时
当点 M在线段 BC 上,点 N在 AB 上时,点 D 在 AC上,同理△AND和△MCD是等边三角形,CM=4t-20,AN=3t-10,
∴CM=AN.
∴4t-20=3t-10,t=10,不合题意.
综上所述,当 时,点 D 在 BC 上, 当t= 时,点 D在BC上,
第 3 课时 三角形的中位线
1. D 2. A 3.4 4.2 5.1.25
6.解:如图,延长CD交AB于点F,
∵AD平分∠BAC,
∴∠CAD=∠FAD.
∵AD⊥CD,
∴∠ADC=∠ADF=90°.
在△ACD和△AFD中,
∴△ACD≌△AFD.
∴CD=DF,AF=AC=5cm.
∵E为BC 中点,BF=AB-AF=8-5=3,
7.证明:如图,连接 DE,FG,∵BD,CE 是△ABC 的中线,
∴D,E 是 AC,AB 的中点.
∴DE∥BC,
同理:FG∥BC,
∴DE∥FG,DE=FG.
∴四边形 DEFG 是平行四边形.
∴EF∥DG,EF=DG.
解:如图,连接BD,取 BD 的中点M,连接EM 并延长交 BC 于点 N,连接 FM,
∵∠BAD+∠ADC=270°,∴∠ABC+∠C=90°.
∵E,F,M分别是AD,BC,BD的中点,
∴∠MNF=∠ABC,∠MFN=∠C.
∴∠MNF+∠MFN=90°,即∠NMF=90°.
由勾股定理,得ME +MF =EF =16.
9.证明:如图,取 CD 的中点G,连接 EG,FG.
∵E,F 分别是 AD, BC 的中点,
∴∠OMN=∠GEF,∠ONM=∠GFE.
∵OM=ON,∴∠OMN=∠ONM.
∴∠GEF=∠GFE.∴EG=FG.
∴AC=BD.
18.2 特殊的平行四边形
第 1 课时 矩形的性质
1. D 2. C 3.50 4. D 5.
6.(1)证明:∵四边形 ABCD是矩形,∴OB=OD=OC=OA.
∵点 E,F分别是AO,DO的中点,
∵∠BOE=∠COF,∴△BOE≌△COF.
∴BE=CF.
(2)解:∵点E,F分别是AO,DO的中点,∴AD=2EF=6.
∵∠AOD=120°,AO=OD,
∴∠ODA=30°.
在 Rt△ADB中,设 AB=x,则 BD=2x,由 (2x) ,得.
∴矩形的周长为
7.证明:连接AC,如图.
∵CF=AF,
∴∠FCA=∠CAF.
∵四边形 ABCD 是矩形,
∴DC∥AB.
∴∠DCA=∠CAF.
∴∠FCA=∠DCA.
∵AE⊥FC,
∴∠CEA=90°.
∴∠CDA=∠CEA=90°.
在△ADC和△AEC 中,
∴△ADC≌△AEC(AAS).
∴AD=AE.
8.(1)证明:∵四边形ABCD 是矩形,
∴OA=OC=OB=OD,AC=BD,∠ABC=90°.
∵BE=DF,∴OE=OF.
在△AOE 和△COF中,
∴△AOE≌△COF(SAS).∴AE=CF.
(2)解:∵OA=OC,OB=OD,AC=BD,∴OA=OB.
∵∠AOB=∠COD=60°,∴△AOB是等边三角形.
∴OA=AB=3.∴AC=2OA=6.
在 Rt△ABC中,
∴矩形ABCD的面积=
9.解:(1)设ts时两点相遇,根据题意,得t+2t=2(4+8).解得 t=8.
答:经过8 s两点相遇.
答:经过8s两点相遇M不可能在AB 或DC卡.
①如图(1),点 M在E 点右侧时,当AN=ME 时,四边形 AEMN为平行四边形,得8-t=9-2t.解得 t=1.
∵t=1时,点 M 还在 DC 上,
∴t=1 舍去.
②如图(2),点 M在E 点左侧时,当AN=ME时,四边形 ANEM 为平行四边形,得8-t=2t-9.
解得
∴经过 s,点 A,E,M,N 组成平行四边形.
第 2 课时 矩形的判定
1. C 2. B 3.合格 4.∠A=90°(答案不唯一)
5. AD=BC(或AB∥CD,答案不唯一)
6.证明:(1)∵E是AC中点,∴
又∵DB∥EC,
∴四边形 DBCE 是平行四边形.
∴BC=DE.
(2)如图,
∵DB∥AE,DB=AE,
∴四边形 DBEA 是平行四边形.
∵∠BAC=∠C,
∴BA=BC.
∵BC=DE,∴AB=DE.
∴□DBEA是矩形.
7.证明:∵∠AEF,∠CFE的平分线交于点G,
∵AB∥CD,∴∠AEF+∠CFE=180°.
∴∠G=90°.
同理可得∠H=90°.
∵EG,EH分别是∠AEF,∠BEF的平分线,
∴四边形 EGFH 是矩形.
8.解:(1)由题意得 AP=t,BQ=24-3t.
要使四边形ABQP 为矩形,只需 AP=BQ,由t=24-3t,解得t=6.
∴当t=6时,四边形ABQP 成为矩形.
(2)设Q点运动的速度为x cm/s,当运动时间为 ts时,四边形 ABQP 是矩形时其长宽之比为2:1.
∵四边形 APQB是矩形且其长宽之比为2: 1,AB=8cm ,
∴PA=BQ=4 cm或PA=BQ=16 cm.
∴t=24-tx=4或t=24-tx=16.
解得x=5或
∴要使四边形APQB 是矩形时其长宽之比为 2:1,Q点运动的速度为5cm/s或
(1)证明:在□ABCD中,∵AD∥BC,AD=BC,∴∠EBC=∠ADF.由题意知,BE=DF,
在△BEC与△DFA中.
∴△BEC≌△DFA(SAS).
∴CE=AF.同理可得:AE=CF.
∴四边形 AECF 为平行四边形.
(2)解:当t=2或t=10时,四边形AECF为矩形.理由如下:如图,由矩形的性质知,OE=OF,OA=OC,要使∠EAF 是直角,只需
则∠1=∠2,∠3=∠4.
∵∠1+∠2+∠3+∠4=180°,
∴2∠2+2∠3=180°.
∴∠2+∠3=90°,即∠EAF=90°.
此时 或BE=DF=12-2=10cm.
第3 课时 菱形的性质
1. B 2. A 3.2 4.16 5.3
6.证明:∵四边形ABCD是菱形,
∴AB=BC,AD∥BC.∴∠A=∠CBF.
在△ABE 和△BCF 中
∴△ABE≌△BCF(SAS).
∴BE=CF.
7.解:∵四边形ABCD是菱形,∴AB∥CD,AC⊥BD.
∴AE∥CD,∠AOB=90°.
∵DE⊥BD,即∠EDB=90°,∴∠AOB=∠EDB.
∴DE∥AC.
∴四边形 ACDE 是平行四边形.
∵四边形 ABCD是菱形,AC=8,BD=6,
∴AO=4,DO=3,AD=CD=5.
∵四边形 ACDE是平行四边形,∴AE=CD=5.
∴BE=AE+AB=10.
8.(1)证明:∵四边形ABCD是菱形,∴AB=BC.
∵∠ABC=60°,∴△ABC是等边三角形.
∴∠BCA=60°.
∵E 是线段AC 的中点,
∴∠CBE=∠ABE=30°,AE=CE.
∵CF=AE,∴CE=CF.
∴∠CBE=∠F=30°.
∴BE=EF.
(2)解:结论成立.
理由如下:过点 E作EG∥BC交AB 于点G,如图.
∵四边形 ABCD 为菱形,∠ABC=60°,
∴AB=BC,∠BCD=120°,AB∥CD.
∴∠ACD=60°,∠DCF=∠ABC=60°.
∴∠ECF=120°.
又∵∠ABC=60°,∴△ABC是等边三角形.
∴AB=AC,∠ACB=60°.
又∵EG∥BC,∴∠AGE=∠ABC=60°.
又∵∠BAC=60°,∴△AGE是等边三角形.
∴AG=AE=GE,∠AGE=60°.
∴BG=CE,∠BGE=120°=∠ECF.
又∵CF=AE,∴GE=CF.
在△BGE和△ECF中,
∴△BGE≌△ECF(SAS).
∴BE=EF.
9.(1)证明:∵四边形ABCD是菱形,∴CD=CB,∠ACD=∠ACB.
在△DCE 和△BCE 中,
∴△DCE≌△BCE(SAS).
(2)证明:∵△DCE≌△BCE,∴∠CDE=∠CBE.
∵CD∥AB,∴∠CDE=∠F.
∴∠F=∠EBC.
(3)解:∵∠EBF为钝角,∴只能是 BE=BF.
设∠BEF=∠BFE=x°,
可通过三角形内角和为180°,得90+x+x+x=180,解得x=30.
∴∠EFB=30°.
第 4 课时 菱形的判定
1. C 2. D 3.8 4. AB∥CD(答案不唯一) 5.
6.证明:(1)∵△ABC≌△ABD,∴∠ABC=∠ABD.
∵CE∥BD,∴∠CEB=∠DBE.
∴∠CEB=∠CBE.
(2)∵△ABC≌△ABD,∴BC=BD.
∵∠CEB=∠CBE,∴CE=CB.
∴CE=BD.
∵CE∥BD,
∴四边形 BCED 是平行四边形.
∵BC=BD,
∴四边形 BCED 是菱形.
7.证明:∵AD⊥BC,∴∠ADB=90°.
∴∠B+∠BAD=90°.
∵∠BAC=90°,∴∠BAD+∠CAD=90°.
∴∠B=∠CAD.
∵CE平分∠ACB,EF⊥BC,∠BAC=90°(EA⊥CA),
∴AE=EF(角平分线上的点到角两边的距离相等).
∵CE=CE,∴由勾股定理,得AC=CF.
∵△ACG和△FCG中
∴△ACG≌△FCG.∴∠CAD=∠CFG.
∵∠B=∠CAD,∴∠B=∠CFG.
∴GF∥AB.
∵AD⊥BC,EF⊥BC,∴AD∥EF.
∴AG∥EF,AE∥GF.
∴四边形 AEFG 是平行四边形.
∵AE=EF,
∴平行四边形 AEFG是菱形.
8.(1)证明:∵点 P为∠ACB平分线上的一点,
∴∠ACP=∠BCP=30°.
∵PD⊥CA 于点 D,PE⊥CB于点E,
∴PD=PE.
在 Rt△DCP 和Rt△ECP 中,
∴Rt△DCP≌Rt△ECP.∴CD=CE.
在△DCM和△ECM 中.
∴△DCM≌△ECM.∴DM=EM.
(2)解:当点 M 运动到线段 CP 的中点时,四边形PDME为菱形.
理由如下:∵∠DCP=30°,
∴PC=2PD,∠CPD=60°.
∵PD=PE,MD=ME,
∴当 DM=DP 时,PD=PE=MD=ME,则四边形DMEP 为菱形.
此时△PDM为等边三角形,∴PD=PM.
∴CM=PM.
∴当点 M运动到线段CP 的中点时,四边形 PDME为菱形.
9.证明:(1)∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵BE=DF,∴OE=OF.在△AOE 与△COF 中. ∴△AOE≌△COF(SAS).
(2)由(1),得△AOE≌△COF.
∴∠OAE=∠OCF.∴AE∥CF.
∵AH∥CG,
∴四边形 AGCH是平行四边形.
∵AC平分∠HAG,∴∠HAC=∠GAC.
∵AH∥CG,∴∠HAC=∠GCA.
∴∠GAC=∠GCA.∴CG=AG.
∴四边形 AGCH是菱形.
第 5 课时 正方形的性质
1. A 2. B 3.3 4.(- ,1). 5.4
6.证明:∵四边形ABCD 是正方形,
∴BC=DC,∠BCD=90°.
∵E为BC 延长线上的点,∴∠DCE=90°.
∴∠BCD=∠DCE.
在△BCF和△DCE中.
∴△BCF≌△DCE(SAS).
∴DE=BF.
7.证明:∵四边形ABCD 是正方形,
∴AD=CD=AB,∠D=∠BAD=90°.
∵DF=CE,
∴AD-DF=CD-CE,即 AF=DE.
在△ABF 和△DAE中,
∴△ABF≌△DAE.∴∠DAE=∠ABF.
∴∠AMF=∠ABF+∠BAE
=∠DAE+∠BAE=∠BAD=90°.
∴AE⊥BF.
8.证明:(1)∵四边形ABCD是正方形,
∴∠ADC=90°.
∵FG⊥FC,∴∠GFC=90°.
∵CF=CD,∴∠CDF=∠CFD.
∴∠GFC-∠CFD=∠ADC-∠CDF,即∠GFD=∠GDF.
∴GF=GD.
(2)连接CG.
∵CF=CD,GF=GD,
∴点G,C 在线段 FD 的中垂线上.
∴GC⊥DE,∴∠CDF+∠DCG=90°.
∵∠CDF+∠ADE=90°,
∴∠DCG=∠ADE.
∵四边形 ABCD是正方形,
∴AD=DC,∠DAE=∠CDG=90°.
∴△DAE≌△CDG.
∴AE=DG.
∵点E是边AB 的中点,
∴点 G 是边 AD 的中点.
∴AG=GD=GF.
∴∠DAF=∠AFG,∠GDF=∠GFD.
∵∠DAF+∠AFG+∠GFD+∠GDF=180°,
∴2∠AFG+2∠GFD=180°.
∴∠AFD=90°,即AF⊥DE.
9.解:(1)如图(1),过 N作 NG⊥AB,交 AB于点G.
易得四边形 AGND是矩形,∴NG=AD=AB=3a.
∵MN⊥AP,∴∠MNG=∠PAB.
又∠PBA=∠NGM,AB=NG,
∴△ABP≌△NGM.
(2)如图(2),过 P 作 PH∥AB交 MN 于点 H,过 F 作ST∥AB交BC,AD于点S,T,连接AF,PF.
∵NM垂直平分AP,∴AE=PE,∠AEM=∠PEH=90°.
∵PH∥AB,∴∠PHE=∠MEA,∠HPE=∠MAE.
∴△AME≌△PHE.∴ME=HE.
∵∠TDF=∠FBP=45°,∴TD=TF,FS=BS.
∴BS=AT=FS.
∵点 F 在线段AP 的垂直平分线上,∴FP=FA.
∴Rt△FPS≌Rt△ATF.
∴PS=TF=TD=SC.
∵PH∥TS∥CD,∴HF=FN.
∴ME+NF=EF.
第6 课时正方形的判定
1. A 2. C 3. AB=BC(答案不唯一)
4.正方形 5.①②
6.解:∵四边形ABCD的顶点坐标分别是A(--2,0),B(0,-2),C(2,0),D(0,2),
∴OA=OB=OC=OD=2,
即OA=OC,OB=OD 且AC=BD=4.
又∵AC⊥BD,
∴四边形 ABCD是正方形.
7.证明:(1)∵□ABCD,∴AO=OC.
∵△ACE 是等边三角形,
∴EO⊥AC(三线合一),即 BD⊥AC.
∴□ABCD是菱形.
(2)∵△ACE是等边三角形,
由(1)知,EO⊥AC,AO=OC,
∴∠EAO=60°,∠AEO=30°.
∵∠AED=2∠EAD,∴∠EAD=15°.
∴∠DAO=∠EAO-∠EAD=45°.
∵□ABCD是菱形,
∴∠BAD=2∠DAO=90°.
∴菱形ABCD是正方形.
8.(1)证明:∵四边形ABCD是菱形,
∴AB=CB.∴∠BAC=∠BCA.
∴180°—∠BAC=180°-∠BCA,
即∠BAE=∠BCF.
在△BAE 和△BCF 中,
∴△BAE≌△BCF(SAS).
(2)25
9.解:(1)四边形 AEDF是菱形.
理由如下:∵AD 平分∠BAC,∴∠1=∠2.
又∵EF⊥AD,∴∠AOE=∠AOF=90°.
∵在△AEO和△AFO中,
∴△AEO≌△AFO(ASA).∴EO=FO.
∵EF垂直平分AD,∴EF,AD相互平分.
∴四边形 AEDF 是平行四边形.又 EF⊥AD,
∴平行四边形AEDF为菱形.
(2)∵四边形 AEDF 是菱形,EF=10,
在 Rt△DOE 中,∵DE=13,
∴AD=2OD=24.
(3)在△ABC 中,当∠BAC=90°时,四边形 AEDF 是正方形.
∵∠BAC=90°,
∴四边形 AEDF 是正方形(有一个角是直角的菱形是正方形).
