第二十章数据的分析检测卷2023—2024学年人教版数学八年级下册
文档属性
| 名称 | 第二十章数据的分析检测卷2023—2024学年人教版数学八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 651.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-04 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二十章数据的分析检测卷
(90 分钟120 分)
一、选择题(本大题10 小题,每小题3分,共30分)
1.数据5,3,2,1,4 的平均数是 ( )
A.2 B.5 C.4 D.3
2.六个学生进行投篮比赛,投进的个数分别为2,3,3,5,10,13,这六个数的中位数是 ( )
A.3 B.4 C.5 D.6
3.10名学生的体重分别是41,48,50,53,49,53,53,51,67(单位:kg),这组数据的众数是 ( )
A.48 B.50 C.53 D.67
4.中学人数相等的甲、乙两班学生参加了同一次数学测验,班平均分和方差分别为 分, 82 分, 分 ,s =190分 .那么成绩较为整齐的是 ( )
A.甲班 B.乙班 C.两班一样整齐 D.无法确定
5.数据按从小到大排列为1,2,4,x,6,9,这组数据的中位数为5,那么这组数据的众数是 ( )
A.4 B.5 C.5.5 D.6
6.已知一组数据3,a,4,5的众数为4,则这组数据的平均数为 ( )
A.3 B.4 C.5 D.6
7.某排球队12名队员的年龄如下表所示:
年龄/岁 18 19 20 21 22
人数/人 1 4 3 2 2
该队队员年龄的众数与中位数分别是 ( )
A.19岁,19岁 B.19岁,20岁 C.20岁,20岁 D.20岁,22岁
8.某校开展“节约每一滴水”活动,为了解开展活动的一个月以来节约用水的情况,从八年级的400名同学中选出20名同学统计了解各自家庭一个月的节水情况,见下表:
节水量/m 0.2 0.25 0.3 0.4 0.5
家庭数/个 2 4 6 7 1
请你估计这400名同学的家庭一个月节约用水的总量大约是 ( )
A.130 m B.135 m C.6.5 m D.260 m
9.小华所在的九年级(1)班共有 50名学生,一次体检测量了全班学生的身高,由此求得该班学生的平均身高是1.65米,而小华的身高是1.66米,下列说法错误的是 ( )
A.1.65 米是该班学生身高的平均水平 B.班上比小华高的学生人数不会超过25 人
C.这组身高数据的中位数不一定是1.65 米 D.这组身高数据的众数不一定是1.65米
10.张老师想对同学们的打字能力进行测试,他将全班同学分成5组.经统计,这5 个小组平均每分钟打字的个数如下:100,80,x,90,90.已知这组数据的众数与平均数相等,那么这组数据的中位数是
( )
A.70 B.80 C.90 D.100
二、填空题(本大题5小题,每小题4分,共20分)
11.数据1,-3,1,0,-1,2的方差是 ;
12.数学老师布置10道选择题作为课堂练习,课代表将全班同学的答题情况绘制成条形统计图.根据此图可知,每位同学答对的题数所组成样本的中位数为 ,众数为 ;
13.8个数的平均数12,4个数的平均数为18,则这12个数的平均数为 .
14.如图是一组数据的折线统计图,这组数据的极差是 ,平均数是 .
15.一组数据的方差是 则这组数据共有 个,平均数是 .
三、解答题(一)(本大题5小题,每小题6分,共30分)
16.某同学参加了学校举行的“五好小公民·红旗飘飘”演讲比赛,7名评委给该同学的打分(单位:分)情况如下表:
评委 评委 1 评委 2 评委 3 评委4 评委5 评委6 评委7
打分 6 8 7 8 5 7 8
(1)直接写出该同学所得分数的众数与中位数;
(2)计算该同学所得分数的平均数.
17.某市举行一次少年书法比赛,各年级组的参赛人数如下表:
年龄组 13岁 14 岁 15岁 16 岁
参赛人数 5 19 12 14
(1)求全体参赛选手年龄的平均数,众数,中位数;
(2)小明说,他所在年龄组的参赛人数占全体参赛人数的28%,你认为小明是哪个年龄组的选手 请说明理由.
18.甲乙两名运动员在相同条件下各射击5次,成绩如图:(实线表示甲,虚线表示乙)
(1)求出两人射击平均环数:甲 、乙 ;
(2)求出两人方差:甲 、乙 ;
(3)根据图示算得结果,你认为 射击稳定性比较高.
19.甲,乙两台编织机纺织一种毛衣,在5天中两台编织机每天出的合格品数如下(单位:件):甲:7,10,8,8,7;乙:8,9,7,9,7.在这5天中,哪台编织机出合格品的波动较小
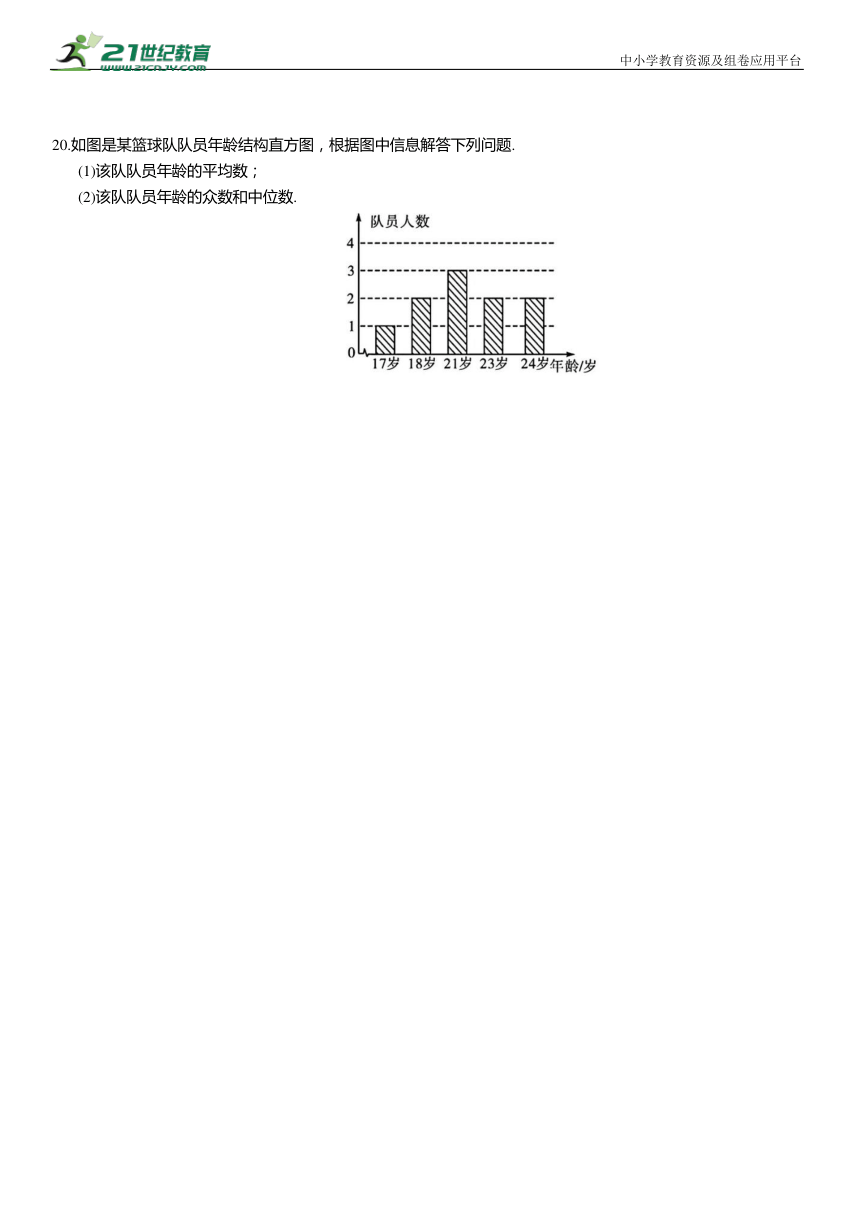
20.如图是某篮球队队员年龄结构直方图,根据图中信息解答下列问题.
(1)该队队员年龄的平均数;
(2)该队队员年龄的众数和中位数.
四、解答题(二)(本大题5小题,每小题8分,共40分)
21.实施素质教育以来,某中学立足于学生的终身发展,大力开发课程资源,在八年级设立六个课外学习小组,下面是八年级学生参加六个学习小组的统计表和扇形统计图,请你根据图表中提供的信息回答下列问题.
学习小组 体育 美术 科技 音乐 写作 奥数
人数 72 36 54 18
(1)八年级共有学生 人;
(2)在表格中的空格处填上相应的数字;
(3)表格中所提供的六个数据的中位数是 ;众数是 .
22.某公司招聘职员,对甲、乙两位候选人进行了面试和笔试,面试中包括形体和口才,笔试中包括专业水平和创新能力考察,他们的成绩(百分制)如下表:
候选人 面试 笔试
形体 口才 专业水平 创新能力
甲 86 90 96 92
乙 92 88 95 93
(1)若公司根据经营性质和岗位要求认为:形体、口才、专业水平、创新能力按照 4:6:5:5的比确定,请计算甲、乙两人各自的平均成绩,看看谁将被录取
(2)若公司根据经营性质和岗位要求认为:面试成绩中形体占15%,口才占20%,笔试成绩中专业水平占40%,创新能力占25%,那么你认为该公司应该录取谁
23.某研究性学习小组为了解本校八年级学生一天中做家庭作业所用的大致时间(时间以整数记,单位:分钟),对本校的八年级学生做了抽样调查,并把调查得到的所有数据(时间)进行整理,分成五个时间段,绘制成统计图(如图所示),请结合统计图中提供的信息,回答下列问题:
(1)这个研究性学习小组所抽取的样本容量是多少
(2)在被调查的学生中,一天做家庭作业所用的大致时间超过120分钟(不包括120分钟)的人数占被调查学生总人数的百分之几
(3)这次调查得到的所有数据的中位数落在了五个时间段中的哪一段内
24.在某市 2018年的一次中学生运动会上,参加男子跳高比赛的有17 名运动员,通讯员在将成绩表送组委会时不慎被墨水污染掉一部分(如下表),但他记得这组运动员的成绩的众数是1.75米,表中每个成绩都至少有一名运动员.根据这些信息,可以计算出这17名运动员的平均跳高成绩是多少米 (精确到0.01 米)
成绩/米 1.50 1.60 1.65 1.70 1.75 1.80 1.85 1.90
人数 2 3 2 3 1 1
25.为积极响应“弘扬传统文化”的号召,某学校倡导全校1200名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根据调查结果绘制成的统计图(部分)如图所示.
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表.
一周诗词诵背数量 3 首 4 首 5首 6首 7首 8首
人数 10 10 15 40 25 20
请根据调查的信息分析:
(1)活动启动之初学生“一周诗词诵背数量”的中位数为 ;
(2)估计大赛后一个月该校学生一周诗词诵背6首(含 6首)以上的人数;
(3)选择适当的统计量,从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.
第二十章检测卷
1. D 2. B 3. C 4. B 5. D 6. B 7. B 8. A 9. B10. C 11. 12.9
13.14 14.31 46.5 15.10 4
16.解:(1)从小到大排列此数据为5,6,7,7,8,8,8.
数据8出现了三次最多为众数,7 处在第 4 位为中位数.
(2)该同学所得分数的平均数为(5+6+7×2+8×3)÷7=7.
17.解:(1)平均数是 14.7 岁; 众数是 14岁;中位数是15 岁.
(2)∵全体参赛选手的人数为 5+19+12+14=50 名.
又∵50×28%=14(名),∴小明是 16 岁年龄组的选手.
18.解:(1)8 8 (2)5.2 0.4 (3)乙
19.解
因为
所以乙纺织机出合格品的波动较小.
20.解:(1)该队队员的平均年龄是 21×3+23×2+24×2)=21(岁).
(2)该队队员年龄的众数为21岁;中位数为21岁.
21.(1)360 (2)72 108 (3)63 72
22.解:(1)甲: (分).
8(分).录取乙.
(2)甲:86×15%+90×20%+96×40%+92×25%=92.3(分).
乙:92×15%+88×20%+95×40%+93×25%=92.65(分).
录取乙.
23.解:(1)30人
(3)120.5~150.5
24.解:根据题意可知,∵已有12人的成绩,∴1.75米和1.80米的共有5人,∵这组运动员的成绩的众数是1.75米,表中每个成绩都至少有一名运动员,∴成绩为1.75的有4人,成绩为1.80的有 1人,所以这 17名运动员的平均跳高成绩=(1.50×2+1.60×3+1.65×2+1.70×3+1.75×4+1.80+1.85+1.90)÷17≈1.69米.
答:1.75米和1.80米的运动员各有4人,1人,这 17名运动员的平均跳高成绩是1.69米.
25.解:(1)本次调查的学生有 (名),背诵4首的有 120-15-20-16-13-11=45(人),
∵15+45=60,
∴这组数据的中位数是(4+5)÷2=4.5(首).
故答案为4.5首.
(2)大赛后一个月该校学生一周诗词诵背6 首(含 6首)以上的有 (人).
答:大赛后一个月该校学生一周诗词诵背6首(含 6首)以上的有850人.
(3)活动启动之初的中位数是4.5 首,众数是4首.大赛比赛后一个月时的中位数是 6首,众数是 6首.由比赛前后的中位数和众数看,比赛后学生背诵诗词的积极性明显提高,这次举办后的效果比较理想.
第二十章数据的分析检测卷
(90 分钟120 分)
一、选择题(本大题10 小题,每小题3分,共30分)
1.数据5,3,2,1,4 的平均数是 ( )
A.2 B.5 C.4 D.3
2.六个学生进行投篮比赛,投进的个数分别为2,3,3,5,10,13,这六个数的中位数是 ( )
A.3 B.4 C.5 D.6
3.10名学生的体重分别是41,48,50,53,49,53,53,51,67(单位:kg),这组数据的众数是 ( )
A.48 B.50 C.53 D.67
4.中学人数相等的甲、乙两班学生参加了同一次数学测验,班平均分和方差分别为 分, 82 分, 分 ,s =190分 .那么成绩较为整齐的是 ( )
A.甲班 B.乙班 C.两班一样整齐 D.无法确定
5.数据按从小到大排列为1,2,4,x,6,9,这组数据的中位数为5,那么这组数据的众数是 ( )
A.4 B.5 C.5.5 D.6
6.已知一组数据3,a,4,5的众数为4,则这组数据的平均数为 ( )
A.3 B.4 C.5 D.6
7.某排球队12名队员的年龄如下表所示:
年龄/岁 18 19 20 21 22
人数/人 1 4 3 2 2
该队队员年龄的众数与中位数分别是 ( )
A.19岁,19岁 B.19岁,20岁 C.20岁,20岁 D.20岁,22岁
8.某校开展“节约每一滴水”活动,为了解开展活动的一个月以来节约用水的情况,从八年级的400名同学中选出20名同学统计了解各自家庭一个月的节水情况,见下表:
节水量/m 0.2 0.25 0.3 0.4 0.5
家庭数/个 2 4 6 7 1
请你估计这400名同学的家庭一个月节约用水的总量大约是 ( )
A.130 m B.135 m C.6.5 m D.260 m
9.小华所在的九年级(1)班共有 50名学生,一次体检测量了全班学生的身高,由此求得该班学生的平均身高是1.65米,而小华的身高是1.66米,下列说法错误的是 ( )
A.1.65 米是该班学生身高的平均水平 B.班上比小华高的学生人数不会超过25 人
C.这组身高数据的中位数不一定是1.65 米 D.这组身高数据的众数不一定是1.65米
10.张老师想对同学们的打字能力进行测试,他将全班同学分成5组.经统计,这5 个小组平均每分钟打字的个数如下:100,80,x,90,90.已知这组数据的众数与平均数相等,那么这组数据的中位数是
( )
A.70 B.80 C.90 D.100
二、填空题(本大题5小题,每小题4分,共20分)
11.数据1,-3,1,0,-1,2的方差是 ;
12.数学老师布置10道选择题作为课堂练习,课代表将全班同学的答题情况绘制成条形统计图.根据此图可知,每位同学答对的题数所组成样本的中位数为 ,众数为 ;
13.8个数的平均数12,4个数的平均数为18,则这12个数的平均数为 .
14.如图是一组数据的折线统计图,这组数据的极差是 ,平均数是 .
15.一组数据的方差是 则这组数据共有 个,平均数是 .
三、解答题(一)(本大题5小题,每小题6分,共30分)
16.某同学参加了学校举行的“五好小公民·红旗飘飘”演讲比赛,7名评委给该同学的打分(单位:分)情况如下表:
评委 评委 1 评委 2 评委 3 评委4 评委5 评委6 评委7
打分 6 8 7 8 5 7 8
(1)直接写出该同学所得分数的众数与中位数;
(2)计算该同学所得分数的平均数.
17.某市举行一次少年书法比赛,各年级组的参赛人数如下表:
年龄组 13岁 14 岁 15岁 16 岁
参赛人数 5 19 12 14
(1)求全体参赛选手年龄的平均数,众数,中位数;
(2)小明说,他所在年龄组的参赛人数占全体参赛人数的28%,你认为小明是哪个年龄组的选手 请说明理由.
18.甲乙两名运动员在相同条件下各射击5次,成绩如图:(实线表示甲,虚线表示乙)
(1)求出两人射击平均环数:甲 、乙 ;
(2)求出两人方差:甲 、乙 ;
(3)根据图示算得结果,你认为 射击稳定性比较高.
19.甲,乙两台编织机纺织一种毛衣,在5天中两台编织机每天出的合格品数如下(单位:件):甲:7,10,8,8,7;乙:8,9,7,9,7.在这5天中,哪台编织机出合格品的波动较小
20.如图是某篮球队队员年龄结构直方图,根据图中信息解答下列问题.
(1)该队队员年龄的平均数;
(2)该队队员年龄的众数和中位数.
四、解答题(二)(本大题5小题,每小题8分,共40分)
21.实施素质教育以来,某中学立足于学生的终身发展,大力开发课程资源,在八年级设立六个课外学习小组,下面是八年级学生参加六个学习小组的统计表和扇形统计图,请你根据图表中提供的信息回答下列问题.
学习小组 体育 美术 科技 音乐 写作 奥数
人数 72 36 54 18
(1)八年级共有学生 人;
(2)在表格中的空格处填上相应的数字;
(3)表格中所提供的六个数据的中位数是 ;众数是 .
22.某公司招聘职员,对甲、乙两位候选人进行了面试和笔试,面试中包括形体和口才,笔试中包括专业水平和创新能力考察,他们的成绩(百分制)如下表:
候选人 面试 笔试
形体 口才 专业水平 创新能力
甲 86 90 96 92
乙 92 88 95 93
(1)若公司根据经营性质和岗位要求认为:形体、口才、专业水平、创新能力按照 4:6:5:5的比确定,请计算甲、乙两人各自的平均成绩,看看谁将被录取
(2)若公司根据经营性质和岗位要求认为:面试成绩中形体占15%,口才占20%,笔试成绩中专业水平占40%,创新能力占25%,那么你认为该公司应该录取谁
23.某研究性学习小组为了解本校八年级学生一天中做家庭作业所用的大致时间(时间以整数记,单位:分钟),对本校的八年级学生做了抽样调查,并把调查得到的所有数据(时间)进行整理,分成五个时间段,绘制成统计图(如图所示),请结合统计图中提供的信息,回答下列问题:
(1)这个研究性学习小组所抽取的样本容量是多少
(2)在被调查的学生中,一天做家庭作业所用的大致时间超过120分钟(不包括120分钟)的人数占被调查学生总人数的百分之几
(3)这次调查得到的所有数据的中位数落在了五个时间段中的哪一段内
24.在某市 2018年的一次中学生运动会上,参加男子跳高比赛的有17 名运动员,通讯员在将成绩表送组委会时不慎被墨水污染掉一部分(如下表),但他记得这组运动员的成绩的众数是1.75米,表中每个成绩都至少有一名运动员.根据这些信息,可以计算出这17名运动员的平均跳高成绩是多少米 (精确到0.01 米)
成绩/米 1.50 1.60 1.65 1.70 1.75 1.80 1.85 1.90
人数 2 3 2 3 1 1
25.为积极响应“弘扬传统文化”的号召,某学校倡导全校1200名学生进行经典诗词诵背活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查“一周诗词诵背数量”,根据调查结果绘制成的统计图(部分)如图所示.
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表.
一周诗词诵背数量 3 首 4 首 5首 6首 7首 8首
人数 10 10 15 40 25 20
请根据调查的信息分析:
(1)活动启动之初学生“一周诗词诵背数量”的中位数为 ;
(2)估计大赛后一个月该校学生一周诗词诵背6首(含 6首)以上的人数;
(3)选择适当的统计量,从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.
第二十章检测卷
1. D 2. B 3. C 4. B 5. D 6. B 7. B 8. A 9. B10. C 11. 12.9
13.14 14.31 46.5 15.10 4
16.解:(1)从小到大排列此数据为5,6,7,7,8,8,8.
数据8出现了三次最多为众数,7 处在第 4 位为中位数.
(2)该同学所得分数的平均数为(5+6+7×2+8×3)÷7=7.
17.解:(1)平均数是 14.7 岁; 众数是 14岁;中位数是15 岁.
(2)∵全体参赛选手的人数为 5+19+12+14=50 名.
又∵50×28%=14(名),∴小明是 16 岁年龄组的选手.
18.解:(1)8 8 (2)5.2 0.4 (3)乙
19.解
因为
所以乙纺织机出合格品的波动较小.
20.解:(1)该队队员的平均年龄是 21×3+23×2+24×2)=21(岁).
(2)该队队员年龄的众数为21岁;中位数为21岁.
21.(1)360 (2)72 108 (3)63 72
22.解:(1)甲: (分).
8(分).录取乙.
(2)甲:86×15%+90×20%+96×40%+92×25%=92.3(分).
乙:92×15%+88×20%+95×40%+93×25%=92.65(分).
录取乙.
23.解:(1)30人
(3)120.5~150.5
24.解:根据题意可知,∵已有12人的成绩,∴1.75米和1.80米的共有5人,∵这组运动员的成绩的众数是1.75米,表中每个成绩都至少有一名运动员,∴成绩为1.75的有4人,成绩为1.80的有 1人,所以这 17名运动员的平均跳高成绩=(1.50×2+1.60×3+1.65×2+1.70×3+1.75×4+1.80+1.85+1.90)÷17≈1.69米.
答:1.75米和1.80米的运动员各有4人,1人,这 17名运动员的平均跳高成绩是1.69米.
25.解:(1)本次调查的学生有 (名),背诵4首的有 120-15-20-16-13-11=45(人),
∵15+45=60,
∴这组数据的中位数是(4+5)÷2=4.5(首).
故答案为4.5首.
(2)大赛后一个月该校学生一周诗词诵背6 首(含 6首)以上的有 (人).
答:大赛后一个月该校学生一周诗词诵背6首(含 6首)以上的有850人.
(3)活动启动之初的中位数是4.5 首,众数是4首.大赛比赛后一个月时的中位数是 6首,众数是 6首.由比赛前后的中位数和众数看,比赛后学生背诵诗词的积极性明显提高,这次举办后的效果比较理想.
