11.1全等三角形的判定
文档属性
| 名称 | 11.1全等三角形的判定 |  | |
| 格式 | rar | ||
| 文件大小 | 288.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-09-03 14:10:00 | ||
图片预览



文档简介
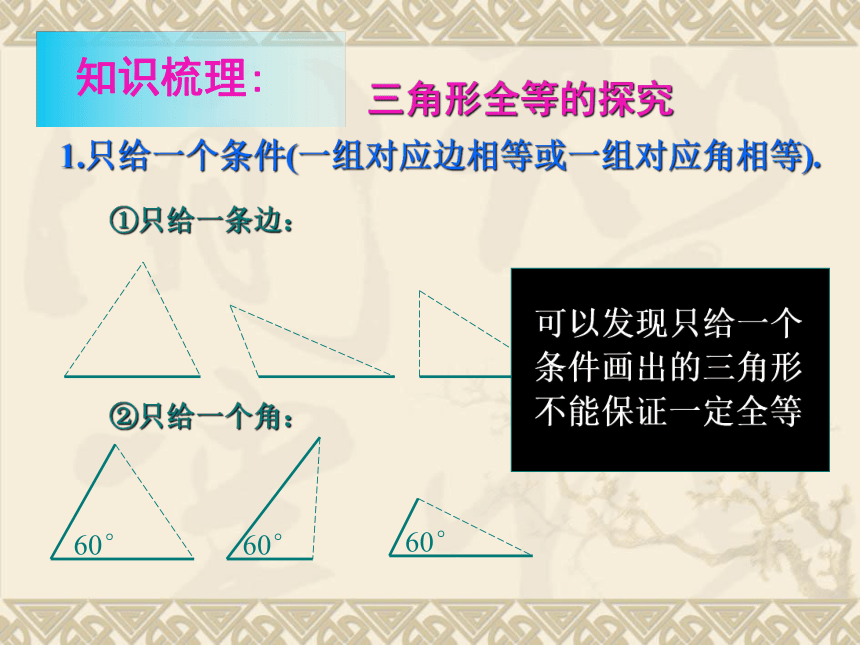
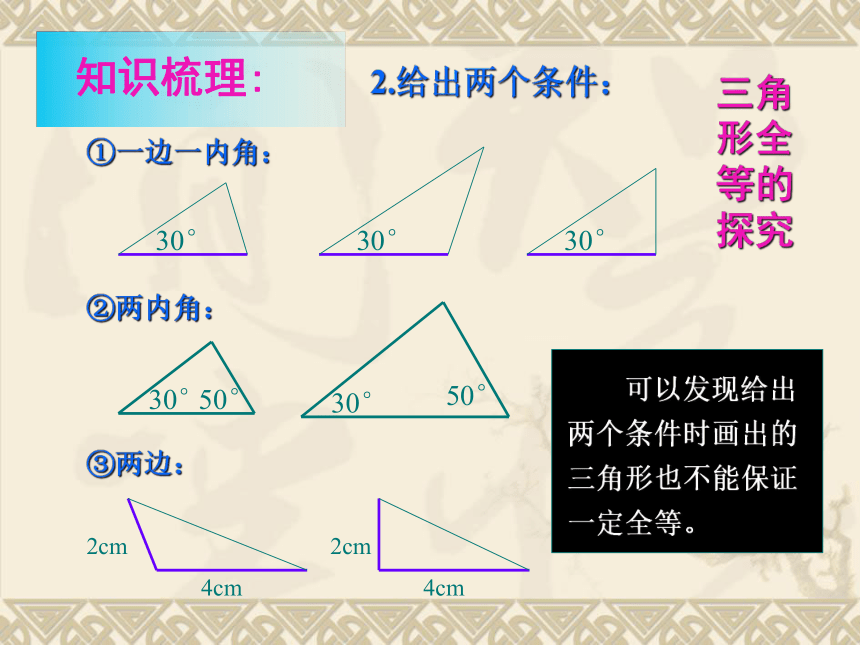
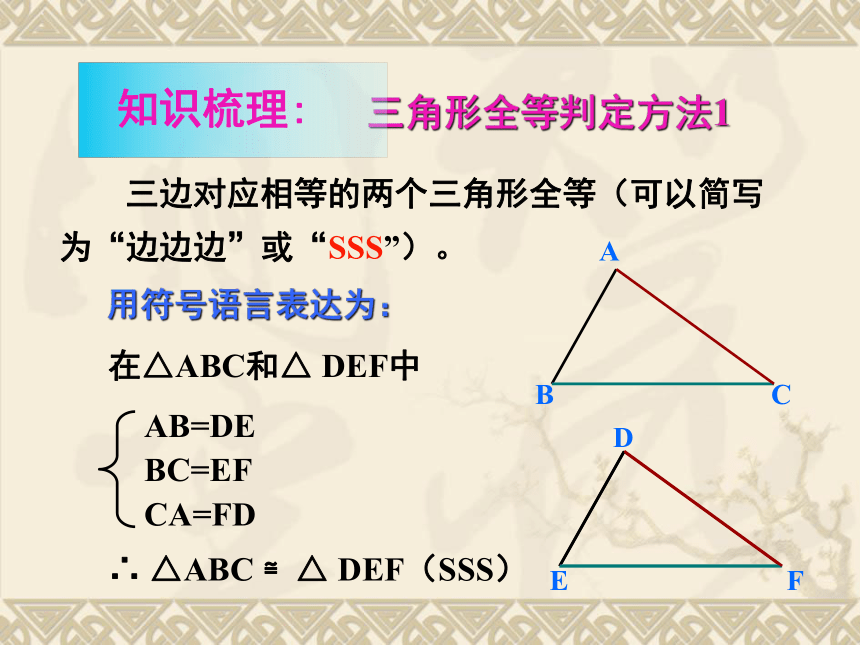
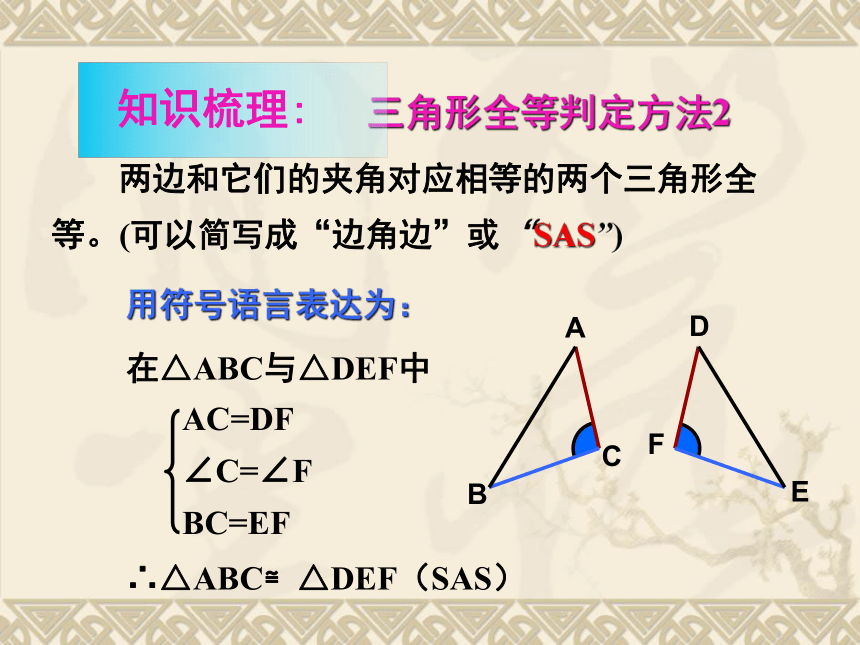
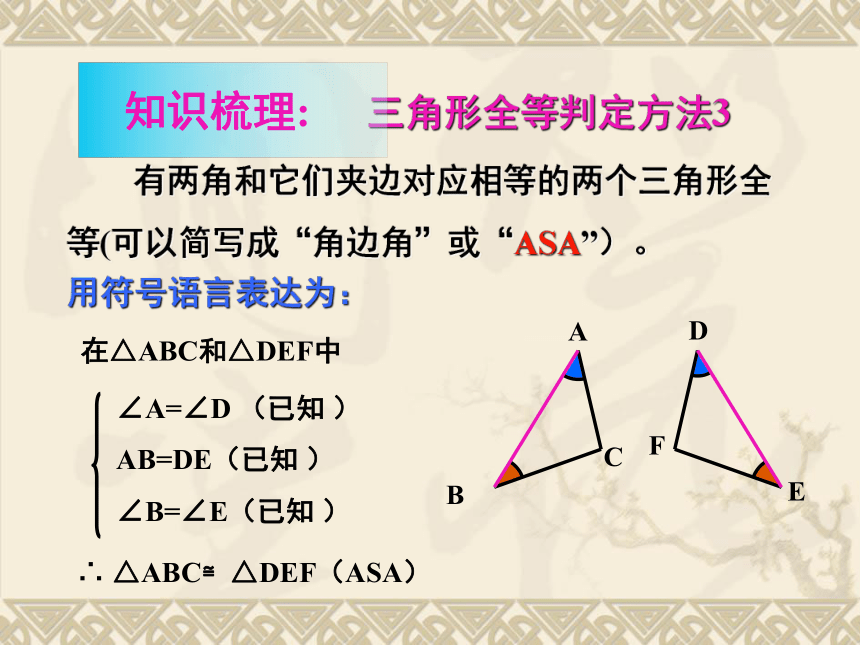
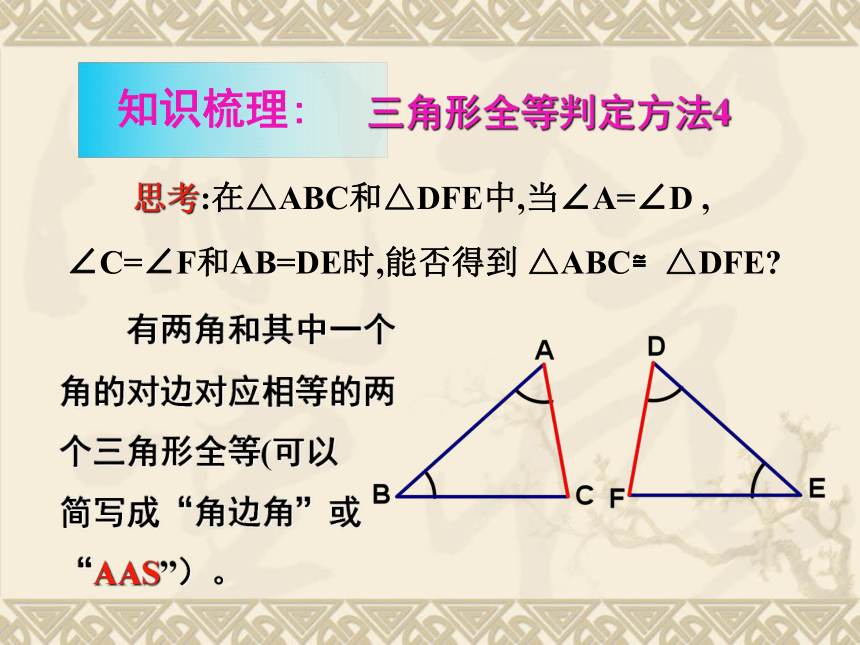
课件24张PPT。11.2全等三角形的判定1.了解判定两个三角形全等的4种方法,并能应用它们解决简单问题;2.学会用全等的方法证明线段(角)的相等;3.初步认识全等的证明思路,学会合理思考.1.学习重点:2.学习难点:运用4个判定方法进行简单的证明;运用判定方法进行合理的思考.1.只给一个条件(一组对应边相等或一组对应角相等).①只给一条边:②只给一个角:可以发现只给一个条件画出的三角形不能保证一定全等 三角形全等的探究2.给出两个条件:①一边一内角:②两内角:③两边: 可以发现给出两个条件时画出的三角形也不能保证一定全等。三角形全等的探究 三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)。在△ABC和△ DEF中∴ △ABC ≌△ DEF(SSS)用符号语言表达为: 三角形全等判定方法1 三角形全等判定方法2用符号语言表达为:在△ABC与△DEF中∴△ABC≌△DEF(SAS) 两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或“SAS”)FEDCBA在△ABC和△DEF中∴ △ABC≌△DEF(ASA) 有两角和它们夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA”)。用符号语言表达为:FEDCBA 三角形全等判定方法3 思考:在△ABC和△DFE中,当∠A=∠D , ∠C=∠F和AB=DE时,能否得到 △ABC≌△DFE? 三角形全等判定方法4 有两角和其中一个角的对边对应相等的两个三角形全等(可以 简写成“角边角”或“AAS”)。ABDABCSSA不能判定全等例1 (2006浙江):如图,点B在AE上,∠CAB=∠DAB,要使ΔABC≌ΔABD,可补充的一个条件是 .分析:现在我们已知 A→∠CAB=∠DAB①用SAS,需要补充条件AB=AC, ②用ASA,需要补充条件∠CBA=∠DBA, ③用AAS,需要补充条件∠C=∠D, ④此外,补充条件∠CBE=∠DBE也可以(?) SASASAAASS→ AB=AB(公共边) .AB=AC ∠CBA=∠DBA∠C=∠D∠CBE=∠DBE例2 (2006湖南株洲):如图,AE=AD,要使ΔABD≌ΔACE,请你增加一个条件是 .分析:现在我们已知 S→ AE=AD①用SAS,需要补充条件AB=AC, ②用ASA,需要补充条件∠ADB=∠AEC, ③用AAS,需要补充条件∠B=∠ C, ④此外,补充条件∠BDC=∠BEC也可以(?) SASASAAAS(CD=BE行吗?)A→∠A=∠A (公共角) .例3 (2006湖北十堰):如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE,②BC=ED,③∠C=∠D,④ ∠B=∠E,其中能使ΔABC≌ΔAED的条件有( )个. A.4 B.3 C.2 D.1∵∠1=∠2 (已知) ∴ ∠1+∠EAB = ∠2+ ∠EAB, 即∠BAC=∠EAD例3 (2006湖北十堰):如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE,②BC=ED,③∠C=∠D,④ ∠B=∠E,其中能使ΔABC≌ΔAED的条件有( )个. A.4 B.3 C.2 D.1在ΔABC和ΔAED中AB=AE∴ΔABC≌ΔAED(SAS)AB=AE①AB=AE例3 (2006湖北十堰):如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE,②BC=ED,③∠C=∠D,④ ∠B=∠E,其中能使ΔABC≌ΔAED的条件有( )个. A.4 B.3 C.2 D.1在ΔABC和ΔAED中AC=AD ∠BAC=∠EADBC=ED∴ΔABC与ΔAED不全等BC=ED例3 (2006湖北十堰):如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE,②BC=ED,③∠C=∠D,④ ∠B=∠E,其中能使ΔABC≌ΔAED的条件有( )个. A.4 B.3 C.2 D.1在ΔABC和ΔAED中∠C=∠D∴ΔABC≌ΔAED(ASA)∠C=∠D③∠C=∠D,例3 (2006湖北十堰):如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE,②BC=ED,③∠C=∠D,④ ∠B=∠E,其中能使ΔABC≌ΔAED的条件有( )个. A.4 B.3 C.2 D.1在ΔABC和ΔAED中∠B=∠E∴ΔABC≌ΔAED(AAS)∠B=∠E∠B=∠E,B例4 (2007金华):如图, A,E,B,D在同一直线上, AB=DE,AC=DF,AC ∥ DF,在ΔABC和ΔDEF, (1)求证: ΔABC≌ΔDEF;(1)证明:∵AC∥DF(已知) ∴∠A=∠D (两直线平行,内错角相等)∴ΔABC≌ΔDEF(SAS)在ΔABC和ΔDEF中例4 (2007金华):如图,A,E,B,D在同一直线上, 在ΔABC和ΔDEF中, AB=DE,AC=DF,AC∥DF, (2)你还可以得到的结论是 .(写出一个,不再添加其他线段,不再表注或使用其他字母)解:根据”全等三角形的对应边(角)相等”可知:②∠C=∠F, ③∠ABC=∠ DEF, ④ EF∥BC,⑤AE=DB等①BC=EF,例5 已知:如图,AB=AD,
AC=AE,∠1=∠2,
求证:∠B=∠D.证明: ∵∠1=∠2 (已知) ∴ ∠1+∠DAC = ∠2+ ∠DAC, 即∠BAC=∠DAE在ΔABC和ΔADE中 AB=AD(已知)
∠BAC=∠DAE(已证)
AC=AE (已知) ∴ ΔABC≌ΔADE(SAS) ∴ ∠B=∠D(全等三角形的对应角相等)例6 (2005年昆明):如图,已知,AB=CD,CE=DF,AE=BF,则AE∥DF吗?为什么?证明: AE∥DF,理由是: ∵AB=CD(已知) ∴ AB+BC=CD+BC, 即AC=BD. ∴ ΔACE≌ΔBDF(SSS)在ΔACE和ΔBDF中AC=BD(已证) CE=DF (已知) AE=BF (已知) ∴∠E=∠F(全等三角形的对应角相等) ∴ AE∥DF(内错角相等,两直线平行)∵BE=EB(公共边)又∵ AC∥ DB(已知) ∠DBE=∠CEB (两直线平行,内错角相等)例7 (2006湖北黄冈):如图, AC∥ DB, AC=2DB,E是AC的中点,求证:BC=DE证明:∵AC=2DB,AE=EC (已知) ∴DB=ECDB=EC∠DBE=∠CEBBE=EB∴ ΔDBE≌ΔCEB(SAS) ∴ BC=DE (全等三角形的对应边相等)例8 (2006年烟台):如图在 ΔABC中,AD⊥BC于D,BE⊥AC于E,AD交BE于F,若BF=AC,那么∠ABC的大小是( )A.40° B.50° C.60° D.45°解: ∵AD⊥BC,BE⊥AC ∴∠ADB=∠ ADC= ∠BEC= 90°∴ ∠1=∠2在ΔACD和ΔBDF中12∠1=∠2(已证) AC= BF(已知) ∠ADC=∠ ADB (已证) ∴ ΔACD≌ΔBDF(ASA) ∴ AD=BD(全等三角形对应边相等)∴ ∠ABC=45 °.选DD小结:1.在证明全等三角形或利用它证明线段或角的相等时,首先要寻找我们已经知道了什么(从已知条件,公共边,公共角,对顶角等隐含条件中找对应相等的边或角),其次要搞清我们还需要什么,而这一步我们就要依照4个判定方法去思考了.2.注意正确地书写证明格式(顺序和对应关系).
AC=AE,∠1=∠2,
求证:∠B=∠D.证明: ∵∠1=∠2 (已知) ∴ ∠1+∠DAC = ∠2+ ∠DAC, 即∠BAC=∠DAE在ΔABC和ΔADE中 AB=AD(已知)
∠BAC=∠DAE(已证)
AC=AE (已知) ∴ ΔABC≌ΔADE(SAS) ∴ ∠B=∠D(全等三角形的对应角相等)例6 (2005年昆明):如图,已知,AB=CD,CE=DF,AE=BF,则AE∥DF吗?为什么?证明: AE∥DF,理由是: ∵AB=CD(已知) ∴ AB+BC=CD+BC, 即AC=BD. ∴ ΔACE≌ΔBDF(SSS)在ΔACE和ΔBDF中AC=BD(已证) CE=DF (已知) AE=BF (已知) ∴∠E=∠F(全等三角形的对应角相等) ∴ AE∥DF(内错角相等,两直线平行)∵BE=EB(公共边)又∵ AC∥ DB(已知) ∠DBE=∠CEB (两直线平行,内错角相等)例7 (2006湖北黄冈):如图, AC∥ DB, AC=2DB,E是AC的中点,求证:BC=DE证明:∵AC=2DB,AE=EC (已知) ∴DB=ECDB=EC∠DBE=∠CEBBE=EB∴ ΔDBE≌ΔCEB(SAS) ∴ BC=DE (全等三角形的对应边相等)例8 (2006年烟台):如图在 ΔABC中,AD⊥BC于D,BE⊥AC于E,AD交BE于F,若BF=AC,那么∠ABC的大小是( )A.40° B.50° C.60° D.45°解: ∵AD⊥BC,BE⊥AC ∴∠ADB=∠ ADC= ∠BEC= 90°∴ ∠1=∠2在ΔACD和ΔBDF中12∠1=∠2(已证) AC= BF(已知) ∠ADC=∠ ADB (已证) ∴ ΔACD≌ΔBDF(ASA) ∴ AD=BD(全等三角形对应边相等)∴ ∠ABC=45 °.选DD小结:1.在证明全等三角形或利用它证明线段或角的相等时,首先要寻找我们已经知道了什么(从已知条件,公共边,公共角,对顶角等隐含条件中找对应相等的边或角),其次要搞清我们还需要什么,而这一步我们就要依照4个判定方法去思考了.2.注意正确地书写证明格式(顺序和对应关系).
