含有绝对值的不等式的解法

课件23张PPT。不等式的解法和证明 两个数的差的绝对值表示数轴上这两个
个数对应的两点间距离.复习：1.绝对值的定义:2.几何意义:AB|x2-x1|=OA=AB 一个数的绝对值表示数轴上这个数对
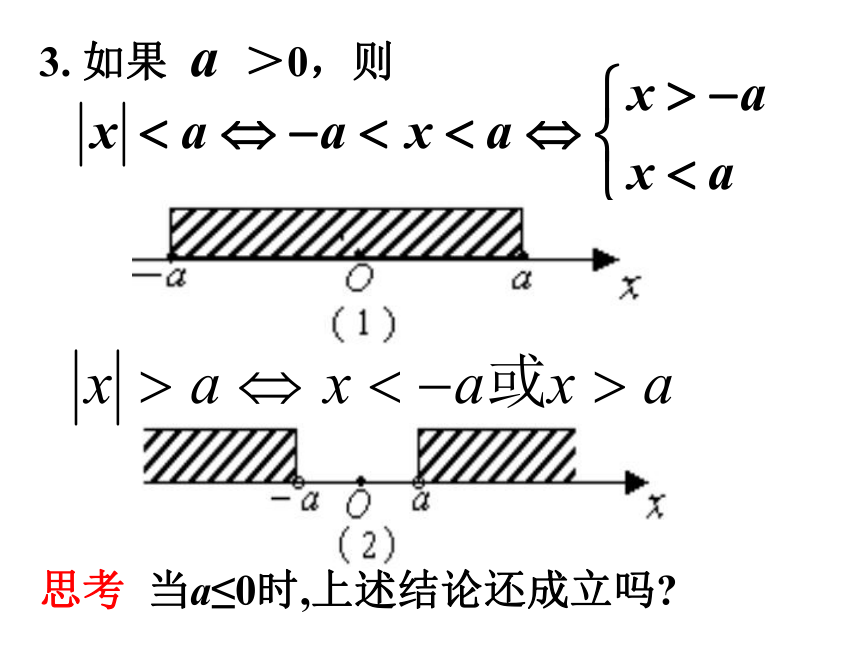
应的点到原点的距离.|x2|=OBx1x2|x1|3. 如果 a ＞0，则 思考 当a≤0时,上述结论还成立吗?解题反思：整体换元。例1 解不等式 (1) |3x-1|≤6
(2) |2-x|>3归纳：形如| f(x)|a 不等式的解法:变1　解不等式 | 5x-6 | < 6 – x分析：对绝对值里面的代数式符号讨论(Ⅰ)或 　　　　 (Ⅱ) 解(Ⅰ)得：6/5≤x<2解(Ⅱ) 得：00
所以0 0x <2即∴∴ 0< x <2总结:
|f(x)||f(x)|>g(x) f(x)>g(x) 或f(x)<-g(x) 3.型如|ax+b|+|cx+d|≥k(≤k)(k∈R)不等式解法例 解不等式|x-1|+|x+2|≥5方法一：利用绝对值的几何意义，体现了数型结合的思想．解:|x-1|+|x+2|=5的解为x=-3或x=2所以原不等式的解为零点划分法解：１０当x>1时，原不等式同解于X≥2X≤-3综合上述知不等式的解为例 解不等式|x-1|+|x+2|≥53０当x<-2时，原不等式同解于2０当-2≤x≤1时，原不等式同解于方法二：利用|x-1|=0，|x+2|=0的解体，将数轴分为三个区间，然后在这三个区间上将原不等式化为不含绝对值符号的不等式求解．现了分类讨论的思想．例 解不等式|x-1|+|x+2|≥5(x-1)+(x+2)-5 x>1-(x-1)+(x+2)-5 -2≤x≤1-(x-1)-(x+2)-5 x<-2解 原不等式化为|x-1|+|x+2|-5 ≥0令f(x)=|x-1|+|x+2|-5 ,则由图象知不等式
的解为方法三：通过构造函数，利用了函数的图象，体现了函数与方程的思想．问题:解不等式|2x-4|-|3x+9|<1解：１０当x>2时，原不等式同解于X>23０当x<-3时，原不等式同解于2０当-3≤x≤2时，原不等式同解于X<-13综合上述知不等式的解为变1 解不等式|2x+1|-|x-2|>0x<-3,或x>1/3４. 常用性质:问题1 |a+b|=|a|+|b| 吗? |a-b|=|a|-|b|吗?问题2 |a+b| 与 |a|+|b| 的大小有何关系呢? 探究1 通过代入具体数字作比较 , 归纳
得出: |a+b|≤|a|+|b| 性质1 如果a, b是实数，则
|a| +|b| ≥|a+b| ，
当且仅当ab≥0时，等号成立。绝对值三角不等式定理1 (绝对值三角不等式) ------如果a、b是实数,则|a+b|≤|a|+|b| ------当且仅当ab≥0时,等号成立证明(1)当ab≥0时, (2) 当ab<0时, 综合(1),(2)知定理成立.定理1 (绝对值三角不等式) ------如果a、b是实数,则|a+b|≤|a|+|b| ------当且仅当ab≥0时,等号成立定理 如果a、b是实数, -------- 那么||a|-|b||≤|a+b|≤|a|+|b| 当且仅当ab ≤0时,
等号成立.当且仅当ab ≥0时,
等号成立.定理 如果a、b是实数, ---------那么||a|-|b||≤|a-b|≤|a|+|b| 当且仅当ab ≤0时,
等号成立.当且仅当ab ≥0时,
等号成立. 如果a,b,c是实数,那么
当且仅当(a-c)(b-c) ≤0时,等号成立证例４ 两个施工队分别被安排在公路沿线的两个地点施工,这两个地点分别位于公路路碑的第10公里和第20公里处.现要在公路沿线建两个施工队的共同临时生活区,每个施工队每天在生活区和施工地点之间往返一次,要使两个施工队每天往返的路程之和最小,生活区应该建于何处?解：如果生活区建于公路路碑的第 x km处，两施工队每天往返的路程之和为S(x)km那么 S(x)=2(|x-10|+|x-20|)答: 生活区建于两路碑间的任意位置都满足条件.课堂小结
含绝对值的不等式的解法的基本思想是去掉绝对值符号.
常用方法 (1)定义法(常用零点划分法)；
(2)公式法 ； (3)平方法； (4)换元法;
(5)数形结合法绝对值的几何意义函数法练习:P19 　　　　　　　　
３４５８