不等式证明
图片预览






文档简介
课件17张PPT。 第二讲 证明不等式的基本方法
分析法引例
证明:1、作差法:作差——变形——定符号
2、分析法的特点是:执果索因. 分析时贵在变形,不通思变,变则通! 用分析法证明不等式的模式是:
要证B成立
只要证 成立
只要证 成立
只要A成立
今已知A成立
故B得证.例1.求证:注:对于思路不明显,感到无从下手的问题
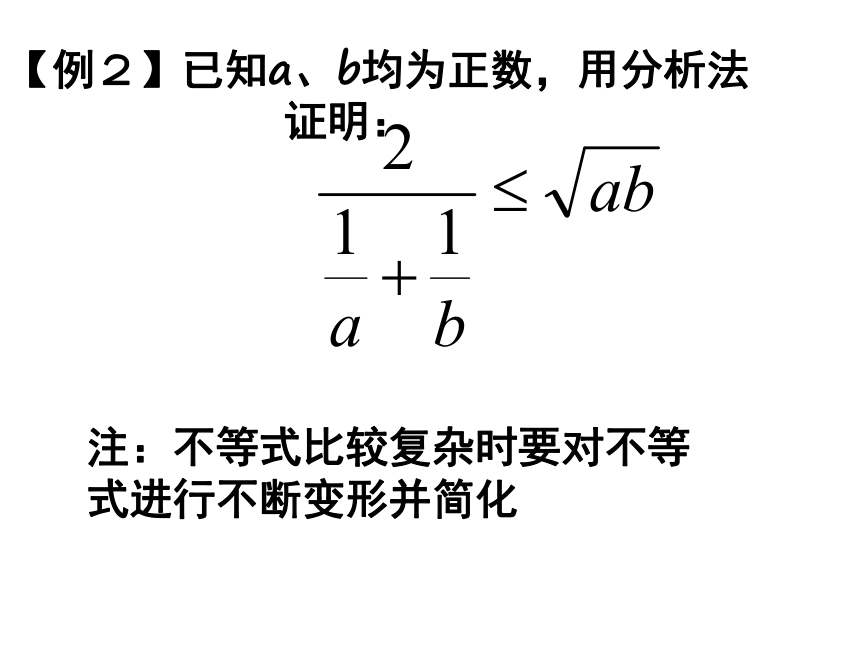
宜用分析法探究证明途径.【例2】已知a、b均为正数,用分析法
证明: 注:不等式比较复杂时要对不等式进行不断变形并简化 (1)分析法的思维特点是:执果索因.
对于思路不明显,感到无从下手的问题宜用分析法探究证明途径.
另外,不等式的证明告诉我们可以对不等式做这样或那样的变形,分析时贵在变形,不通思变,变则通!
小结:思考题:尝试用分析法证明书本P22例3作业P26: 3 、 4。【例2】已知a、b、m均为正数,且a
用分析法证明 例1.求证:分析法:证明不等式,有时可以从求证的
不等式出发,分析使这个不等式
成立的充分条件,把证明不等式
转化为判定这些充分条件是否具
备的问题。如果能够肯定这些充分
条件都已具备,那么就可以判定
原不等式成立。这种证明方法通常
叫做分析法 逻辑关系为: 【例3】(1)已知a>1,求证: (2)已知a>0,b>0,c>0,求证: 【例4】(课本例)证明:通过水管放水,
当流速相等时,如果水管截面(指横截面)
的周长相等,那么截面的圆的水管比截面
是正方形的水管流量大。例5.已知a>b>0,求证:
分析法引例
证明:1、作差法:作差——变形——定符号
2、分析法的特点是:执果索因. 分析时贵在变形,不通思变,变则通! 用分析法证明不等式的模式是:
要证B成立
只要证 成立
只要证 成立
只要A成立
今已知A成立
故B得证.例1.求证:注:对于思路不明显,感到无从下手的问题
宜用分析法探究证明途径.【例2】已知a、b均为正数,用分析法
证明: 注:不等式比较复杂时要对不等式进行不断变形并简化 (1)分析法的思维特点是:执果索因.
对于思路不明显,感到无从下手的问题宜用分析法探究证明途径.
另外,不等式的证明告诉我们可以对不等式做这样或那样的变形,分析时贵在变形,不通思变,变则通!
小结:思考题:尝试用分析法证明书本P22例3作业P26: 3 、 4。【例2】已知a、b、m均为正数,且a
用分析法证明 例1.求证:分析法:证明不等式,有时可以从求证的
不等式出发,分析使这个不等式
成立的充分条件,把证明不等式
转化为判定这些充分条件是否具
备的问题。如果能够肯定这些充分
条件都已具备,那么就可以判定
原不等式成立。这种证明方法通常
叫做分析法 逻辑关系为: 【例3】(1)已知a>1,求证: (2)已知a>0,b>0,c>0,求证: 【例4】(课本例)证明:通过水管放水,
当流速相等时,如果水管截面(指横截面)
的周长相等,那么截面的圆的水管比截面
是正方形的水管流量大。例5.已知a>b>0,求证:
