3.3幂函数 课件(共19张PPT)-2024-2025学年高一上学期数学人教A版(2019)必修第一册
文档属性
| 名称 | 3.3幂函数 课件(共19张PPT)-2024-2025学年高一上学期数学人教A版(2019)必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-04 05:52:21 | ||
图片预览






文档简介
(共19张PPT)
幂函数
高中数学人教A版必修第一册(新课标)
(1)如果张红以1元/kg的价格购买了某种蔬菜wkg, 那么她需要支付p=w元, 这
里p是w的函数;
(2)如果正方形的边长为a, 那么正方形的面积S=a2 , 这里S是a的函数;
(3)如果立方体的边长为b, 那么立方体的体积V=b3 , 这里V是b的函数;
(4)如果一个正方形场地的面积为S, 那么正方形的边长c= , 这里c是S的函数;
(5)如果某人ts内骑车行进1 km, 那么他骑车的平均速度v= ,这里v是t的函数 .
问题1 观察(1) ~(5) 中的函数解析式, 你能发现它们的共
同特征吗?
问题导入
y=x0 ,y=x4 ,y=x-2 ,y= 等 .
问题1 观察(1) ~(5) 中的函数解析式, 你能发现它们的共
同特征吗?
问题导入
追问1 你还能举几个相同结构的函数的例子吗?
共同特征是: 函数解析式是幂的形式, 且指数是常数,底数是自变量 .
幂函数定义:
一般地, 函数y=xα叫做幂函数(power function) , 其中x为自变量,
α为常数 .
对于幂函数, 我们只研究α= 1, 2, 3, , -1时的图象与性质 .
问题导入
(1) 函数的对应关系的表示、定义域、值域、单调性和奇偶性等 .
(2)通常先根据函数解析式求出函数的定义域, 画出函数的图象; 再
利用图象和解析式, 讨论函数的值域、单调性、奇偶性等问题 .
(2)你能类比前面讨论函数性质时的思路, 提出研究幂函数性质的方
法吗?
问题2 (1)对于一类新函数,请你思考我们需要从哪些方面
入手去研究?
新知探究
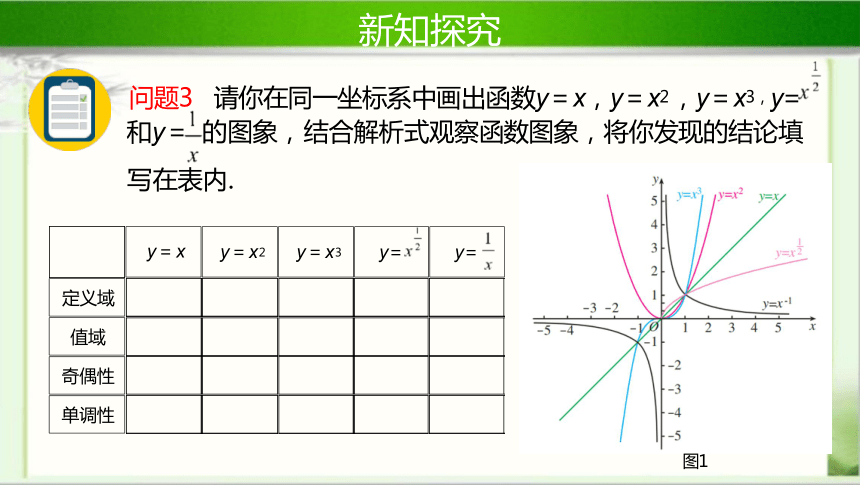
问题3 请你在同一坐标系中画出函数y=x,y=x2 ,y=x3,y= 和y= 的图象, 结合解析式观察函数图象,将你发现的结论填
写在表内.
新知探究
y=x
y=x2
y=x3
y=
y=
奇偶性
单调性
定义域
值域
图1
新知探究
问题3 请你在同一坐标系中画出函数y=x,y=x2 ,y=x3,y= 和y= 的图象, 结合解析式观察函数图象,将你发现的结论填
写在表内 .
在( - ∞ , 0)上 单调递减,在(0, +∞) 上单调递增
在( - ∞ , 0), (0, +∞) 上 单调递减
在( - ∞ , + ∞) 上单调递 增
在( - ∞ , + ∞) 上单调递 增
在[0, +∞)
上单调递增
y=x2
y=
y=x3
y=x
y=
单调性
R
奇函数
{y|y≥0}
{x|x≠0}
奇函数
R
{y|y≠0}
奇函数
R
R
{x|x≥0}
奇函数
非奇非偶函数
R
{y|y≥0}
定义域
奇偶性
值域
表1
追问2 这5个幂函数的图象均过第一象限, 如何确定是否过第二或第
三象限?
如果定义域为{x|x≥0}, 则不过第二、三象限, 比如y= ;
如果定义域包含( - ∞ , 0) , 可以结合奇偶性判断,
如果为偶函数, 则过第二象限, 比如y=x2;
如果为奇函数, 则过第三象限, 比如y=x和y=x3 .
新知探究
追问1 结合图1和表1, 你能总结出这5个幂函数的共性吗?
图象都过点(1, 1) , 图象都经过第一象限 .
新知探究
追问3 在第一象限中, 如何区分这5个函数的图象?
y= 在(0, +∞) 上单调递减, 图象向上与y轴无限接近,
向右与x轴无限接近, 其余均单调递增. y=x的图象是一条直线,
其余全是曲线; 当0<x<1时,
当x>1时,y=x的图象
位于该直线的下方 .
相比y= 的图象,y=x2
和y=x3 的图象与y=x的
图象的位置关系正好相
反(如图2),
y=x的图象位于该直线的上方;
图2
新知探究
追问3 在第一象限中, 如何区分这5个函数的图象?
即: 当0<x<1时,y=x2 的图象位于y=x3 的图象的上方,
当x>1时,y=x2 的图象位于y=x3 的图象的下方(如图3) .
图3
例1 证明幂函数 f(x)= 是增函数 .
证明: 函数的定义域是[0, +∞) .
x1 ,x2 ∈[0, +∞) , 且x1<x2,
f(x1 )-f(x2 )= = = 因为x1-x2<0, >0, 所以f(x1 )<f(x2 ), 即幂函数f(x)= 是增函数 .
新知探究
解:(1)( -1.5)3和( -1.4)3可看作函数y=x3 当x分别取-1.5和
- 1.4时所对应的两个函数值 .
y=x3在( - ∞ , +∞) 上单调递增,
因为-1.5< -1.4, 所以( -1.5)3 <( -1.4)3 .
新知探究
例2 利用幂函数的性质, 比较下列各题中两个值的大小: (1)( -1.5)3 ,( -1.4)3; (2)
新知探究
例2 利用幂函数的性质, 比较下列各题中两个值的大小: (1)( -1.5)3 ,( -1.4)3; (2)
解:(2) 和 可看作函数y= 当x分别取-1.5和-1.4时所
对应的两个函数值 .
y= 在( - ∞ , +∞) 上单调递增,
因为-1.5< -1.4, 所 以
归纳小结
问题4 回忆本节课的内容,请你回答以下几个问题:
(1)什么是幂函数?你能简单说一说本节课所学的5个幂函数的
性质吗?
(2)你能说说幂函数和正比例函数, 反比例函数, 二次函数的区别和
联系吗?
(1)概念和性质略;
(2)幂函数和正比例函数, 反比例函数, 二次函数的交集分别是y=
x,y= ,y=x2 , 除此之外, 别无交集 .
答案:y= ,x≥0 .
1. 已知幂函数y=f(x)的图象过点(2, ), 求这个函数的解析
式.
目标检测
目标检测
2. 根据单调性和奇偶性的定义证明函数f(x)=x3 的单调性和奇偶
性.
证明: 因为函数f(x)=x3定义域为R.
x∈R , 都有-x∈R , 且f(-x)=(-x)3 =-x3 =-f(x),
函数f(x)=x3为奇函数 .
任取x1 ,x2 ∈R , 且x1<x2,
目标检测
2. 根据单调性和奇偶性的定义证明函数f(x)=x3 的单调性和奇偶
性.
证明:f(x1 )-f(x2 )=(x1-x2 ) [x12+x1x2+x22]
=(x1-x2 ) [x12+x1x2 + x22 + x22]
=(x1-x2 ) [(x12 + x2 )2 + x22] .
因为x1-x2<0,(x12 + x2 )2 + x22>0, 所以f(x1 )<f(x2 ),
即幂函数f(x)=x3是增函数 .
谢谢大家
敬请各位老师提出宝贵意见!
再见
再见
幂函数
高中数学人教A版必修第一册(新课标)
(1)如果张红以1元/kg的价格购买了某种蔬菜wkg, 那么她需要支付p=w元, 这
里p是w的函数;
(2)如果正方形的边长为a, 那么正方形的面积S=a2 , 这里S是a的函数;
(3)如果立方体的边长为b, 那么立方体的体积V=b3 , 这里V是b的函数;
(4)如果一个正方形场地的面积为S, 那么正方形的边长c= , 这里c是S的函数;
(5)如果某人ts内骑车行进1 km, 那么他骑车的平均速度v= ,这里v是t的函数 .
问题1 观察(1) ~(5) 中的函数解析式, 你能发现它们的共
同特征吗?
问题导入
y=x0 ,y=x4 ,y=x-2 ,y= 等 .
问题1 观察(1) ~(5) 中的函数解析式, 你能发现它们的共
同特征吗?
问题导入
追问1 你还能举几个相同结构的函数的例子吗?
共同特征是: 函数解析式是幂的形式, 且指数是常数,底数是自变量 .
幂函数定义:
一般地, 函数y=xα叫做幂函数(power function) , 其中x为自变量,
α为常数 .
对于幂函数, 我们只研究α= 1, 2, 3, , -1时的图象与性质 .
问题导入
(1) 函数的对应关系的表示、定义域、值域、单调性和奇偶性等 .
(2)通常先根据函数解析式求出函数的定义域, 画出函数的图象; 再
利用图象和解析式, 讨论函数的值域、单调性、奇偶性等问题 .
(2)你能类比前面讨论函数性质时的思路, 提出研究幂函数性质的方
法吗?
问题2 (1)对于一类新函数,请你思考我们需要从哪些方面
入手去研究?
新知探究
问题3 请你在同一坐标系中画出函数y=x,y=x2 ,y=x3,y= 和y= 的图象, 结合解析式观察函数图象,将你发现的结论填
写在表内.
新知探究
y=x
y=x2
y=x3
y=
y=
奇偶性
单调性
定义域
值域
图1
新知探究
问题3 请你在同一坐标系中画出函数y=x,y=x2 ,y=x3,y= 和y= 的图象, 结合解析式观察函数图象,将你发现的结论填
写在表内 .
在( - ∞ , 0)上 单调递减,在(0, +∞) 上单调递增
在( - ∞ , 0), (0, +∞) 上 单调递减
在( - ∞ , + ∞) 上单调递 增
在( - ∞ , + ∞) 上单调递 增
在[0, +∞)
上单调递增
y=x2
y=
y=x3
y=x
y=
单调性
R
奇函数
{y|y≥0}
{x|x≠0}
奇函数
R
{y|y≠0}
奇函数
R
R
{x|x≥0}
奇函数
非奇非偶函数
R
{y|y≥0}
定义域
奇偶性
值域
表1
追问2 这5个幂函数的图象均过第一象限, 如何确定是否过第二或第
三象限?
如果定义域为{x|x≥0}, 则不过第二、三象限, 比如y= ;
如果定义域包含( - ∞ , 0) , 可以结合奇偶性判断,
如果为偶函数, 则过第二象限, 比如y=x2;
如果为奇函数, 则过第三象限, 比如y=x和y=x3 .
新知探究
追问1 结合图1和表1, 你能总结出这5个幂函数的共性吗?
图象都过点(1, 1) , 图象都经过第一象限 .
新知探究
追问3 在第一象限中, 如何区分这5个函数的图象?
y= 在(0, +∞) 上单调递减, 图象向上与y轴无限接近,
向右与x轴无限接近, 其余均单调递增. y=x的图象是一条直线,
其余全是曲线; 当0<x<1时,
当x>1时,y=x的图象
位于该直线的下方 .
相比y= 的图象,y=x2
和y=x3 的图象与y=x的
图象的位置关系正好相
反(如图2),
y=x的图象位于该直线的上方;
图2
新知探究
追问3 在第一象限中, 如何区分这5个函数的图象?
即: 当0<x<1时,y=x2 的图象位于y=x3 的图象的上方,
当x>1时,y=x2 的图象位于y=x3 的图象的下方(如图3) .
图3
例1 证明幂函数 f(x)= 是增函数 .
证明: 函数的定义域是[0, +∞) .
x1 ,x2 ∈[0, +∞) , 且x1<x2,
f(x1 )-f(x2 )= = = 因为x1-x2<0, >0, 所以f(x1 )<f(x2 ), 即幂函数f(x)= 是增函数 .
新知探究
解:(1)( -1.5)3和( -1.4)3可看作函数y=x3 当x分别取-1.5和
- 1.4时所对应的两个函数值 .
y=x3在( - ∞ , +∞) 上单调递增,
因为-1.5< -1.4, 所以( -1.5)3 <( -1.4)3 .
新知探究
例2 利用幂函数的性质, 比较下列各题中两个值的大小: (1)( -1.5)3 ,( -1.4)3; (2)
新知探究
例2 利用幂函数的性质, 比较下列各题中两个值的大小: (1)( -1.5)3 ,( -1.4)3; (2)
解:(2) 和 可看作函数y= 当x分别取-1.5和-1.4时所
对应的两个函数值 .
y= 在( - ∞ , +∞) 上单调递增,
因为-1.5< -1.4, 所 以
归纳小结
问题4 回忆本节课的内容,请你回答以下几个问题:
(1)什么是幂函数?你能简单说一说本节课所学的5个幂函数的
性质吗?
(2)你能说说幂函数和正比例函数, 反比例函数, 二次函数的区别和
联系吗?
(1)概念和性质略;
(2)幂函数和正比例函数, 反比例函数, 二次函数的交集分别是y=
x,y= ,y=x2 , 除此之外, 别无交集 .
答案:y= ,x≥0 .
1. 已知幂函数y=f(x)的图象过点(2, ), 求这个函数的解析
式.
目标检测
目标检测
2. 根据单调性和奇偶性的定义证明函数f(x)=x3 的单调性和奇偶
性.
证明: 因为函数f(x)=x3定义域为R.
x∈R , 都有-x∈R , 且f(-x)=(-x)3 =-x3 =-f(x),
函数f(x)=x3为奇函数 .
任取x1 ,x2 ∈R , 且x1<x2,
目标检测
2. 根据单调性和奇偶性的定义证明函数f(x)=x3 的单调性和奇偶
性.
证明:f(x1 )-f(x2 )=(x1-x2 ) [x12+x1x2+x22]
=(x1-x2 ) [x12+x1x2 + x22 + x22]
=(x1-x2 ) [(x12 + x2 )2 + x22] .
因为x1-x2<0,(x12 + x2 )2 + x22>0, 所以f(x1 )<f(x2 ),
即幂函数f(x)=x3是增函数 .
谢谢大家
敬请各位老师提出宝贵意见!
再见
再见
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
