陕西省西安市周至县2023-2024学年高一下学期7月期末教学质量检测数学试题(含答案)
文档属性
| 名称 | 陕西省西安市周至县2023-2024学年高一下学期7月期末教学质量检测数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 632.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-04 21:32:53 | ||
图片预览


文档简介
陕西省西安市周至县2023-2024学年高一下学期7月期末教学质量检测数学试题
注意事项:
1.答题前,考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知向量,若,则
A. B. C. D.
2.某公司在职员工有1200人,其中销售人员有400人,研发人员有600人,现采用分层随机抽样的方法抽取120人进行调研,则被抽到的研发人员人数比销售人员人数多
A.20 B.30 C.40 D.50
3.投掷一枚质地均匀的骰子,则向上的点数是3的倍数的概率为
A. B. C. D.
4.已知直线,平面,若,则“”是“”的
A.充要条件 B.必要不充分条件 C.充分不必要条件 D.既不充分也不必要条件
5.在一个港口,有一艘船以每小时30海里的速度向正东方向行驶,在某时观测到在该船北偏东方向上有一座灯塔A,2小时后,灯塔在该船的东北方向上,该船继续向正东方向行驶足够长时间,则该船与灯塔之间的最短距离是
A.海里 B.海里 C.海里 D.海里
6.若,则
A.0 B.1 C. D.2
7.已知某圆柱的轴截面是正方形,且上、下底面圆周上的所有点都在球的表面上,则该圆柱的体积与球的体积的比值是
A. B. C. D.
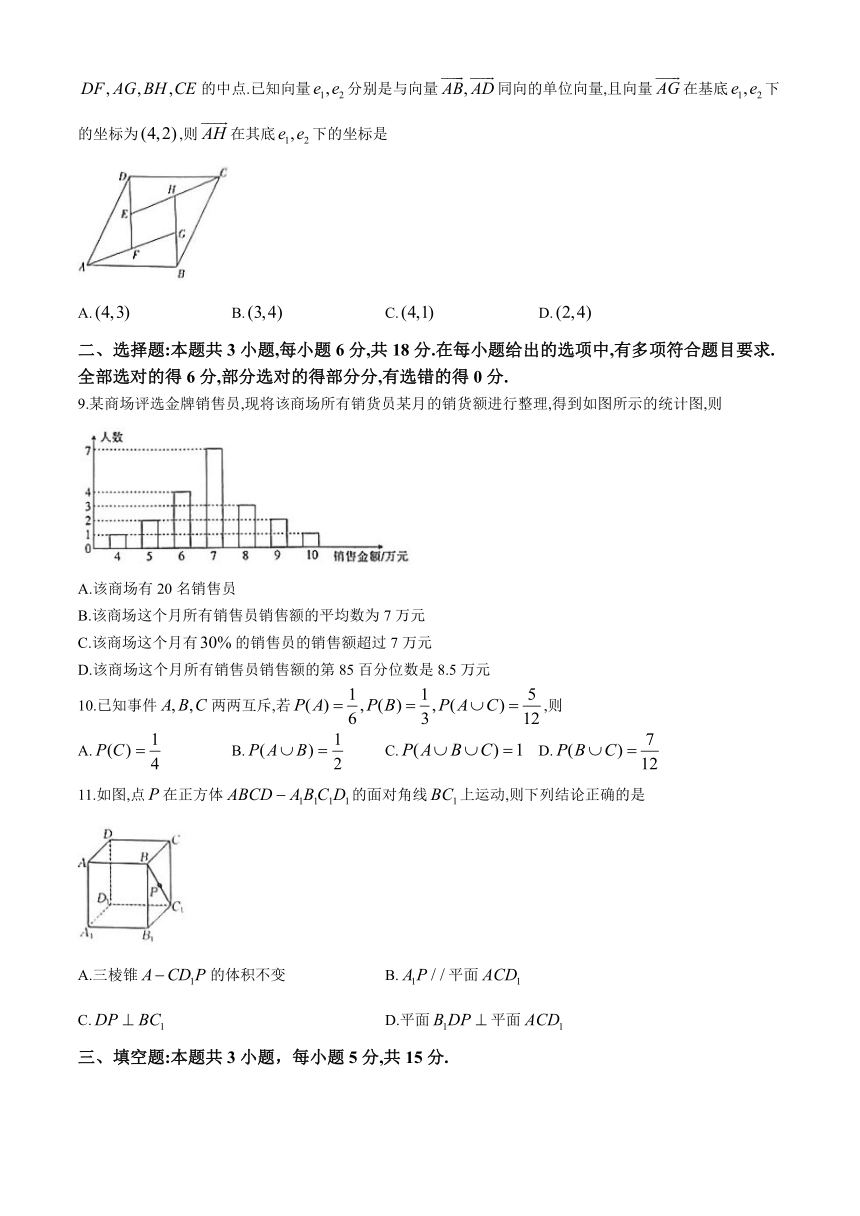
8.若向量是一组基底,向量.则称为向是在基底下的坐标.如图,某人仿照赵爽弦图,用四个三角形和一个小的平行四边形拼成一个大平行四边形,其中分别是的中点.已知向量分别是与向量同向的单位向量,且向量在基底下的坐标为,则在其底下的坐标是
A. B. C. D.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.某商场评选金牌销售员,现将该商场所有销货员某月的销货额进行整理,得到如图所示的统计图,则
A.该商场有20名销售员
B.该商场这个月所有销售员销售额的平均数为7万元
C.该商场这个月有的销售员的销售额超过7万元
D.该商场这个月所有销售员销售额的第85百分位数是8.5万元
10.已知事件两两互斥,若,则
A. B. C. D.
11.如图,点在正方体的面对角线上运动,则下列结论正确的是
A.三棱锥的体积不变 B.平面
C. D.平面平面
三、填空题:本题共3小题,每小题5分,共15分.
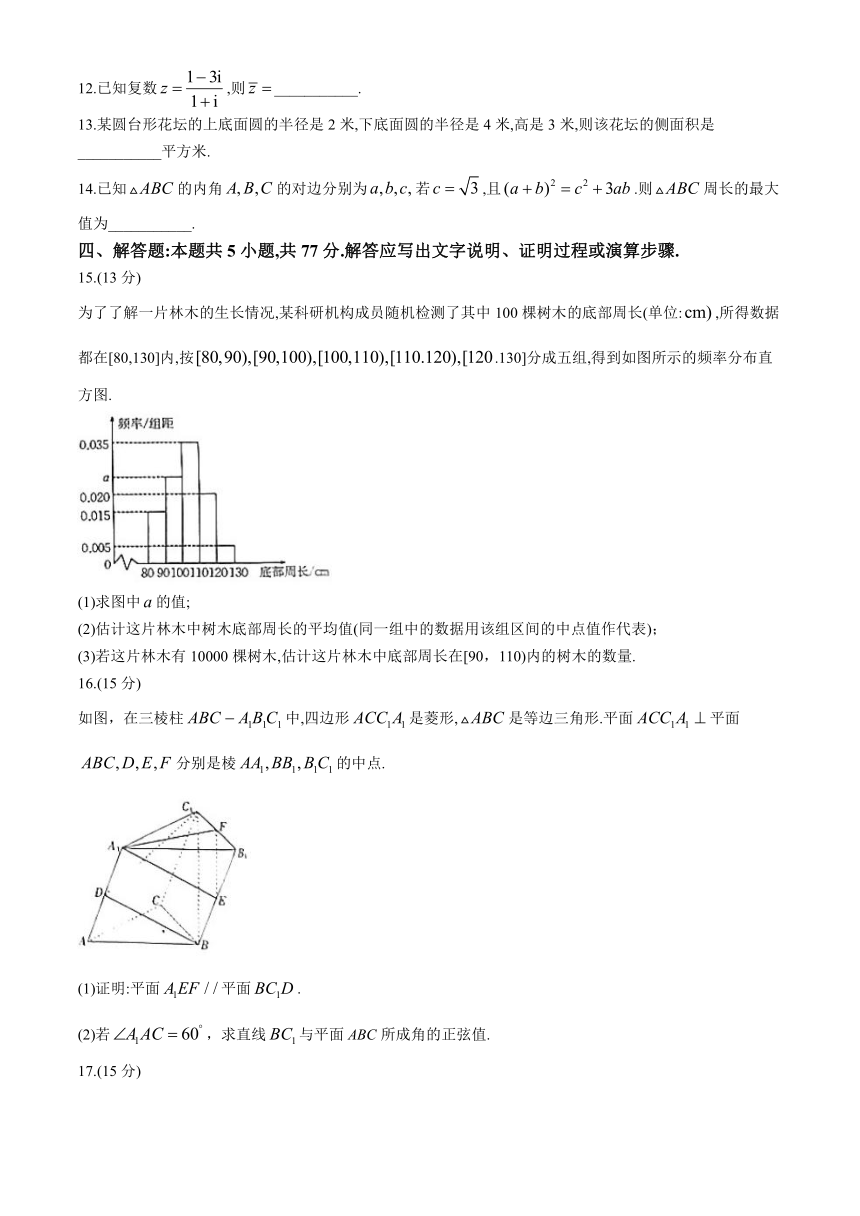
12.已知复数,则___________.
13.某圆台形花坛的上底面圆的半径是2米,下底面圆的半径是4米,高是3米,则该花坛的侧面积是___________平方米.
14.已知的内角的对边分别为若,且.则周长的最大值为___________.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)
为了了解一片林木的生长情况,某科研机构成员随机检测了其中100棵树木的底部周长(单位:,所得数据都在[80,130]内,按.130]分成五组,得到如图所示的频率分布直方图.
(1)求图中的值;
(2)估计这片林木中树木底部周长的平均值(同一组中的数据用该组区间的中点值作代表);
(3)若这片林木有10000棵树木,估计这片林木中底部周长在[90,110)内的树木的数量.
16.(15分)
如图,在三棱柱中,四边形是菱形,是等边三角形.平面平面分别是棱的中点.
(1)证明:平面平面.
(2)若,求直线与平面ABC所成角的正弦值.
17.(15分)
在△ABC中,角的对边分别是已知,且.
(1)求的值;
(2)若,求的周长.
18.(17分)
如图,这是某种型号的奖杯,它是用一个正四棱台、一个正四棱柱和一个球焊接而成的,球的半径为.正四棱柱的底面边长为2R,高为7R.正四棱台的上、下底面边长分别为4R和6R,斜高(即侧面梯形的高)为3R.
(1)求这种型号的奖杯的表而积(用R表示,焊接处对面积的影响忽略不计);
(2)已知R=3cm,若为奖杯表面镀金所用的材料每可以涂,且该种型号的奖杯底面(图中正四棱台的下底面作为该种型号的奖杯的底面,一般底面采用其他材质)不需要镀金,则为100个这种型号的奖杯镀金约需要多少材料?(π取3.14,精确到0.01g)
19.(17分)
甲、乙、丙三人进行台球比赛,比赛规则如下:先由两人上场比赛,第三人旁观,一局结束后,败者下场作为旁观者,原旁观者上场与胜者比赛,按此规则循环下去,若比赛中有人累计获胜3局,则此人获得最终胜利,比赛结束.三人经过抽签决定由甲、乙先上场比赛,丙作为旁观者,根据以往经验,每局比赛中,甲、乙比甲胜的概率为,乙、丙比赛乙胜的概率为,丙、甲比赛丙胜的概率为,每局比赛相互独立,且每局比赛没有平局.
(1)当比赛完3局时,求甲、乙、丙各旁观1局的概率;
(2)已知比赛进行5局后结束,求甲获得最终胜利的概率.
高一数学教学质量检测
参考答案
1.D 因为,所以.因为,所以,即,解得.
2.A 由题意可得被抽到的研发人员有人,销售人员有人,则被抽到的研发人员人数比销售人员人数多.
3.B 向上的点数是3的倍数的概率为.
4.C 由,得.由,得或,则“”是“”的充分不必要条件.
5.D 设该船的初始位置为B,2小时后的位置为,过作,垂足为(图略),则AD为所求的最短距离.由题意可知海里,则.在中,由正弦定理可得,则海里.在Rt中,海里,则海里.
6.D 因为,所以.
7.D 设该圆柱的底面圆半径为,高为,则.设球的半径为,则.由圆柱的体积公式可得.由球的体积公式可得,则.
8.B 由题意可得.因为EFGH是平行四边形,所以,所以,所以.因为向量在基底下的坐标为,所以,.因为,所以在基底下的坐标是.
9. 由统计图可知该商场有20名销售员,则正确.该商场这个月所有销售员销售额的平均数为万元,则错误.该商场这个月销售额超过7万元的销售员有6人,占总人数的百分比为,则C正确.因为,所以该商场这个月所有销售员销售额的第85百分位数是万元,则正确.
10. 因为事件两两互斥,所以.因为,所以,则正确.因为,所以,则正确.因为事件两两互斥,所以,则错误.因为,所以,则正确.
11. 由正方体的性质可知,则平面,则点到平面的距离为定值,所以三棱锥的体积不变,则正确.由正方体的性质易证平面平面.因为平面,所以平面,则B正确.当为的中点时,,当不是的中点时,DP与不垂直,则错误.由正方体的性质易证平面.因为平面,所以平面平面,则正确.
12. 因为,所以.
13. 由题意可得该花坛的母线长,则该花坛的侧面积平方米.
14. 因为,所以.因为,当且仅当时,等号成立,所以,即,所以.因为,所以,所以,则,即周长的最大值为.
15.解:(1)由频率分布直方图可得,解得0.025.4分
(2)设这片林木中树木底部周长的平均值为,
则分
(3)由频率分布直方图可知这片林木中树木的底部周长在内的频率是,
……………………………………………………………………………………………………………………10分
则这片林木中底部周长在内的树木的数量的估计值是.…………………13分
16.(1)证明:由三棱柱的定义可知AA1∥BB1,AA1=BB1.…………………………………………………………1分
因为D,E分别是棱的中点,所以,…………………………………………2分
所以四边形是平行四边形,则.……………………………………………………………3分
因为平面平面,所以平面.………………………………………4分
因为E,F分别是棱的中点,所以.………………………………………………………5分
因为平面平面,所以平面.………………………………………6分
因为平面,且,所以平面平面.…………………………7分
(2)解:作的延长线于点,连接BH.
因为平面平面ABC,且平面平面AC,所以平面ABC,
则是直线与平面ABC所成的角.....……………………………………………………8分
设,则.
因为,所以,则……………………………………10分
因为是等边三角形,所以,所以.
由余弦定理可得.………………………………12分
因为平面平面ABC,所以,则,………13分
故,即直线与平面ABC所成角的正弦值为分
17.解:(1)因为,所以.……………………………………2分
由正弦定理可得,则.……………………………………4分
因为,所以,则.………………………………………………………6分
(2)由余弦定理可得,
则,从而,………………………………………………………8分
即,解得或.……………………………………………………………11分
当时,,则的周长为;…………………………………………………13分
当时,,则的周长为.……………………………………………………15分
18.解:(1)球的表面积为.…………………………………………………………………………2分
正四棱柱的表面积为.…………………………………………………4分
正四棱台的表面积为.………………………………6分
故这种型号的奖杯的表面积为8分
(2)因为1个这种型号的奖杯需要镀金的面积为………………9分
,…………………………………………………………………11分
所以100个这种型号的奖杯需要镀金的面积为.…………14分
因为为奖杯表面镀金所用的材料每可以涂,所以为100个这种型号的奖杯镀金约需要材料.………………………………………………………………………17分
19.解:(1)由题意可知甲、乙、丙各旁观1局只需讨论前2局的胜负情况,情况如下:甲胜乙,丙胜甲;乙胜甲,丙胜乙.………………………………………………………………………………………………………1分
设甲、乙比赛甲胜,乙、丙比赛乙胜,丙、甲比赛丙胜分别为事件A,B,C,且A,B,C相互独立.
设比赛完3局时,甲、乙、丙各旁观1局为事件,则,…………………3分
则分
即甲、乙、丙各旁观1局的概率为.………………………………………………………………………6分
(2)设甲、乙、丙第局比赛获胜分别为事件,
设比赛完5局甲获得最终胜利为事件,
则.……8分
因为,……………9分
,…………………10分
,…………………11分
,…………………12分
…………………13分
…………………14分
所以.……………………………………………………16分
故比赛进行5局后结束,甲获得最终胜利的概率为.…………………………………………………17分
注意事项:
1.答题前,考生务必将自己的姓名、考生号、考场号、座位号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知向量,若,则
A. B. C. D.
2.某公司在职员工有1200人,其中销售人员有400人,研发人员有600人,现采用分层随机抽样的方法抽取120人进行调研,则被抽到的研发人员人数比销售人员人数多
A.20 B.30 C.40 D.50
3.投掷一枚质地均匀的骰子,则向上的点数是3的倍数的概率为
A. B. C. D.
4.已知直线,平面,若,则“”是“”的
A.充要条件 B.必要不充分条件 C.充分不必要条件 D.既不充分也不必要条件
5.在一个港口,有一艘船以每小时30海里的速度向正东方向行驶,在某时观测到在该船北偏东方向上有一座灯塔A,2小时后,灯塔在该船的东北方向上,该船继续向正东方向行驶足够长时间,则该船与灯塔之间的最短距离是
A.海里 B.海里 C.海里 D.海里
6.若,则
A.0 B.1 C. D.2
7.已知某圆柱的轴截面是正方形,且上、下底面圆周上的所有点都在球的表面上,则该圆柱的体积与球的体积的比值是
A. B. C. D.
8.若向量是一组基底,向量.则称为向是在基底下的坐标.如图,某人仿照赵爽弦图,用四个三角形和一个小的平行四边形拼成一个大平行四边形,其中分别是的中点.已知向量分别是与向量同向的单位向量,且向量在基底下的坐标为,则在其底下的坐标是
A. B. C. D.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.某商场评选金牌销售员,现将该商场所有销货员某月的销货额进行整理,得到如图所示的统计图,则
A.该商场有20名销售员
B.该商场这个月所有销售员销售额的平均数为7万元
C.该商场这个月有的销售员的销售额超过7万元
D.该商场这个月所有销售员销售额的第85百分位数是8.5万元
10.已知事件两两互斥,若,则
A. B. C. D.
11.如图,点在正方体的面对角线上运动,则下列结论正确的是
A.三棱锥的体积不变 B.平面
C. D.平面平面
三、填空题:本题共3小题,每小题5分,共15分.
12.已知复数,则___________.
13.某圆台形花坛的上底面圆的半径是2米,下底面圆的半径是4米,高是3米,则该花坛的侧面积是___________平方米.
14.已知的内角的对边分别为若,且.则周长的最大值为___________.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)
为了了解一片林木的生长情况,某科研机构成员随机检测了其中100棵树木的底部周长(单位:,所得数据都在[80,130]内,按.130]分成五组,得到如图所示的频率分布直方图.
(1)求图中的值;
(2)估计这片林木中树木底部周长的平均值(同一组中的数据用该组区间的中点值作代表);
(3)若这片林木有10000棵树木,估计这片林木中底部周长在[90,110)内的树木的数量.
16.(15分)
如图,在三棱柱中,四边形是菱形,是等边三角形.平面平面分别是棱的中点.
(1)证明:平面平面.
(2)若,求直线与平面ABC所成角的正弦值.
17.(15分)
在△ABC中,角的对边分别是已知,且.
(1)求的值;
(2)若,求的周长.
18.(17分)
如图,这是某种型号的奖杯,它是用一个正四棱台、一个正四棱柱和一个球焊接而成的,球的半径为.正四棱柱的底面边长为2R,高为7R.正四棱台的上、下底面边长分别为4R和6R,斜高(即侧面梯形的高)为3R.
(1)求这种型号的奖杯的表而积(用R表示,焊接处对面积的影响忽略不计);
(2)已知R=3cm,若为奖杯表面镀金所用的材料每可以涂,且该种型号的奖杯底面(图中正四棱台的下底面作为该种型号的奖杯的底面,一般底面采用其他材质)不需要镀金,则为100个这种型号的奖杯镀金约需要多少材料?(π取3.14,精确到0.01g)
19.(17分)
甲、乙、丙三人进行台球比赛,比赛规则如下:先由两人上场比赛,第三人旁观,一局结束后,败者下场作为旁观者,原旁观者上场与胜者比赛,按此规则循环下去,若比赛中有人累计获胜3局,则此人获得最终胜利,比赛结束.三人经过抽签决定由甲、乙先上场比赛,丙作为旁观者,根据以往经验,每局比赛中,甲、乙比甲胜的概率为,乙、丙比赛乙胜的概率为,丙、甲比赛丙胜的概率为,每局比赛相互独立,且每局比赛没有平局.
(1)当比赛完3局时,求甲、乙、丙各旁观1局的概率;
(2)已知比赛进行5局后结束,求甲获得最终胜利的概率.
高一数学教学质量检测
参考答案
1.D 因为,所以.因为,所以,即,解得.
2.A 由题意可得被抽到的研发人员有人,销售人员有人,则被抽到的研发人员人数比销售人员人数多.
3.B 向上的点数是3的倍数的概率为.
4.C 由,得.由,得或,则“”是“”的充分不必要条件.
5.D 设该船的初始位置为B,2小时后的位置为,过作,垂足为(图略),则AD为所求的最短距离.由题意可知海里,则.在中,由正弦定理可得,则海里.在Rt中,海里,则海里.
6.D 因为,所以.
7.D 设该圆柱的底面圆半径为,高为,则.设球的半径为,则.由圆柱的体积公式可得.由球的体积公式可得,则.
8.B 由题意可得.因为EFGH是平行四边形,所以,所以,所以.因为向量在基底下的坐标为,所以,.因为,所以在基底下的坐标是.
9. 由统计图可知该商场有20名销售员,则正确.该商场这个月所有销售员销售额的平均数为万元,则错误.该商场这个月销售额超过7万元的销售员有6人,占总人数的百分比为,则C正确.因为,所以该商场这个月所有销售员销售额的第85百分位数是万元,则正确.
10. 因为事件两两互斥,所以.因为,所以,则正确.因为,所以,则正确.因为事件两两互斥,所以,则错误.因为,所以,则正确.
11. 由正方体的性质可知,则平面,则点到平面的距离为定值,所以三棱锥的体积不变,则正确.由正方体的性质易证平面平面.因为平面,所以平面,则B正确.当为的中点时,,当不是的中点时,DP与不垂直,则错误.由正方体的性质易证平面.因为平面,所以平面平面,则正确.
12. 因为,所以.
13. 由题意可得该花坛的母线长,则该花坛的侧面积平方米.
14. 因为,所以.因为,当且仅当时,等号成立,所以,即,所以.因为,所以,所以,则,即周长的最大值为.
15.解:(1)由频率分布直方图可得,解得0.025.4分
(2)设这片林木中树木底部周长的平均值为,
则分
(3)由频率分布直方图可知这片林木中树木的底部周长在内的频率是,
……………………………………………………………………………………………………………………10分
则这片林木中底部周长在内的树木的数量的估计值是.…………………13分
16.(1)证明:由三棱柱的定义可知AA1∥BB1,AA1=BB1.…………………………………………………………1分
因为D,E分别是棱的中点,所以,…………………………………………2分
所以四边形是平行四边形,则.……………………………………………………………3分
因为平面平面,所以平面.………………………………………4分
因为E,F分别是棱的中点,所以.………………………………………………………5分
因为平面平面,所以平面.………………………………………6分
因为平面,且,所以平面平面.…………………………7分
(2)解:作的延长线于点,连接BH.
因为平面平面ABC,且平面平面AC,所以平面ABC,
则是直线与平面ABC所成的角.....……………………………………………………8分
设,则.
因为,所以,则……………………………………10分
因为是等边三角形,所以,所以.
由余弦定理可得.………………………………12分
因为平面平面ABC,所以,则,………13分
故,即直线与平面ABC所成角的正弦值为分
17.解:(1)因为,所以.……………………………………2分
由正弦定理可得,则.……………………………………4分
因为,所以,则.………………………………………………………6分
(2)由余弦定理可得,
则,从而,………………………………………………………8分
即,解得或.……………………………………………………………11分
当时,,则的周长为;…………………………………………………13分
当时,,则的周长为.……………………………………………………15分
18.解:(1)球的表面积为.…………………………………………………………………………2分
正四棱柱的表面积为.…………………………………………………4分
正四棱台的表面积为.………………………………6分
故这种型号的奖杯的表面积为8分
(2)因为1个这种型号的奖杯需要镀金的面积为………………9分
,…………………………………………………………………11分
所以100个这种型号的奖杯需要镀金的面积为.…………14分
因为为奖杯表面镀金所用的材料每可以涂,所以为100个这种型号的奖杯镀金约需要材料.………………………………………………………………………17分
19.解:(1)由题意可知甲、乙、丙各旁观1局只需讨论前2局的胜负情况,情况如下:甲胜乙,丙胜甲;乙胜甲,丙胜乙.………………………………………………………………………………………………………1分
设甲、乙比赛甲胜,乙、丙比赛乙胜,丙、甲比赛丙胜分别为事件A,B,C,且A,B,C相互独立.
设比赛完3局时,甲、乙、丙各旁观1局为事件,则,…………………3分
则分
即甲、乙、丙各旁观1局的概率为.………………………………………………………………………6分
(2)设甲、乙、丙第局比赛获胜分别为事件,
设比赛完5局甲获得最终胜利为事件,
则.……8分
因为,……………9分
,…………………10分
,…………………11分
,…………………12分
…………………13分
…………………14分
所以.……………………………………………………16分
故比赛进行5局后结束,甲获得最终胜利的概率为.…………………………………………………17分
同课章节目录
