2023-2024学年重庆市渝西南七校联考高二下学期期末考试数学试题(含答案)
文档属性
| 名称 | 2023-2024学年重庆市渝西南七校联考高二下学期期末考试数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 97.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-05 16:40:55 | ||
图片预览



文档简介
2023-2024学年重庆市渝西南七校联考高二下学期期末考试数学试题
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合,,则( )
A. B. C. D.
2.树人中学国旗班共有名学生,其中男女比例,平均身高,用等比例分层随机抽样的方法,从中抽取一个容量为的样本,若样本中男生的平均身高为,样本中女生人数与女生平均身高的估计值分别为( )
A. 人 B. 人 C. 人 D. 人
3.“”成立的一个充分条件可以是( )
A. B. C. D.
4.有名男生、名女生站成一排,则这名男生互不相邻的站法共有种
A. B. C. D.
5.已知,均为正实数,且,则的最小值为( )
A. B. C. D.
6.甲、乙、丙三人相互做传球训练,第次由甲将球传出,每次传球时,传球者都等可能地将球传给另外两个人中的任何一人,经过次传球后,球恰好在甲手中的概率为( )
A. B. C. D.
7.设,不等式在上恒成立,则的最大值为( )
A. B. C. D.
8.已知数列共有项,其中,且对每个,都有,则满足上述条件的数列一共有个。
A. B. C. D.
二、多选题:本题共3小题,共15分。在每小题给出的选项中,有多项符合题目要求。
9.下列命题中,正确的有( )
A. 若随机变量X~B(5,),则D(X)=
B. 若随机变量X~N(5,),且P(3X5)=0.3,则P(X7)=0.2
C. 若10件产品中有4件次品和6件正品.现从中随机抽取3件产品,记取得的次品数为随机变量X,无论是有放回的抽取还是无放回的抽取,D(X)相等
D. 从2,4,5,7,9,11,13,15,17,19中任取一个数,这个数比a大的概率为,若a恰为以上数据的第m百分位数,则m的值可能是60
10.袋中装有张相同的卡片,分别标有数字,,,,,从中有放回地随机取两次,每次取张卡片表示事件“第一次取出的卡片数字是奇数”,表示事件“第二次取出的卡片数字是偶数”,表示事件“两次取出的卡片数字之和是”,则( )
A. B. C. 与相互独立 D.
11.设,,,则下列结论中正确的是( )
A.
B. 若,,则
C. 当,时,
D. 当时,
三、填空题:本题共3小题,每小题5分,共15分。
12.已知不等式的解集为,则不等式的解集为 .
13.年月日至日“一节一赛”水上运动大赛在重庆彭水举行,甲、乙、丙、丁、戊名志愿者承担调度服务、安检服务、驾驶服务个项目志愿服务,每名志愿者需承担项工作,每项工作至少需要名志愿者,甲不承担驾驶服务,则不同的安排方法有 种用数字作答
14.已知函数的图像在其中为自然对数的底数处的切线斜率为若,且对任意恒成立,则的最大值为 .
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知函数.
讨论函数的单调性
若函数的图象是曲线,直线与曲线相切于点求函数在区间上的最大值和最小值.
16.本小题分
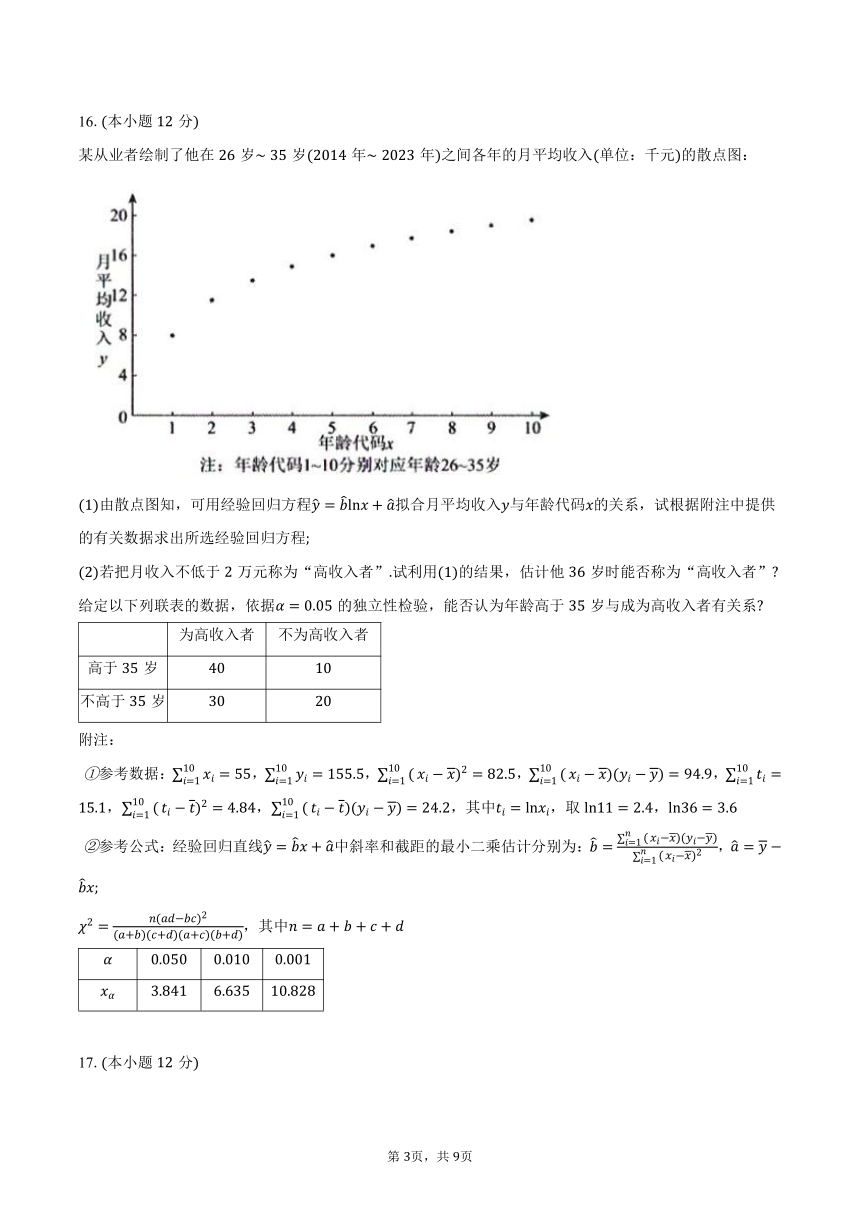
某从业者绘制了他在岁岁年年之间各年的月平均收入单位:千元的散点图:
由散点图知,可用经验回归方程拟合月平均收入与年龄代码的关系,试根据附注中提供的有关数据求出所选经验回归方程
若把月收入不低于万元称为“高收入者”试利用的结果,估计他岁时能否称为“高收入者”
给定以下列联表的数据,依据的独立性检验,能否认为年龄高于岁与成为高收入者有关系
为高收入者 不为高收入者
高于岁
不高于岁
附注:
参考数据:,,,,,,,其中,取,
参考公式:经验回归直线中斜率和截距的最小二乘估计分别为:,
,其中
17.本小题分
已知集合,集合.
若存在,使得,求的取值范围
若“”是“”的充分不必要条件,求实数的取值范围.
18.本小题分
某商场为了回馈广大顾客,设计了一个抽奖活动,在抽奖箱中放个大小相同的小球,其中个为红色,个为白色抽奖方式为:每名顾客进行两次抽奖,每次抽奖从抽奖箱中一次性摸出两个小球如果每次抽奖摸出的两个小球颜色相同即为中奖,两个小球颜色不同即为不中奖.
若规定第一次抽奖后将球放回抽奖箱,再进行第二次抽奖,求中奖次数的分布列和数学期望.
若规定第一次抽奖后不将球放回抽奖箱,直接进行第二次抽奖,求中奖次数的分布列和数学期望.
如果你是商场老板,如何在上述问两种抽奖方式中进行选择请写出你的选择及简要理由.
19.本小题分
给出以下三个材料:
若函数的导数为,的导数叫做的二阶导数,记作类似地,二阶导数的导数叫做的三阶导数,记作,三阶导数的导数叫做的四阶导数,一般地,阶导数的导数叫做的阶导数,即,
若,定义
若函数在包含的某个开区间上具有阶的导数,那么对于有,我们将称为函数在点处的阶泰勒展开式例如,在点处的阶泰勒展开式为根据以上三段材料,完成下面的题目:
若,在点处的阶泰勒展开式分别为,,求出,
比较中与的大小
证明:.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.或
13.
14.
15.解:,
当时,恒成立且不恒为,所有在上单调递增;
当时,令,解得或者,
所以在和上单调递增,
令,解得,
所以在上单调递减,
综上:当时,在上单调递增
当时,在和上单调递增,在上单调递减;
函数的图象是曲线,直线与曲线相切于点,
,,,即,
,
令,解得,
在上单调递减,
故在上的最大值为,最小值为.
16.解:令,则,
则,
;
,
,
回归方程为;
把带入千元万元,
他岁时能称为“高收入者”,
设年龄高于岁与成为高收入者没有关系
高收入者 不高收入者 合计
高于岁
不高于岁
合计
计算,
所以有的把握认为年龄与收入有关系.
17.解:,
,
若存在,使得,
只需集合在内有解,
即大于在内的最小值,
在上单减,在上单增,
所以在内的最小值为,
,解得,
所以的范围为;
由得,,,
“”是“”的充分不必要条件,
是的真子集,
分类讨论如下:
,即时,,不符题意
,即时,,
此时等号不同时成立,解得,时,满足是的真子集;
,即时,,
此时等号不同时成立,解得,时,满足是的真子集,
综上,或时,满足“”是“”的充分不必要条件.
18.解:若第一次抽奖后将球放回抽奖箱,再进行第二次抽奖,
则每次中奖的概率为,
因为两次抽奖相互独立,
所以中奖次数服从二项分布,即∽,
所以的所有可能取值为,,,则
,,
,
所以的分布列为
所以的数学期望为
若第一次抽奖后不将球放回抽奖箱,直接进行第二次抽奖,中奖次数的所有可能取值为,,,
则,
,
,
所以的分布列为
所以的数学期望为;
因为两问的数学期望相等,第问中两次奖的概率比第问的大,即
,第不中奖的概率比第问小,即,
若商场老板希望中两次奖的顾客多,产生宣传效应,则选择按第问方式进行抽.
19.解:,,,
,,,
,
同理可得:;
由知:,,
令,则,
,在上单调递增,
又,在上单调递减,在上单调递增,
,即,
故;
令,则,
由知,,所以在上单调递增,
又,
所以当时,,
当时,,
当时,,,
在点处的阶泰勒展开式为:,
,当且仅当时取等号,
当时,,当且仅当时取等号,
所以,
当时,设,,
,,
若,由于,所以,
1+x+ \dfrac{1}{2} x^{2} + \dfrac{1}{6} x^{3} + \dfrac{1}{6} x^{3} -x- \cos x" title="latexImg" />,
,从而,
若,,
所以,时,单调递减,从而,即.
综上:.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合,,则( )
A. B. C. D.
2.树人中学国旗班共有名学生,其中男女比例,平均身高,用等比例分层随机抽样的方法,从中抽取一个容量为的样本,若样本中男生的平均身高为,样本中女生人数与女生平均身高的估计值分别为( )
A. 人 B. 人 C. 人 D. 人
3.“”成立的一个充分条件可以是( )
A. B. C. D.
4.有名男生、名女生站成一排,则这名男生互不相邻的站法共有种
A. B. C. D.
5.已知,均为正实数,且,则的最小值为( )
A. B. C. D.
6.甲、乙、丙三人相互做传球训练,第次由甲将球传出,每次传球时,传球者都等可能地将球传给另外两个人中的任何一人,经过次传球后,球恰好在甲手中的概率为( )
A. B. C. D.
7.设,不等式在上恒成立,则的最大值为( )
A. B. C. D.
8.已知数列共有项,其中,且对每个,都有,则满足上述条件的数列一共有个。
A. B. C. D.
二、多选题:本题共3小题,共15分。在每小题给出的选项中,有多项符合题目要求。
9.下列命题中,正确的有( )
A. 若随机变量X~B(5,),则D(X)=
B. 若随机变量X~N(5,),且P(3X5)=0.3,则P(X7)=0.2
C. 若10件产品中有4件次品和6件正品.现从中随机抽取3件产品,记取得的次品数为随机变量X,无论是有放回的抽取还是无放回的抽取,D(X)相等
D. 从2,4,5,7,9,11,13,15,17,19中任取一个数,这个数比a大的概率为,若a恰为以上数据的第m百分位数,则m的值可能是60
10.袋中装有张相同的卡片,分别标有数字,,,,,从中有放回地随机取两次,每次取张卡片表示事件“第一次取出的卡片数字是奇数”,表示事件“第二次取出的卡片数字是偶数”,表示事件“两次取出的卡片数字之和是”,则( )
A. B. C. 与相互独立 D.
11.设,,,则下列结论中正确的是( )
A.
B. 若,,则
C. 当,时,
D. 当时,
三、填空题:本题共3小题,每小题5分,共15分。
12.已知不等式的解集为,则不等式的解集为 .
13.年月日至日“一节一赛”水上运动大赛在重庆彭水举行,甲、乙、丙、丁、戊名志愿者承担调度服务、安检服务、驾驶服务个项目志愿服务,每名志愿者需承担项工作,每项工作至少需要名志愿者,甲不承担驾驶服务,则不同的安排方法有 种用数字作答
14.已知函数的图像在其中为自然对数的底数处的切线斜率为若,且对任意恒成立,则的最大值为 .
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知函数.
讨论函数的单调性
若函数的图象是曲线,直线与曲线相切于点求函数在区间上的最大值和最小值.
16.本小题分
某从业者绘制了他在岁岁年年之间各年的月平均收入单位:千元的散点图:
由散点图知,可用经验回归方程拟合月平均收入与年龄代码的关系,试根据附注中提供的有关数据求出所选经验回归方程
若把月收入不低于万元称为“高收入者”试利用的结果,估计他岁时能否称为“高收入者”
给定以下列联表的数据,依据的独立性检验,能否认为年龄高于岁与成为高收入者有关系
为高收入者 不为高收入者
高于岁
不高于岁
附注:
参考数据:,,,,,,,其中,取,
参考公式:经验回归直线中斜率和截距的最小二乘估计分别为:,
,其中
17.本小题分
已知集合,集合.
若存在,使得,求的取值范围
若“”是“”的充分不必要条件,求实数的取值范围.
18.本小题分
某商场为了回馈广大顾客,设计了一个抽奖活动,在抽奖箱中放个大小相同的小球,其中个为红色,个为白色抽奖方式为:每名顾客进行两次抽奖,每次抽奖从抽奖箱中一次性摸出两个小球如果每次抽奖摸出的两个小球颜色相同即为中奖,两个小球颜色不同即为不中奖.
若规定第一次抽奖后将球放回抽奖箱,再进行第二次抽奖,求中奖次数的分布列和数学期望.
若规定第一次抽奖后不将球放回抽奖箱,直接进行第二次抽奖,求中奖次数的分布列和数学期望.
如果你是商场老板,如何在上述问两种抽奖方式中进行选择请写出你的选择及简要理由.
19.本小题分
给出以下三个材料:
若函数的导数为,的导数叫做的二阶导数,记作类似地,二阶导数的导数叫做的三阶导数,记作,三阶导数的导数叫做的四阶导数,一般地,阶导数的导数叫做的阶导数,即,
若,定义
若函数在包含的某个开区间上具有阶的导数,那么对于有,我们将称为函数在点处的阶泰勒展开式例如,在点处的阶泰勒展开式为根据以上三段材料,完成下面的题目:
若,在点处的阶泰勒展开式分别为,,求出,
比较中与的大小
证明:.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.或
13.
14.
15.解:,
当时,恒成立且不恒为,所有在上单调递增;
当时,令,解得或者,
所以在和上单调递增,
令,解得,
所以在上单调递减,
综上:当时,在上单调递增
当时,在和上单调递增,在上单调递减;
函数的图象是曲线,直线与曲线相切于点,
,,,即,
,
令,解得,
在上单调递减,
故在上的最大值为,最小值为.
16.解:令,则,
则,
;
,
,
回归方程为;
把带入千元万元,
他岁时能称为“高收入者”,
设年龄高于岁与成为高收入者没有关系
高收入者 不高收入者 合计
高于岁
不高于岁
合计
计算,
所以有的把握认为年龄与收入有关系.
17.解:,
,
若存在,使得,
只需集合在内有解,
即大于在内的最小值,
在上单减,在上单增,
所以在内的最小值为,
,解得,
所以的范围为;
由得,,,
“”是“”的充分不必要条件,
是的真子集,
分类讨论如下:
,即时,,不符题意
,即时,,
此时等号不同时成立,解得,时,满足是的真子集;
,即时,,
此时等号不同时成立,解得,时,满足是的真子集,
综上,或时,满足“”是“”的充分不必要条件.
18.解:若第一次抽奖后将球放回抽奖箱,再进行第二次抽奖,
则每次中奖的概率为,
因为两次抽奖相互独立,
所以中奖次数服从二项分布,即∽,
所以的所有可能取值为,,,则
,,
,
所以的分布列为
所以的数学期望为
若第一次抽奖后不将球放回抽奖箱,直接进行第二次抽奖,中奖次数的所有可能取值为,,,
则,
,
,
所以的分布列为
所以的数学期望为;
因为两问的数学期望相等,第问中两次奖的概率比第问的大,即
,第不中奖的概率比第问小,即,
若商场老板希望中两次奖的顾客多,产生宣传效应,则选择按第问方式进行抽.
19.解:,,,
,,,
,
同理可得:;
由知:,,
令,则,
,在上单调递增,
又,在上单调递减,在上单调递增,
,即,
故;
令,则,
由知,,所以在上单调递增,
又,
所以当时,,
当时,,
当时,,,
在点处的阶泰勒展开式为:,
,当且仅当时取等号,
当时,,当且仅当时取等号,
所以,
当时,设,,
,,
若,由于,所以,
1+x+ \dfrac{1}{2} x^{2} + \dfrac{1}{6} x^{3} + \dfrac{1}{6} x^{3} -x- \cos x" title="latexImg" />,
,从而,
若,,
所以,时,单调递减,从而,即.
综上:.
第1页,共1页
同课章节目录
