1-3 第1课时 集合的并集与交集运算 课件(共45张PPT)人教A版(2019)高中数学必修第一册
文档属性
| 名称 | 1-3 第1课时 集合的并集与交集运算 课件(共45张PPT)人教A版(2019)高中数学必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 521.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-05 00:00:00 | ||
图片预览











文档简介
(共45张PPT)
人教A 版(2019)高中数学必修第一册
第一章
集合与常用逻辑用语
1.3 集合的基本运算
第1课时 集合的并集与交集运算
学习目标
1. 理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集.2.能使用
Venn图或数轴表达集合的关系及运算.
自主阅读·新知预习
文字语 言
一般地,由 所有 属于集合A或属于集合B的元素组成的集合,称为集合
A与B的 并集,记作AUB (读作“ A并B ”)
符号语 言
A JB=
图形语 言
性质
AUB=BUA,AUA=A,AUo=A,AUB=A BSA,ASAUB.
知识点1 并集
[巧梳理]
{x|x∈A,或x∈B}
[微体验]
1. 设集合A={x|1≤x≤3},B={x|2A.{x|2C.{x|1≤x<4} D.{x|1解析:C AUB={x|1≤x≤3}U{x|2文字
语言 一般地, 由 所有 属于集合A且属于集合B的元素组成的集合,称为 集合A与B的 交集 ,记作 A∩B (读作“ 交B ”)
符号语言 A∩B= A, B}
图形语言 AC
④ B
性质 A∩B=B∩A,A∩A=A,A∩0=0,A∩B=A ASB,A∩BEAUB, A∩BCA,A∩BSB.
知识点2 交集
[巧梳理]
[微点拨]
(1)A∩B仍是一个集合;(2)文字语言中“所有”的含义: A∩B中任一元素都是A与B 的
公共元素,A与B的公共元素都属于A∩B;(3) 如果两个集合没有公共元素,不能说两个集 合没有交集,而是A∩B=0
[微体验]
2.设集合A={1,3,5,7},B={x|2≤x≤5}, 则ANB=(B)
A.{1,3} B.{3,5}
C.{5,7} D.{1,7}
解析:B 因为A={1,3,5,7},B={x|2≤x≤5}, 所 以A∩B={3,5}.
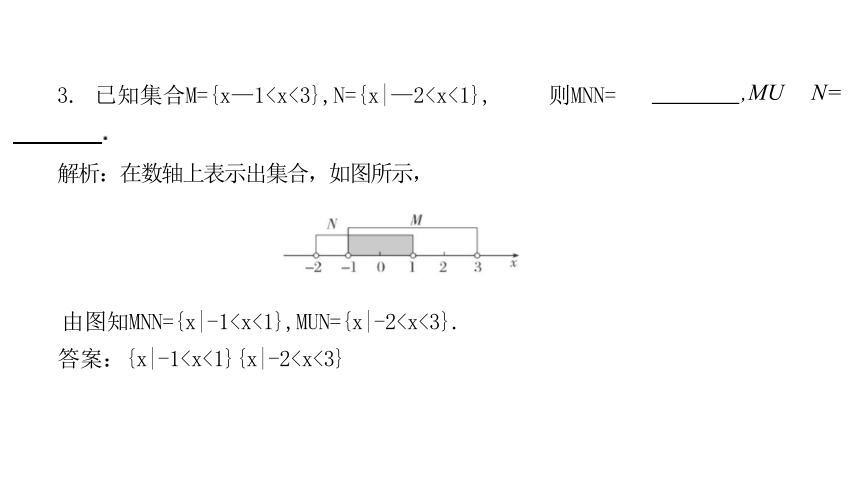
由图知MNN={x|-1答案:{x|-13. 已知集合M={x—1解析:在数轴上表示出集合,如图所示,
,MU N=
合作探究·深化提能
学习任务一并集的运算
[例1](链接教材P 0例1、例2)(1)已知集合 则
AUB=(C)
A.{1} B.{-1,1,3}
C.{-3,—1,1} D.{-3,—1,1,3}
(2)已知集合M={x|-35}, 则MUN=(A )
A.{x|x<-5 或x>-3}
B.{x|-5C.{x|-3D.{x|x<-3 或x>5}
解析:(1)A={-3,1},B={-1,1},
则AUB={-3,-1,1}, 故选C.
(2)在数轴上表示集合M,N, 可知MUN={x|x<-5 或x>-3}. 故选A.
方法技巧
求集合并集的两种基本方法
(1)定义法:若集合是用列举法表示的,可以直接利用并集的定义求解;
(2)数形结合法:若集合是用描述法表示的由实数组成的数集,则可以借助数轴分析
求解.
[跟踪训练]
1.(多选)满足{1,3}UA={1,3,5} 的集合A可能是(AB)
A.{5} B.{1,5}
C.{3} D.{1,3}
解析: AB 由{1,3}UA={1,3,5} 知,AS{1,3,5}, 且A中至少有1个元素5.
学习任务二交集的运算
[例2](链接教材P 1例3)(1)设集合A={x|-1≤x≤2},B={x|O≤x≤4}, 则ANB等于
(A)
A.{x|O≤x≤2} B.{x|1≤x≤2}
C.{x|O≤x≤4} D.{x|1≤x≤4}
(2)已知集合A={x|x=3n+2,n∈N},B={6,8,10,12,14},
的个数为(D)
A.5 B.4
C.3 D.2
则集合ANB中元素
则由交集的定义得,A∩B={x|O≤x≤2}.
(2)集合A中元素满足x=3n+2,n∈N, 即被3除余2,而集合B中满足这一要求的元素
只有8和14.故选D.
解析:(1)在数轴上表示出集合A与B, 如图.
方法技巧
求两集合交集的方法
(1)对于元素个数有限的集合,逐个挑出两个集合的公共元素即可;
(2)对于元素个数无限的集合, 一般借助数轴求交集,两个集合的交集等于两个集合
在数轴上的相应图形所覆盖的公共范围,要注意端点值的取舍.
[跟踪训练]
2.已知集合A={x|25}, 则A∩B=(C)
A.{x|25}
C.{x|25} 解析:C 集合A、B画在数轴上,如图,
由图可知A∩B={x|23.(多选)已知集合M={x|-2≤x-1≤2} 和N={x|x=2k-1,k∈N*} 关系的Venn图如图
所示,则阴影部分表示的集合中的元素有(CD)
B.0
D.3
∵M={x|-1≤x≤3},N={x|x=2k-1,k∈N*},∴MNN={1,3},故
A.—1
C.1
解析: CD
选CD.
学习任务三交集、并集性质的应用
[例3]已知集合A={x|x≤-1 或x≥3},B={x|a范围是(C)
A.3≤a<4 B.—1C.a≤—1 D.a<—1
解析:C 利用数轴,若AUB=R, 则 a≤-1.
[发散思维]
1.(变条件)把例题中AUB=R, 变 成AUB=A, 求实数a的取值范围.
解:当a≥4 时,集合B为空集,满足题意;当a<4时,若要满足AUB=A, 必有a≥3.
综上实数a 的取值范围是a≥3.
2.(变条件)把例题中集合B变为B={xa数a的取值范围.
解:当a≥2 时,集合B为空集,满足题意;当a<2时,则有a≥-1 且4-a<3, 故有
11.
■方法技巧
利用集合间的关系求参数的一般步骤
(1)若集合能一一列举,则用观察法得到不同集合中元素之间的关系;与不等式有关
的集合,利用数轴得到不同集合间的关系.
(2)将集合之间的关系转化为方程或不等式是否有解或解集的取值范围.
(3)解方程(组)或不等式(组),从而确定参数的值或取值范围.
随堂检测·内化素养
1.若集合A={x|0A.{x|0C.{x|0∴A∩B={x|02.满足{2,4}UA={2,4,6} 的所有集合A的个数是(D)
A.1 B.2
C.3 D.4
解析:D 由{2,4}UA={2,4,6}, 知AE{2,4,6} 且A中至少有一个元素为6,
它们分别是{6},{2,6},{4,6},{2,4,6}.
3.若集合A,B,C 满足A∩B=A,BUC=C, 则 A与C一定满足( c )
A.A C B.C A
C.ACC D.CCA
解析:C A∩B=A ASB,BUC=C BSC,所 以ASC.
4 . 已知A={x|2(1)若A∩B={x|3(2)若AUB={x|2答案:(1)3(2){a|2≤a<4}
课时作业·分层自检
基础巩固练
1. 已知集合M={0,1,3},N={x|x=3a,a∈M}, 则MUN等于( D )
A.{0} B.{0,3}
C.{1,3,9} D.{0,1,3,9}
解析:D 易知N={0,3,9}, 故MUN={0,1,3,9}.
1 2 3 4 5 6 7 8 9 10 11 12 13 14
2.设集合A={x|-2≤x≤3},B={x|-1≤x≤4}, 则A∩B等于(A)
A.{x|-1≤x≤3} B.{x|-1≤x≤4}
C.{x|3≤x≤4} D.{x|-2≤x≤4}
解析:A 在数轴上表示出集合A与B, 如图所示.
则由交集的定义,知A∩B={x|-1≤x≤3}.
12 3 4 5 6 7 8 9 10 11 12 13 14
3.设集合A={1,2,6},B={2,4},C={x-1≤x≤5}, 则(AUB)NC等于(B)
A.{2} B.{1,2,4}
C.{1,2,4,6} D.{x∈R|-1≤x≤5}
解析:B (AUB)NC={1,2,4,6}∩C={1,2,4}.
1 23 4 5 6 7 8 9 10 11 12 13 14
4. 已知集合M={-1,1}, 则满足MUN={-1,1,2} 的集合N的个数是(D)
A.1 B.2
C.3 D.4
解析:D 依题意,得满足MUN={-1,1,2} 的集合N有{2},{-1,2},{1,
2},{- 1,1,2},共4个.
1 2 3 4 5 6 7 8 9 10 11 12 13 14
5.(多选)已知集合A={x|x =x}, 集合B中有两个元素,且满足AUB={0,1,2},
则集合B可以是(BD)
A.{0,1} B.{0,2}
C.{0,3} D.{1,2}
解析: BD 由题意知,集合A={0,1}, 因为B中有两个元素,且AUB={0,1,
2},所以B 可以为{0,2},{1,2}.故选BD.
1 2 3 4 5 6 7 8 9 10 11 12 13 14
解析:AD 因为A={1,3,√m},B={1,m}, 所以m≠1,m≠9. 因为AUB=A, 所以BSA, 所以m=3 或m=√m, 即m=3或m=0或m=1(舍去),所以m=0或m=3, 故选AD.
6.(多选)已知集合A={1,3,√m},B={1,m}, 若AUB=A,则m的值可以等于(AD)
1 2 3 4 5 6 7 8 9 10 11 12 13 14
A.0
C.3
B.1
D.3
解析:因为 ,B={x∈Z|x≤2}, 所 以
所以A∩B={0,1,2}.
答案:{0,1,2}
7. 已知集合 ,B={x∈Zx≤2}, 则 A∩B=
1 2 3 4 5 6 7 8 9 10 11 12 13 14
解析:因为A∩B={2}, 所 以 2a=2, 即 a=1. 所以b=2, 所 以A={3,2},B={1,
2},所以AUB={1,2,3}.
答案:{1,2,3}
8. 已知集合A={3,2a},B={a,b}. 若A∩B={2}, 则AUB= ·
1 2 3 4 5 6 7 8 9 10 11 12 13 14
9. 已知集合A={x|x≥3},B={x|1≤x≤7},C={x|x≥a-1}.
(1)求A∩B,AUB;
(2)若CUA=A, 求实数a 的取值范围.
解:(1)因为A={x|x≥3},B={x|1≤x≤7}, 所 以A∩B={x| ≤x≤7},AUB=
{x|x≥1}.
(2)因为CUA=A,A={x|x≥3},C={x|x≥a-1},
所以CEA, 所以a-1≥3, 即a≥4.
1 2 3 4 5 6 7 8 9 10 11 12 13 14
综合应用练
10.已知集合A={1,2},B={xmx—1=0}, 若 ANB=B, 则符合条件的实数 m 的
解析:C 当m=0
1i 即m=1 或
要使A∩B=B, 则
时 ,B=0,A∩B=B; 当m≠0 时,
值组成的集合为(C)
1 2 3 4 5 6 7 8 910 11 12 13 14
A.{m|-3≤m≤4} B.{m|-3C.{m|2解析:ACD 因为AUB=A, 所 以BSA.① 若B 不为空集,则m+1<2m-1, 解得m>2.
因为A={x|-2≤x≤7},B={x|m+13≤m≤4.此时2实数m满足m≤4 即可.故选ACD.
11.(多选)已知集合A={x|-2≤x≤7},B={xm+1数m 的取值范围可以是(ACD)
则使AUB=A 的实
1 2 3 4 5 6 7 8 9 10 ll 12 13 14
12.已知集合A={x|x —px-2=0},B={x|x +qx+r=0}, 且AUB={-2,1,5},
A∩B={-2}, 则p+q+r 等于(C)
A.12 B.6
C.—14 D.—12
解析: C 因为A∩B={-2},
所以-2∈A且 - 2∈B, 将x=-2 代入x -px-2=0,
得p=-1,
所以A={1,-2},
因为AUB={-2,1,5},A∩B={-2},
所以B={-2,5},
所以q=-[(-2)+5]=-3,r=(-2)×5=-10,
所以p+q+r=-14.
1 2 3 4 5 6 7 8 9 10 11 12 13 14
13. 设集合M={x|-4取值范围为
解析:由MNN=N, 得 NSM,
故当N=0, 即 t+2≥2t—1,t≤3 时 ,M∩N=N 成立;
当N≠ 时,由图 无解.
综上可知,所求实数t 的取值范围为{1|t≤3}.
答案:{t|t≤3}
t+2 2t-l 3 X
1 2 3 4 5 6 7 8 9 10 11 12 13 14
探索创新练
14. 设集合A={2,—1,x —x+1},B={2y,-4,x+4},C={-1,7}
C, 求实数x,y 的值及AUB.
解:由A={2,-1,x -x+1},B={2y,-4,x+4},C={-1,7}
得
7∈A,7∈B 且 - 1∈B,
所以在集合A中x -x+1=7,
解得x=-2 或x=3.
当x=-2 时,在集合B中 ,x+4=2,
又2∈A, 故2∈(A∩B)=C,
1 2 3 4 5 6 7 8 9 10 11 12 1314
且A∩B=
且A∩B=C,
但24C, 故 x=—2 不符合题意,舍去.
当x=3 时,在集合B 中 ,x +4=7,
所以2y=—1, 解 得 符合题意,
所 以A={2,—1,7},B={-1,-4,7},
所 以AUB={2,—1,7,-4}.
1 2 3 4 5 6 7 8 9 10 11 12 1314
本部分内容讲解结束
人教A 版(2019)高中数学必修第一册
第一章
集合与常用逻辑用语
1.3 集合的基本运算
第1课时 集合的并集与交集运算
学习目标
1. 理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集.2.能使用
Venn图或数轴表达集合的关系及运算.
自主阅读·新知预习
文字语 言
一般地,由 所有 属于集合A或属于集合B的元素组成的集合,称为集合
A与B的 并集,记作AUB (读作“ A并B ”)
符号语 言
A JB=
图形语 言
性质
AUB=BUA,AUA=A,AUo=A,AUB=A BSA,ASAUB.
知识点1 并集
[巧梳理]
{x|x∈A,或x∈B}
[微体验]
1. 设集合A={x|1≤x≤3},B={x|2
语言 一般地, 由 所有 属于集合A且属于集合B的元素组成的集合,称为 集合A与B的 交集 ,记作 A∩B (读作“ 交B ”)
符号语言 A∩B= A, B}
图形语言 AC
④ B
性质 A∩B=B∩A,A∩A=A,A∩0=0,A∩B=A ASB,A∩BEAUB, A∩BCA,A∩BSB.
知识点2 交集
[巧梳理]
[微点拨]
(1)A∩B仍是一个集合;(2)文字语言中“所有”的含义: A∩B中任一元素都是A与B 的
公共元素,A与B的公共元素都属于A∩B;(3) 如果两个集合没有公共元素,不能说两个集 合没有交集,而是A∩B=0
[微体验]
2.设集合A={1,3,5,7},B={x|2≤x≤5}, 则ANB=(B)
A.{1,3} B.{3,5}
C.{5,7} D.{1,7}
解析:B 因为A={1,3,5,7},B={x|2≤x≤5}, 所 以A∩B={3,5}.
由图知MNN={x|-1
,MU N=
合作探究·深化提能
学习任务一并集的运算
[例1](链接教材P 0例1、例2)(1)已知集合 则
AUB=(C)
A.{1} B.{-1,1,3}
C.{-3,—1,1} D.{-3,—1,1,3}
(2)已知集合M={x|-3
A.{x|x<-5 或x>-3}
B.{x|-5
解析:(1)A={-3,1},B={-1,1},
则AUB={-3,-1,1}, 故选C.
(2)在数轴上表示集合M,N, 可知MUN={x|x<-5 或x>-3}. 故选A.
方法技巧
求集合并集的两种基本方法
(1)定义法:若集合是用列举法表示的,可以直接利用并集的定义求解;
(2)数形结合法:若集合是用描述法表示的由实数组成的数集,则可以借助数轴分析
求解.
[跟踪训练]
1.(多选)满足{1,3}UA={1,3,5} 的集合A可能是(AB)
A.{5} B.{1,5}
C.{3} D.{1,3}
解析: AB 由{1,3}UA={1,3,5} 知,AS{1,3,5}, 且A中至少有1个元素5.
学习任务二交集的运算
[例2](链接教材P 1例3)(1)设集合A={x|-1≤x≤2},B={x|O≤x≤4}, 则ANB等于
(A)
A.{x|O≤x≤2} B.{x|1≤x≤2}
C.{x|O≤x≤4} D.{x|1≤x≤4}
(2)已知集合A={x|x=3n+2,n∈N},B={6,8,10,12,14},
的个数为(D)
A.5 B.4
C.3 D.2
则集合ANB中元素
则由交集的定义得,A∩B={x|O≤x≤2}.
(2)集合A中元素满足x=3n+2,n∈N, 即被3除余2,而集合B中满足这一要求的元素
只有8和14.故选D.
解析:(1)在数轴上表示出集合A与B, 如图.
方法技巧
求两集合交集的方法
(1)对于元素个数有限的集合,逐个挑出两个集合的公共元素即可;
(2)对于元素个数无限的集合, 一般借助数轴求交集,两个集合的交集等于两个集合
在数轴上的相应图形所覆盖的公共范围,要注意端点值的取舍.
[跟踪训练]
2.已知集合A={x|2
A.{x|2
C.{x|2
由图可知A∩B={x|2
所示,则阴影部分表示的集合中的元素有(CD)
B.0
D.3
∵M={x|-1≤x≤3},N={x|x=2k-1,k∈N*},∴MNN={1,3},故
A.—1
C.1
解析: CD
选CD.
学习任务三交集、并集性质的应用
[例3]已知集合A={x|x≤-1 或x≥3},B={x|a
A.3≤a<4 B.—1
解析:C 利用数轴,若AUB=R, 则 a≤-1.
[发散思维]
1.(变条件)把例题中AUB=R, 变 成AUB=A, 求实数a的取值范围.
解:当a≥4 时,集合B为空集,满足题意;当a<4时,若要满足AUB=A, 必有a≥3.
综上实数a 的取值范围是a≥3.
2.(变条件)把例题中集合B变为B={xa
解:当a≥2 时,集合B为空集,满足题意;当a<2时,则有a≥-1 且4-a<3, 故有
1
■方法技巧
利用集合间的关系求参数的一般步骤
(1)若集合能一一列举,则用观察法得到不同集合中元素之间的关系;与不等式有关
的集合,利用数轴得到不同集合间的关系.
(2)将集合之间的关系转化为方程或不等式是否有解或解集的取值范围.
(3)解方程(组)或不等式(组),从而确定参数的值或取值范围.
随堂检测·内化素养
1.若集合A={x|0
A.1 B.2
C.3 D.4
解析:D 由{2,4}UA={2,4,6}, 知AE{2,4,6} 且A中至少有一个元素为6,
它们分别是{6},{2,6},{4,6},{2,4,6}.
3.若集合A,B,C 满足A∩B=A,BUC=C, 则 A与C一定满足( c )
A.A C B.C A
C.ACC D.CCA
解析:C A∩B=A ASB,BUC=C BSC,所 以ASC.
4 . 已知A={x|2
课时作业·分层自检
基础巩固练
1. 已知集合M={0,1,3},N={x|x=3a,a∈M}, 则MUN等于( D )
A.{0} B.{0,3}
C.{1,3,9} D.{0,1,3,9}
解析:D 易知N={0,3,9}, 故MUN={0,1,3,9}.
1 2 3 4 5 6 7 8 9 10 11 12 13 14
2.设集合A={x|-2≤x≤3},B={x|-1≤x≤4}, 则A∩B等于(A)
A.{x|-1≤x≤3} B.{x|-1≤x≤4}
C.{x|3≤x≤4} D.{x|-2≤x≤4}
解析:A 在数轴上表示出集合A与B, 如图所示.
则由交集的定义,知A∩B={x|-1≤x≤3}.
12 3 4 5 6 7 8 9 10 11 12 13 14
3.设集合A={1,2,6},B={2,4},C={x-1≤x≤5}, 则(AUB)NC等于(B)
A.{2} B.{1,2,4}
C.{1,2,4,6} D.{x∈R|-1≤x≤5}
解析:B (AUB)NC={1,2,4,6}∩C={1,2,4}.
1 23 4 5 6 7 8 9 10 11 12 13 14
4. 已知集合M={-1,1}, 则满足MUN={-1,1,2} 的集合N的个数是(D)
A.1 B.2
C.3 D.4
解析:D 依题意,得满足MUN={-1,1,2} 的集合N有{2},{-1,2},{1,
2},{- 1,1,2},共4个.
1 2 3 4 5 6 7 8 9 10 11 12 13 14
5.(多选)已知集合A={x|x =x}, 集合B中有两个元素,且满足AUB={0,1,2},
则集合B可以是(BD)
A.{0,1} B.{0,2}
C.{0,3} D.{1,2}
解析: BD 由题意知,集合A={0,1}, 因为B中有两个元素,且AUB={0,1,
2},所以B 可以为{0,2},{1,2}.故选BD.
1 2 3 4 5 6 7 8 9 10 11 12 13 14
解析:AD 因为A={1,3,√m},B={1,m}, 所以m≠1,m≠9. 因为AUB=A, 所以BSA, 所以m=3 或m=√m, 即m=3或m=0或m=1(舍去),所以m=0或m=3, 故选AD.
6.(多选)已知集合A={1,3,√m},B={1,m}, 若AUB=A,则m的值可以等于(AD)
1 2 3 4 5 6 7 8 9 10 11 12 13 14
A.0
C.3
B.1
D.3
解析:因为 ,B={x∈Z|x≤2}, 所 以
所以A∩B={0,1,2}.
答案:{0,1,2}
7. 已知集合 ,B={x∈Zx≤2}, 则 A∩B=
1 2 3 4 5 6 7 8 9 10 11 12 13 14
解析:因为A∩B={2}, 所 以 2a=2, 即 a=1. 所以b=2, 所 以A={3,2},B={1,
2},所以AUB={1,2,3}.
答案:{1,2,3}
8. 已知集合A={3,2a},B={a,b}. 若A∩B={2}, 则AUB= ·
1 2 3 4 5 6 7 8 9 10 11 12 13 14
9. 已知集合A={x|x≥3},B={x|1≤x≤7},C={x|x≥a-1}.
(1)求A∩B,AUB;
(2)若CUA=A, 求实数a 的取值范围.
解:(1)因为A={x|x≥3},B={x|1≤x≤7}, 所 以A∩B={x| ≤x≤7},AUB=
{x|x≥1}.
(2)因为CUA=A,A={x|x≥3},C={x|x≥a-1},
所以CEA, 所以a-1≥3, 即a≥4.
1 2 3 4 5 6 7 8 9 10 11 12 13 14
综合应用练
10.已知集合A={1,2},B={xmx—1=0}, 若 ANB=B, 则符合条件的实数 m 的
解析:C 当m=0
1i 即m=1 或
要使A∩B=B, 则
时 ,B=0,A∩B=B; 当m≠0 时,
值组成的集合为(C)
1 2 3 4 5 6 7 8 910 11 12 13 14
A.{m|-3≤m≤4} B.{m|-3
因为A={x|-2≤x≤7},B={x|m+1
11.(多选)已知集合A={x|-2≤x≤7},B={xm+1
则使AUB=A 的实
1 2 3 4 5 6 7 8 9 10 ll 12 13 14
12.已知集合A={x|x —px-2=0},B={x|x +qx+r=0}, 且AUB={-2,1,5},
A∩B={-2}, 则p+q+r 等于(C)
A.12 B.6
C.—14 D.—12
解析: C 因为A∩B={-2},
所以-2∈A且 - 2∈B, 将x=-2 代入x -px-2=0,
得p=-1,
所以A={1,-2},
因为AUB={-2,1,5},A∩B={-2},
所以B={-2,5},
所以q=-[(-2)+5]=-3,r=(-2)×5=-10,
所以p+q+r=-14.
1 2 3 4 5 6 7 8 9 10 11 12 13 14
13. 设集合M={x|-4
解析:由MNN=N, 得 NSM,
故当N=0, 即 t+2≥2t—1,t≤3 时 ,M∩N=N 成立;
当N≠ 时,由图 无解.
综上可知,所求实数t 的取值范围为{1|t≤3}.
答案:{t|t≤3}
t+2 2t-l 3 X
1 2 3 4 5 6 7 8 9 10 11 12 13 14
探索创新练
14. 设集合A={2,—1,x —x+1},B={2y,-4,x+4},C={-1,7}
C, 求实数x,y 的值及AUB.
解:由A={2,-1,x -x+1},B={2y,-4,x+4},C={-1,7}
得
7∈A,7∈B 且 - 1∈B,
所以在集合A中x -x+1=7,
解得x=-2 或x=3.
当x=-2 时,在集合B中 ,x+4=2,
又2∈A, 故2∈(A∩B)=C,
1 2 3 4 5 6 7 8 9 10 11 12 1314
且A∩B=
且A∩B=C,
但24C, 故 x=—2 不符合题意,舍去.
当x=3 时,在集合B 中 ,x +4=7,
所以2y=—1, 解 得 符合题意,
所 以A={2,—1,7},B={-1,-4,7},
所 以AUB={2,—1,7,-4}.
1 2 3 4 5 6 7 8 9 10 11 12 1314
本部分内容讲解结束
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
