2.1等式性质与不等式性质(第二课时)(共17张PPT)-(新教材)人教A版(2019)高中数学必修第一册课件
文档属性
| 名称 | 2.1等式性质与不等式性质(第二课时)(共17张PPT)-(新教材)人教A版(2019)高中数学必修第一册课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 1015.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-05 17:55:35 | ||
图片预览




文档简介
(共17张PPT)
2.1等式性质与不等式性质(第二课时
立德树人和谐发展
等式性质 不等式性质
现实世界
相等关系
不等关系
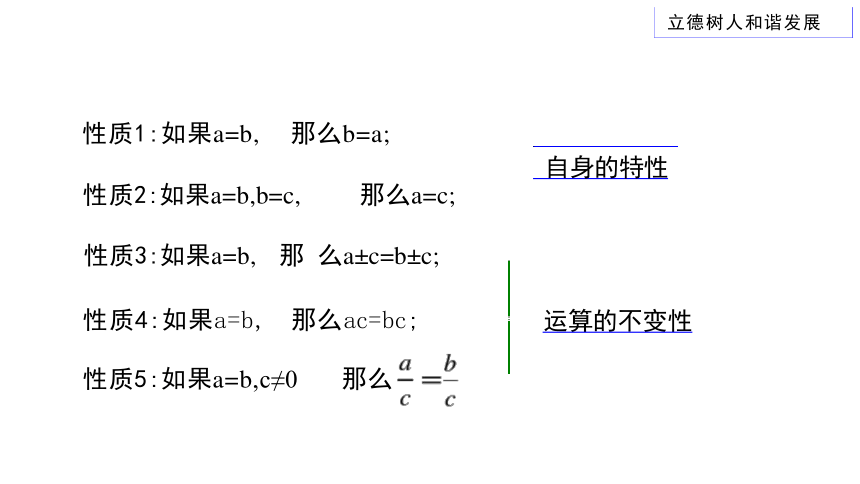
性质1:如果a=b, 那么b=a;
性质2:如果a=b,b=c, 那么a=c;
性质3:如果a=b, 那 么a±c=b±c;
性质4:如果a=b, 那么ac=bc;
性质5:如果a=b,c≠0 那么
立德树人和谐发展
运算的不变性
自身的特性
性质2:如果a>b,b>c, 那么 C;
性质3:如果a>b, 那么a+c>b+c;
性质4:如果a>b, 那么ac>bc;
性质5:如果a>b,c≠0, 那么
问题类比等式的性质,你能猜想不等式的性质吗 写出
你的猜想.
性质1:如果a>b, 那 么b运算的不变性
思考:这些结论正确吗
立德树人和谐发展
自身的特性
等式
不等式
对称性 a=b b=a
Q
传递性 a= ), =C 二a=C
立德树人和谐发展
探究
类比等式的基本性质,你能猜想不等式的基本 性质吗,并加以证明吗
立德树人和谐发展
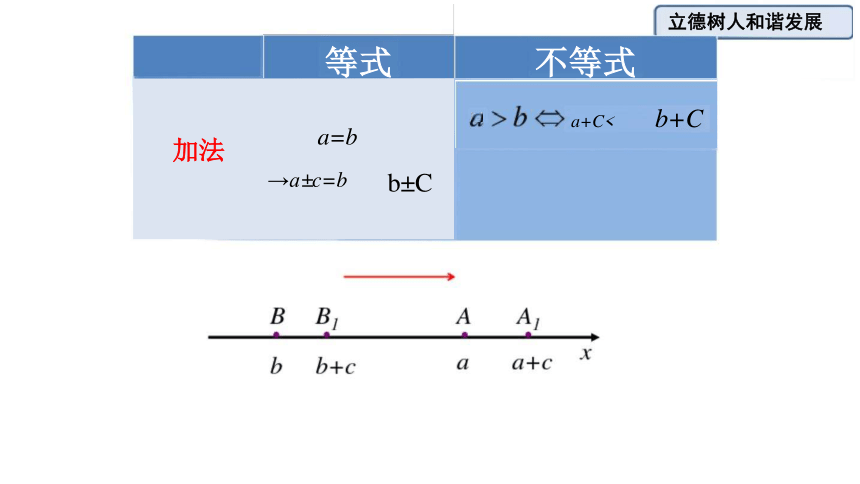
等式 不等式
a+C< b+C
a=b
→a±c=b
加法
b±C
立德树人和谐发展
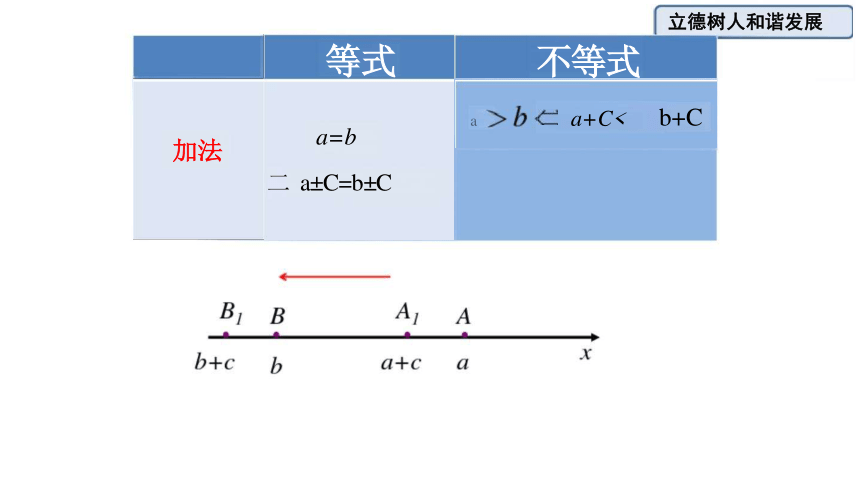
不等式
等式
a=b
二 a±C=b±C
a a+C< b+C
加法
立德树人和谐发展
等式 不等式
加法 a=b →a±c=b±C a+C十 C
等式 不等式
a=
乘法 a
立德树人和谐发展
运算的不变性,规律性
性质1:如果a>b, 那么b性质2:如果a>b,b>c, 那么a>c;
性质3:如果a>b, 那么a+c>b+c;
性质4:如果a>b,c>0, 那么ac>bc ,如果a>b,c<0,
性质5:如果a>b,c>d, 那么a+c>b+d;
性质6:如果a>b>0,c>d>0, 那么ac>bd;
性质7:如果a>b>0, 那么a">bn(n∈N*,n≥2).
立德树人和谐发展
那么ac证明:∵a>b>0,
于是
又由c<0, 得
∴ab>0,
即
例1 已知a>b>0,c<0, 求证:
立德树人和谐发展
用不等号“>”或“<”填空
(1)如果a>b,c(2)如果a>b>0,c(3)如果a>b>0,那么
(4)如果a>b>c>0,那
练习
立德树人和谐发展
立德树人和谐发展
练习
用不等号“>”或“<”填空
(1)如果a>b,c _b-d
(2)如果a>b>0,c(3)如果a>b>0,那么<
(4)如果a>b>c>0,那 么 <
C
b
1
立德树人和谐发展
练习
对于实数a,b,c,有下列结论:
①若a>b,则ac②若ac >bc ,则a>b;
③若aab>b ;
④若c>a>b>0,则
⑤若a>b, 则a>0,b<0.
其中正确结论的有
立德树人和谐发展
练习
对于实数a,b,c,有下列结论:
①若a>b,则ac②若ac >bc ,则a>b;
③若aab>b ;
④若c>a>b>0,则
⑤若 a>b, 则a>0,b<0.
;
其中正确结论的有 ② ③④⑤
不等式的性质
内 容
对称性
传递性
加法性质
乘法性质
指
要弄清每一性质的条件和结论,注意条件的放宽和加强,以及条件 与结论之间的相互联系.特别要注意有些性质的逆命题成立的;有 些性质的逆命题不成立
立德树人和谐发展
关于不等式性质的学习要注意
小结
作业
1、(作业B本)
课本 P42 习题2.1 第5,7,8,11,12题
2、金版 P29-P32
P30第5题 P317,8,9 P32例题2的3,5不用做,
其他的都做
3、预习 2.2基本不等式
(看书并填写金版P34的预习导学)
立德树人和谐发展
2.1等式性质与不等式性质(第二课时
立德树人和谐发展
等式性质 不等式性质
现实世界
相等关系
不等关系
性质1:如果a=b, 那么b=a;
性质2:如果a=b,b=c, 那么a=c;
性质3:如果a=b, 那 么a±c=b±c;
性质4:如果a=b, 那么ac=bc;
性质5:如果a=b,c≠0 那么
立德树人和谐发展
运算的不变性
自身的特性
性质2:如果a>b,b>c, 那么 C;
性质3:如果a>b, 那么a+c>b+c;
性质4:如果a>b, 那么ac>bc;
性质5:如果a>b,c≠0, 那么
问题类比等式的性质,你能猜想不等式的性质吗 写出
你的猜想.
性质1:如果a>b, 那 么b
思考:这些结论正确吗
立德树人和谐发展
自身的特性
等式
不等式
对称性 a=b b=a
Q
传递性 a= ), =C 二a=C
立德树人和谐发展
探究
类比等式的基本性质,你能猜想不等式的基本 性质吗,并加以证明吗
立德树人和谐发展
等式 不等式
a+C< b+C
a=b
→a±c=b
加法
b±C
立德树人和谐发展
不等式
等式
a=b
二 a±C=b±C
a a+C< b+C
加法
立德树人和谐发展
等式 不等式
加法 a=b →a±c=b±C a+C
等式 不等式
a=
乘法 a
立德树人和谐发展
运算的不变性,规律性
性质1:如果a>b, 那么b
性质3:如果a>b, 那么a+c>b+c;
性质4:如果a>b,c>0, 那么ac>bc ,如果a>b,c<0,
性质5:如果a>b,c>d, 那么a+c>b+d;
性质6:如果a>b>0,c>d>0, 那么ac>bd;
性质7:如果a>b>0, 那么a">bn(n∈N*,n≥2).
立德树人和谐发展
那么ac
于是
又由c<0, 得
∴ab>0,
即
例1 已知a>b>0,c<0, 求证:
立德树人和谐发展
用不等号“>”或“<”填空
(1)如果a>b,c
(4)如果a>b>c>0,那
练习
立德树人和谐发展
立德树人和谐发展
练习
用不等号“>”或“<”填空
(1)如果a>b,c
(2)如果a>b>0,c
(4)如果a>b>c>0,那 么 <
C
b
1
立德树人和谐发展
练习
对于实数a,b,c,有下列结论:
①若a>b,则ac
③若a
④若c>a>b>0,则
⑤若a>b, 则a>0,b<0.
其中正确结论的有
立德树人和谐发展
练习
对于实数a,b,c,有下列结论:
①若a>b,则ac
③若a
④若c>a>b>0,则
⑤若 a>b, 则a>0,b<0.
;
其中正确结论的有 ② ③④⑤
不等式的性质
内 容
对称性
传递性
加法性质
乘法性质
指
要弄清每一性质的条件和结论,注意条件的放宽和加强,以及条件 与结论之间的相互联系.特别要注意有些性质的逆命题成立的;有 些性质的逆命题不成立
立德树人和谐发展
关于不等式性质的学习要注意
小结
作业
1、(作业B本)
课本 P42 习题2.1 第5,7,8,11,12题
2、金版 P29-P32
P30第5题 P317,8,9 P32例题2的3,5不用做,
其他的都做
3、预习 2.2基本不等式
(看书并填写金版P34的预习导学)
立德树人和谐发展
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
