3.1.2函数的表示法-【新教材】人教A版(2019)高中数学必修第一册课件(共19张PPT)
文档属性
| 名称 | 3.1.2函数的表示法-【新教材】人教A版(2019)高中数学必修第一册课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-05 18:11:38 | ||
图片预览






文档简介
(共19张PPT)
新高考新教材
高中数第一册第三章函数的概念与性质
3.1.2
函数的表示法
x 叫做自变量,x 的取值范围构成的集合A叫
做函数的定义域;与x的值相对应的y值叫做函数值, 所有函数值组成的集合叫做函数的值域。
函数值的集合{f(x)lx∈A}
函数的三要素:定义域、值域、对应关系
知识回顾 设A、B是非空数集,如果对于集合A中的任意
一个数x, 按照某种确定的对应关系f, 在集合B 中都有唯一确定的数y和它对应,就称
f:A→B 为从集合A到集合B的一个函数,
记作: y=f(x),x∈A
我们初中已经接触函数几种常用的表示法
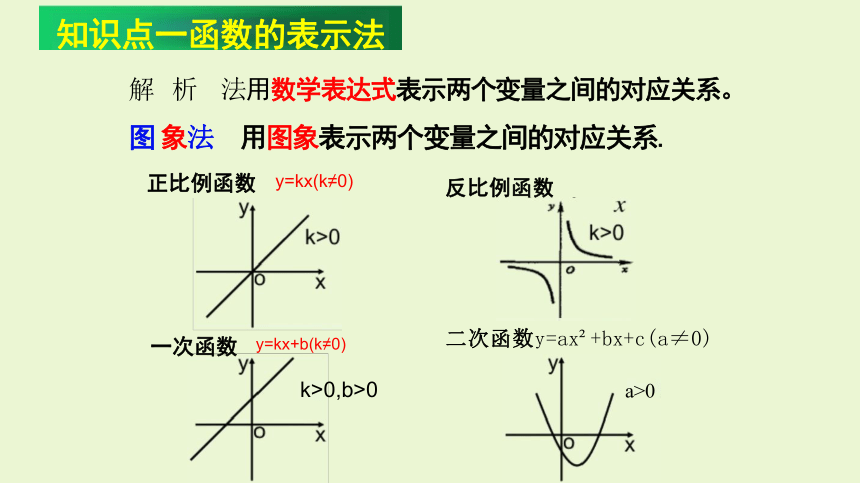
1、解析法:用数学表达式表示两个变量之间的对应关系;
2、图象法:用图象表示两个变量之间的对应关系;
3、列表法:用表格表示两个变量之间的对应关系.
正比例函数 y=kx(k≠0)
一次函数 y=kx+b(k≠0)
k>0,b>0
解 析 法用数学表达式表示两个变量之间的对应关系。
图 象法 用图象表示两个变量之间的对应关系.
a>0
知识点一函数的表示法
二次函数y=ax +bx+c(a≠0)
反比例函数
冽题讲解
【例4】某种笔记本的单价是5元,买m(m∈{1,2,3,4,5})个笔记本需要y
元.试用函数的三种表示法来表示函数y= f(m).
【图像法】函数图像可以表示如图:
【解析法】y=5m,m∈{1,2,3,4,5}
笔记本数m 1 2 3 4
5
钱数y 5 10 15 20
25
【列表法】函数可以表示如下表:
优点 缺点
联系
解 析 法 ①简明、全面地概括了变 量间的关系;②可以通过 解析式求出任意一个自变 量的值所对应的函数值; ③便于研究函数性质. 不够形象、直观、 具体,并不是所有 的函数都能用解析 法表示出来.
三种方 法之间有 时可以相 互转化, 面对实际 情景时, 我们要根 据不同的 需要选择 恰当的表 示法表示 函数 .
图 像 法 直观形象地表示出函数 的变化情况,有利于通过 图象研究函数的某些性质. 只能近似地求出 自变量的值所对应 的函数值,而且有 时误差太大.
列 表 法 不通过计算就可以直 接看出与自变量对应的 函数值. 只能表示自变量 取值较少的有限的 对应关系.
思考2
比较函数的三种表示法,它们各自的特点是什么
解:由题意得,设f(x)=ax+b(a≠0) 因为3f(x+1)-f(x)=2x+9
所以3a(x+1)+3b-ax-b=2x+9 由等式的性质得
例1已知f(x) 一次函数,且满足3f(x+1)-f(x)=2x+9, 求函数
f(x) 解析式。
解得a=1,b=3
所以所求函数解析式为f(x)=x+3
知识点二求函数的解析式
待定系数法
知识点二求函数的解析式
例 2 若f(2x+1)=6x+5, 求函数f(x) 解析式
设2x+1=t,
所以f(t)=6
所以f(x)=3x+2
换元法
国
知识点二求函数的解析式
例 3 若f(x)+2f(-x)=x +2x,
f(x)+2f(-x)=x2+2x
令x=-x得
f(-x)+2f
联立两式
得
求函数f(x) 解析式
方程的思想
1求下列函数的解析式:
(1)已知函数f(x+1)=x+2 √x, 求f(x);
(2)已知函数f(x)是二次函数,且f(0)=1,f(x+1) 一
f(x)=2x, 求f(x)
知识点二求函数的解析式
(翻折法)先画出函数y=x的图像
然后把图像中位于横轴下方的部分翻转到上方即可.
知识点三 画函数图像
【例5】画出函数y=|x| 的图像
【解】由绝对值的概念,
例题讲解
画出图像如图:
分段函数
在定义域内自变量x的不同的取值范围上,有 不同的对应关系的函数叫分段函数.
注:(1)分段函数是一个函数,不要把它误认为是几个 函数;
(2)分段函数的定义域是各段定义域的并集, 值域是各段值域的并集.
知识点三 画函数图像
所以函数的图像如图所示:
【解法二】(翻折法)先画出函数y=x-2的图像
然后把图像中位于横轴下方的部分翻转到上方即可.
变式1:画出函数y=lx-2I的图像.
【解法一】由绝对值的概念可知,
知识点三 画函数图像
知识点三 画函数图像
变式2:画函数y=lx -11的图像.
例6、给定函数f(x)=x+1,g(x)=(x+1) ,x∈R
(1)在同一个坐标系中画出函数f(x),g(x)的图像;
(2)Vx∈R,用M (x)表示f(x),g(x)中的较大者,记为M (x)=max{f(x),g(x)}. 例如当x=2,M(x)=max{f(2),g(2)}=max{3,9}=9, 请分别用图象法与解析
知识点三 画函数图像
法表示函数M(x)
由 (x+1) =x+1, 得x(x+1)=0
解 得:x=-1 或x=0
结合图象,得出函数的解析式为
因为2>0
所以M(2)=(2+1) =9
因为-a -1<-1
所以M(-a -1)=(-a -1+1) =a (4)求函数的值域
值域为(-1,+0)
( 5 ) 解M(x)>1 的解集
令 (x +1)=1
得x=0,x=-2
4
3
2
l
-5 -4 -3 -2 -1
-1
-2
所以不等式的解集为(-0,- 1)U(2,+
(3)求M(2),M(-a -1)
1 2 3 4
X
o
(1)试求f(-5),f (一 √3), 的值.(2)本例条件不变,若f(a)=3, 求实数a 的值.
1已知函数
(2)注意分段函数的表示方法及其图象的画法.
(3)函数解析式的求法.
2.本节课运用了什么数学思想方法
数形结合
解析式法
图象法
列表法
小 结
1.本节课学习了什么知识点
(1) 函数的表示法
新高考新教材
高中数第一册第三章函数的概念与性质
3.1.2
函数的表示法
x 叫做自变量,x 的取值范围构成的集合A叫
做函数的定义域;与x的值相对应的y值叫做函数值, 所有函数值组成的集合叫做函数的值域。
函数值的集合{f(x)lx∈A}
函数的三要素:定义域、值域、对应关系
知识回顾 设A、B是非空数集,如果对于集合A中的任意
一个数x, 按照某种确定的对应关系f, 在集合B 中都有唯一确定的数y和它对应,就称
f:A→B 为从集合A到集合B的一个函数,
记作: y=f(x),x∈A
我们初中已经接触函数几种常用的表示法
1、解析法:用数学表达式表示两个变量之间的对应关系;
2、图象法:用图象表示两个变量之间的对应关系;
3、列表法:用表格表示两个变量之间的对应关系.
正比例函数 y=kx(k≠0)
一次函数 y=kx+b(k≠0)
k>0,b>0
解 析 法用数学表达式表示两个变量之间的对应关系。
图 象法 用图象表示两个变量之间的对应关系.
a>0
知识点一函数的表示法
二次函数y=ax +bx+c(a≠0)
反比例函数
冽题讲解
【例4】某种笔记本的单价是5元,买m(m∈{1,2,3,4,5})个笔记本需要y
元.试用函数的三种表示法来表示函数y= f(m).
【图像法】函数图像可以表示如图:
【解析法】y=5m,m∈{1,2,3,4,5}
笔记本数m 1 2 3 4
5
钱数y 5 10 15 20
25
【列表法】函数可以表示如下表:
优点 缺点
联系
解 析 法 ①简明、全面地概括了变 量间的关系;②可以通过 解析式求出任意一个自变 量的值所对应的函数值; ③便于研究函数性质. 不够形象、直观、 具体,并不是所有 的函数都能用解析 法表示出来.
三种方 法之间有 时可以相 互转化, 面对实际 情景时, 我们要根 据不同的 需要选择 恰当的表 示法表示 函数 .
图 像 法 直观形象地表示出函数 的变化情况,有利于通过 图象研究函数的某些性质. 只能近似地求出 自变量的值所对应 的函数值,而且有 时误差太大.
列 表 法 不通过计算就可以直 接看出与自变量对应的 函数值. 只能表示自变量 取值较少的有限的 对应关系.
思考2
比较函数的三种表示法,它们各自的特点是什么
解:由题意得,设f(x)=ax+b(a≠0) 因为3f(x+1)-f(x)=2x+9
所以3a(x+1)+3b-ax-b=2x+9 由等式的性质得
例1已知f(x) 一次函数,且满足3f(x+1)-f(x)=2x+9, 求函数
f(x) 解析式。
解得a=1,b=3
所以所求函数解析式为f(x)=x+3
知识点二求函数的解析式
待定系数法
知识点二求函数的解析式
例 2 若f(2x+1)=6x+5, 求函数f(x) 解析式
设2x+1=t,
所以f(t)=6
所以f(x)=3x+2
换元法
国
知识点二求函数的解析式
例 3 若f(x)+2f(-x)=x +2x,
f(x)+2f(-x)=x2+2x
令x=-x得
f(-x)+2f
联立两式
得
求函数f(x) 解析式
方程的思想
1求下列函数的解析式:
(1)已知函数f(x+1)=x+2 √x, 求f(x);
(2)已知函数f(x)是二次函数,且f(0)=1,f(x+1) 一
f(x)=2x, 求f(x)
知识点二求函数的解析式
(翻折法)先画出函数y=x的图像
然后把图像中位于横轴下方的部分翻转到上方即可.
知识点三 画函数图像
【例5】画出函数y=|x| 的图像
【解】由绝对值的概念,
例题讲解
画出图像如图:
分段函数
在定义域内自变量x的不同的取值范围上,有 不同的对应关系的函数叫分段函数.
注:(1)分段函数是一个函数,不要把它误认为是几个 函数;
(2)分段函数的定义域是各段定义域的并集, 值域是各段值域的并集.
知识点三 画函数图像
所以函数的图像如图所示:
【解法二】(翻折法)先画出函数y=x-2的图像
然后把图像中位于横轴下方的部分翻转到上方即可.
变式1:画出函数y=lx-2I的图像.
【解法一】由绝对值的概念可知,
知识点三 画函数图像
知识点三 画函数图像
变式2:画函数y=lx -11的图像.
例6、给定函数f(x)=x+1,g(x)=(x+1) ,x∈R
(1)在同一个坐标系中画出函数f(x),g(x)的图像;
(2)Vx∈R,用M (x)表示f(x),g(x)中的较大者,记为M (x)=max{f(x),g(x)}. 例如当x=2,M(x)=max{f(2),g(2)}=max{3,9}=9, 请分别用图象法与解析
知识点三 画函数图像
法表示函数M(x)
由 (x+1) =x+1, 得x(x+1)=0
解 得:x=-1 或x=0
结合图象,得出函数的解析式为
因为2>0
所以M(2)=(2+1) =9
因为-a -1<-1
所以M(-a -1)=(-a -1+1) =a (4)求函数的值域
值域为(-1,+0)
( 5 ) 解M(x)>1 的解集
令 (x +1)=1
得x=0,x=-2
4
3
2
l
-5 -4 -3 -2 -1
-1
-2
所以不等式的解集为(-0,- 1)U(2,+
(3)求M(2),M(-a -1)
1 2 3 4
X
o
(1)试求f(-5),f (一 √3), 的值.(2)本例条件不变,若f(a)=3, 求实数a 的值.
1已知函数
(2)注意分段函数的表示方法及其图象的画法.
(3)函数解析式的求法.
2.本节课运用了什么数学思想方法
数形结合
解析式法
图象法
列表法
小 结
1.本节课学习了什么知识点
(1) 函数的表示法
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
