4-4-2对数函数的图象和性质(一)课件-人教A版(2019)高中数学必修第一册
文档属性
| 名称 | 4-4-2对数函数的图象和性质(一)课件-人教A版(2019)高中数学必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-05 18:12:15 | ||
图片预览









文档简介
(共56张PPT)
学习目标 -------
1 . 初步掌握对数函数的图象和性质 .2 . 会类比指数函数研究对数函数的性质 .3 . 掌握对
数函数的图象和性质的简单应用 .
4.4 对 数 函 数
4.4.2 对数函数的图象和性质(一)
随堂检测内化素养
自主阅读新知预习
课时作业分层自检
合作探究深化提能
自主阅读·新知预习
随堂检测内化素养
合作探究深化提能
自主阅读新知预习
课时作业分层自检
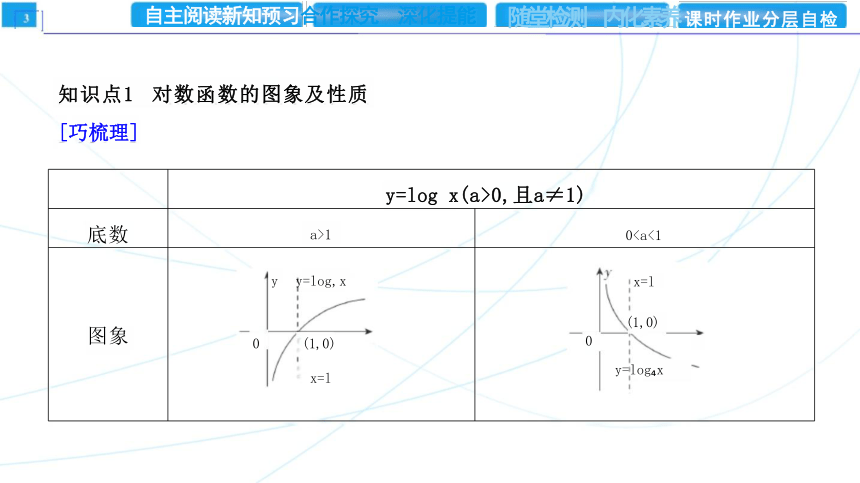
y=log x(a>0,且a≠1)
底数 a>1
0图象 y y=log,x 0 (1,0) x=l
x=l
(1,0)
0
y=log x
知识点1 对数函数的图象及性质
[巧梳理]
随堂检测 内化素养 课时作业分层自检
自主阅读新知预习合作探究 深化提能
y=log x(a>0,且a≠1)
定义域
(0,十
值域
R
单调性
在(0,十一)上是增函数 在(0,十一)上是减函数
最值
无最大、最小值
奇偶性
非奇非偶函数
共点性
图象过定点_ (1,0) , 即x=1 时 ,y=0
随堂检测内化素养
合作探究 深化提能
课时作业分层自检
自主阅读新知预习
y=logax(a>0,且a≠1)
函数 值特点 x∈(0,1)时, 0) x∈(1,十一)时,
x∈(0,1)时,
y∈ (0,十一)
x∈[1,十一]时,
y -0 ,0]
对称性 函数y=logx与y=l g图x象关于__x 轴 对称
自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
[微点拨]
(1)函数图象只出现在y轴右侧;(2)当01
时,底数越大,图象越靠近x 轴;(4)任意底数互为倒数的两个对数函数的图象关于x 轴 对
称 .
自主阅读新知预习 合作探究深化提能 随堂检测内化素养 课时作业分层自检
A B C D
解析:C y=1g x向左平移1个单位得y=1g(x+1).
[微体验]
1. 函数y=lg(x+1) 的图象大致是( C )
自主阅读新知预习合作探究深化提能 随堂检测内化素养课时作业分层自检
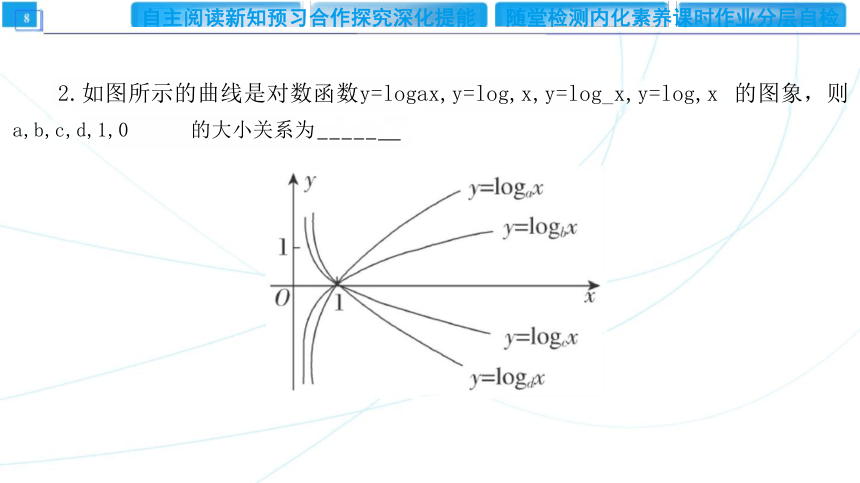
2.如图所示的曲线是对数函数y=logax,y=log,x,y=log_x,y=log,x 的图象,则
a,b,c,d,1,0 的大小关系为
自主阅读新知预习合作探究深化提能
随堂检测内化素养课时作业分层自检
解 析 :由题图可知函数y=log x,y=log,x 的底数a>1,b>1, 函 数y=logx,y=log,x
的底数0横坐标从左向右依次为c,d,a,b, 显 然b>a>1>d>c>0.
答案: b>a>1>d>c>0
自主阅读新知预习合作探究深化提能 随堂检测内化素养课时作业分层自检
知识点2 反函数
[巧梳理]
一般地,指数函数y=a*(a>0, 且a≠1) 与对数函数y=logax(a>0, 且a≠1) 互为反函 数.它们的_ 定义域 和 值域 正好互换.图象关于直线__y=x 对
称 .
随堂检测 内化素养 1 课时作业分层自检
合作探究深化提能
自主阅读新知预习
10
[微体验]
3 . 若函数y=f(x) 是函数y=3× 的反函数,则
解析:fx)=logx,
答案: - log 2
自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
的值为
■
合作探究·深化提能
随堂检测内化素养
合作探究深化提能
自主阅读新知预习
课时作业分层自检
学习任务一 对数函数的图象
[例1] (1)如图,若C ,C 分别为函数y=logax 和y=log,x 的图象,则( )
A.0B.0C.a>b>1
D.b>a>1
(2)若函数y=loga(x+b)+c(a>0, 且 a≠1) 的图象恒过定点(3,2),则实数b=
,C=__ __.
(3)已知f(x)=logax(a>0,且a≠1)满足f(-5)=1, 试画出函数f(x)的图象.
自主阅读新知预习合作探究深化提能
随堂检测内化素养课时作业分层自检
13
解析: (1)作直线y=1, 则直线与C ,C 的交点的横坐标分别为a,b, 易知0(2)∵函数的图象恒过定点(3,2),
∴将(3,2)代入y=loga(x+b)+c,
得 2 =loga(3+b)+c.
又当a>0, 且a≠1 时 ,loga1=0 恒成立,
∴c=2,3+b=1,∴b=-2,c=2.
14 自主阅读新知预习合作探究深化提能 随堂检测内化素养课时作业分层自检
15 自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
(3)因为f(一5)=1,所以loga5=1, 即 a=5,
所以函数f(x)=log |x|的图象如图所示.
y
1
0
-5 1
答 案 :(1)B (2)-22
5 X
2
16 自主阅读新知预习合作探究深化提能 随堂检测内化素养课时作业分层自检
[发散思维]
1.( 变问法) 在本例(3)中,若条件不变,试画出函数g(x)=logax-1| 的图象.
解 :因 为f(x)=log x|, 所 以g(x)=log x-1|,
如 图 ,g(x) 的图象是由f(x)的图象向右平移1个单位长度得到的.
自主阅读新知预习合作探究深化提能 随堂检测内化素养课时作业分层自检
2. (变问法) 在本例(3)中,若条件不变,试画出函数h(x)=|logax|的图象.
解 :因 为a=5, 所以h(x)=|log x|.h(x) 的图象如图所示.
■方法技巧
对数型函数图象的变换方法
(1)作y=f(x|)的图象时,保留y=f(x)(x≥0)图象不变,x<0 时 ,y=f(lx|)的图象与y=
f(x)(x>0)的图象关于y轴对称.
(2)作y=|f(x)|的图象时,保留y=f(x)的x轴及上方图象不变,把x轴下方图象以x轴为对
称轴翻折上去即可.
(3)有关对数函数平移也符合“左加右减,上加下减”的规律.
(4)y=f(=x) 与y=f(x) 关于y轴对称,y=-f(x) 与y=f(x) 关于x轴对称,y=-f(-x) 与y
=f(x)关于原点对称 .
合作探究深化提能
自主阅读新知预习
随堂检测内化素养
课时作业分层自检
18
学习任务二 利用单调性比较对数值的大小
[例2] ( 链接教材P 33例3)比较下列各组中两个值的大小;
(1)log 1.9,log 2;
(2)log 3,log .32;
(3)log π,loga3.14(a>0, 且a≠1);
(4)log 0.4,log 0.4.
解 :(1)因为y=log x 在(0,+一)上单调递增,1.9<2,
所以log 1.9(2)因为log 3>log 1=0,logo.32所以log 3>logo.32.
19 自主阅读新知预习合作探究深化提能 随堂检测内化素养课时作业分层自检
(3)当a>1 时,函数y=log x 在(0,+一)上单调递增,则有logπ>loga3.14;
当0综上所述,当a>1 时 ,logaπ>loga3.14;
当0(4)在同一直角坐标系中,作出y=log X,y=log x 的图象,再作出直线x=0.4 (图略),
观察图象可得log 0.420 自主阅读新知预习合作探究深化提能 随堂检测内化素养课时作业分层自检
方法技巧
比较对数值大小时常用的四种方法
(1)同底数的利用对数函数的单调性.
(2)同真数的利用对数函数的图象或用换底公式转化.
(3)底数和真数都不同,找中间量.
(4)若底数为同一参数,则根据底数对对数函数单调性的影响,对底数进行分类讨
论 .
21 自主阅读新知预习 合作探究深化提能 随堂检测内化素养 课时作业分层自检
22 自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
[跟踪训练]
1. 比较大小:
(1)loga5.1,loga5.9(a>0, 且 a≠1);
(2)log π,log √3,log √2.
解 :(1)当a>1 时 ,y=logx 在(0,+一)上是增函数,
又5.1<5.9,所以loga5.1当0又5.1<5.9,所以loga5.1>loga5.9.
综上,当a>1 时 ,loga5.1当0log 5.9.
又 ,log π>1,
∴log π>log √3>log \2.
23 自主阅读新知预习合作探究 深化提 随堂检测内化素养课时作业分层自检
:
又 124 自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
学习任务三 解对数不等式
[例3] 解下列不等式:
② ;
(3)loga(2x—5)>loga(x—1).
解 :(1)由题意可得
解得0所以原不等式的解集为(0,2).
25 自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
(2)当x>1 时 ,
解得 此时不等式无解.
当 0解得 所
综上所述,原不等式的解集
26 自主阅读新知预习合作探究深化提能 随堂检测内化素养课时作业分层自检
(3)当a>1 时,原不等式等价于
解得x>4.
当 0解
综上所述,当 a>1 时,原不等式的解集为{x|x>4}. 当 0■方法技巧■-
两类对数不等式的解法
(1)形如log f(x)①当0g(x)>0;
②当a>1时,可转化为0(2)形如log f(x)①当0ab;
②当a>1时,可转化为0[提醒] 解决与对数函数相关的问题时要遵循定义域优先原则.
随堂检测内化素养 课时作业分层自检
合作探究深化提能
自主阅读新知预习
27
28 自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
[跟踪训练]
2 . 已知logo.22x解 析 :因 为 函 数 y=logo.2x 在(0,十一)上是减函数,所以由 logo.22x解 得x>1, 即 x 的取值范围为(1,十一).
答案:(1,十一)
3 . 已知函数f(x)=loga(x+3) 在区间[-2,- 1]上总有 |f(x)|<2, 求实数a 的取值范围.
解:因 为x∈[-2,—1], 所以1≤x+3≤2.
当 a>1 时 ,loga1≤loga(x+3)≤loga2, 即 O≤f(x)≤loga2.
因为对任意的x∈[-2,—1],|f(x)<2 恒成立,
所 解得a
o
29 自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
2
30 自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
当0即 loga2≤f(x)≤0.
因为对任意的x∈[-2,—1],|f(x)<2 恒成立,
所 解 得
综上可得,实数a 的取值范围是(0, √2
2
随堂检测·内化素养
随堂检测内化素养
合作探究深化提能
自主阅读新知预习
课时作业分层自检
A B C D
解 析 :A ∵0又函数y=loga(x-1) 的图象是由y=log x的图象向右平移1个单位长度得到的,故A 正
确 .
自主阅读新知预习合作探究深化提能 随堂检测 内化素养课时作业分层自检A
1 . 函 数y=loga(x-1)(032
2 . 若a=20.2,b=log 3.2,c=log 0.5, 则( A )
A.a>b>c B.b>a>c
C.c>a>b D.b>c>a
解 析 :A ∵a=20.2>1>b=log 3.2>0>c=-1,
∴a>b>c.
33 自主阅读新知预习合作探究深化提能 随堂检测内化素养课时作业分层自检
34 自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
3.不等式
A. ( 一 0 , 3 )
的解集为( D )
B.
由题意可
解析:D
解
D.
35 自主阅读新知预习合作探究 深化提能1 随堂检测内化素养课时作业分层自检
4 . 若 且a≠1), 则 a 的取值范围为 .
解析: 当 a>1 时 , 满足条件;
当 0,∴ 重
综上可知,a 的取值范围为(0,
答案:(0,
: ·
课时作业·分层自检
随堂检测内化素养
合作探究深化提能
自主阅读新知预习
课时作业分层自检
基础巩固练
1 .若1g(2x-4)≤1, 则x的取值范围是( B )
A. ( 一 0 , 7 ) B.[2,7]
C.(7, 十 一 ) D.(2, 十一)
解析: B 由1g(2x-4)≤1, 得0<2x-4≤10, 即 237 自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
l 23 4 5 6 7 8 9 10 11 12 13 14
2 . 设a=log 7,b=21.1,c=0.831, 则( B )
A.bC.c解析:B ∵a=log 7,∴1∵b=21.1,∴b>2.
∵c=0.83.1,∴038 自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
1 2 3 4 5 6 7 8 9 10 11 12 13 14
3 . 函数f(x)=log x(OA.0 B.1
C.2 D.a
解析: C ∵0∴f(x)=log x在[a ,a] 上单调递减,
∴f(x)max=f(a )=logaa =2.
39 自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
1 2 3 4 5 6 7 8 9 10 11 12 13 14
4 . 若y=loga(3a-1) 恒为正值,则a 的取值范围为( D )
A.
B.
C.(1, 十 一 )
D.
40 自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
1 234 5 6 7 8 9 10 11 12 13 14
解 析 :D 因 为y=loga(3a-1) 恒为正值,
所
解 或a>1. 故选D.
自主阅读新知预习合作探究深化提能 随堂检测内化素养课时作业分层自检
1 234 5 7 8 9 10 11 12 13 14
41
解 析 :B 由f(x) 的定义域为( - 一 , - 1)U(1,+), 且f(-x)=1g(|-x|-1)=1g()x|-
1)=f(x), 得 f(x)是偶函数,由此知C,D 错误;又当x>1 时 ,f(x)=1g(x-1) 在(1,+ 一 )上单
调递增,所以B正确 .
随堂检测内化素养课时作业分层自检
自主阅读新知预习合作探究深化提能
5. 函 数f(x)=1g()x|-1) 的大致图象是( B )
1 2 3 4 5 6 7 8 9 10 11 12 13 14
42
A
D
C
B
A B C D
解析:AB
∴f(x)和g(x)的单调性相同,
结合选项可知A,B 正确。
1 2 3 4 8 9 10 11 12 13 14
6.(多选)已知a>0,b>0, 且ab=1,a≠1, 则函数f(x)=a 与函数g(x)=—log,x 在同
一坐标系中的图象可能是(AB )
自主阅读新知预习合作探究深化提能
随堂检测内化素养课时作业分层自检
y
l
0
43
X
综 上 , 实 数a 的取值范围是(1,2) .
答案:(1,2)
1 23 4 5 6 7 8 9 10 11 12 13 14
7 . 如果函数f(x)=(3-a) 与g(x)=logax(a>0, 且a≠1) 的增减性相同,则实数a 的取值
范围是 .
解 析 :若 f(x),g(x) 均为增函数,则
即 1若f(x),g(x) 均为减函数,则
44 自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
无解 .
8 . 已知函数f(x)=log x(01, 则f(x)<0;② 若O则f(x)>0;③ 若f(x )>f(x ),则x >x ;④f(xy)=f(x)+f(y).
其中正确的命题的序号有__ .
解 析 :若 x>1, 则f(x)<0; 若 O0; 若f(x )>f(x ), 则x 满足xy>0, 但f(x),f(y) 无意义,故f(xy)=f(x)+f(v) 不一定成立.故①②正确.
答案: ①②
45 自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
1 2 3 4 5 6 7 8 9 10 11 12 13 14
解 :先作出函数y=1gx 的图象,再将图象位于x 轴下方的部分
以x 轴为对称轴翻折到x 轴上方,于是得f(x)=|lg x|图象(如图),由
图象可知,f(x) 在(0,1)上单调递减,在(1,十一)上单调递增.
由 得
又
46 自主阅读新知预习合作探究深化提能 随堂检测内化素养课时作业分层自检
9. 已知f(x)=|lg x|, 试借助图象比较f(a),f(b),f(c)的大小.
f(x)=1lg x
X
1 2 3 4 5 6 7 10 11 12 13 14
Y
0
1
综合应用练
10.若函数f(x)=loga(x+b)的图象如图所示,其中a,b 为常数,则函数g(x)=a+b 的
图象大致是( D )
自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
A
7 8 9 10 11 12 13 14
D
C
B
解 析 :D 由 f(x)的图象可知O1,
∴g(x) 的图象应为D.
随 堂 检 测 内化素养 1 课时作业分层自检
合作探究深化提能
1 23 4 5 6 7 8 9 10 11 12 13 14
自主阅读新知预习
48
11.设偶函数f(x)=logax-b| 在(一一,0)上单调递增,则f(a+1) 与f(b+2) 的大小关系
是( D )
A.f(a+1)B.f(a+1)≤f(b+2)
C.f(a+1)≥f(b+2)
D.f(a+1)>f(b+2)
49 自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
1 2 3 4 5 6 7 8 9 10 ll 12 13 14
解析: D 因为函数f(x)是偶函数,所以b=0,
又函数在(-0,0)上单调递增,所以函数在(0,+一)上单调递减,则01因为f(a+1)=loga|a+1|,f(b+2)=loga2,
且1所以f(a+1)>f(b+2).
50 自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
1 23 4 5 6 7 8 9 10 ll 12 13 14
51 自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
12 . 已知f(x) 是定义在R 上的偶函数,且在[0,十一]上单调递增, 则不等式
的解集为 .
解 析 :∵f(x) 是 R 上的偶函数,
∴它的图象关于y 轴对称 .
∵f(x)在[0,十]上单调递增,
∴f(x)在[一一,0]上单调递减,
由 得 则函数的大致图象如图所示.
1 2 3 4 5 6 7 8 9 10 11 12 13 14
或
解得x>2 或
52 自主阅读新知预习合作探究深化提能 随堂检测内化素养课时作业分层自检
1 2 3 4 8 10 1112 13 14
∴原不
答案:
: ·
6 5 工
y
X
0
1
53 自主阅读新知预习合作探究深化提能0 随堂检测内化素养课时作业分层自检
13.已知 的值域为R, 那么实数a 的取值范围是_
解 析 :要使函数f(x)的值域为R,
则必须满
所以
答案:
12 13 14
14.若不等式x —logx<0 内恒成立,求实数m 的取值范围.
解 :由 x -log,x<0, 得 x的草图,如图所示.
要使x=x 图象的上方,于是054 自主阅读新知预习合作探究深化提能 随堂检测内化素养课时作业分层自检
探索创新练
1 2 3 4 5 6 7 8 10 11 12 1314
yA
1
0
1
2
X
55 自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
即实数m 的取值范围
∵当 时,
∴只要当
即 .又01 2 3 4 5 6 7 10 11 12 1314
即可,
本部分内容讲解结束
合作探究深化提能
随堂检测内化素养
自主阅读新知预习
课时作业分层自检
学习目标 -------
1 . 初步掌握对数函数的图象和性质 .2 . 会类比指数函数研究对数函数的性质 .3 . 掌握对
数函数的图象和性质的简单应用 .
4.4 对 数 函 数
4.4.2 对数函数的图象和性质(一)
随堂检测内化素养
自主阅读新知预习
课时作业分层自检
合作探究深化提能
自主阅读·新知预习
随堂检测内化素养
合作探究深化提能
自主阅读新知预习
课时作业分层自检
y=log x(a>0,且a≠1)
底数 a>1
0
x=l
(1,0)
0
y=log x
知识点1 对数函数的图象及性质
[巧梳理]
随堂检测 内化素养 课时作业分层自检
自主阅读新知预习合作探究 深化提能
y=log x(a>0,且a≠1)
定义域
(0,十
值域
R
单调性
在(0,十一)上是增函数 在(0,十一)上是减函数
最值
无最大、最小值
奇偶性
非奇非偶函数
共点性
图象过定点_ (1,0) , 即x=1 时 ,y=0
随堂检测内化素养
合作探究 深化提能
课时作业分层自检
自主阅读新知预习
y=logax(a>0,且a≠1)
函数 值特点 x∈(0,1)时, 0) x∈(1,十一)时,
x∈(0,1)时,
y∈ (0,十一)
x∈[1,十一]时,
y -0 ,0]
对称性 函数y=logx与y=l g图x象关于__x 轴 对称
自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
[微点拨]
(1)函数图象只出现在y轴右侧;(2)当0
时,底数越大,图象越靠近x 轴;(4)任意底数互为倒数的两个对数函数的图象关于x 轴 对
称 .
自主阅读新知预习 合作探究深化提能 随堂检测内化素养 课时作业分层自检
A B C D
解析:C y=1g x向左平移1个单位得y=1g(x+1).
[微体验]
1. 函数y=lg(x+1) 的图象大致是( C )
自主阅读新知预习合作探究深化提能 随堂检测内化素养课时作业分层自检
2.如图所示的曲线是对数函数y=logax,y=log,x,y=log_x,y=log,x 的图象,则
a,b,c,d,1,0 的大小关系为
自主阅读新知预习合作探究深化提能
随堂检测内化素养课时作业分层自检
解 析 :由题图可知函数y=log x,y=log,x 的底数a>1,b>1, 函 数y=logx,y=log,x
的底数0
答案: b>a>1>d>c>0
自主阅读新知预习合作探究深化提能 随堂检测内化素养课时作业分层自检
知识点2 反函数
[巧梳理]
一般地,指数函数y=a*(a>0, 且a≠1) 与对数函数y=logax(a>0, 且a≠1) 互为反函 数.它们的_ 定义域 和 值域 正好互换.图象关于直线__y=x 对
称 .
随堂检测 内化素养 1 课时作业分层自检
合作探究深化提能
自主阅读新知预习
10
[微体验]
3 . 若函数y=f(x) 是函数y=3× 的反函数,则
解析:fx)=logx,
答案: - log 2
自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
的值为
■
合作探究·深化提能
随堂检测内化素养
合作探究深化提能
自主阅读新知预习
课时作业分层自检
学习任务一 对数函数的图象
[例1] (1)如图,若C ,C 分别为函数y=logax 和y=log,x 的图象,则( )
A.0
D.b>a>1
(2)若函数y=loga(x+b)+c(a>0, 且 a≠1) 的图象恒过定点(3,2),则实数b=
,C=__ __.
(3)已知f(x)=logax(a>0,且a≠1)满足f(-5)=1, 试画出函数f(x)的图象.
自主阅读新知预习合作探究深化提能
随堂检测内化素养课时作业分层自检
13
解析: (1)作直线y=1, 则直线与C ,C 的交点的横坐标分别为a,b, 易知0
∴将(3,2)代入y=loga(x+b)+c,
得 2 =loga(3+b)+c.
又当a>0, 且a≠1 时 ,loga1=0 恒成立,
∴c=2,3+b=1,∴b=-2,c=2.
14 自主阅读新知预习合作探究深化提能 随堂检测内化素养课时作业分层自检
15 自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
(3)因为f(一5)=1,所以loga5=1, 即 a=5,
所以函数f(x)=log |x|的图象如图所示.
y
1
0
-5 1
答 案 :(1)B (2)-22
5 X
2
16 自主阅读新知预习合作探究深化提能 随堂检测内化素养课时作业分层自检
[发散思维]
1.( 变问法) 在本例(3)中,若条件不变,试画出函数g(x)=logax-1| 的图象.
解 :因 为f(x)=log x|, 所 以g(x)=log x-1|,
如 图 ,g(x) 的图象是由f(x)的图象向右平移1个单位长度得到的.
自主阅读新知预习合作探究深化提能 随堂检测内化素养课时作业分层自检
2. (变问法) 在本例(3)中,若条件不变,试画出函数h(x)=|logax|的图象.
解 :因 为a=5, 所以h(x)=|log x|.h(x) 的图象如图所示.
■方法技巧
对数型函数图象的变换方法
(1)作y=f(x|)的图象时,保留y=f(x)(x≥0)图象不变,x<0 时 ,y=f(lx|)的图象与y=
f(x)(x>0)的图象关于y轴对称.
(2)作y=|f(x)|的图象时,保留y=f(x)的x轴及上方图象不变,把x轴下方图象以x轴为对
称轴翻折上去即可.
(3)有关对数函数平移也符合“左加右减,上加下减”的规律.
(4)y=f(=x) 与y=f(x) 关于y轴对称,y=-f(x) 与y=f(x) 关于x轴对称,y=-f(-x) 与y
=f(x)关于原点对称 .
合作探究深化提能
自主阅读新知预习
随堂检测内化素养
课时作业分层自检
18
学习任务二 利用单调性比较对数值的大小
[例2] ( 链接教材P 33例3)比较下列各组中两个值的大小;
(1)log 1.9,log 2;
(2)log 3,log .32;
(3)log π,loga3.14(a>0, 且a≠1);
(4)log 0.4,log 0.4.
解 :(1)因为y=log x 在(0,+一)上单调递增,1.9<2,
所以log 1.9
19 自主阅读新知预习合作探究深化提能 随堂检测内化素养课时作业分层自检
(3)当a>1 时,函数y=log x 在(0,+一)上单调递增,则有logπ>loga3.14;
当0
当0
观察图象可得log 0.4
方法技巧
比较对数值大小时常用的四种方法
(1)同底数的利用对数函数的单调性.
(2)同真数的利用对数函数的图象或用换底公式转化.
(3)底数和真数都不同,找中间量.
(4)若底数为同一参数,则根据底数对对数函数单调性的影响,对底数进行分类讨
论 .
21 自主阅读新知预习 合作探究深化提能 随堂检测内化素养 课时作业分层自检
22 自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
[跟踪训练]
1. 比较大小:
(1)loga5.1,loga5.9(a>0, 且 a≠1);
(2)log π,log √3,log √2.
解 :(1)当a>1 时 ,y=logx 在(0,+一)上是增函数,
又5.1<5.9,所以loga5.1
综上,当a>1 时 ,loga5.1
又 ,log π>1,
∴log π>log √3>log \2.
23 自主阅读新知预习合作探究 深化提 随堂检测内化素养课时作业分层自检
:
又 1
学习任务三 解对数不等式
[例3] 解下列不等式:
② ;
(3)loga(2x—5)>loga(x—1).
解 :(1)由题意可得
解得0
25 自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
(2)当x>1 时 ,
解得 此时不等式无解.
当 0
综上所述,原不等式的解集
26 自主阅读新知预习合作探究深化提能 随堂检测内化素养课时作业分层自检
(3)当a>1 时,原不等式等价于
解得x>4.
当 0
综上所述,当 a>1 时,原不等式的解集为{x|x>4}. 当 0
两类对数不等式的解法
(1)形如log f(x)
②当a>1时,可转化为0
②当a>1时,可转化为0
随堂检测内化素养 课时作业分层自检
合作探究深化提能
自主阅读新知预习
27
28 自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
[跟踪训练]
2 . 已知logo.22x
答案:(1,十一)
3 . 已知函数f(x)=loga(x+3) 在区间[-2,- 1]上总有 |f(x)|<2, 求实数a 的取值范围.
解:因 为x∈[-2,—1], 所以1≤x+3≤2.
当 a>1 时 ,loga1≤loga(x+3)≤loga2, 即 O≤f(x)≤loga2.
因为对任意的x∈[-2,—1],|f(x)<2 恒成立,
所 解得a
o
29 自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
2
30 自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
当0
因为对任意的x∈[-2,—1],|f(x)<2 恒成立,
所 解 得
综上可得,实数a 的取值范围是(0, √2
2
随堂检测·内化素养
随堂检测内化素养
合作探究深化提能
自主阅读新知预习
课时作业分层自检
A B C D
解 析 :A ∵0
确 .
自主阅读新知预习合作探究深化提能 随堂检测 内化素养课时作业分层自检A
1 . 函 数y=loga(x-1)(0
2 . 若a=20.2,b=log 3.2,c=log 0.5, 则( A )
A.a>b>c B.b>a>c
C.c>a>b D.b>c>a
解 析 :A ∵a=20.2>1>b=log 3.2>0>c=-1,
∴a>b>c.
33 自主阅读新知预习合作探究深化提能 随堂检测内化素养课时作业分层自检
34 自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
3.不等式
A. ( 一 0 , 3 )
的解集为( D )
B.
由题意可
解析:D
解
D.
35 自主阅读新知预习合作探究 深化提能1 随堂检测内化素养课时作业分层自检
4 . 若 且a≠1), 则 a 的取值范围为 .
解析: 当 a>1 时 , 满足条件;
当 0
综上可知,a 的取值范围为(0,
答案:(0,
: ·
课时作业·分层自检
随堂检测内化素养
合作探究深化提能
自主阅读新知预习
课时作业分层自检
基础巩固练
1 .若1g(2x-4)≤1, 则x的取值范围是( B )
A. ( 一 0 , 7 ) B.[2,7]
C.(7, 十 一 ) D.(2, 十一)
解析: B 由1g(2x-4)≤1, 得0<2x-4≤10, 即 2
l 23 4 5 6 7 8 9 10 11 12 13 14
2 . 设a=log 7,b=21.1,c=0.831, 则( B )
A.b
∵c=0.83.1,∴0
1 2 3 4 5 6 7 8 9 10 11 12 13 14
3 . 函数f(x)=log x(O
C.2 D.a
解析: C ∵0
∴f(x)max=f(a )=logaa =2.
39 自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
1 2 3 4 5 6 7 8 9 10 11 12 13 14
4 . 若y=loga(3a-1) 恒为正值,则a 的取值范围为( D )
A.
B.
C.(1, 十 一 )
D.
40 自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
1 234 5 6 7 8 9 10 11 12 13 14
解 析 :D 因 为y=loga(3a-1) 恒为正值,
所
解 或a>1. 故选D.
自主阅读新知预习合作探究深化提能 随堂检测内化素养课时作业分层自检
1 234 5 7 8 9 10 11 12 13 14
41
解 析 :B 由f(x) 的定义域为( - 一 , - 1)U(1,+), 且f(-x)=1g(|-x|-1)=1g()x|-
1)=f(x), 得 f(x)是偶函数,由此知C,D 错误;又当x>1 时 ,f(x)=1g(x-1) 在(1,+ 一 )上单
调递增,所以B正确 .
随堂检测内化素养课时作业分层自检
自主阅读新知预习合作探究深化提能
5. 函 数f(x)=1g()x|-1) 的大致图象是( B )
1 2 3 4 5 6 7 8 9 10 11 12 13 14
42
A
D
C
B
A B C D
解析:AB
∴f(x)和g(x)的单调性相同,
结合选项可知A,B 正确。
1 2 3 4 8 9 10 11 12 13 14
6.(多选)已知a>0,b>0, 且ab=1,a≠1, 则函数f(x)=a 与函数g(x)=—log,x 在同
一坐标系中的图象可能是(AB )
自主阅读新知预习合作探究深化提能
随堂检测内化素养课时作业分层自检
y
l
0
43
X
综 上 , 实 数a 的取值范围是(1,2) .
答案:(1,2)
1 23 4 5 6 7 8 9 10 11 12 13 14
7 . 如果函数f(x)=(3-a) 与g(x)=logax(a>0, 且a≠1) 的增减性相同,则实数a 的取值
范围是 .
解 析 :若 f(x),g(x) 均为增函数,则
即 1
44 自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
无解 .
8 . 已知函数f(x)=log x(0
其中正确的命题的序号有__ .
解 析 :若 x>1, 则f(x)<0; 若 O
答案: ①②
45 自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
1 2 3 4 5 6 7 8 9 10 11 12 13 14
解 :先作出函数y=1gx 的图象,再将图象位于x 轴下方的部分
以x 轴为对称轴翻折到x 轴上方,于是得f(x)=|lg x|图象(如图),由
图象可知,f(x) 在(0,1)上单调递减,在(1,十一)上单调递增.
由 得
又
46 自主阅读新知预习合作探究深化提能 随堂检测内化素养课时作业分层自检
9. 已知f(x)=|lg x|, 试借助图象比较f(a),f(b),f(c)的大小.
f(x)=1lg x
X
1 2 3 4 5 6 7 10 11 12 13 14
Y
0
1
综合应用练
10.若函数f(x)=loga(x+b)的图象如图所示,其中a,b 为常数,则函数g(x)=a+b 的
图象大致是( D )
自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
A
7 8 9 10 11 12 13 14
D
C
B
解 析 :D 由 f(x)的图象可知O
∴g(x) 的图象应为D.
随 堂 检 测 内化素养 1 课时作业分层自检
合作探究深化提能
1 23 4 5 6 7 8 9 10 11 12 13 14
自主阅读新知预习
48
11.设偶函数f(x)=logax-b| 在(一一,0)上单调递增,则f(a+1) 与f(b+2) 的大小关系
是( D )
A.f(a+1)
C.f(a+1)≥f(b+2)
D.f(a+1)>f(b+2)
49 自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
1 2 3 4 5 6 7 8 9 10 ll 12 13 14
解析: D 因为函数f(x)是偶函数,所以b=0,
又函数在(-0,0)上单调递增,所以函数在(0,+一)上单调递减,则0
且1
50 自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
1 23 4 5 6 7 8 9 10 ll 12 13 14
51 自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
12 . 已知f(x) 是定义在R 上的偶函数,且在[0,十一]上单调递增, 则不等式
的解集为 .
解 析 :∵f(x) 是 R 上的偶函数,
∴它的图象关于y 轴对称 .
∵f(x)在[0,十]上单调递增,
∴f(x)在[一一,0]上单调递减,
由 得 则函数的大致图象如图所示.
1 2 3 4 5 6 7 8 9 10 11 12 13 14
或
解得x>2 或
52 自主阅读新知预习合作探究深化提能 随堂检测内化素养课时作业分层自检
1 2 3 4 8 10 1112 13 14
∴原不
答案:
: ·
6 5 工
y
X
0
1
53 自主阅读新知预习合作探究深化提能0 随堂检测内化素养课时作业分层自检
13.已知 的值域为R, 那么实数a 的取值范围是_
解 析 :要使函数f(x)的值域为R,
则必须满
所以
答案:
12 13 14
14.若不等式x —logx<0 内恒成立,求实数m 的取值范围.
解 :由 x -log,x<0, 得 x
要使x
探索创新练
1 2 3 4 5 6 7 8 10 11 12 1314
yA
1
0
1
2
X
55 自主阅读新知预习合作探究 深化提能 随堂检测内化素养课时作业分层自检
即实数m 的取值范围
∵当 时,
∴只要当
即 .又0
即可,
本部分内容讲解结束
合作探究深化提能
随堂检测内化素养
自主阅读新知预习
课时作业分层自检
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
