5.1.2 弧度制-【新教材】人教A版(2019)高中数学必修第一册课件(共21张PPT)
文档属性
| 名称 | 5.1.2 弧度制-【新教材】人教A版(2019)高中数学必修第一册课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 773.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-05 18:12:32 | ||
图片预览








文档简介
(共21张PPT)
第五章 三角函数
5.1.2弧度制
1.理解弧度制的概念;
2.熟练弧度制与角度制的转换
3.掌握弧长公式与扇形的面积公式。
立德树人和谐发展
学习目标
1、在平面几何中研究角的度量时,1°的
角是 义的
周角的 做1度角,记为1°
2、角度制下弧长公式与扇形面积公式是 什么
立德树人和谐发展
复习回顾
我们把用度做单位来度量角的制度叫做角 度制,在数学和其他许多科学研究中还要经常 用到一种度量角的制度—弧度制,它是如何定 义呢
立德树人和谐发展
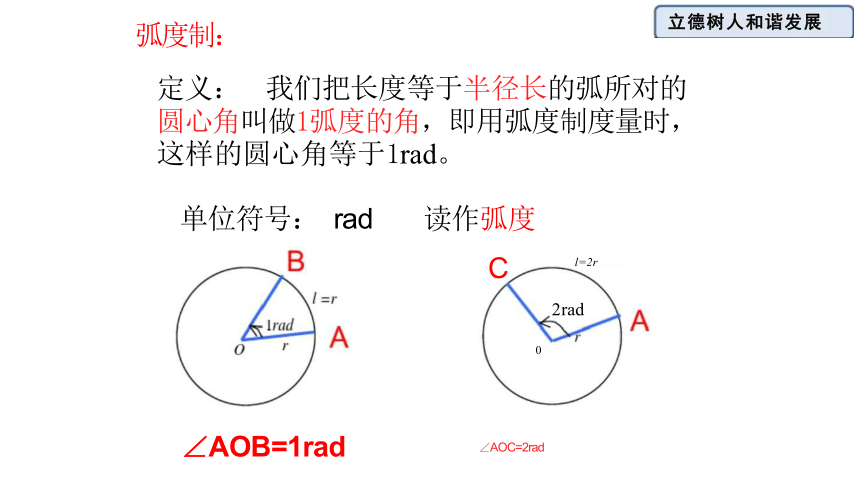
定义: 我们把长度等于半径长的弧所对的 圆心角叫做1弧度的角,即用弧度制度量时, 这样的圆心角等于1rad。
单位符号: rad 读作弧度
∠AOB=1rad ∠AOC=2rad
立德树人和谐发展
l=2r
2rad
0
弧度制:
C
追问4 (1)我们把半径为1的圆叫做单位圆.既然角的大小与半径
无关,那么在单位圆中如何确定1 rad的角呢
(2)在半径为r 的圆中,弧长为l的弧所对的圆心角α的弧度数是多少
(3)角有正、负、零角之分,它的弧度数呢
得出单位圆中长度为1的弧所对的圆心角就是1 rad(如图);
在半径为r 的圆中
类比角度制,α的正负由角α的终边的旋转方向决定.
立德树人和谐发展
新知探究
■
新知探究 立德树人和谐发展
追问5 请你说说弧度制与角度制有哪些不同
第一,弧度制以线段长度来度量角,角度制是“以角量角”;
第二,弧度制是十进制,角度制是六十进制;
第三,1弧度是等于半径长的弧所对的圆心角的大小,而1°的角是周
角的 ■
第四,无论是以“弧度”还是以“度”为单位,角的大小都是一个与半
径大小无关的定值,等等.
360°=2π rad 180°=π rad
问题3 既然角度制、弧度制都是角的度量制,那么,它们
之间如何换算 你认为在换算的过程中最为关键的是什么
立德树人和谐发展
新知探究
例 1 按照下列要求,把67°30'化成弧度: (1)精确值; (2)精确到0.001的近似值.
解:(1)由于6
5
(2)利用计算器有67°30'≈1.178 rad.
立德树人 和谐发展
新知探究
解 :利用计算器有3.14 rad≈179.909°
例2 将3.14 rad换算成角度(用度数表示,精确到0.001)
立德树人和谐发展
新知探究
角 度 ) 50 180
弧 度 π 兀 兀 π 2π 3π 5π 6 兀 3π
2π
注意:今后在具体运算时,“弧度”二字 和单位符号“rad” 可以省略如:3表示 3rad
写出一些特殊角的弧度数
立德树人和谐发展
例3 利用弧度制证明下列关于扇形的公式:
(1)l=aR; (2) ; (3) ■
其中R是圆的半径,a(0积 .
证明:(1)由公式 可得l=aR.
下面证明(2)(3) .
立德树人和谐发展
新知探究
证明:圆心角为n° 的扇形的弧长公式和面积公式分别是 将 n° 转换为弧度,得 ,于是 将l=aR 代入上式,即得
例3 利用弧度制证明下列关于扇形的公式:
(1)l=aR; (2) (3)
其中R是圆的半径,a(0积 .
立德树人和谐发展
新知探究
■
角度制
弧度制
弧长公式
l=|α|R
扇形面积公式
显然,弧度制下的弧长公式和扇形面积公式简单了.在今后的学习中,我们还将
进一步看到弧度制带来的便利.
【1】若用R表示圆的半径,α(O<α<2π)为圆心角,l 是扇形弧长,S是扇形面积.
则有:
弧长公式与扇形面积公式
立德树人和谐发展
(1)l=αR (
(
(4)你能画一个知识结构图来反映本节课的研究内容与路径吗
背景 引入弧度制的必要性 定义的合理性 弧度制
问题4 通过本节课的学习,你学会用弧度制度量角了吗
应 用
关 系
表 示
定 义
立德树人和谐发展
归纳小结
作业A
1. 第175页习题5.1第1,2,3题。
2 .金版 P115-P116.
立德树人和谐发展
课后作业
【1】把下列角度化成弧度:
(1)22°30'; (2)—210°; (3)1200°
立德树人和谐发展
P175 练习
答案: (1)
(2)
(3)
■
■
;
答案:(1)15°; (2)-240°; (3)54°
【2】把下列弧度化成角度:
立德树人和谐发展
P175 练 习
(3)
(1)
(2)
■
;
;
【解】(1){a|a=2kπ,k∈Z}U{a|α=2kπ+kπ,k∈Z}
={α|α=nπ,k∈Z}
(2){a|a=2kπ+",k∈z}u{a|α=2kπ+32,k∈z}
【3】用弧度表示:
(1)终边在x (2)终边在y
轴上的角的集合
轴上的角的集合
是 骡是马遛
立德树人和谐发展
P175 练 习
【5】已知半径为120 mm的圆上,有一条弧的长是144 mm, 求该
弧所对的圆心角(正角)的弧度数.
立德树人和谐发展
答案: 弧度数为1.2.
P175 练习
例4:已知一半径为R 的扇形,它的周长等于所
在圆的周长,那么扇形的中心角是多少弧度
合多少度 扇形的面积是多少
解:周长=2πR=2R+l, 所 以l=2(π—1)R.
所以扇形的中心角是2(π—1)rad.
扇形面积是(π-1)R
立德树人和谐发展
第五章 三角函数
5.1.2弧度制
1.理解弧度制的概念;
2.熟练弧度制与角度制的转换
3.掌握弧长公式与扇形的面积公式。
立德树人和谐发展
学习目标
1、在平面几何中研究角的度量时,1°的
角是 义的
周角的 做1度角,记为1°
2、角度制下弧长公式与扇形面积公式是 什么
立德树人和谐发展
复习回顾
我们把用度做单位来度量角的制度叫做角 度制,在数学和其他许多科学研究中还要经常 用到一种度量角的制度—弧度制,它是如何定 义呢
立德树人和谐发展
定义: 我们把长度等于半径长的弧所对的 圆心角叫做1弧度的角,即用弧度制度量时, 这样的圆心角等于1rad。
单位符号: rad 读作弧度
∠AOB=1rad ∠AOC=2rad
立德树人和谐发展
l=2r
2rad
0
弧度制:
C
追问4 (1)我们把半径为1的圆叫做单位圆.既然角的大小与半径
无关,那么在单位圆中如何确定1 rad的角呢
(2)在半径为r 的圆中,弧长为l的弧所对的圆心角α的弧度数是多少
(3)角有正、负、零角之分,它的弧度数呢
得出单位圆中长度为1的弧所对的圆心角就是1 rad(如图);
在半径为r 的圆中
类比角度制,α的正负由角α的终边的旋转方向决定.
立德树人和谐发展
新知探究
■
新知探究 立德树人和谐发展
追问5 请你说说弧度制与角度制有哪些不同
第一,弧度制以线段长度来度量角,角度制是“以角量角”;
第二,弧度制是十进制,角度制是六十进制;
第三,1弧度是等于半径长的弧所对的圆心角的大小,而1°的角是周
角的 ■
第四,无论是以“弧度”还是以“度”为单位,角的大小都是一个与半
径大小无关的定值,等等.
360°=2π rad 180°=π rad
问题3 既然角度制、弧度制都是角的度量制,那么,它们
之间如何换算 你认为在换算的过程中最为关键的是什么
立德树人和谐发展
新知探究
例 1 按照下列要求,把67°30'化成弧度: (1)精确值; (2)精确到0.001的近似值.
解:(1)由于6
5
(2)利用计算器有67°30'≈1.178 rad.
立德树人 和谐发展
新知探究
解 :利用计算器有3.14 rad≈179.909°
例2 将3.14 rad换算成角度(用度数表示,精确到0.001)
立德树人和谐发展
新知探究
角 度 ) 50 180
弧 度 π 兀 兀 π 2π 3π 5π 6 兀 3π
2π
注意:今后在具体运算时,“弧度”二字 和单位符号“rad” 可以省略如:3表示 3rad
写出一些特殊角的弧度数
立德树人和谐发展
例3 利用弧度制证明下列关于扇形的公式:
(1)l=aR; (2) ; (3) ■
其中R是圆的半径,a(0
证明:(1)由公式 可得l=aR.
下面证明(2)(3) .
立德树人和谐发展
新知探究
证明:圆心角为n° 的扇形的弧长公式和面积公式分别是 将 n° 转换为弧度,得 ,于是 将l=aR 代入上式,即得
例3 利用弧度制证明下列关于扇形的公式:
(1)l=aR; (2) (3)
其中R是圆的半径,a(0
立德树人和谐发展
新知探究
■
角度制
弧度制
弧长公式
l=|α|R
扇形面积公式
显然,弧度制下的弧长公式和扇形面积公式简单了.在今后的学习中,我们还将
进一步看到弧度制带来的便利.
【1】若用R表示圆的半径,α(O<α<2π)为圆心角,l 是扇形弧长,S是扇形面积.
则有:
弧长公式与扇形面积公式
立德树人和谐发展
(1)l=αR (
(
(4)你能画一个知识结构图来反映本节课的研究内容与路径吗
背景 引入弧度制的必要性 定义的合理性 弧度制
问题4 通过本节课的学习,你学会用弧度制度量角了吗
应 用
关 系
表 示
定 义
立德树人和谐发展
归纳小结
作业A
1. 第175页习题5.1第1,2,3题。
2 .金版 P115-P116.
立德树人和谐发展
课后作业
【1】把下列角度化成弧度:
(1)22°30'; (2)—210°; (3)1200°
立德树人和谐发展
P175 练习
答案: (1)
(2)
(3)
■
■
;
答案:(1)15°; (2)-240°; (3)54°
【2】把下列弧度化成角度:
立德树人和谐发展
P175 练 习
(3)
(1)
(2)
■
;
;
【解】(1){a|a=2kπ,k∈Z}U{a|α=2kπ+kπ,k∈Z}
={α|α=nπ,k∈Z}
(2){a|a=2kπ+",k∈z}u{a|α=2kπ+32,k∈z}
【3】用弧度表示:
(1)终边在x (2)终边在y
轴上的角的集合
轴上的角的集合
是 骡是马遛
立德树人和谐发展
P175 练 习
【5】已知半径为120 mm的圆上,有一条弧的长是144 mm, 求该
弧所对的圆心角(正角)的弧度数.
立德树人和谐发展
答案: 弧度数为1.2.
P175 练习
例4:已知一半径为R 的扇形,它的周长等于所
在圆的周长,那么扇形的中心角是多少弧度
合多少度 扇形的面积是多少
解:周长=2πR=2R+l, 所 以l=2(π—1)R.
所以扇形的中心角是2(π—1)rad.
扇形面积是(π-1)R
立德树人和谐发展
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
