8.6.1直线与直线垂直-人教A版(2019)高中数学必修第二册课件(共36张PPT)
文档属性
| 名称 | 8.6.1直线与直线垂直-人教A版(2019)高中数学必修第二册课件(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-05 18:15:05 | ||
图片预览











文档简介
(共36张PPT)
第八章立体几何初步
8.6 空间直线、平面的垂直
8.6.1 直线与直线垂直
学习目标
素养要求
借助长方形,通过直观感知,了解空间中直线与 直线垂直的关系;会用两条异面直线所成角的定 义,找出或作出异面直线所成的角,并求出该角
直观想象、逻辑推理
数学运算
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成| 课后提能训练|
自学导引 课堂互动 素养达成 课后提能训练
数学必修第二册配人版A版 第八章立体几何初步
自学导引|
知识点异面直线所成的角
1. 定义:已知两条异面直线a,b, 经过空间任 意 一点O作直线
a'//a,b′//b, 则异面直线a 与b所成的角就是直线a′ 与 b′ 所成的
锐 角 (或 _直角).
2. 异面直线所成角θ的范围: 0 °<θ≤90°.特别地,当θ= 90 °
时 ,a 与b互相垂直,记作a ⊥b .
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成 课后提能训练
【预习自测】
如图,正方体ABCD-A'B′C′D′ 中异面直线
A′B′ 与BC 所成的角为 .异面直线AD′ 与
BC 所成的角为
【答案】90° 45°
【解析】∵A′B′//AB,∴∠AB C为A'B′ 与BC所成的角,又
∠ABC=90°∴A'B′ 与 BC所成的角为90°.∵BC//AD,∴∠D′AD 为
AD′ 与BC 所成的角.∵∠ D′A D=45°, 故AD′ 与BC 所成的角为45°.
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成 课后提能训练|
数学必修第二册配人版A版 第八章立体几何初步
|课堂互动
自学导引 课堂互动 素养达成| 课后提能训练
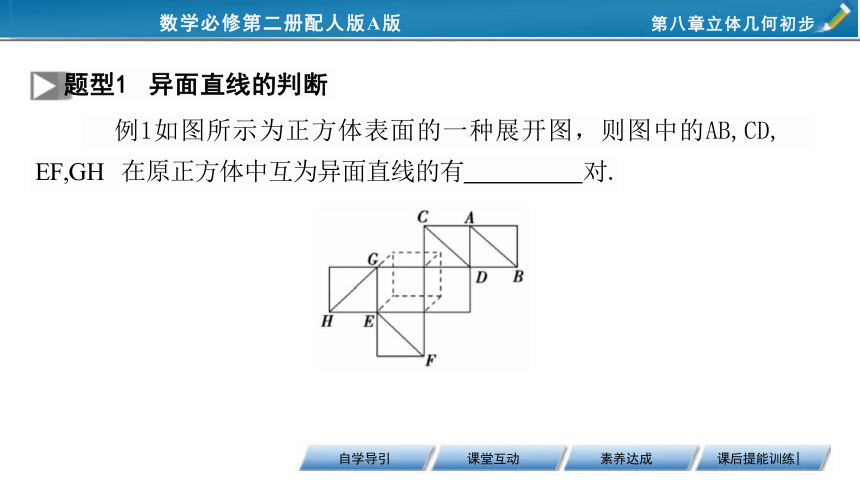
题型1 异面直线的判断
例1如图所示为正方体表面的一种展开图,则图中的AB,CD,
EF,GH 在原正方体中互为异面直线的有 对.
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成 课后提能训练|
素养点睛:本题考查了直观想象的核心素养.
【答案】3
【解析】平面图形的翻折应注意翻折前后相对位置的变化,则AB,
CD,EF 和GH 在原正方体中,显然AB与CD,EF 与GH,AB 与GH 都是异 面直线,而AB与EF 相交,CD 与GH 相 交 ,CD 与EF 平行.故互为异面直 线的有3对.
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成 课后提能训练
规律方法一
异面直线的判定方法
(1)定理:平面外一点A与平面内一点B的连线和平面内不经过点B的
直线是异面直线.
(2)先假设两条直线不是异面直线,即两条直线平行或相交,由假设
出发,经过严格的推理,导出矛盾,从而否定假设,肯定两条直线异 面.此法在异面直线的判定中经常用到.
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成 课后提能训练
数学必修第二册配人版A版
跟踪训练
1.下面四个命题:
①若直线a,b 异面,b,c 异面,则a,c 异面;
②若直线a,b 相交,b,c 相交,则a,c 相交;
③若a,b 为异面直线,直线c//a, 则c与b异面;
④若空间三条直线满足a⊥b,b//c, 则a⊥c. 其中真命题的序号为
自学导引 课堂互动 素养达成 课后提能训练
第八章立体几何初步
【答案】④
【解析】①若直线a,b 异 面 ,b,c 异面,则a,c 三种位置关系都有, 所以①不正确;②若直线a,b 相 交 ,b,c 相交,则a,c 三种位置关系都 有,所以②不正确;③由空间直线的位置关系和c与b可能异面或相交, 所以③不正确;④因为a ⊥b,b//c, 所以a ⊥c, 所以④正确.
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成 课后提能训练
题型2 异面直线所成的角
例2 如图,在正方体ABCD-EFGH中,O为侧面ADHE的中心.
数学必修第二册配人版A版 第八章立体几何初步
求:(1)BE 与CG 所成的角;
(2)FO 与BD 所成的角.
自学导引 课堂互动 素养达成 课后提能训练
解 :(1 )如图,因为CG// BF,
所以∠EBF(或其补角)为异面直线BE与CG所成的角.
又在△BEF中,∠EBF=45°, 所以BE与CG所成的角为45°
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成 课后提能训练
(2)连接FH, 因为HD//EA,EA//FB, 所以HD//FB.
又HD=FB, 所以四边形HFBD为平行四边形.
所以HF//BD, 所以∠HFO (或其补角)为异面直线FO与BD所成的
角 .
连接HA,AF, 易 得FH=HA=AF, 所以△AFH为等边三角形.
又知0为AH的中点,所以∠HFO=30°, 即FO与BD所成的角为30°.
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成 课后提能训练
【例题迁移1】 (变换条件)在本例正方体中,若P
是平面EFGH的中心,其他条件不变,求OP和CD所成的 E< 角.
解 :连接EG,HF, 则P为HF的中点.连接AF,AH ,
则OP//AF.
又CD//AB, 所以∠BAF(或其补角)为异面直线OP与
CD所成的角.
由于△ABF 是等腰直角三角形,所以∠BAF=45°.
故OP与CD所成的角为45°.
自学导引 课堂互动 素养达成 课后提能训练
第八章立体几何初步
数学必修第二册配人版A版
【例题迁移2】 (变换条件)在本例正方体中,若M,N 分别是BF,
CG的中点,且AG和BN所成的角为θ,求AM和BN所成的角.
素养点睛:本题考查了直观想象和数学运算的核心素养.
解:连 接MG.因为四边形BCGF 是正方形,所以BF4CG. 因为M,N 分别是BF,CG 的中点,所以BMNG.
所以四边形BNGM是平行四边形.
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成 课后提能训练
所以BN//MG. 所以∠AGM (或其补角)是异面直线AG 和BN 所成的角,
∠AMG(或其补角)是异面直线AM和BN所成的角.
因为AM=MG, 所以∠AGM=∠MAG=θ.
所以∠AMG=180°-20, 即 AM和BN所成的角为180°-(180°-20)=
20.
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成 课后提能训练|
数学必修第二册配人版A版 第八章立体几何初步
规律方法-
求异面直线所成的角的步骤
(1)找出(或作出)适合题设的角,遇题设中有中点,常考虑中位线;
若异面直线依附于某几何体,且对异面直线平移有困难时,可利用该几 何体的特殊点,使异面直线转化为相交直线.
(2)求——转化为求一个三角形的内角,通过解三角形,求出所找的
角 .
(3)结论——设由(2)所求得的角的大小为0.若0°<θ≤90°,则θ为所求
若90°<θ<180°,则180°-θ为所求.
自学导引 课堂互动 素养达成 课后提能训练|
[提醒]求异面直线所成的角,通常把异面直线平移到同一个三角
形中去,通过解三角形求得,但要注意异面直线所成的角θ的范围是0° <θ≤90°.
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成| 课后提能训练
2. 如图所示,在三棱锥A-BCD 中 ,AB=CD,AB⊥CD,E,F
为BC,AD 的中点,求EF 与AB所成的角.
自学导引 课堂互动 素养达成 课后提能训练
数学必修第二册配人版A版 第八章立体几何初步
跟踪训练
分别
所以∠GFE (或其补角)就是异面直线EF 与AB 所成的角,且EG=GF.
因为AB⊥CD, 所以EG⊥GF.所以∠EGF=90°.
所以△EFG 为等腰直角三角形.
所以∠GFE=45°, 即 EF 与AB所成的角为45°.
解:如图所示,取BD 的中点G, 连 接EG,FG.
因为E,F 分别为BC,AD 的中点,AB=CD, 所以 EG//CD,GF
自学导引 课堂互动 素养达成 课后提能训练
第八章立体几何初步
数学必修第二册配人版A版
//AB, 且
事
3 .在正方体ABCD-A B C D 中,求A B与B D 所成的角.
解 :如图,连接BD,A D.∵ABCD-A B C D 是正方体,
自学导引 课堂互动 素养达成 课后提能训练|
数学必修第二册配人版A版 第八章立体几何初步
∴DD //BB .又DD =BB ,
∴四边形DBB D 为平行四边形,∴BD//B D .∵A B,BD,A D 是
全等的正方形的对角线,∴A B=BD=A D , 则△A BD是正三角形,
∴∠A BD=60°.
∵∠A BD 是锐角,∴∠A BD 是异面直线A B 与B D 所成的角,即
A B与B D 所成的角为60°
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成 课后提能训练|
数学必修第二册配人版A版 第八章立体几何初步
易错警示 忽略空间角的范围致误
例3如图,已知空间四边形ABCD 中,AD=BC,M,N 分别为AB,
CD的中点,且直线BC与MN所成的角为30°,则BC与AD所成的角为
自学导引 课堂互动 素养达成 课后提能训练|
数学必修第二册配人版A版 第八章立体几何初步
错解: 120°
如图,连接BD, 并取中点E, 连接EN,EM, 则EN//BC,ME//AD,
故∠ENM为BC与MN所成的角,∠MEN为BC与AD所成的角,∴∠ENM
=30°.又由AD=BC, 知ME=EN, ∴∠ EMN=∠ ENM=30°,
∴∠MEN=180°—30°—30°=120°, 即BC 与AD 所成的角为120°
自学导引 课堂互动 素养达成 课后提能训练
易错防范: 在未判断出∠MEN 是锐角或直角还是钝角之前,不能断
定它就是两异面直线所成的角,因为异面直线所成的角α的取值范围是 0°正解:易求得∠MEN=120°, 又 ∠MEN(或其补角)是BC与AD所成
的角,∴BC与AD所成的角为60°.
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成 课后提能训练
数学必修第二册配人版A版 第八章立体几何初步
素养达成
自学导引 课堂互动 素养达成| 课后提能训练
课堂 归纳
在研究异面直线所成角的大小时,通常把两条异面直线所成的角转
化为两条相交直线所成的角.将空间问题向平面问题转化,这是我们学 习立体几何的一条重要的思维途径.需要强调的是,两条异面直线所成
角的范围为(0°,90°),解题时经常结合这一点去求异面直线所成角的
大小(体现直观想象与数学运算的核心素养).
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成 课后提能训练
素养训练
1. 如果两条直线a 和b没有公共点,那么a 与b的位置关系是( )
A. 共面 B. 平 行
C. 异面 D. 平行或异面
【答案】D
【解析】由两条直线的位置关系,可知答案为D.
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成 课后提能训练|
2. 设α为两条异面直线所成的角,则α满足 ( )
A.0°C.0°≤a≤90° D.0°【答案】B
【解析】异面直线所成的角为锐角或直角.故选B.
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成 课后提能训练|
3. 已知两条直线a,b, 且a// 平面α,bca, 则a 与b的位置关系是
【答案】平行或异面
【解析】a //a, 则 a与α无交点,bca, 则 a与b无交点,所以a,b 是 平行或异面.
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成 课后提能训练
4.如图所示,正方体ABCD-A B C D 中 ,E,F 分别是棱BC,CC
的中点,则异面直线EF与B D 所成的角为 .
自学导引 课堂互动 素养达成 课后提能训练
数学必修第二册配人版A版 第八章立体几何初步
【答案】60°
数学必修第二册配人版A版 第八章立体几何初步
【解析】连接BC ,AD ,AB , 则EF为△BCC 的中位线,
∴EF//BC .∵AB//CD//C D , 且AB=CD=C D ,∴ 四边形ABC D 为 平行四边形 .∴BC //AD ∴EF//AD .
∴∠AD B 为异面直线EF和B D 所成的角或其补角.在△AB D 中 ,
易知AB =B D =AD ,∴△AB D 为正三角形,∴∠AD B =60° .
自学导引 课堂互动 素养达成 课后提能训练|
∴EF与B D 所成的角为60° .
5. 如图所示,点A 是△BCD 所在平面外一点,AD=BC,E,F 分
别是AB,CD 的中点,当 时,求异面直线AD 和 BC 所成的
自学导引 课堂互动 素养达成 课后提能训练
数学必修第二册配人版A版 第八章立体几何初步
角 .
数学必修第二册配人版A版 第八章立体几何初步
∵E,F,G 分别为AB,CD,AC
∴EG//BC, 且
解:如图所示,设G 为AC 的中点,连接EG,FG.
自学导引 课堂互动 素养达成 课后提能训练
FG//AD,且
的中点,
∴EG 与 GF 所成的锐角(或直角)即为AD 与 BC 所成的角.
在△EFG中,∵ 事
∴EG +FG =EF , 即EG⊥FG.
∴∠EGF=90°.故 AD 与BC 所成角为90°.
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成 课后提能训练
又AD=BC,∴
第八章立体几何初步
8.6 空间直线、平面的垂直
8.6.1 直线与直线垂直
学习目标
素养要求
借助长方形,通过直观感知,了解空间中直线与 直线垂直的关系;会用两条异面直线所成角的定 义,找出或作出异面直线所成的角,并求出该角
直观想象、逻辑推理
数学运算
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成| 课后提能训练|
自学导引 课堂互动 素养达成 课后提能训练
数学必修第二册配人版A版 第八章立体几何初步
自学导引|
知识点异面直线所成的角
1. 定义:已知两条异面直线a,b, 经过空间任 意 一点O作直线
a'//a,b′//b, 则异面直线a 与b所成的角就是直线a′ 与 b′ 所成的
锐 角 (或 _直角).
2. 异面直线所成角θ的范围: 0 °<θ≤90°.特别地,当θ= 90 °
时 ,a 与b互相垂直,记作a ⊥b .
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成 课后提能训练
【预习自测】
如图,正方体ABCD-A'B′C′D′ 中异面直线
A′B′ 与BC 所成的角为 .异面直线AD′ 与
BC 所成的角为
【答案】90° 45°
【解析】∵A′B′//AB,∴∠AB C为A'B′ 与BC所成的角,又
∠ABC=90°∴A'B′ 与 BC所成的角为90°.∵BC//AD,∴∠D′AD 为
AD′ 与BC 所成的角.∵∠ D′A D=45°, 故AD′ 与BC 所成的角为45°.
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成 课后提能训练|
数学必修第二册配人版A版 第八章立体几何初步
|课堂互动
自学导引 课堂互动 素养达成| 课后提能训练
题型1 异面直线的判断
例1如图所示为正方体表面的一种展开图,则图中的AB,CD,
EF,GH 在原正方体中互为异面直线的有 对.
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成 课后提能训练|
素养点睛:本题考查了直观想象的核心素养.
【答案】3
【解析】平面图形的翻折应注意翻折前后相对位置的变化,则AB,
CD,EF 和GH 在原正方体中,显然AB与CD,EF 与GH,AB 与GH 都是异 面直线,而AB与EF 相交,CD 与GH 相 交 ,CD 与EF 平行.故互为异面直 线的有3对.
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成 课后提能训练
规律方法一
异面直线的判定方法
(1)定理:平面外一点A与平面内一点B的连线和平面内不经过点B的
直线是异面直线.
(2)先假设两条直线不是异面直线,即两条直线平行或相交,由假设
出发,经过严格的推理,导出矛盾,从而否定假设,肯定两条直线异 面.此法在异面直线的判定中经常用到.
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成 课后提能训练
数学必修第二册配人版A版
跟踪训练
1.下面四个命题:
①若直线a,b 异面,b,c 异面,则a,c 异面;
②若直线a,b 相交,b,c 相交,则a,c 相交;
③若a,b 为异面直线,直线c//a, 则c与b异面;
④若空间三条直线满足a⊥b,b//c, 则a⊥c. 其中真命题的序号为
自学导引 课堂互动 素养达成 课后提能训练
第八章立体几何初步
【答案】④
【解析】①若直线a,b 异 面 ,b,c 异面,则a,c 三种位置关系都有, 所以①不正确;②若直线a,b 相 交 ,b,c 相交,则a,c 三种位置关系都 有,所以②不正确;③由空间直线的位置关系和c与b可能异面或相交, 所以③不正确;④因为a ⊥b,b//c, 所以a ⊥c, 所以④正确.
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成 课后提能训练
题型2 异面直线所成的角
例2 如图,在正方体ABCD-EFGH中,O为侧面ADHE的中心.
数学必修第二册配人版A版 第八章立体几何初步
求:(1)BE 与CG 所成的角;
(2)FO 与BD 所成的角.
自学导引 课堂互动 素养达成 课后提能训练
解 :(1 )如图,因为CG// BF,
所以∠EBF(或其补角)为异面直线BE与CG所成的角.
又在△BEF中,∠EBF=45°, 所以BE与CG所成的角为45°
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成 课后提能训练
(2)连接FH, 因为HD//EA,EA//FB, 所以HD//FB.
又HD=FB, 所以四边形HFBD为平行四边形.
所以HF//BD, 所以∠HFO (或其补角)为异面直线FO与BD所成的
角 .
连接HA,AF, 易 得FH=HA=AF, 所以△AFH为等边三角形.
又知0为AH的中点,所以∠HFO=30°, 即FO与BD所成的角为30°.
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成 课后提能训练
【例题迁移1】 (变换条件)在本例正方体中,若P
是平面EFGH的中心,其他条件不变,求OP和CD所成的 E< 角.
解 :连接EG,HF, 则P为HF的中点.连接AF,AH ,
则OP//AF.
又CD//AB, 所以∠BAF(或其补角)为异面直线OP与
CD所成的角.
由于△ABF 是等腰直角三角形,所以∠BAF=45°.
故OP与CD所成的角为45°.
自学导引 课堂互动 素养达成 课后提能训练
第八章立体几何初步
数学必修第二册配人版A版
【例题迁移2】 (变换条件)在本例正方体中,若M,N 分别是BF,
CG的中点,且AG和BN所成的角为θ,求AM和BN所成的角.
素养点睛:本题考查了直观想象和数学运算的核心素养.
解:连 接MG.因为四边形BCGF 是正方形,所以BF4CG. 因为M,N 分别是BF,CG 的中点,所以BMNG.
所以四边形BNGM是平行四边形.
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成 课后提能训练
所以BN//MG. 所以∠AGM (或其补角)是异面直线AG 和BN 所成的角,
∠AMG(或其补角)是异面直线AM和BN所成的角.
因为AM=MG, 所以∠AGM=∠MAG=θ.
所以∠AMG=180°-20, 即 AM和BN所成的角为180°-(180°-20)=
20.
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成 课后提能训练|
数学必修第二册配人版A版 第八章立体几何初步
规律方法-
求异面直线所成的角的步骤
(1)找出(或作出)适合题设的角,遇题设中有中点,常考虑中位线;
若异面直线依附于某几何体,且对异面直线平移有困难时,可利用该几 何体的特殊点,使异面直线转化为相交直线.
(2)求——转化为求一个三角形的内角,通过解三角形,求出所找的
角 .
(3)结论——设由(2)所求得的角的大小为0.若0°<θ≤90°,则θ为所求
若90°<θ<180°,则180°-θ为所求.
自学导引 课堂互动 素养达成 课后提能训练|
[提醒]求异面直线所成的角,通常把异面直线平移到同一个三角
形中去,通过解三角形求得,但要注意异面直线所成的角θ的范围是0° <θ≤90°.
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成| 课后提能训练
2. 如图所示,在三棱锥A-BCD 中 ,AB=CD,AB⊥CD,E,F
为BC,AD 的中点,求EF 与AB所成的角.
自学导引 课堂互动 素养达成 课后提能训练
数学必修第二册配人版A版 第八章立体几何初步
跟踪训练
分别
所以∠GFE (或其补角)就是异面直线EF 与AB 所成的角,且EG=GF.
因为AB⊥CD, 所以EG⊥GF.所以∠EGF=90°.
所以△EFG 为等腰直角三角形.
所以∠GFE=45°, 即 EF 与AB所成的角为45°.
解:如图所示,取BD 的中点G, 连 接EG,FG.
因为E,F 分别为BC,AD 的中点,AB=CD, 所以 EG//CD,GF
自学导引 课堂互动 素养达成 课后提能训练
第八章立体几何初步
数学必修第二册配人版A版
//AB, 且
事
3 .在正方体ABCD-A B C D 中,求A B与B D 所成的角.
解 :如图,连接BD,A D.∵ABCD-A B C D 是正方体,
自学导引 课堂互动 素养达成 课后提能训练|
数学必修第二册配人版A版 第八章立体几何初步
∴DD //BB .又DD =BB ,
∴四边形DBB D 为平行四边形,∴BD//B D .∵A B,BD,A D 是
全等的正方形的对角线,∴A B=BD=A D , 则△A BD是正三角形,
∴∠A BD=60°.
∵∠A BD 是锐角,∴∠A BD 是异面直线A B 与B D 所成的角,即
A B与B D 所成的角为60°
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成 课后提能训练|
数学必修第二册配人版A版 第八章立体几何初步
易错警示 忽略空间角的范围致误
例3如图,已知空间四边形ABCD 中,AD=BC,M,N 分别为AB,
CD的中点,且直线BC与MN所成的角为30°,则BC与AD所成的角为
自学导引 课堂互动 素养达成 课后提能训练|
数学必修第二册配人版A版 第八章立体几何初步
错解: 120°
如图,连接BD, 并取中点E, 连接EN,EM, 则EN//BC,ME//AD,
故∠ENM为BC与MN所成的角,∠MEN为BC与AD所成的角,∴∠ENM
=30°.又由AD=BC, 知ME=EN, ∴∠ EMN=∠ ENM=30°,
∴∠MEN=180°—30°—30°=120°, 即BC 与AD 所成的角为120°
自学导引 课堂互动 素养达成 课后提能训练
易错防范: 在未判断出∠MEN 是锐角或直角还是钝角之前,不能断
定它就是两异面直线所成的角,因为异面直线所成的角α的取值范围是 0°
的角,∴BC与AD所成的角为60°.
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成 课后提能训练
数学必修第二册配人版A版 第八章立体几何初步
素养达成
自学导引 课堂互动 素养达成| 课后提能训练
课堂 归纳
在研究异面直线所成角的大小时,通常把两条异面直线所成的角转
化为两条相交直线所成的角.将空间问题向平面问题转化,这是我们学 习立体几何的一条重要的思维途径.需要强调的是,两条异面直线所成
角的范围为(0°,90°),解题时经常结合这一点去求异面直线所成角的
大小(体现直观想象与数学运算的核心素养).
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成 课后提能训练
素养训练
1. 如果两条直线a 和b没有公共点,那么a 与b的位置关系是( )
A. 共面 B. 平 行
C. 异面 D. 平行或异面
【答案】D
【解析】由两条直线的位置关系,可知答案为D.
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成 课后提能训练|
2. 设α为两条异面直线所成的角,则α满足 ( )
A.0°
【解析】异面直线所成的角为锐角或直角.故选B.
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成 课后提能训练|
3. 已知两条直线a,b, 且a// 平面α,bca, 则a 与b的位置关系是
【答案】平行或异面
【解析】a //a, 则 a与α无交点,bca, 则 a与b无交点,所以a,b 是 平行或异面.
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成 课后提能训练
4.如图所示,正方体ABCD-A B C D 中 ,E,F 分别是棱BC,CC
的中点,则异面直线EF与B D 所成的角为 .
自学导引 课堂互动 素养达成 课后提能训练
数学必修第二册配人版A版 第八章立体几何初步
【答案】60°
数学必修第二册配人版A版 第八章立体几何初步
【解析】连接BC ,AD ,AB , 则EF为△BCC 的中位线,
∴EF//BC .∵AB//CD//C D , 且AB=CD=C D ,∴ 四边形ABC D 为 平行四边形 .∴BC //AD ∴EF//AD .
∴∠AD B 为异面直线EF和B D 所成的角或其补角.在△AB D 中 ,
易知AB =B D =AD ,∴△AB D 为正三角形,∴∠AD B =60° .
自学导引 课堂互动 素养达成 课后提能训练|
∴EF与B D 所成的角为60° .
5. 如图所示,点A 是△BCD 所在平面外一点,AD=BC,E,F 分
别是AB,CD 的中点,当 时,求异面直线AD 和 BC 所成的
自学导引 课堂互动 素养达成 课后提能训练
数学必修第二册配人版A版 第八章立体几何初步
角 .
数学必修第二册配人版A版 第八章立体几何初步
∵E,F,G 分别为AB,CD,AC
∴EG//BC, 且
解:如图所示,设G 为AC 的中点,连接EG,FG.
自学导引 课堂互动 素养达成 课后提能训练
FG//AD,且
的中点,
∴EG 与 GF 所成的锐角(或直角)即为AD 与 BC 所成的角.
在△EFG中,∵ 事
∴EG +FG =EF , 即EG⊥FG.
∴∠EGF=90°.故 AD 与BC 所成角为90°.
数学必修第二册配人版A版 第八章立体几何初步
自学导引 课堂互动 素养达成 课后提能训练
又AD=BC,∴
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
