4.3 对数函数的概念 课件(共24张PPT)-高一数学人教A版(2019)必修第一册
文档属性
| 名称 | 4.3 对数函数的概念 课件(共24张PPT)-高一数学人教A版(2019)必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-06 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
第三章函数的概念与性质
4.4 对数函数
4.4.1 对数函数的概念
新教材人教版·高中必修第一册
数学
课标要求
1.理解对数函数的概念.
2.会求与对数函数有关的定义域问题。
3.了解对数函数在生产实际中的简单应用.
素养要求
1.通过对数函数的概念的学习,提升数学抽象素养.
2.借助于对数函数在生产实际中的应用,发展数学建模素 养 .
要求
目录
情景引入
考古学家是如何推测出土文物或古遗址年代的
目录
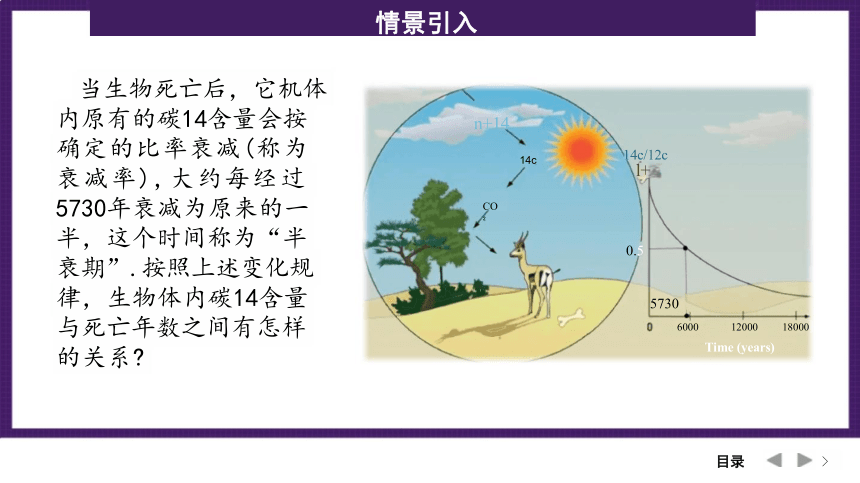
当生物死亡后,它机体 内原有的碳14含量会按 确定的比率衰减(称为 衰减率),大约每经过 5730年衰减为原来的一 半,这个时间称为“半 衰期”.按照上述变化规 律,生物体内碳14含量 与死亡年数之间有怎样 的关系
14c/12c
l+
0.5
5730
6000 12000 18000
Time (years)
情景引入
n+14
14c
目录 >
CO
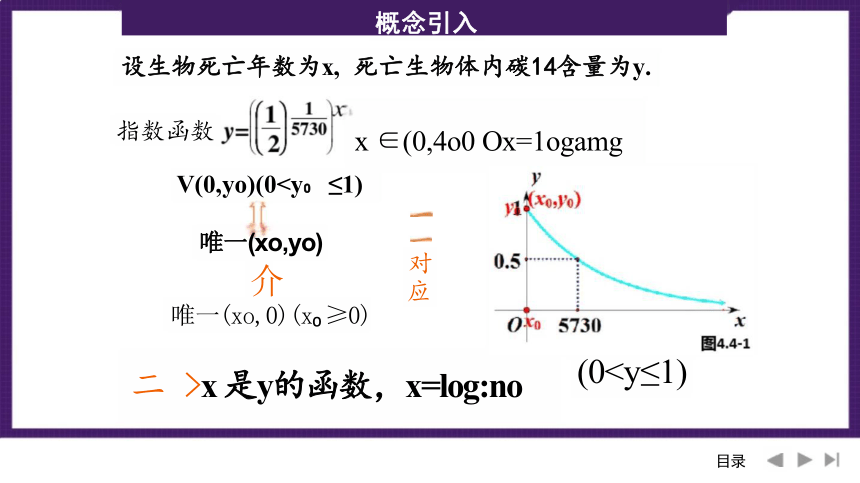
设生物死亡年数为x, 死亡生物体内碳14含量为y.
x ∈(0,+00)
指数函数模型研究了呈指数增长或衰减变化规律的问题。
这个指数函数反应了已知生物死亡的年限,就能计算出 它的碳14含量。而大多数情况下的应用是,已知碳14的 含量,求生物死亡的年数,进而知道死亡的年代。那么 如何来求呢 它又是一个什么样的函数
情景引入
目录
死亡生物体内碳14含量为y.
x ∈(0,4o0 Ox=1ogamg
V(0,yo)(0唯一(xo,yo)
介
唯一(xo,0)(x ≥0)
概念引入
设生物死亡年数为x,
指数函数
二 >x 是y的函数,x=log:no
(0对 应
目录
指数函数y=a (a>0 且a≠1)Dx=logay (a>0且a≠1)
Oy=logax (a>0且a≠1)① 对数函数
一般地,函数 y=logax(a>0, 且 a≠1) 叫 做对数函数
(logarithmic function),其中x 是自变量,定义域是(0,+0o)
概念引入
目录 >
1、 对数函数定义是形式定义,在对数函数的定义表达
式y=logax(a>0, 且 a≠1)中,
①logax 前边的系数必须是1;
②自变量x 在真数的位置上,且只有x;
③底数大于零且不等于1。
④定义域是(0,+0)
否则就不是对数函数。
目录 N
概念理解
2、例如给出下列函数:
;②y=log (x—1);③y=log(x+1)x;④y=—logax(a>0
且a≠1). 其中是对数函数的有( )
A.1 个 B.2 个 C.3 个 D.0 个
概念理解
价化简为对数函数标准形式的,也是对数函数。
满足对数函数的定义,注意可以等
解析 只有第④个
目录
>
解:
(1)因为x >0, 即x≠0,
所以函数y=log x 的定义域是{xlx≠0}.
(2)因为4-x>0, 即x<4,
所以函数 y=loga(4-x)的定义域是{xlx<4}.
例1求下列函数的定义域:
(1)y=log x ; (2)y=loga(4-x)(a>0, 且 a≠1).
巩固与练习
显然两函数
都不是对数函数,
但都与对应的对数函数
有着密切的联系,那么对应
的对数函数的定义域 就是我们解题依据。
目录
例1求下列函数的定义域:
(3)函数 的定义域为 .
解:
(3) 由
解得—1的定义域为
(—1,0)U[0,3].
目录
巩固与练习
规律方法
1.求含对数式的函数定义域关键是真数大于0,
底数大于0且不为1.
2. 若对数出现在分母上时,
真数大于0且不等于1.
巩固与练习
目录
解 (1)由题意可知,经过y 年后物价x 为 x=(1+5%), 即x=1.05V(y∈[0,+00)].
由对数与指数间的关系,可得 y=log1.05X,x∈[1,+00].
由计算工具可得,当x=2 时 ,y≈14.
所以,该地区的物价大约经过14年后会翻一番.
目录
例2假设某地初始物价为1,每年以5%的增长率递增,经过y 年后的
物价为x.
(1)该地的物价经过几年后会翻一番
(2)填写下表,并根据表中的数据,说明该地物价的变化规律.
物价x 1 2 3 4 5 6 7 8 9
10
年数y 0
巩固与练习
例2假设某地初始物价为1,每年以5%的增长率递增,经过y 年后的
物价为x.
(1)该地的物价经过几年后会翻一番
(2)填写下表,并根据表中的数据,说明该地物价的变化规律.
物价x 1 2 3 4 5 6 7 8 9
10
年数y 0
物 价 x 1 2 3 4 5 6 7 8 9
10
年 数 y 0 14 23 28 33 37 40 43 45
47
巩固与练习
(2)根据函数 y=log1.05x,x∈(1,+00), 利用计算工具,可得下表:
目录
例2假设某地初始物价为1,每年以5%的增长率递增,经过y 年后的
物价为x.
(1)该地的物价经过几年后会翻一番
(2)填写下表,并根据表中的数据,说明该地物价的变化规律.
物 价 x 1 2 3 4 5 6 7 8 9 10
年 数 y 0 14 23 28 33 37 40 43 45 47
相邻年 L△ L L L
数差 14 9 5 5 4 3 3 2 2
物价x 1 2 3 4 5 6 7 8 9
10
年数y 0
巩固与练习
(2)根据函数 y=log1.05x,x∈(1,+00), 利用计算工具,可得下表:
目录
例2假设某地初始物价为1,每年以5%的增长率递增,经过y 年后的
物价为x.
(1)该地的物价经过几年后会翻一番
(2)填写下表,并根据表中的数据,说明该地物价的变化规律.
由表中的数据可以发现,该地区的物价随时间的增长而增长,但大约
每增加1倍所需要的时间在逐渐缩小.
目 录
物价x 1 2 3 4 5 6 7 8 9
10
年数y 0
物 价 x 1 2 3 4 5 6 7 8 9
10
年 数 y 0 14 23 28 33 37 40 43 45
47
巩固与练习
(2)根据函数 y=log1.05x,x∈(1,+00), 利用计算工具,可得下表:
解决此类问题时,应根据条件建立数学模型,先利用指数式和
对数式的互化转化为对数式,再根据对数的运算性质及所给的数 据计算求值。
巩固与练习
规律方法
目录
训练1某公司制定了一个激励销售人员的奖励方案:当销售利润不超过10
万元时,按销售利润的15%进行奖励;当销售利润超过10万元时,若超
出A万元,则超出部分按2log (A+1) 进行奖励.记奖金为y(单位:万元),
销售利润为x(单位:万元).
(1)写出奖金y 关于销售利润x 的解析式;
(2)如果业务员老江获得5.5万元的奖金,那么他的销售利润是多少万元
解
(1)由题意知
目录
巩固与练习
训练1某公司制定了一个激励销售人员的奖励方案:当销售利润不超过10
万元时,按销售利润的15%进行奖励;当销售利润超过10万元时,若超 出A万元,则超出部分按2log (A+1) 进行奖励.记奖金为y(单位:万元),
销售利润为x(单位:万元).
(1)写出奖金y 关于销售利润x 的解析式;
(2)如果业务员老江获得5.5万元的奖金,那么他的销售利润是多少万元
(2)由题意知1.5+2log (x—9)=5.5,
即 log (x—9)=2,∴x—9=5 , 解得x=34.
∴老江的销售利润是34万元.
目录
巩固与练习
思考辨析 判断下列说法是否正确,正确的在后面的括号内打
“ √ ”,错误的打“×”.
(1)由y=logax,得x=a, 所 以x>0.(√)
(2)y=log x 是对数函数.(×)
(3)若y=logax 是对数函数,则a>0 且 a≠1.( √)
(4)函数y=loga(x—1)的定义域为(0,十一).(×)
深化思考
目录
>
1、对数函数、指数函数、 一次函数、二次函数是我们学习的基本
初等函数,它们增长是有差异的,不同类型的数据增长应选取合适
的函数模型来刻画其变化规律.
2、判断一个函数是不是对数函数、关键是分析所给函数是否具有
y=logax(a>0, 且 a≠1)这种形式.
3、涉及对数函数的定义域问题,从对数式的真数和底数两个方面
构建不等式组,且最终结果要写成集合的形
小结
目录
1. 下列函数是对数函数的是 (填序号).
①y=loga(5+x)(a>0 且 a≠1);②y=logj-x;③y=log (-x);
④y=logr\3(x>0 且 x≠1).
2.设函数 f(x)=logax(a>0, 且 a≠1), 若f(x x ...X2022)=6, 则 f(x ) 十
f(x )+f(x3)十 . . +f(x2022)的值是 .
3. 已知函数f(x)=Ig(x+1) 一lg(1—x).
(1)求函数f(x)的定义域;(2)判断函数f(x)的奇偶性.
限时小练
[2. 3.
简解答:[ 1.
目录
>
课堂作业
1.教科书第131页练习第2题;
2.课后练习.
目录
本节内容结束THANKS
目录
M
第三章函数的概念与性质
4.4 对数函数
4.4.1 对数函数的概念
新教材人教版·高中必修第一册
数学
课标要求
1.理解对数函数的概念.
2.会求与对数函数有关的定义域问题。
3.了解对数函数在生产实际中的简单应用.
素养要求
1.通过对数函数的概念的学习,提升数学抽象素养.
2.借助于对数函数在生产实际中的应用,发展数学建模素 养 .
要求
目录
情景引入
考古学家是如何推测出土文物或古遗址年代的
目录
当生物死亡后,它机体 内原有的碳14含量会按 确定的比率衰减(称为 衰减率),大约每经过 5730年衰减为原来的一 半,这个时间称为“半 衰期”.按照上述变化规 律,生物体内碳14含量 与死亡年数之间有怎样 的关系
14c/12c
l+
0.5
5730
6000 12000 18000
Time (years)
情景引入
n+14
14c
目录 >
CO
设生物死亡年数为x, 死亡生物体内碳14含量为y.
x ∈(0,+00)
指数函数模型研究了呈指数增长或衰减变化规律的问题。
这个指数函数反应了已知生物死亡的年限,就能计算出 它的碳14含量。而大多数情况下的应用是,已知碳14的 含量,求生物死亡的年数,进而知道死亡的年代。那么 如何来求呢 它又是一个什么样的函数
情景引入
目录
死亡生物体内碳14含量为y.
x ∈(0,4o0 Ox=1ogamg
V(0,yo)(0
介
唯一(xo,0)(x ≥0)
概念引入
设生物死亡年数为x,
指数函数
二 >x 是y的函数,x=log:no
(0
目录
指数函数y=a (a>0 且a≠1)Dx=logay (a>0且a≠1)
Oy=logax (a>0且a≠1)① 对数函数
一般地,函数 y=logax(a>0, 且 a≠1) 叫 做对数函数
(logarithmic function),其中x 是自变量,定义域是(0,+0o)
概念引入
目录 >
1、 对数函数定义是形式定义,在对数函数的定义表达
式y=logax(a>0, 且 a≠1)中,
①logax 前边的系数必须是1;
②自变量x 在真数的位置上,且只有x;
③底数大于零且不等于1。
④定义域是(0,+0)
否则就不是对数函数。
目录 N
概念理解
2、例如给出下列函数:
;②y=log (x—1);③y=log(x+1)x;④y=—logax(a>0
且a≠1). 其中是对数函数的有( )
A.1 个 B.2 个 C.3 个 D.0 个
概念理解
价化简为对数函数标准形式的,也是对数函数。
满足对数函数的定义,注意可以等
解析 只有第④个
目录
>
解:
(1)因为x >0, 即x≠0,
所以函数y=log x 的定义域是{xlx≠0}.
(2)因为4-x>0, 即x<4,
所以函数 y=loga(4-x)的定义域是{xlx<4}.
例1求下列函数的定义域:
(1)y=log x ; (2)y=loga(4-x)(a>0, 且 a≠1).
巩固与练习
显然两函数
都不是对数函数,
但都与对应的对数函数
有着密切的联系,那么对应
的对数函数的定义域 就是我们解题依据。
目录
例1求下列函数的定义域:
(3)函数 的定义域为 .
解:
(3) 由
解得—1
(—1,0)U[0,3].
目录
巩固与练习
规律方法
1.求含对数式的函数定义域关键是真数大于0,
底数大于0且不为1.
2. 若对数出现在分母上时,
真数大于0且不等于1.
巩固与练习
目录
解 (1)由题意可知,经过y 年后物价x 为 x=(1+5%), 即x=1.05V(y∈[0,+00)].
由对数与指数间的关系,可得 y=log1.05X,x∈[1,+00].
由计算工具可得,当x=2 时 ,y≈14.
所以,该地区的物价大约经过14年后会翻一番.
目录
例2假设某地初始物价为1,每年以5%的增长率递增,经过y 年后的
物价为x.
(1)该地的物价经过几年后会翻一番
(2)填写下表,并根据表中的数据,说明该地物价的变化规律.
物价x 1 2 3 4 5 6 7 8 9
10
年数y 0
巩固与练习
例2假设某地初始物价为1,每年以5%的增长率递增,经过y 年后的
物价为x.
(1)该地的物价经过几年后会翻一番
(2)填写下表,并根据表中的数据,说明该地物价的变化规律.
物价x 1 2 3 4 5 6 7 8 9
10
年数y 0
物 价 x 1 2 3 4 5 6 7 8 9
10
年 数 y 0 14 23 28 33 37 40 43 45
47
巩固与练习
(2)根据函数 y=log1.05x,x∈(1,+00), 利用计算工具,可得下表:
目录
例2假设某地初始物价为1,每年以5%的增长率递增,经过y 年后的
物价为x.
(1)该地的物价经过几年后会翻一番
(2)填写下表,并根据表中的数据,说明该地物价的变化规律.
物 价 x 1 2 3 4 5 6 7 8 9 10
年 数 y 0 14 23 28 33 37 40 43 45 47
相邻年 L△ L L L
数差 14 9 5 5 4 3 3 2 2
物价x 1 2 3 4 5 6 7 8 9
10
年数y 0
巩固与练习
(2)根据函数 y=log1.05x,x∈(1,+00), 利用计算工具,可得下表:
目录
例2假设某地初始物价为1,每年以5%的增长率递增,经过y 年后的
物价为x.
(1)该地的物价经过几年后会翻一番
(2)填写下表,并根据表中的数据,说明该地物价的变化规律.
由表中的数据可以发现,该地区的物价随时间的增长而增长,但大约
每增加1倍所需要的时间在逐渐缩小.
目 录
物价x 1 2 3 4 5 6 7 8 9
10
年数y 0
物 价 x 1 2 3 4 5 6 7 8 9
10
年 数 y 0 14 23 28 33 37 40 43 45
47
巩固与练习
(2)根据函数 y=log1.05x,x∈(1,+00), 利用计算工具,可得下表:
解决此类问题时,应根据条件建立数学模型,先利用指数式和
对数式的互化转化为对数式,再根据对数的运算性质及所给的数 据计算求值。
巩固与练习
规律方法
目录
训练1某公司制定了一个激励销售人员的奖励方案:当销售利润不超过10
万元时,按销售利润的15%进行奖励;当销售利润超过10万元时,若超
出A万元,则超出部分按2log (A+1) 进行奖励.记奖金为y(单位:万元),
销售利润为x(单位:万元).
(1)写出奖金y 关于销售利润x 的解析式;
(2)如果业务员老江获得5.5万元的奖金,那么他的销售利润是多少万元
解
(1)由题意知
目录
巩固与练习
训练1某公司制定了一个激励销售人员的奖励方案:当销售利润不超过10
万元时,按销售利润的15%进行奖励;当销售利润超过10万元时,若超 出A万元,则超出部分按2log (A+1) 进行奖励.记奖金为y(单位:万元),
销售利润为x(单位:万元).
(1)写出奖金y 关于销售利润x 的解析式;
(2)如果业务员老江获得5.5万元的奖金,那么他的销售利润是多少万元
(2)由题意知1.5+2log (x—9)=5.5,
即 log (x—9)=2,∴x—9=5 , 解得x=34.
∴老江的销售利润是34万元.
目录
巩固与练习
思考辨析 判断下列说法是否正确,正确的在后面的括号内打
“ √ ”,错误的打“×”.
(1)由y=logax,得x=a, 所 以x>0.(√)
(2)y=log x 是对数函数.(×)
(3)若y=logax 是对数函数,则a>0 且 a≠1.( √)
(4)函数y=loga(x—1)的定义域为(0,十一).(×)
深化思考
目录
>
1、对数函数、指数函数、 一次函数、二次函数是我们学习的基本
初等函数,它们增长是有差异的,不同类型的数据增长应选取合适
的函数模型来刻画其变化规律.
2、判断一个函数是不是对数函数、关键是分析所给函数是否具有
y=logax(a>0, 且 a≠1)这种形式.
3、涉及对数函数的定义域问题,从对数式的真数和底数两个方面
构建不等式组,且最终结果要写成集合的形
小结
目录
1. 下列函数是对数函数的是 (填序号).
①y=loga(5+x)(a>0 且 a≠1);②y=logj-x;③y=log (-x);
④y=logr\3(x>0 且 x≠1).
2.设函数 f(x)=logax(a>0, 且 a≠1), 若f(x x ...X2022)=6, 则 f(x ) 十
f(x )+f(x3)十 . . +f(x2022)的值是 .
3. 已知函数f(x)=Ig(x+1) 一lg(1—x).
(1)求函数f(x)的定义域;(2)判断函数f(x)的奇偶性.
限时小练
[2. 3.
简解答:[ 1.
目录
>
课堂作业
1.教科书第131页练习第2题;
2.课后练习.
目录
本节内容结束THANKS
目录
M
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
