4.3对数的运算 课件(共39张PPT)-(新教材)人教A版高中数学必修第一册上课用
文档属性
| 名称 | 4.3对数的运算 课件(共39张PPT)-(新教材)人教A版高中数学必修第一册上课用 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-06 11:09:04 | ||
图片预览











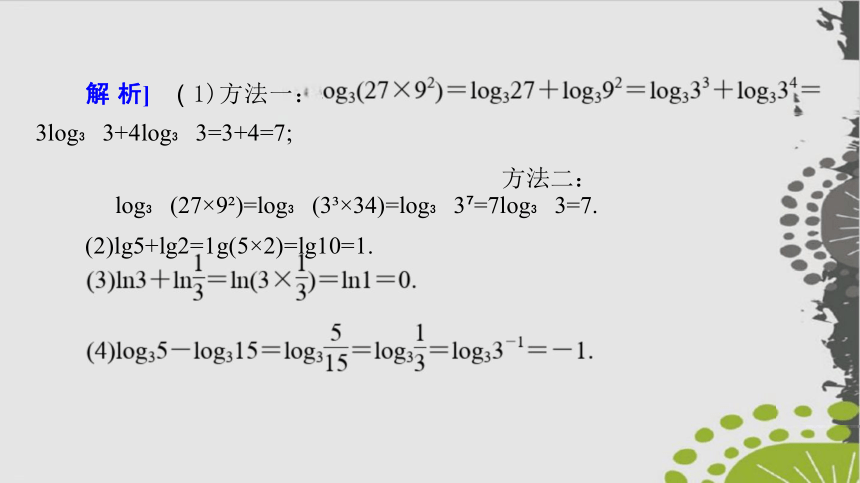
文档简介
(共39张PPT)
第四章
指数函数与对数函数
4.3 对数
4.3.2 对数的运算
目录 CONTENTS
必备知识·探新知
关键能力·攻重难
课堂检测·固双基
素养作业·提技能
必备知识·探新知
条件
a > 0 , 且 a ≠ 1 , M > 0 , N > 0
性质
loga(MN)=log M+log N
og%M=log,M-log,N
logaM"=nlog,M( n∈R)
基础知识
对数的运算性质
知 识 点 1
·思考 1: 在积的对数运算性质中,三项的乘积式log_(MNQ)是否适用 你 能得到一个怎样的结论
·提示: 适用,loga(MNQ =log M+log_N+log_Q, 积的对数运算性质可 以推广到真数是n 个正数的乘积.
思考2:(1)对数的换底公式用常用对数、自然对数表示什么形式
(2)你能用换底公式和对数的运算性质推导出结论
知识点2 换底公式
·若a>0, 且a≠1;b>0;c>0, 且 c≠1, 则有1
吗
提示:(1)
事
垂
基础自测
1 . 若a>0,a≠1,x>0,y>0,x>y,
①logax-logay=loga(x+y);
②logax—logay=loga(x—y);
④loga(xy)=logax-logay.
A.0 B.1
C.2 D.3
》
下列式子中正确的个数是( A )
[解析] 由对数运算法则知,均不正确.故选A.
·2.log 2+log 3 等于( A )
·A.1 B.2
·C.5 D.6
·[解析] log 2+log 3=1og (2×3)=log 6=1.
·3.(2020·天津和平区高一期中测试)计算:log 5·log 2·log 9=_
2
[解析]
4.求下列各式的值:
(1)log (27×9 );(2)lg5+lg2;
3 ;(4)log 5-log 15.
解 析] ( 1)方法一:
3log 3+4log 3=3+4=7;
方法二:log (27×9 )=log (3 ×34)=log 3 =7log 3=7.
(2)lg5+lg2=1g(5×2)=lg10=1.
关键能力·攻重难
例 1 用 logax,logay,logaz 表示:
(1)loga(xy );(2)loga(x√y);(3) 垂
[解析] (1)loga(xy )=logax+logay =logax+2logay.
题型探究
题型一对数的运算性质的应用
》》
·[归纳提升] 对对数式进行计算、化简时, 一要注意准确应用对数的性 质和运算性质.二要注意取值范围对符号的限制.
【对点练习】① 用log x、logay、logaz表示下列各式:
(1)loga(x y ); ② 垂
[解析] (1)loga(x y )=logax +logay =3logax+5logay.
题型二利用对数的运算性质化简、求值
例 2 化简下列各式:
(1)log (2 ×45);
(4)log \8+43+log √ 8-43;
(5)log (1+√2+√3)+log (1+√2-√3).
·[分析] 熟练掌握对数的运算性质并能逆用性质是解题的关键.进行对 数运算,要注意法则的正用和逆用.在化简变形的过程中,要善于观察、 比较和分析,从而选择快捷、有效的运算方案.
[解析](1)log (2 ×4)=log 2 +log 4
=3+5log 4=3+5×2=13.
=1g(2×7)-2(1g7—1g3)+1g7—lg(3 ×2)
=1g2+1g7—2lg7+2lg3+1g7-2lg3—1g2=0.
(4)log √ 8+43+log √ 8-4√3
=log [(√ 8+4√3)(√ 8-4√3)]=log √64-48=log 4=2. (5)log (1+√2+√3)+log (1+√2-√3)
=log [(1+√2) -(3) ]=log (3+2√2-3)
·[归纳提升]利用对数运算性质化简与求值的原则
·(1)正用或逆用公式,对真数进行处理.
·(2)选哪种策略化简,取决于问题的实际情况, 一般本着便于真数化简 的原则进行 .
(2)(2020·江苏、苏州市高一期中测试)(1g5) +lg2×1g50.
[解析](1)原
【对点练习】② 计算下列各式的值:
(1)(2020-湖南衡阳高一期末测试
;
·(2)原式=(1g5) +lg2×1g(5×10) ·=(1g5) +lg2×(1+1g5)
·=(1g5) +1g2+1g2·1g5
·=1g5(1g5+1g2)+lg2
·=1g5+lg2=lg10=1.
题型三换底公式的应用
例3(1)计算
(2)若log 4·log 8·log m=log 2,求 m 的值 .
·[分析] ( 1)对数的底数不同,如何将其化为同底的对数
·(2)等式左边前一个对数的真数是后面对数的底数,利用换底公式很容 易进行约分求解m的值.
;
(2)由题意,
∴m=√3.
[解析] (1)原式
4 即
,∴
[归纳提升] 关于换底公式的用途和本质:
(1)换底公式的主要用途在于将一般对数式化为常用对数或自然对
数,然后查表求值,以此来解决对数求值的问题.
(2)换底公式的本质是化异底为同底,这是解决对数问题的基本方法
(3)在运用换底公式时,若能结合底数间的关系恰当选用一些重要的
结论,如 ;logaa”=n, ;1g2+1g5=1等,将
会达到事半功倍的效果.
【对点练习】③ 计算下列各式的值:
(1)log 9·log 732;
(2)log27;
=log 5- ·log 2- ·log 3-
=—3log 5·(—5log 2)·(—log 3)
=—15.
, ∴x —2x—15=0,∴x=—3 或x=5,
故原方程的解为x=—3 或 x=5.
误区警示
·忽视真数大于零致误
解方程:log (x+1)-log (x+4)=1.
原方程变形为
∴log (x+1)-log \x+4=1,∴
[错解]
例 4
··
手
力
·[错因分析] 解题过程中忽视对数logN 中真数N必须大于0时对数才有意 义.实际上,在解答此类题时,要时刻关注对数本身是否有意义.另外, 在运用对数运算性质或相关公式时也要谨慎,以防出错.
(正解 ∵Jogsx+1)-log(x+4)=1,∴
解得x=5 或 x=—3 (舍去).
∴方程log (x+1)—log (x+4)=1 的解为x=5.
中
·[方法点拨]在将对数方程化为代数方程的过程中,未知数的范围扩大 或缩小就容易产生增根.故解对数方程必须把所求的解代入原方程进行 检验,否则易产生增根,造成解题错误.也可以像本题的求解过程这样 在限制条件下去求解.
学科素养
转化与化归思想的应用与综合分析解决问题的能力
例 5 (1)设3*=4V=36, 的值;
(2)已知log 3=a,3b=7, 求 log 256.
〉>
[分析] (1)欲 的值,已知3*=36,4Y=36, 由此两式怎样得到x,
y, 容易想到对数的定义——故可用等式两端取同底的对数(指对互化)来
解决.
(2)已知条件中有指数式,也有对数式,而待计算式为对数式,因 此
可将指数式3b=7 化为对数式解决.观察所给数字特征、条件式中为2、
3、7,又12=3×2 ,56=7×2 ,故还可以利用换底公式的推论
logab,将条件中的对数式log 3=a 化为指数式解答.
∵3×=36,4Y=36,
∴x=log 36,y=log 36,
由换底公式得:
[解析] (1)由已知分别求出x 和 y,
log 636=1.
事
中
(2)解法一:因为log 3=a, 所以2 =3.又3 =7,故 故56=2 +ab,又12=3×4=2a×4=2a+2,
又3=7,所以og7=.
解法二:因为log 3=a, 所以
·[归纳提升]1.应用换底公式应注意的事项
·(1)注意换底公式的正用、逆用以及变形应用.
·(2)题目中有指数式和对数式时,要注意将指数式与对数式统一成一种
形式,注意转化与化归思想的运用.
·2.对数式的条件求值问题要注意观察所给数字特征,分析找到实现转
化的共同点进行转化.
·3.利用换底公式计算、化简、求值的一般思路:
·思路—:用对数的运算法则及性质进行部分运算→换成同一底数
·思路二: 一次性统一换为常用对数(或自然对数)→化简、通分。求值
课堂检测·固双基
点击进入WORD文档
素养作业提技能
点击进入WORD文档
演示完毕
谢谢欣赏
第四章
指数函数与对数函数
4.3 对数
4.3.2 对数的运算
目录 CONTENTS
必备知识·探新知
关键能力·攻重难
课堂检测·固双基
素养作业·提技能
必备知识·探新知
条件
a > 0 , 且 a ≠ 1 , M > 0 , N > 0
性质
loga(MN)=log M+log N
og%M=log,M-log,N
logaM"=nlog,M( n∈R)
基础知识
对数的运算性质
知 识 点 1
·思考 1: 在积的对数运算性质中,三项的乘积式log_(MNQ)是否适用 你 能得到一个怎样的结论
·提示: 适用,loga(MNQ =log M+log_N+log_Q, 积的对数运算性质可 以推广到真数是n 个正数的乘积.
思考2:(1)对数的换底公式用常用对数、自然对数表示什么形式
(2)你能用换底公式和对数的运算性质推导出结论
知识点2 换底公式
·若a>0, 且a≠1;b>0;c>0, 且 c≠1, 则有1
吗
提示:(1)
事
垂
基础自测
1 . 若a>0,a≠1,x>0,y>0,x>y,
①logax-logay=loga(x+y);
②logax—logay=loga(x—y);
④loga(xy)=logax-logay.
A.0 B.1
C.2 D.3
》
下列式子中正确的个数是( A )
[解析] 由对数运算法则知,均不正确.故选A.
·2.log 2+log 3 等于( A )
·A.1 B.2
·C.5 D.6
·[解析] log 2+log 3=1og (2×3)=log 6=1.
·3.(2020·天津和平区高一期中测试)计算:log 5·log 2·log 9=_
2
[解析]
4.求下列各式的值:
(1)log (27×9 );(2)lg5+lg2;
3 ;(4)log 5-log 15.
解 析] ( 1)方法一:
3log 3+4log 3=3+4=7;
方法二:log (27×9 )=log (3 ×34)=log 3 =7log 3=7.
(2)lg5+lg2=1g(5×2)=lg10=1.
关键能力·攻重难
例 1 用 logax,logay,logaz 表示:
(1)loga(xy );(2)loga(x√y);(3) 垂
[解析] (1)loga(xy )=logax+logay =logax+2logay.
题型探究
题型一对数的运算性质的应用
》》
·[归纳提升] 对对数式进行计算、化简时, 一要注意准确应用对数的性 质和运算性质.二要注意取值范围对符号的限制.
【对点练习】① 用log x、logay、logaz表示下列各式:
(1)loga(x y ); ② 垂
[解析] (1)loga(x y )=logax +logay =3logax+5logay.
题型二利用对数的运算性质化简、求值
例 2 化简下列各式:
(1)log (2 ×45);
(4)log \8+43+log √ 8-43;
(5)log (1+√2+√3)+log (1+√2-√3).
·[分析] 熟练掌握对数的运算性质并能逆用性质是解题的关键.进行对 数运算,要注意法则的正用和逆用.在化简变形的过程中,要善于观察、 比较和分析,从而选择快捷、有效的运算方案.
[解析](1)log (2 ×4)=log 2 +log 4
=3+5log 4=3+5×2=13.
=1g(2×7)-2(1g7—1g3)+1g7—lg(3 ×2)
=1g2+1g7—2lg7+2lg3+1g7-2lg3—1g2=0.
(4)log √ 8+43+log √ 8-4√3
=log [(√ 8+4√3)(√ 8-4√3)]=log √64-48=log 4=2. (5)log (1+√2+√3)+log (1+√2-√3)
=log [(1+√2) -(3) ]=log (3+2√2-3)
·[归纳提升]利用对数运算性质化简与求值的原则
·(1)正用或逆用公式,对真数进行处理.
·(2)选哪种策略化简,取决于问题的实际情况, 一般本着便于真数化简 的原则进行 .
(2)(2020·江苏、苏州市高一期中测试)(1g5) +lg2×1g50.
[解析](1)原
【对点练习】② 计算下列各式的值:
(1)(2020-湖南衡阳高一期末测试
;
·(2)原式=(1g5) +lg2×1g(5×10) ·=(1g5) +lg2×(1+1g5)
·=(1g5) +1g2+1g2·1g5
·=1g5(1g5+1g2)+lg2
·=1g5+lg2=lg10=1.
题型三换底公式的应用
例3(1)计算
(2)若log 4·log 8·log m=log 2,求 m 的值 .
·[分析] ( 1)对数的底数不同,如何将其化为同底的对数
·(2)等式左边前一个对数的真数是后面对数的底数,利用换底公式很容 易进行约分求解m的值.
;
(2)由题意,
∴m=√3.
[解析] (1)原式
4 即
,∴
[归纳提升] 关于换底公式的用途和本质:
(1)换底公式的主要用途在于将一般对数式化为常用对数或自然对
数,然后查表求值,以此来解决对数求值的问题.
(2)换底公式的本质是化异底为同底,这是解决对数问题的基本方法
(3)在运用换底公式时,若能结合底数间的关系恰当选用一些重要的
结论,如 ;logaa”=n, ;1g2+1g5=1等,将
会达到事半功倍的效果.
【对点练习】③ 计算下列各式的值:
(1)log 9·log 732;
(2)log27;
=log 5- ·log 2- ·log 3-
=—3log 5·(—5log 2)·(—log 3)
=—15.
, ∴x —2x—15=0,∴x=—3 或x=5,
故原方程的解为x=—3 或 x=5.
误区警示
·忽视真数大于零致误
解方程:log (x+1)-log (x+4)=1.
原方程变形为
∴log (x+1)-log \x+4=1,∴
[错解]
例 4
··
手
力
·[错因分析] 解题过程中忽视对数logN 中真数N必须大于0时对数才有意 义.实际上,在解答此类题时,要时刻关注对数本身是否有意义.另外, 在运用对数运算性质或相关公式时也要谨慎,以防出错.
(正解 ∵Jogsx+1)-log(x+4)=1,∴
解得x=5 或 x=—3 (舍去).
∴方程log (x+1)—log (x+4)=1 的解为x=5.
中
·[方法点拨]在将对数方程化为代数方程的过程中,未知数的范围扩大 或缩小就容易产生增根.故解对数方程必须把所求的解代入原方程进行 检验,否则易产生增根,造成解题错误.也可以像本题的求解过程这样 在限制条件下去求解.
学科素养
转化与化归思想的应用与综合分析解决问题的能力
例 5 (1)设3*=4V=36, 的值;
(2)已知log 3=a,3b=7, 求 log 256.
〉>
[分析] (1)欲 的值,已知3*=36,4Y=36, 由此两式怎样得到x,
y, 容易想到对数的定义——故可用等式两端取同底的对数(指对互化)来
解决.
(2)已知条件中有指数式,也有对数式,而待计算式为对数式,因 此
可将指数式3b=7 化为对数式解决.观察所给数字特征、条件式中为2、
3、7,又12=3×2 ,56=7×2 ,故还可以利用换底公式的推论
logab,将条件中的对数式log 3=a 化为指数式解答.
∵3×=36,4Y=36,
∴x=log 36,y=log 36,
由换底公式得:
[解析] (1)由已知分别求出x 和 y,
log 636=1.
事
中
(2)解法一:因为log 3=a, 所以2 =3.又3 =7,故 故56=2 +ab,又12=3×4=2a×4=2a+2,
又3=7,所以og7=.
解法二:因为log 3=a, 所以
·[归纳提升]1.应用换底公式应注意的事项
·(1)注意换底公式的正用、逆用以及变形应用.
·(2)题目中有指数式和对数式时,要注意将指数式与对数式统一成一种
形式,注意转化与化归思想的运用.
·2.对数式的条件求值问题要注意观察所给数字特征,分析找到实现转
化的共同点进行转化.
·3.利用换底公式计算、化简、求值的一般思路:
·思路—:用对数的运算法则及性质进行部分运算→换成同一底数
·思路二: 一次性统一换为常用对数(或自然对数)→化简、通分。求值
课堂检测·固双基
点击进入WORD文档
素养作业提技能
点击进入WORD文档
演示完毕
谢谢欣赏
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
