2.3 二次函数与一元二次方程 课件(共32张PPT)-(新教材)人教A版高中数学必修第一册
文档属性
| 名称 | 2.3 二次函数与一元二次方程 课件(共32张PPT)-(新教材)人教A版高中数学必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-06 11:27:52 | ||
图片预览








文档简介
(共32张PPT)
第二章
一元二次函数、方程和不等式
第二章
一元二次函数、方程和不等式
2.3二次函数与一元二次方程、 不等式
设这个矩形的一条边长为x
(12—x) m. 由题意,
得(12—x)x>20,
其中x ∈{x|0整理得
x —12x+20<0 ,
x ∈{x|0求得不等式①的解集,就得到了问题的答案.
m,则另一条边长为
一元二次
不等式
问题园艺师打算在绿地上用栅 栏围一个矩形区域种
植花卉.若栅栏的长度是24 m ,
围成的矩形区域的面积要
大于20 m , 则这个矩形的边 长为多少米
问题引入
一元二次不等式”概念
一般地,我们把只含有一个_未知数,并 且未知数的最高次数是2的不等式,称为一 元二次不等式.一元二次不等式的一般形式是 ax +bx+c>0 或ax +bx+c<0, 其中a,b,c 均 为常数,a ≠0.
提 示:(1)不是, 一元二次不等式一定为整式
不等式.
(2)不可以,若a=0, 就不是二次不等式了.
问题: 一 元二次不等式的求解方法是 什么
(1)不等式x +■>0 是一元二次不等式吗
(2)一元二次不等式的一般形式中“a≠0”可以省
略吗
思考
2.二次函数的零点
一般地,对于二次函数y=ax +bx+c, 我们把使ax +bx+c
= 0 的 _实数x _ 叫做二次函数 y=ax +bx+c 的零点.
温馨提示:(1)二次函数的零点不是点,是二次函数与x 轴 交
点的横坐标.
(2)一元二次方程的根是相应一元二次函数的零点.
概念
先考察一元二次不等式x —12x +20<0
与二次函数y=x — 12x + 20 之间的关系.
分析:当2数图象位于x轴下方,
此 时y<0,
即x —12x+20<0.
所以, 一元二次不等式
x —12x+20<0 的解集是
{x|2探究
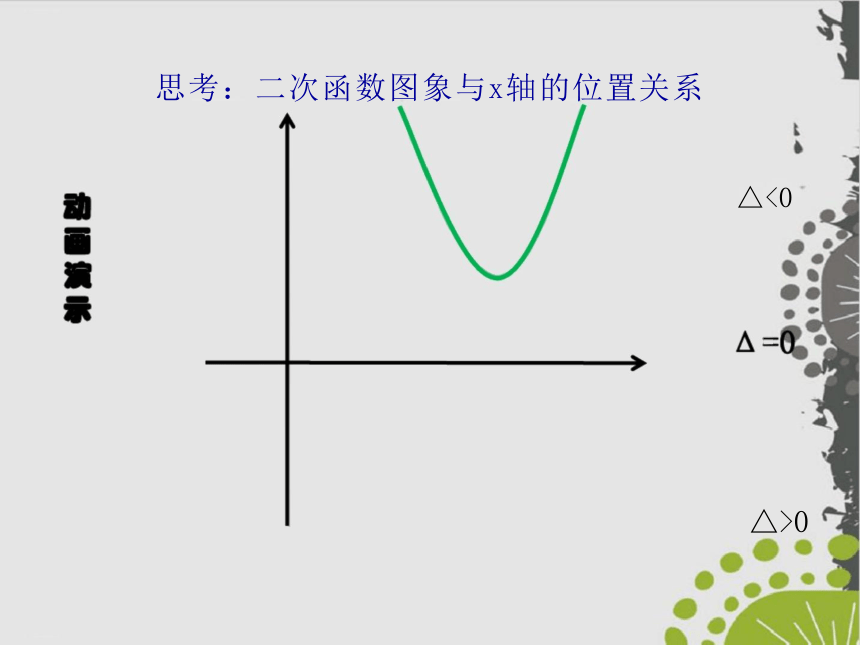
思考:二次函数图象与x轴的位置关系
△<0
△>0
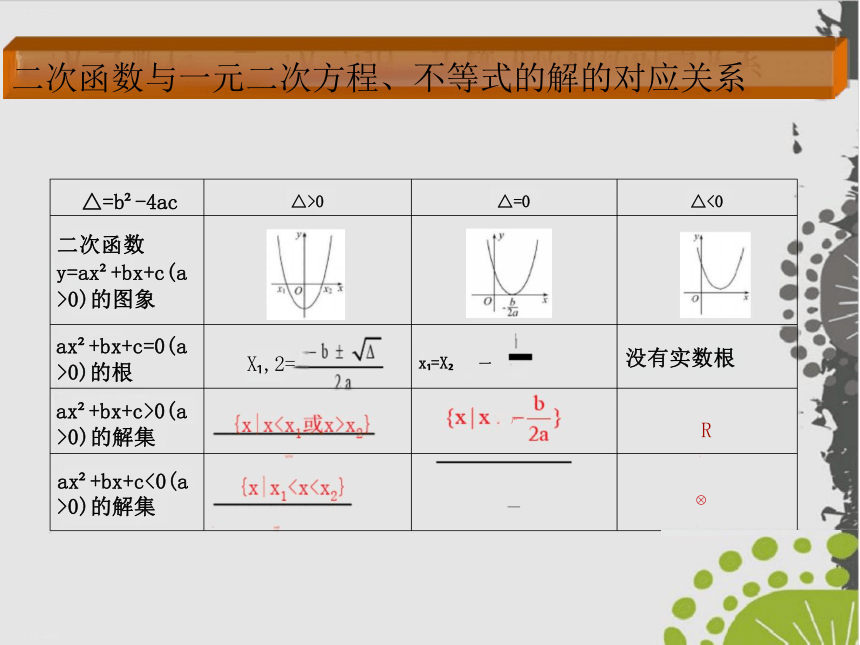
△=b -4ac △>0 △=0
△<0
二次函数 y=ax +bx+c(a >0)的图象
ax +bx+c=0(a >0)的根 X ,2= x =X 一
没有实数根
ax +bx+c>0(a >0)的解集 广
R
ax +bx+c<0(a >0)的解集 —
二次函数与一元二次方程、不等式的解的对应关系
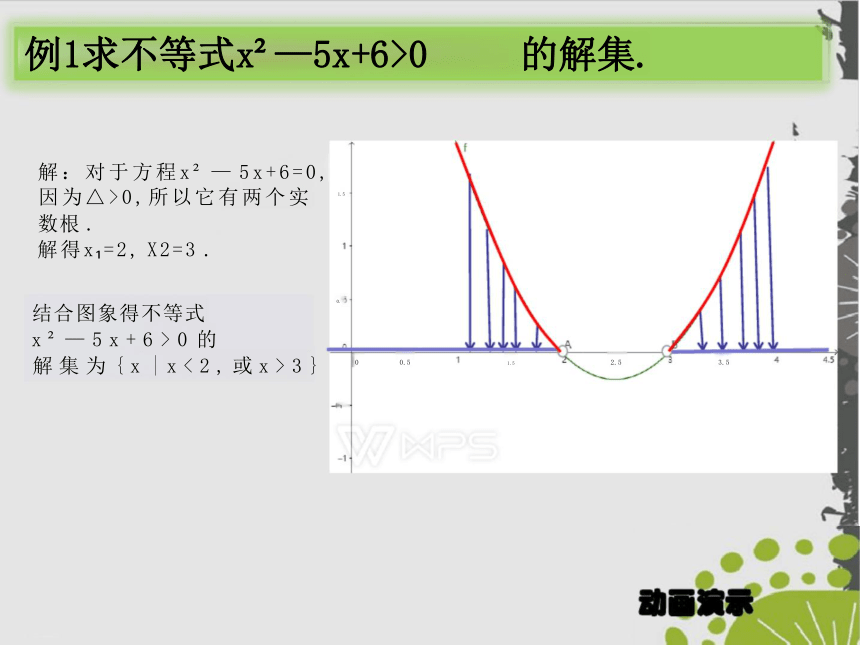
解:对于方程x — 5x+6=0, 因为△>0,所以它有两个实
数根 .
解得x =2, X2=3 .
例1求不等式x —5x+6>0 的解集.
结合图象得不等式
x — 5 x + 6 > 0 的
解 集 为 { x | x < 2 , 或 x > 3 }
0 0.5 1.5 2.5 3.5
1.5
0.
5
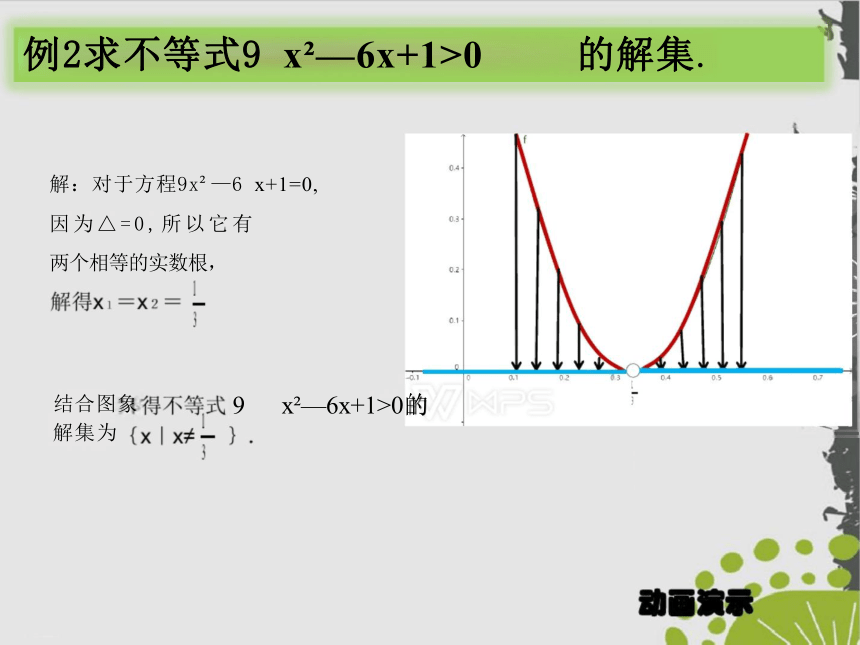
例2求不等式9 x —6x+1>0 的解集.
解:对于方程9x —6 x+1=0,
因为△=0,所以它有
两个相等的实数根,
9 x —6x+1>0的
结合图象
解集为
针对训练
解不等式:
(1)2x —3x—2>0;
(2)一3x +6x—2>0;
(3)4x —4x+1≤0;
(4)x —2x+2>0.
[思路导引] 先求出对应一元二次方程
的解,再结合对应的二次函数的图象写出不
等式的解集.
因为函数是开口向上的抛物线,
所以不等式的解集是x<- 或 x>2.
[解],(1)方程2x —3x—2=0 的解 ,x =2.
方程3x —6x+2=0 的解是
因为函数y=3x -6x+2
的解集是
9 垂
是开口向上的抛物线,所以不等式
的判别式△=36-4×3×2=12>0,所以
(2)不等式可化为3x —6x+2<0.
因为3x -6x+2=0
(4)因为x -2x+2=0 的判别式A<0, 所以方程x -2x+2=0
无解.又因为函数y=x -2x+2 是开口向上的抛物线,所以原不
等式的解集为R.
(3)方程4x -4x+1=0 的解是 函数y=4x -4x+
1是开口向上的抛物线,所以原不等式的解集是
小结:解一元二次不等式的一般步骤
(1)通过对不等式变形,使二次项系数大于零; (2)计算对应方程的判别式;
(3)求出相应的一元二次方程的根,或根据 判别式说明方程没有实根;
(4)根据函数图象与x轴的相关位置写出不 等式的解集.
变式训练
解下列不等式:
(1)一x +7x>6;
(2)(2—x)(x+3)<0;
(3)4(2x —2x+1)>x(4-x).
解 :(1)原不等式可化为x —7x+6<0.
解方程x —7x+6=0 得 ,x =1,x =6.
结合二次函数y=x —7x+6 的图象知,原
不等式的解集为{x|1(2)原不等式可化为(x—2)(x+3)>0.
方程(x—2)(x+3)=0 两根为2和一3.
结合二次函数y=(x—2)(x+3) 的图象知,
原不等式的解集为{x|x<—3或x>2}.
(3)由原不等式得8x —8x+4>4x—x .
∴原不等式等价于9x —12x+4>0.
解方程9x —12x+4=0,
结合二次函数y=9x —12x+4 的图象知,
原不等式的解集为{×4x≠}.
变式训练
3.判断正误(正确的打“ √ ”,错误的打“×”)
(1)mx -5x<0 是一元二次不等式.(× )
(2)若 a>0, 则一元二次不等式ax +1>0 无解 . (× )
(3)若一元二次方程ax +bx+c=0 的两根为x ,x (x一元二次不等式 ax +bx+c<0 的解集为{x|x (4)不等式x -2x+3>0 的解集为R.( √ )
1.(2019·全国卷I) 已知集合M={x|-4( )
A.{x|-4C.{x|-2【解析】选C.由题意得,M={x|-4高频考题
2.已知不等式ax —bx +2<0 的解集为{x|1求a,b 的值.
[分析] 给出了一元二次不等式的解集,则可知a 的
符号和方程ax2—bx+2=0 的两根,由根与系数 的关系可求a,b 的值.
[解析] 方法一:由题设条件知 a>0, 且1,2是方程
的两实根.
方法二:把 x=1,x=2
解
分别代入方程 ax -bx+2=0 中,得
由根与系数的关系,知 解
3.若不等式a x +bx+ c≤0的解集为{x|x≤-3 或x≥4},求 不 等 式
bx +2ax—c—3b≥0 的解集 .
所以不等式 bx +2ax—c-3b≥0 可化为-ax +2ax+15a≥0, 即 x
—2x—15≥0, 解得x≤-3 或 x≥5, 故所求不等式的解集为{x|x≤-3 或 x≥5}.
[解析] 因为不等式 ax +bx+c≤0 以 a<0, 且-3,4是方程ax +bx+c=0
由根与系数的关系可得, 即
的解集为{x|x≤-3 的两根,
或 x≥4}, 所
[解析 ](1)当a=0 时不等式为-x>0, 所以x<0,
(2)当a≠0 时,方程ax -x=0 的两根为0与 ;
①当a>0 时, 所以 x<0;
②当a<0 时, , 所
综上,当a>0, 不等式的解集为 x<0};
当a=0 时,不等式的解集为{x|x<0};
当a<0 时,不等式的解集为
4.解关于x 的不等式ax2—x>0.
垂
5.若O为 ( )
A.{x|3a ≤x≤3a} B.{x|3a≤x≤3a }
C.{x|x≤3a 或x≥3a}D.{x|x≤3a 或x≥3a }
【解析】选A.因为0所以0<3a <3a,而方程x -3(a+a )x+9a =0的两
个根分别为3a和3a ,
所以不等式的解集为{x|3a ≤x≤3a}.
【解析】当a=0时,不等式为-x>0,所
当a≠0 时,方程ax -x=0的两根为0与
当a>0时,■>0,所以x>■ 或x<0;
当a<0时,■<0,所以■综上,当a>0, 不等式的解集
当a=0时,不等式的解集为{x|x<0};
当a<0时,不等式的解集为
6.解关于x的不等式ax -x>0.
以x<0,
;
或x<
7.已知不等式mx2—2x+m —2<0, 若对于
所有的实数x不等式恒成立,求m 的取值范 围 .
[分析] 本题的易错之处在于忽略对二次项系
数为0的讨论,即使不符合题意,也要规范 地解答,这是解题过程的完整性.
[解析] 对于所有实数x 都有不等式mx -2x+m-2<0 恒成立,即函
数y=mx -2x+m-2 的图象全部在x 轴下方 . 当m=0 时 , - 2x-2<0,
显然对任意x 不能恒成立;
当 m≠0 时,由二次函数的图象可知 解得
m<1-√2.
综上可知,m 的取值范围是{mm<1-)2}.
[解析] 若 a=0 时,原不等式为-2x-2≤0 不恒成立,所以a≠0
当a≠0 时,则应
8.若关于x的不等式ax + (a-2)x -2≤0 恒成立, 求实数a的取值范围.
所以实数 a的值为-2.
解得a=-2.
整理
1.一元二次不等式概念
2.零点与方程的根,二次函数与x轴交点
3.二次函数与一元二次方程、不等式的解的 对应关系
4. 一元二次不等式解法
小结
谢谢
观赏
第二章
一元二次函数、方程和不等式
第二章
一元二次函数、方程和不等式
2.3二次函数与一元二次方程、 不等式
设这个矩形的一条边长为x
(12—x) m. 由题意,
得(12—x)x>20,
其中x ∈{x|0
x —12x+20<0 ,
x ∈{x|0
m,则另一条边长为
一元二次
不等式
问题园艺师打算在绿地上用栅 栏围一个矩形区域种
植花卉.若栅栏的长度是24 m ,
围成的矩形区域的面积要
大于20 m , 则这个矩形的边 长为多少米
问题引入
一元二次不等式”概念
一般地,我们把只含有一个_未知数,并 且未知数的最高次数是2的不等式,称为一 元二次不等式.一元二次不等式的一般形式是 ax +bx+c>0 或ax +bx+c<0, 其中a,b,c 均 为常数,a ≠0.
提 示:(1)不是, 一元二次不等式一定为整式
不等式.
(2)不可以,若a=0, 就不是二次不等式了.
问题: 一 元二次不等式的求解方法是 什么
(1)不等式x +■>0 是一元二次不等式吗
(2)一元二次不等式的一般形式中“a≠0”可以省
略吗
思考
2.二次函数的零点
一般地,对于二次函数y=ax +bx+c, 我们把使ax +bx+c
= 0 的 _实数x _ 叫做二次函数 y=ax +bx+c 的零点.
温馨提示:(1)二次函数的零点不是点,是二次函数与x 轴 交
点的横坐标.
(2)一元二次方程的根是相应一元二次函数的零点.
概念
先考察一元二次不等式x —12x +20<0
与二次函数y=x — 12x + 20 之间的关系.
分析:当2
此 时y<0,
即x —12x+20<0.
所以, 一元二次不等式
x —12x+20<0 的解集是
{x|2
思考:二次函数图象与x轴的位置关系
△<0
△>0
△=b -4ac △>0 △=0
△<0
二次函数 y=ax +bx+c(a >0)的图象
ax +bx+c=0(a >0)的根 X ,2= x =X 一
没有实数根
ax +bx+c>0(a >0)的解集 广
R
ax +bx+c<0(a >0)的解集 —
二次函数与一元二次方程、不等式的解的对应关系
解:对于方程x — 5x+6=0, 因为△>0,所以它有两个实
数根 .
解得x =2, X2=3 .
例1求不等式x —5x+6>0 的解集.
结合图象得不等式
x — 5 x + 6 > 0 的
解 集 为 { x | x < 2 , 或 x > 3 }
0 0.5 1.5 2.5 3.5
1.5
0.
5
例2求不等式9 x —6x+1>0 的解集.
解:对于方程9x —6 x+1=0,
因为△=0,所以它有
两个相等的实数根,
9 x —6x+1>0的
结合图象
解集为
针对训练
解不等式:
(1)2x —3x—2>0;
(2)一3x +6x—2>0;
(3)4x —4x+1≤0;
(4)x —2x+2>0.
[思路导引] 先求出对应一元二次方程
的解,再结合对应的二次函数的图象写出不
等式的解集.
因为函数是开口向上的抛物线,
所以不等式的解集是x<- 或 x>2.
[解],(1)方程2x —3x—2=0 的解 ,x =2.
方程3x —6x+2=0 的解是
因为函数y=3x -6x+2
的解集是
9 垂
是开口向上的抛物线,所以不等式
的判别式△=36-4×3×2=12>0,所以
(2)不等式可化为3x —6x+2<0.
因为3x -6x+2=0
(4)因为x -2x+2=0 的判别式A<0, 所以方程x -2x+2=0
无解.又因为函数y=x -2x+2 是开口向上的抛物线,所以原不
等式的解集为R.
(3)方程4x -4x+1=0 的解是 函数y=4x -4x+
1是开口向上的抛物线,所以原不等式的解集是
小结:解一元二次不等式的一般步骤
(1)通过对不等式变形,使二次项系数大于零; (2)计算对应方程的判别式;
(3)求出相应的一元二次方程的根,或根据 判别式说明方程没有实根;
(4)根据函数图象与x轴的相关位置写出不 等式的解集.
变式训练
解下列不等式:
(1)一x +7x>6;
(2)(2—x)(x+3)<0;
(3)4(2x —2x+1)>x(4-x).
解 :(1)原不等式可化为x —7x+6<0.
解方程x —7x+6=0 得 ,x =1,x =6.
结合二次函数y=x —7x+6 的图象知,原
不等式的解集为{x|1
方程(x—2)(x+3)=0 两根为2和一3.
结合二次函数y=(x—2)(x+3) 的图象知,
原不等式的解集为{x|x<—3或x>2}.
(3)由原不等式得8x —8x+4>4x—x .
∴原不等式等价于9x —12x+4>0.
解方程9x —12x+4=0,
结合二次函数y=9x —12x+4 的图象知,
原不等式的解集为{×4x≠}.
变式训练
3.判断正误(正确的打“ √ ”,错误的打“×”)
(1)mx -5x<0 是一元二次不等式.(× )
(2)若 a>0, 则一元二次不等式ax +1>0 无解 . (× )
(3)若一元二次方程ax +bx+c=0 的两根为x ,x (x
1.(2019·全国卷I) 已知集合M={x|-4
A.{x|-4
2.已知不等式ax —bx +2<0 的解集为{x|1
[分析] 给出了一元二次不等式的解集,则可知a 的
符号和方程ax2—bx+2=0 的两根,由根与系数 的关系可求a,b 的值.
[解析] 方法一:由题设条件知 a>0, 且1,2是方程
的两实根.
方法二:把 x=1,x=2
解
分别代入方程 ax -bx+2=0 中,得
由根与系数的关系,知 解
3.若不等式a x +bx+ c≤0的解集为{x|x≤-3 或x≥4},求 不 等 式
bx +2ax—c—3b≥0 的解集 .
所以不等式 bx +2ax—c-3b≥0 可化为-ax +2ax+15a≥0, 即 x
—2x—15≥0, 解得x≤-3 或 x≥5, 故所求不等式的解集为{x|x≤-3 或 x≥5}.
[解析] 因为不等式 ax +bx+c≤0 以 a<0, 且-3,4是方程ax +bx+c=0
由根与系数的关系可得, 即
的解集为{x|x≤-3 的两根,
或 x≥4}, 所
[解析 ](1)当a=0 时不等式为-x>0, 所以x<0,
(2)当a≠0 时,方程ax -x=0 的两根为0与 ;
①当a>0 时, 所以 x<0;
②当a<0 时, , 所
综上,当a>0, 不等式的解集为 x<0};
当a=0 时,不等式的解集为{x|x<0};
当a<0 时,不等式的解集为
4.解关于x 的不等式ax2—x>0.
垂
5.若O
A.{x|3a ≤x≤3a} B.{x|3a≤x≤3a }
C.{x|x≤3a 或x≥3a}D.{x|x≤3a 或x≥3a }
【解析】选A.因为0
个根分别为3a和3a ,
所以不等式的解集为{x|3a ≤x≤3a}.
【解析】当a=0时,不等式为-x>0,所
当a≠0 时,方程ax -x=0的两根为0与
当a>0时,■>0,所以x>■ 或x<0;
当a<0时,■<0,所以■
当a=0时,不等式的解集为{x|x<0};
当a<0时,不等式的解集为
6.解关于x的不等式ax -x>0.
以x<0,
;
或x<
7.已知不等式mx2—2x+m —2<0, 若对于
所有的实数x不等式恒成立,求m 的取值范 围 .
[分析] 本题的易错之处在于忽略对二次项系
数为0的讨论,即使不符合题意,也要规范 地解答,这是解题过程的完整性.
[解析] 对于所有实数x 都有不等式mx -2x+m-2<0 恒成立,即函
数y=mx -2x+m-2 的图象全部在x 轴下方 . 当m=0 时 , - 2x-2<0,
显然对任意x 不能恒成立;
当 m≠0 时,由二次函数的图象可知 解得
m<1-√2.
综上可知,m 的取值范围是{mm<1-)2}.
[解析] 若 a=0 时,原不等式为-2x-2≤0 不恒成立,所以a≠0
当a≠0 时,则应
8.若关于x的不等式ax + (a-2)x -2≤0 恒成立, 求实数a的取值范围.
所以实数 a的值为-2.
解得a=-2.
整理
1.一元二次不等式概念
2.零点与方程的根,二次函数与x轴交点
3.二次函数与一元二次方程、不等式的解的 对应关系
4. 一元二次不等式解法
小结
谢谢
观赏
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
