高中数学必修第一册第1章 集合与常用逻辑用语 复习课件(共96张PPT)
文档属性
| 名称 | 高中数学必修第一册第1章 集合与常用逻辑用语 复习课件(共96张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-06 00:00:00 | ||
图片预览











文档简介
(共96张PPT)
第1章集合与常用逻辑用语 1.1集合的概念
人教A版2019高中数学必修第一册
● 1什么是集合 什么是元素
看下面的例子:
(1)1~10之间的所有偶数; 2,4,6,8,10
(2)卢老师所在初中今年入学的全体高一新生;一 全部新生
(3)所有的正方形; 全部正方形,无数个
(4)到直线M的距离等于定长d的所有点; 点构成了直线
(5)方程x +9x-10=0 的所有解; X =1,X =-10
(6)地球上的七大洲。 → 亚洲、欧洲、北美洲、南美洲、南极洲、非洲、大洋洲
一般地,我们把研究对象统称为元素,如(1)中的几个偶数2,4等;
把由元素组成的总体叫做集合 (简称为塞),如上面左侧的6个集合。
集合中的“对象”所指的范围非常广泛,现实生
活中我看到的、听到的、想到的、触摸到的事物和 抽象的符号等等,都可以看做对象。比如数、点、
图形、多项式、方程、函数、人等等、
集合是一个整体,已暗含“所有”“全部”“全体”
的含义,因此一些对象一旦组成集合,那么这个集合
就是全体,而非个别对象了。
1什么是集合 什么是元素
“总体”
“对象“
2集合当中的元素有哪几种性质
确 定 性 对于一个给定的集合,它的元素必须是确定的。也就是说,对于
一个已知的集合来说,某个元素在不在这个集合里,是确定的,
要么在,要么不在,不能含糊其辞。比如“较小的数”就不能构 成集合,因为组成它的元素是不缺定的。
互异性一个给定的集合当中的元素是互不相同的,即集合中的元素不会
重复出现
无序性集合中的元素排列没有顺序之分,只要某两个集合当中的元素相
同,那么它们就是相等的集合。{1,2,3}和{3,2,1}是 同样的集合
3集合和元素怎么表示 它们之间有什么关系
一般来说:用大写拉丁字母A、B、C...等表示集合
用小写拉丁字母a,b,c.等表示元素
元素与集合的关系:
如果是a是集合A的元素,那么就说a属于集合A, 记作a ∈A;
如果是a不是集合A的元素,那么就说a不属于集合A, 记作atA;
比如,3∈自然数集;44奇数集
●4常用的数集比如自然数集怎么表示 注意写法
【自然数集】全体自然数组成的集合,0,1,2..,记作N, 也叫非负整数集
【正整数集】全体正整数组成的集合,记作N*或N+;
【整数集】 全体整数组成的集合,记作Z;
【有理数集】全体有理数组成的集合,记作Q;
【实数集】 全体实数组成的集合,记作R;
从上面的例子可以看出:我 们可以用自然语言来描述集 合,还可以用什么方法呢
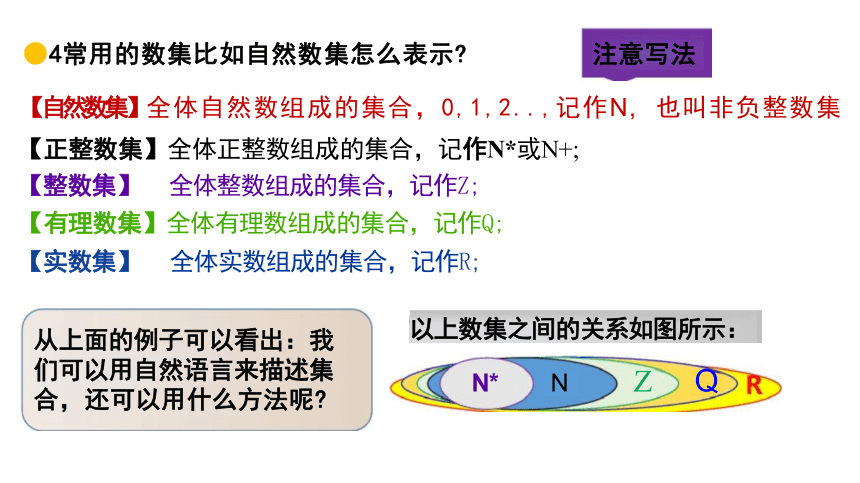
N* N Z Q
以上数集之间的关系如图所示:
【注意】(1)花括号表示的是“所有”“整体”的含义,如实数集可以写成
{实数},但不能写成{实数集}{全体实数}{R}
(2)列举法表示集合时要注意:
①元素之间用逗号隔开;
②一个集合中的元素书写一般不考虑顺序
“地球上的四大洋”组成的集合可以表示为{大西洋,太平洋,北冰洋,印度洋};
“方程x -2x=0 的所有实数根”组成的集合可以表示为{0,2}
像这样,把集合的元素一一列出来,并用花括号{}括起来表示集合的方法叫做列举法。
5集合的3种表示方法之列举
【问题】哪些集合适合用列举法表示呢
(1)含有有限个元素且元素个数较少的集合
(2)元素较多,但是元素的排列呈现一定的规律,在不至于发生误解的情况下,
也可以列出几个元素作代表,其他元素用省略号表示,
如自然数集N可以表示为{0,1,2,...,n...}
(3)当集合所含元素属性特征不易表述时,用列举法比较方便,如 {x,x+y,x ,√x}
5集合的3种表示方法之列举
【有限集】含有有限个元素的集合
【无限集】含有无限个元素的集合
集合的分类
5课堂练习
用列举法表示下列集合
(1)小于8的所有自然数的集合;
(2)方程x +x=0 的所有实数根组成的集合.
【解】(1){0,1,2,3,4,5,6,7}
(2){-1,0}
由于集合具有无序性,所以第(1)题的答案可以有多种呈现方式,
如{1,2,4,5,6,0,7,3}等
注意
6集合的3种表示方法之描述法
一般地,设A是一个集合,我们把集合A 中所有具有共同特征P(x)的元素x
所组成的集合表示为{ x∈A|P(x)}, 这种表示集合的方法称为描述法。
例如,我们可以把奇数集表示为{ x∈Z|x=2k+1(k∈Z)},
偶数集表示为{ x∈Z|x=2k(k∈Z)};
把不等式x-3>0 的解集表示为{ x ∈R|x>3}
注意 有时也用冒号或者分号代替竖线,写成{x∈A:P(x)} 或 { x∈A;P(x)}
问题:用描述法表示集合需要注意什么问题
(1)竖线前面表示的是集合的元素,{ x|y=√x-1},
{y|y=√x-1},{(x,y)|y=√x-1} 分别是三个不同的集合.
(2)竖线后面写清元素满足的条件, 一般是方程或者不等式.
(3)不能出现未说明的字母,
如 {(x|x=2k} 未说明k的取值情况,故集合中的元素不确定.
(4)所有描述内容都要写在花括号里面,
如写法{ (x|x=2k },k∈Z不符合要求,应改为{ (x|x=2k ,k∈Z }
(5)多层描述时,要准确适用“或”“且”等表示元素关系的词语,
如{x|x<-1 或x>2}
6集合的3种表示方法之描述法
6课堂练习
请用描述法表示下列集合:
(1)方程x -4=0 的所有实数根组成的集合A;
(2)由大于10而小于20的所有整数组成的集合B.
解:(1)A={x|x -4=0}
(2)B={x∈Z|10方法 自然语言 列举法
描述法
特点 自然语言是最基 本的语言形式,使用 范围广,但是具有多 义性,有时难于表达。 列举法直观地体 现了元素的个体,但 是有局限性,多适用 于元素个数较少的有 限集。
描述法具有抽象概括、
普遍性的特点,适用于元素 共同特征明显的集合,有些 集合元素没有明显的共同特 征,则不能用描述法。
举例 方程x -1=0的解集 {1}
{x|x -1=0}
7表示集合的三种方法各有什么特点
● 7表示集合的三种方法各有什么特点
明确集合中元素的共同特征
找准代表元素,满足什么条件
列举法表 示的集合
描述法表 示的集合
分析集合中的元素及其特征 逐一列出集合中的元素
形象化
具体化
集合语言 简介、抽象
图形语言
符号语言
文字语言
● 7表示集合的三种方法各有什么特点
图形语言
(形象、
直观)
(通俗、
易懂)
自然语言
,则k =1; 则k =3,不满足题意
, 则k =2; 则k=3, 不满足题意
,则k =9; ,则k =16,不满足题意 ,则k =12; 事 则k=12, 满足题意
【①元素与集合关系的判断】
【解】对于A, 当
,
对于B, 里
对于C, 当x=3,y=4
对于D, 当x=4,y=3
,k∈Z}中的元素的是(D)
C.(3,4) D.(4,3)
时 ,
,
时 ,
时 1
课堂练习
下列选项中是集合
(1)若集合A中含有三个元素a-3,2a-1,a -4, 且-3∈A, 求a
【解】(1)①若a-3=-3, 则 a=0, 此时A={-3,-1,-4}, 满足题意
②若2a-1=-3, 则 a=-1, 此时a -4=2a-1=-3, 不满足题意
③若a -4=-3, 则a=±1,a=1 时 ,A={-2,1,-3}, 满足题意;
a=-1 时,由②知不满足题意;
(2)若24{x|x-a>0}, 求 a的取值范围
(2)∵24{x|x-a>0}, 所以2不满足不等式x-a>0, 即 2 -a≤0,
即α的取值范围为{a|a≥2}
【②已知元素与集合的关系求参数】
课堂练习
【解】由题意 , 易 知a≠0 且a≠1,
则有a+b=0 且b=1!
若b=1, 则 由a+ b=0 得a=-1, 经验证符合题意;
则a=b, 由a+b= 0 得a=b=0, 不符合题意;
综上,a=-1,b=1,a+b=0
【③由集合相等求参数】
含有3个实数的集合既可以表示为 ,又可以表示为{a,a+b,1},
● 课堂练习
则 a+b 的值是多少
●回顾复习
元素与集合:
一般地,我们把研究对象统称为元素;把由元素组成的总体叫做塞合。
集合当中的元素有三种种性质:
确定性、互异性、无序性。
元素与集合的关系:
如果是a是集合A的元素,那么就说a属于集合A, 记作a ∈A;
如果是a不是集合A的元素,那么就说a不属于集合A, 记 作a+A;
常用的数集的表示方法:
自然数集记作N; 正整数集记作N*或N+;
整数集记作Z; 有理数集记作Q; 实数集记作R;
集合的3种表示方法:
自然语言;列举法;描述法
感谢观看
你好
夏天
H E L LO SU M M E R
Ple ase click here Please click here to
anter your content,or copy and
paste your te xt
第1章集合与常用逻辑用语
1.2集合间的基本关系
入效01言学信第一册
1集合A包含集合B是什么意思 什么是子集
观察下面的例子,你能发现集合之间有什么关系吗
(1)A={1,2,3,4},B={1,2,3}
(2)集合A: 高一全体学生,集合B: 高一全体男生
(3)集合M: 所有等腰三角形,集合N: 所有等边三角形
归纳总结:可以发现,在(1)(2)(3)中的两个集合A和B, 集合B中的
每一个元素都是集合A中的元素,我们就说集合A包含集合B, 或者说
集合B包含于集合A。像这样,对于两个集合A,B, 如果集合B中任意 一个元素都是集合A中的元素,就称集合B为集合A的子集,
记作:BCA, 或者A2B, 读作B包含于A,A 包含B
【对子集的理解】
(1)若ASB, 则有任意xEA,xEB
(2)当集合B中存在不属于集合A的元素时,我们就说集合B不是集合A的
子集,记作B 卖A 或ApB, 读作“B不包含于A”或“A不包含B”,
(3)集合中的专业术语只有子集,没有母集或父集
举例说明,若A={1,2,3},B={1,2,3,4},C={1,2,5}, 则有
AS B,A实C,BPC
1集合A包含集合B是什么意思 什么是子集
课堂练习
设集合A={0,1,2}, 集合B={m |m=x+y,x∈A,y∈A},求A与B的关系。
【解】由题意易知m 的情况有如下几种:
m=0+0=0,m=0+1=1,m=0+2=2,m=1+1=2,
m=1+2=3,m=2+2=4,
即m 有0,1,2,3,4—共5种结果,则:
B={0,1,2,3,4}, 所以ASB
【注意】①表示集合的Venn 图的便捷是封闭曲线,它可以是圆、矩形、椭圆、
也可以是其他封闭曲线
② Venn图的优点是形象直观,缺点是公共特征不明显,画图时要注意
区分大小关系。
在数学中,我们经常用平面上的封闭曲线的内部表示集合,这种图叫做Venn 图。
这样,如果AC B,就可以表示如图:
2什么是Venn图
B
A和B两个集合的大小情况如图所示,则A和B的关系是( D )
A.A∈B
B.B∈A
C.AE B
D.BC A
【解】由Venn图易知B是A的子集,即BCA, 选D
课堂练习
一般地,如果集合A的任何一个元素都是集合B的元素,且集合B的任何
一个元素都是集合A 的元素,那么集合A 和集合B相等,记作:
A=B
也就是说,若ACB, 且BSA, 则A=B
【举例说明】
①若集合A:0~10 之间的质数;集合B={2,3,5,7}, 则A=B
②若集合A: 中国的直辖市组成的集合;B={北京,上海,重庆,
天津},则A=B
3两个集合相等是什么意思
3两个集合相等是什么意思
【问题】怎样证明或判定两个集合相等
【答】(1)若ASB, 且BSA, 则A=B, 这就给出了证明两个集合相等的
办法,即要证A=B, 只需证明ASB, 且BSA
(2)判定两个集合相等,可把握两个原则:
①设两个集合A,B 均为有限集,若两个集合中元素个数相同,
且对应元素分别相同,则两个集合相等
②设两个集合A,B 均为无限集,只需看两个集合的代表元素里
及其特征是否相同,若相同,则两个集合相等,即A=B
【解】由题意B中的元素也是1和-1,
因为a ≥0, 所以a =1,
则a=-1或1(舍)
综上,则a=-1
已知集合A和B的关系为A=B, 其中A={1,-1},B={a,a },求a
课堂练习
【对真子集的理解】
①理解真子集概念时,需明确AGB,首先要满足ASB
其次要满足至少有一个元素x∈B, 但x∈A
②注意符号“S”“≠”“E” 的区别,如A={1,2},
B={1,2,3},C={1,2,3}, 则AGB,BSC,C 实A
③没有“假子集”这个概念
4什么是真子集 难道还有假子集
若集合AC B,但存在元素x ∈B, 但x A,即B中有不属于A的元素
存在,那么就称集合A是集合B的真子集,记作:AGB 或 B A
如A={1,2,3},B={1,2,3,4}, 则A B
课堂练习
1.写出集合{1,2,3}的所有子集,并指出哪些是它的真子集
【分析】可把子集分为三类:
【解】子集有a,{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}
其中真子集有a,{1},{2},{3},{1,2},{1,3},{2,3}
【注意】书写子集的时候千万不要漏掉空集
①不含元素的:
③含有两个元素的
②含有一个元素的
④含有三个元素的
课堂练习
2.判断下列各组集合A是否是集合B的子集,说明理由。
(1)A={1,2,3},B={x|x 是8的因数};
(2)A={x|x 是长方形,B={x|x 是两条对角线相等的平行四边形
【解】(1)因为3不是8的因数,所以集合A不是集合B的子集,A≠B
(2)因为长方形的一个定义就是“对角线相等的平行四边形”,
所以A=B, 当然有AC B
一般地,我们把不含任何元素的集合叫做空集,记为a, 并规定:
空集是任何集合的子集,并且:空集是任何非空集合的真子集
我们知道:方程x +4=0
成的集合总没有元素。
5什么是空集
没有实数根,所以方程x +4=0 的实数根组
5什么是空集
比较对象 φ与0 φ与{0}
φ与{φ}
相同点 都表示没有 的意思 都是集合
都是集合
不同点 0是集合 0是实数 0不含任何元素, {0}含有一个元素0
不含任何元素,
{0}是一个集合,含有一个元素φ
关系 0 &φ φ车{0}
0车{0}或O∈{0}
6包含关系{a}S A与属于关系a ∈A 有什么区别
①{a}表示含有一个元素a的集合,{a}≤A表示集合A包含{a},
这是两个集合之间的关系,如{a}≤{a,b,c}
② a∈A, 表示a是集合A 中的一个元素,
这是元素与集合间的关系,如a ∈{a,b,c}
由上述集合间的基本关系,我们可以得到如下结论:
(1)任何一个集合是它本身的子集,即AS A;
(2)对于集合A,B,C, 如果ACB, 且BCC, 那么ACC
即:包含关系具有传递性
1.用适当的数学符号填空。
(1)a ∈ c} (2)0三{(xlx =0}
(3)0_=_ {x∈R|x +1=0}(4){0,1} N
(5){0}_G _ {(x|x =x} (6){2,1} {x|x -3x+2=0}
课堂练习
7如何求某个集合子集的个数
以集合{1,2,3}为例,它的子集可以这么来分析:对于集合{1,2,3}中的每一个元
素1,2,3,在它的子集中都有两种情况:①在子集中②不在子集中,如下表:
元素 在或不在
1
2 X
3 X X
子集 0 {1} {2} {3} {1,2} {1,3} {2,3}
{1,2,3
【规律总结】所以,含有n个元素的集合的子集有2n个 ;真子集有2n-1;
非空子集有2" - 1个;非空真子集有2" - 2个;
1.对于两个集合A,B, 如果集合B中任意一个元素都是集合A中的元素,
就称集合B为集合A的子集,
记 作 :BSA, 或者A 2B,读作B包含于A,A 包含B
2 .子集(1)若ASB, 则有任意xeA,xEB
(2)当集合B中存在不属于集合A的元素时,
我们就说集合B不是集合A的子集,
记作B英A或AP B,读作 “B不包含于A” 或 “A不包含B”
3.两个集合相等:如果集合A的任何一个元素都是集合B的元素,
且集合B的任何一个元素都是集合A的元素,那么集合A和集合B相等,
记 作:A=B也就是说,若AC B,且 BSA, 则A=B
4.真子集:若集合ASB, 但存在元素x ∈B, 但x A,
即B中有不属于A的元素存在,那么就称集合A是集合B的
真子集,记作:AGB 或 B A;
5.空集:我们把不含任何元素的集合叫做空集,记为0,
并规定:空集是任何集合的子集,并且:空集是任何非空集合的
真子集;
6.求某个集合子集的个数方法:含有n个元素的集合的子集有2n个;
真子集有2n-1; 非空子集有2n-1 个;非空真子集有2n-2 个;
课
第1章集合与常用逻辑用语
1.3集合的基本运算
人教A 版2019高中数学必修第一册
观察下面的例子,你能发现集合之间有什么关系吗
(1)A={1,2,3},B={4,5,6},C={1,2,3,4,5,6}
( 2 ) 集 合A={x|x 是奇数},集合B={x|x 是偶数},集合C={x|x 是整数}
可以发现,在(1)(2)中的两个集合A和B和C, 都具有这样一种
关系:集合C是由所有属于集合A和所有属于集合B 的元素组成的。
一般地,由所有属于集合A 或属于集合B的元素组成的集合,
称为集合A 和集合B的并集,记作:AUB, 读 作“A 并B”
1什么是并集 它有什么特点
【注意】集合AUB中的元素个数不一定等于集合A 和集合B中的元
素个数之和,如果集合A和集合B有公共部分的元素,那么这部分元 素只出现一次,如:A={1,2},B={2,3}, 则AUB={1,2,3}, 元素个数
并不是2+2=4个,而是3个
【符号语言表示】 AUB={x|x∈A 或x∈B }
1什么是并集 它有什么特点
【图形语言表示】
1.设集合A={0,1,2,4,5}, 集 合B={2,4,3,5,7},
【解】由题意易知AUB={0,1,2,3,4,5,7}
求AUB。
公共元素在并集里 只出现一次
2.设集合A={x|-1【解】利用数轴可以直观地分析本题两个集合的关
则AUB={x|-1课堂练习
【注意】
(1)并集满足交换律和结合律
①AUB=BUA
②(AUB)UC=AU(BUC)
(2)常用结论:
①AC(AUB),BS(AUB)
②ACB AUB=B
任何集合与其本身的并集都等于自身
任何集合与空集的并集都等于这个集合本身
②A和B有公共元素,
ACAUB,BcAUB
【性质①】AUA=A
【性质②】AUo=A
2并集有什么性质
这三者的关系有如下5种情况:
⑤A=B,则 AUB=A=B
④AEB, 则 AUB=B
③BEA, 则 AUB=A
①A 和B没有公共元素
【拓展】A,B,AUB
观察下面的例子,你能发现集合A,B 和C之间有什么关系吗
(1)A={1,2,3},B={1,3,5},C={1,3}
( 2 ) 集 合A={x|x 是菱形},集合B={x|x 是矩形,集合C={x|x 是正方形
可以发现,在(1)(2)中,集合C中的元素既属于集合A, 又属于集合B, 也
就是说集合C是由集合A 和B的公共元素组成的集合。
一般地,由所有属于A集合且属于B集合的元素组
成的集合,称为集合A与集合B的交集。记作:
ANB , 读 作“A 交B
3什么是交集
【注意】
如果集合A和集合B没有公共元素,
那么也不能说两个集合没有交集,而是它
们的交集是空集,即ANB=0.
例如A={1,2,3},B={(1,1),(2,2),(3,3)},
则ANB=0, 原因是A 是 数 集 ,B是点集,
它们不会有公共元素,所以ANB=Q。
【符号语言表示】
ANB={x|x ∈A 且x ∈B}
【图形语言表示】
3什么是交集
1.飞卢中学开运动会,设A={x|x 是本次参加百米赛跑的同学},
B={x|x 是本次参加跳远的同学},求AUB
【解】由题意AUB={x|x 是本次参加百米赛跑或参加跳远的同学}
2.设平面内直线lA上的点的集合为A, 直线lp上的点的集合为B, 试用集合的
运算来表示直线lA和lg的关系。
【解】平面内的两条直线有三种位置关系:①平行;②相交;③重合
(1)直线lA//l p, 则 A∩B=空集
(2)直线lA和 lp相交于一点P, 则 A∩B={点P}
(3)直线lA和 lp重合,则A∩B= lA=lp
课堂练习
【注意】
(1)交集满足交换律和结合律
①A∩B=BNA
②(A∩B)NC=AN(BNC)
(2)常用结论:
①AN B CA,A∩BcB
②ACB A∩B=A
任何集合与其本身的交集都等于自身
任何集合与空集的交集都等于空集
这三者的关系有如下5种情况:
③BEA, 则 ANB=B
④ASB, 则 A∩B=A
【性质①】ANA=A
【性质②】ANo=0
【拓展】A,B,A∩B
①A和B没有公共元素, 则A∩B=空
②A 和B有公共元素, AN BCA ,A∩BC B
4交集有哪些运算性质
④A=B,则 ANB=A=B
1.设A={3,4,5,6},B={3,5,7,8}, 求AUB,A∩B
【解】AUB={3,4,5,6,7,8},A∩B={3,5}
2.设A={x|x -4x-5=0},B={x|x =1}, 求AUB,A∩B。
【解】由题意易得A={-1,5},B={-1,1}, 则AUB={-1,1,5},A∩B={-1}
3.设A={x|x 是等腰三角形},B={x|x 是直角三角形,求AUB,A∩B。
【解】由题意得AUB={x|x 是等腰三角形或直角三角形};
ANB={x|x 是等腰直角三角形}
课堂练习
【全集】一般地,如果一个集合中含有我们所研究的问题中涉及的所有元素,
那么就称这个集合为全集。也就是我们讨论的范围。 一般记作“U”
【补集】对于一个集合A, 由全集U中不属于集合A的所有元素组成的集合,称
为集合A 相对于全集U的补集,简称为集合A的补集,记作“CyA”
【举例说明】假设全集为整数集Z,A={x|x 为奇数},则:
CyA={x|x 为偶数}
5什么是补集
【注意】
(1)全集不是固定不变的,研究不同的问题,
涉及到的全集一般不一样。
(2)补集是相对于全集而言的,如果没有定义
全集,那么就不存在补集的说法;并且,补 集的元素不能超出全集的范围。
(3)补集既是集合间的一种关系,也是集合间
的一种运算,在给定全集U的情况下,求集合 A的补集的前提是A为全集U的子集。
【符号语言表示】
CuA={x|x∈U 且xfA}
【图形语言表示】
5什么是补集
U
2.设全集U={x|x 是三角形},A={x|x 是锐角三角形},B={x|x
求ANB,Cu(AU B)
【解】根据三角形的分类可知: A∩B=0
AUB={x|x 是锐角三角形或钝角三角形},
则Cu(AUB)={x|x 是直角三角形}
1.设U={x|x 是小于9的正整数},A={1,2,3},B={4,5,6},求CuA,CuB
【解】由题意U={1,2,3,4,5,6,7,8},
则CuA={4,5,6,7,8},CuB={1,2,3,7,8}
是钝角三角形},
课堂练习
集合A和A的补集,它们的并集是全集
集合A和A的补集,它们的交集是空集
集合A的补集的补集,是集合A自身
【性质①】AUCuA=U
【性质②】An CuA=0
【性质③】Cu(CuA)=A
【性质④】CuU=0,Cu×=U 全集的补集是空集,空集的补集是全集
AN CuB A∩B BNCuA Cu(AU B)
6补集有哪些性质
【Venn图】
B
CuA
A∩B
A B B
【拓展】德 ·摩根定律(反演律):设U 为 全 集 ,A,B 为其子集,则有:
(1)Cu(ANB)=(CuA)U(CuB) “交集之补,等于补集之并”如图①
(2)Cu(A U B)=(CyA)n(CuB) “并集之补,等于补集之交”如图②
Cu(A∩B) 二 (CuA)U(CuB) Cu(AU B) 二 (CuA)n(CuB)
我 是 图① 我是图②
6补集有哪些性质
B
AU B
B
CuB
B
CuB
CuA
B
B
1.已知U={12,3,4,5,6,7},A={2,4,5},B={1,3,5,7}, 求An(CuB),(CuA)n(CuB)
【解】 CuB={2,4,6}, 则An(CuB)={2,4,5}n{2,4,6}={2,4}
CuA={1,3,6,7},则(CuA)n(CuB)={1,3,6,7}n{2,4,6}={6}
2.设U={x|x是平行四边形或梯形},A={x|x是平行四边形},B={x|x 是菱形},
C={x|x 是矩形},求B nC,CuB,CuA
【解】BN C={x|x是正方形},
CuB={x|x 是邻边不相等的平行四边形或梯形}, CuA={x|x 是梯形}
课 堂 练 习
1.并集:由所有属于集合A 或属于集合B的元素组成的集合,称为集合A 和集合B的并集。 记作:AUB ,读 作 “A并B“
符号语言:AUB={x|x∈A 或x ∈B}
2.并集的性质:【性质①】AUA=A;【 性质②】AU0=A
3.交集:由所有属于A集合且属于B集合的元素组成的集合,称为集合A与集合B的交集。
记作:A∩B,读 作“A交B”
符号语言:AUB={x|x∈A 且x ∈B}
4.交集的性质:【性质①】ANA=A;【 性质②】ANo=0
回顾复习
5.补集对于一个集合A, 由全集U中不属于集合A的所有元素组成的集合,称为集合A
相对于全集U的补集,简称为集合A的补集,记作“CyA”
符号语言: CuA={x|x∈U 且xA}
【性质②】An CuA=0 集合A和A 的补集,它们的交集是空集
【性质③】Cu(CuA)=A 集合A的补集的补集,是集合A自身
【性质④】CuU=0,Cu×=U 全集的补集是空集,空集的补集是全集
6.补集的性质:
【性质①】AUCuA=U
集合A和A的补集,它们的并集是全集
回顾复习
第1章集合与常用逻辑用语
1.4充分条件与必要条件
A2 B
人Aeo
观察下面的例子,你能发现集合之间有什么关系吗
(1)A={1,2},B={1,2,3}
(2)集合A={x|x 是奇数},集合B={x|x 是整数}
可以发现,在(1)(2)中,如果元素属于集合A, 那么一定也属于B。
一般地,“若p, 则q”为真命题,是指由p可以推导出q, 记 作 :p→q,
并且说p是q的充分条件;q 是p的必要条件。反之,如果由p不能推导出q, 那
么就说p不是q的充分条件,q不是p的必要条件,记作:p≠q
1什么是充分条件 什么是必要条件
q
p → q 我是你的必要条件
【对充分与必要条件的理解】
①p是q的充分条件说明p→q, 而q是p的
必要条件也说明了p>q, 所 以 :“p 是q的
充分条件”和“q 是p的必要条件”表述
的是同一个逻辑关系。而“p是q的充分条
件”只能说明p=q, 与 q能否推导出p没有 任何关系。
②注意右侧等价的表述方式:
【1】 p=q
【2】 p是q的充分条件
【3】 q的充分条件是p
【4】 q 是p的必要条件
【5】 p的必要条件是q
1什么是充分条件 什么是必要条件
课堂练习
1.用符号“→”与“书”填空。
①x >1_ 书 x >1.② a,b 都是偶数 →_a +b 是偶数.
【解】① x >1→x >1 或x<-1, 所以填“书”;
②偶数+偶数=偶数,所以填“→”
2.下列说法是否正确
① “x>1” 是 “x>2” 的充分条件;
② “x+y>2” 是 “x>1,y>1” 的必要条件
【解】① 当x=1.5 时,左边不能推导出右边,则这种说法错误;
② 因为x>1,y>1, 所 以x+y>1+1=2,
右边可以推导出左边,正确。
一般地,如果p可以推导出q, 并且q也可以推导出p, 即p>q, 且 有
q→ p, 则相当于p q 或者q p, 称 作q是p的充分必要条件,q 也是p的 充分必要条件,简称充要条件。
【注意】充要条件是相互的,同时存在的,p=q 即p和q互为充要条件.
【逆命题】将命题“若p, 则q” 中的条件和结论互换,就得到一个新的命题:
“若q, 则 p”, 这个就是原命题的逆命题。
2什么是充要条件
【充要条件】
p与q的关系
结论
p=q,且q≠p
p是q的充分不必要条件
p≠q,且q=p
p是q的必要不充分条件
p=q,且q→p
p是q的充要条件
p≠q,且q≠p
p是q的既不充分也不必要条件
【注意】p 是q的充要条件也可以说成:
① p和q是 等 价 的 ②p成立当且仅当q成 立 ③q成立当且仅当p成立
2什么是充要条件
1.指出下列各组中p是q的什么条件。
①p: 两个三角形相似,q: 两个三角形全等;
【解】相似不一定全等,p≠q; 全等一定相似,q>p,
所以p是q的必要要不充分条件
② p: 一个四边形是矩形,q: 四边形的对角线相等;
【解】矩形的对角线相等, p→q ;对角线相等的四边形不一定是矩形,
也可能是等腰梯形等,q≠p, 所以p是q的充分不必要条件
课堂练习
2.设集合A={1,a ,-2}, 集合B={2,4}, 则 “a=2” 是 “ANB={4}” 的 ( A ) 条 件
A.充分不必要 B. 必要不充分 C.充要 D.既不充分也不必要
【解】若a=2, 则A={1,4,-2},A∩B={4}, 满足充分条件要求;
若A∩B={4}, 则 a =4, 解得a=2 或a=-2, 不满足必要条件要求;
所以 “a=2” 是 “A∩B={4}” 的充分不必要条件,选A
课堂练习
(1)分清命题的条件和结论
(2)找推式,判断p→q 和q→p 的真假
(3)根据条件和推式得出结论
将命题转化成为另一个与之等价的且便于判断真假的命题
对于选择题,可以取一些特殊值或者特殊情况,用来说明
结论或者推导不成立,但不可用于证明题。
3怎么判断充要条件 有哪些方法
【2】等价法
【3】赋值法
【1】定义法:
3怎么判断充要条件 有哪些方法
【3】集合法:列出集合A={x|p(x)}和集合B={x|q(x)},利用集合的
包含关系来判断,如图:
ACB且BtA
p 是q的既不充分也不必要条件
BCA
p 是q 的必要不充分条件
AEB
p 是q 的充分不必要条件
A=B
p 是q的充要条件
1.指出下列各组中p是q的什么条件。
①p:(x-2)(x-3)=0;q:x-2=0
【解】化 简 ,p:x∈{2,3};q:x∈{2}, 则q代表的集合Q是p代表的集合P
的真子集,即Q 车P, 所 以p是q的必要不充分条件
②p:四边形的对角线相等;q: 四边形是矩形
【解】对角线相等的四边形不一定是矩形,p≠q;
矩形的对角线相等,q>p, 所 以p 是q的必要不充分条件
课堂练习
(1)充分条件与必要条件都有传递性,具体如下:
①若p=q,q>s 则有p=s, 即 p是s的充分条件;
②若s=q,q>p 则有s=p, 即 p是s的必要条件;
③若p→q,q→s, 则有p s, 即 p是s的充要条件;
(2)给定命题“若p, 则q”, 对于p是q的什么条件的证明:
①证明充分性,则需证明p=q;
②证明必要性,则需证明q>p;
4充分条件与必要条件的传递性
【问题】已 知p,q 都是r 的充分条件,s是r 的必要条件,q是s的必要条件,那么:
①s是q的什么条件 ②r是q的什么条件 ③p是q的什么条件
【解】利用图示,表示出p,q,s,r 之间的关系如下:
①因为q>r,r=s, 所以q=s; 又 有s=q, 所以s是q的充要条件
②因为r=s,s=q, 所以r=q; 又 有q=r, 所以r 是q的充要条件
③因为p=r,r→s,s>q, 所以p>q; 又有q≠p, 所 以p是q的充分不必要条件
4充分条件与必要条件的传递性
1.下列各组题中,哪些p是q 的充要条件 为什么
①p: 三角形为等腰三角形,q:三角形存在两角相等;
【解】因为p和q代表的都是等腰三角形,所以p=q,
即p q,p 是q的充要条件;
② p:圆O 内两条弦相等,q:圆O 内两条弦所对的圆周角相等;
【解】圆0内两条弦相等,则它们所对的圆周角相等或互补,因此p≠q,
所以p不是q的充要条件;
课堂练习
5本节考试常考什么 【充分条件,必要条件,充要条件的判断】 【题1·定义法】判断下列各题中p是q的什么条件
①p:x-3=0,q:(x-2)(x-3)=0;
【解】因为x-3=0→ (x-2)(x-3), 但(x-2)(x-3)≠x-3=0,
所以p是q的充分不必要条件;
②p:两个三角形相似,q:两个三角形全等;
【解】因为相似不一定全等,但全等一定相似,即p≠q,q>p,
所以p是q的必要不充分条件;
③p:x=y,q:x+t=y+t;
【解】因为由p推导到q和由q 推导到p 都是等式的基本性质,所以p→q且q>p,
所以p是q的充要条件.
【题2·集合法】判断下列各图中A是B的什么条件
【解】因为BSA, 所 以A是B的充分不必要条件
5本节考试常考什么
【解】因为A≠B且BCA, 所以A是B的既不充分也不必要条件
【解】因为A=B, 所 以A是B的充要条件
【充分条件,必要条件,充要条件的判断】
③
②
【题3·传递法】已知p是r的充分不必要条件,q是r的充分条件,s是r的必要条件,
q是s的必要条件,则p是q的什么条件
【解】由题意有p>r,r≠p,q=r,r→s,s=q, 所以p>r→S→q,
而 ,q=r≠p, 即p是q的充分不必要条件,
【注意】本题也可以用图形法,列出p,q,r,s 的关系图:
5本节考试常考什么
在图中路径p=r→s→q可以走通,但q=r≠p 走不通,同样可以得出结论.
【充分条件,必要条件,充要条件的判断】
p
牛
Y q
S
回顾复习
1.充分条件、必要条件:“若p, 则q”为真命题,是指由p可以推导出q, 记 作 :p>q, 并且说p是q的充分条件;q是p的必要条件。
2.充要条件:如果p可以推导出q, 并且q也可以推导出p, 即p=q, 且有q→p, 则相当于p=q 或者q p, 称作q是p的充分必要条件,q也是p的充分必要条件,简称充要条件。
3.判断充要条件的方法:(1)定义法;(2)等价法;(3)赋值法;(4)集合法
4.给定命题“若p, 则q”, 对于p是q的什么条件的证明:
①证明充分性,则需证明p=q;②证明必要性,则需证明q=p;
下课
第1章集合与常用逻辑用语
1.5 全称量词与存在量词
人教A 版2019高中数学必修第一册
1全称量词与全称量词命题
下列语句是命题吗 比较(1)和(3),(2)和(4),你有什么发现
(1)x>3 (2)2x+1 是整数
(3)对所有的x∈R,x>3; (4) 对任意一个x∈Z,2x+1 是整数
可以发现,语句(1)(2)中含有变量x, 由于不知道x的值,所以无法判断它们的
真假,所以(1)(2)不是命题;而(3)(4)在(1)(2)的基础上对变量x进行了限 定,用了“任意一个”条件,所以(3)(4)可以判断真假,它们是命题。
短语“所有的““任意一个”在逻辑中一般叫做全称量词,用符号“v”
表示,含有全称量词的命题,叫做全称量词命题;例如命题“对任意的x ∈Z, 2x+1 是奇数““所有的正方形都是矩形”都是全称量词命题
1全称量词与全称量词命题
通常,将含有变量x的语句用p(x),q(x),r(x)等等来表示,变量x的范围
用M 表示。那么,全称量词命题“对M 中任意一个x,p(x) 成立”可用符号简
记为
Vx∈M,p(x)
常见的全称量词有“一切”“每一个”“任给““所有的“
“全部的”“只要是”“任意的”“凡是”等等
Vx∈N,
x>0
我能判断真假,
而且是假命题!
我不能判断真 假,不是命题
x>0
【2】一个全称量词命题可以表示包含多个变量,如“Vx∈R,y∈R ,x +y ≥0”
【3】全称量词命题中一般含有全称量词,但是有些全称量词命题
中的全称量词是省略的,理解时需要把它补充出来,例如“平行四 边形的对角线互相平分”应理解为“所有的平行四边形对角线都互 相平分”
1全称量词与全称量词命题
【1】从集合的观点来看,全称量词命题是陈述某个集合中的所有元
素都具有某种相同的性质。因此,全称量词表示的数量可以是无限 的,也可以是有限的。这取决于所描述的这个集合中的元素的个
数。
课堂练习
请用不同表述方法表示全称量词命题“Vx∈M,p(x)”
【解】表述①:对所有的x∈M,p(x)成立
表述②:对一切x∈M,p(x)成立
表述③:对每一个x∈M,p(x)成立
表述④:任选一个x∈M,p(x)成立
表述⑤:凡是x∈M,p(x)成立
要判断全称量词命题“Vx∈M,p(x)” 是真命题,需要对集合中每
一个元素x, 证 明p(x) 成立;如果在集合中找到一个元素x , 使 得p(x) 不 成立,那么这个全称量词命题就是假命题.
它为真,我
要好好说明 下;它为假, 我一个反例 就说明了!
★要判断全称量词命题是假命
题,只需找一个反例即可.
★要判断全称量词命题是真命
题,需要从左往右地推导;
2全称量词命题怎么判断真假
全称 量词 命 题
也就是说,
2全称量词命题怎么判断真假
【例题】判断下列全称量词命题的真假
(1)所有的素数都是奇数;
【解】2是素数,但是2不是奇数,所以命题为假.
(2)Vx∈ R,|x|+1≥1;
【解】因为Vx∈R,|x|≥0, 所以|x|+1≥1, 命题为真
(3)对任意一个无理数x,x 也是无理数.
【解】因为 √2是无理数,但是(√2) = 2是有理数,
所以命题为假.
温肆提示
素数,即质数,
一个正整数,除 了1和自身之外 没有其他整数的 因数,则成为素
数(质数) .
课堂练习
判断下列全称量词命题的真假:
①每个四边形的对角线都互相垂直
【解】右图所示的四边形对角线就不垂直,
所以命题为假.
②Vxe{y|y是无理数},x 是无理数
【解】右x=33 是无理数,但x =( √3) =3
是有理数,所以命题为假;
③任何实数都有算术平方根
【解】-4是实数,但是-4没有算术平方根,
所以命题为假;
温留提示
非负数才有平方
根和算术平方根;负 数没有平方根,更没 有算术平方根.
3存在量词与存在量词命题
下列语句是命题吗 比较(1)和(3),(2)和(4),它们之间有什么关系
(1)2x+1=3; (2)x 能被2和3整除
(3)存在 一 个x∈R, 使2x+1 =3;(4) 至少有一个x ∈Z,x 能被2和3整除
可以发现, (1)(2)不是命题,而(3)在(1)的基础上,用短语
“存在一个”对变量的x取值进行了限定; (4)在(2)的基础上,用短语 “至少有一个”对变量的取值进行了限定;所以(3)(4)可以判断真假, 因此它们是命题。
短语“存在一个”“至少有一个”在逻辑中一般叫做存在量词,用符号
“3”表示,含有存在量词的命题,叫做存在量词命题;例如命题“有的平行 四边形是菱形”“存在不是素数的奇数”等都是存在量词命题.
3存在量词与存在量词命题
通常,将含有变量x的语句用p(x),q(x),r(x) 等等来表示,变量x的范围
用M表示。那么,存在量词命题 “M中存在一个x,p(x) 成立”可用符号简
记为
3x∈M,p(x)
常见的存在量词有“存在”“某一个”“任给”“对部分“
“对某个““对某些““有一个““有的”等 等
3x∈N,
x>0
我能判断真假, 而且是真命题!
我不能判断真 假,不是命题
x>0
【3】含有存在量词“存在”“有一个”等的命题,或虽没有写出存 在量词,但其意义具备“存在”“有一个”等特征的命题都是存在 性命题.
【4】一个存在量词命题中可以包含多个变量,如“3a,b使(a +b) =(a-b) ”.
【1】从集合的观点来看,存在量词命题是陈述某个集合中的某些 (个)元素所具有的某种性质。
【2】含有存在量词的命题,不管包含的程度有多大,都是存在量词 命题.如“存在无数个x∈R, 使x-1>0” 中,无数个也不能代表每 一个.
3存在量词与存在量词命题
课堂练习
请用不同表述方法表示存在量词命题“3x∈M,p(x)”
【解】表述①:至少有一个x ∈M,p(x)成立
表述②:存在x ∈M,p(x) 成立
表述③:对有些x ∈M,p(x)成立
表述④:对某个x ∈M,p(x) 成立
表述⑤;有一个x ∈M,p(x) 成立
要判断全称量词命题“3x∈M,p(x)” 是真命题,只需在集合M 中 找
到一个元素x, 证 明p(x)成立即可;如果在集合M 中找不到任何元素,使 得p(x) 成立,那么这个存在量词命题就是假命题.
★要判断存在量词命题是真命
题,只需要找出一个x满足条
件 ;
★要判断全称量词命题是假命
题,需要推导证明.
它为真,我 只要找出一 个例子就可 以;它为假, 我得证明!
4存在量词命题怎么判断真假
全称 量词 命 题
也就是说,
4存在量词命题怎么判断真假
【例题】判断下列存在量词命题的真假 (1)存在一个四边形的内角和是180°;
【解】所有四边形内角和为360°,所以命题为假.
(2)至少有一个整数n; 使得n -n 是奇数;
【解】因为n -n= n(n-1), 它是两个连续整数
的乘积,结果是偶数,所以命题为假;
(3)存在一个无理数x,x 是有理数.
【解】因为√2是无理数,( √2) =2是有理数,
所以命题为真.
无理数的平方,有
可能是有理数,如 √2,
( √2) =2;也有可能
是无理数,如
√3- √2,它的平方是3
- √2,还是无理数.
温留提示
②平面内存在一对有交点的平行线
【解】右平面内两条直线平行则没有交点,所以命题为假.
③有些平行四边形是菱形
【解】菱形是特殊的平行四边形,所以命题为真
温留提示
平面内两条直线的
位置关系有三种:
①平行,没有交点;
②相交,有一个交点;
③重合,有无数个交点.
课堂练习
判断下列存在量词命题的真假:
①有一个实数x, 使得x +2x-3=0
【解】右x=1 时 ,x +2x-3=1+2-3=0,
所以命题为真.
【例题】已知方程(a +5)x +2(a+1)x+a-5=0
(1)若3a ∈R, 使方程有一个实根,求a的取值范围.
【解】当a+5=0 即a=-5 时,方程化为-8x-10=0, 方程有 ,满足题意; 当a+5≠0 即a≠5 时,方程为一元二次方程,方程有解等价于△≥0,
即△=[2(a+1)] -4(a+5)(a-5)≥0, 解得a≥-13
综上,a≥-13
( 2 ) 若Va∈M, 方程无解,求集合M
【解】由(1)知方程无解等价于△<0,即△=[2(a+1)] -4(a+5)(a-5)<0,
解得a<-13, 所 以M={a|a<-13}
5本节考试常考什么
【含有一个量词的命题求参数间题】
1.全称量词命题“对M 中任意一个x,p(x) 成立”可用符号简记为:Vx∈M,p(x)
2.判断全称量词命题的真假:
★要判断全称量词命题是真命题,需要从左往右地推导;
★要判断全称量词命题是假命题,只需找一个反例即可.
3.存在量词命题“M 中存在一个x,p(x) 成立”可用符号简记为:3 x∈M,p(x)
4.判断存在量词命题的真假:
★要判断存在量词命题是真命题,只需要找出一个x满足条件; ★要判断全称量词命题是假命题,需要推导证明.
回顾复习
下 课
第1章集合与常用逻辑用语 1.1集合的概念
人教A版2019高中数学必修第一册
● 1什么是集合 什么是元素
看下面的例子:
(1)1~10之间的所有偶数; 2,4,6,8,10
(2)卢老师所在初中今年入学的全体高一新生;一 全部新生
(3)所有的正方形; 全部正方形,无数个
(4)到直线M的距离等于定长d的所有点; 点构成了直线
(5)方程x +9x-10=0 的所有解; X =1,X =-10
(6)地球上的七大洲。 → 亚洲、欧洲、北美洲、南美洲、南极洲、非洲、大洋洲
一般地,我们把研究对象统称为元素,如(1)中的几个偶数2,4等;
把由元素组成的总体叫做集合 (简称为塞),如上面左侧的6个集合。
集合中的“对象”所指的范围非常广泛,现实生
活中我看到的、听到的、想到的、触摸到的事物和 抽象的符号等等,都可以看做对象。比如数、点、
图形、多项式、方程、函数、人等等、
集合是一个整体,已暗含“所有”“全部”“全体”
的含义,因此一些对象一旦组成集合,那么这个集合
就是全体,而非个别对象了。
1什么是集合 什么是元素
“总体”
“对象“
2集合当中的元素有哪几种性质
确 定 性 对于一个给定的集合,它的元素必须是确定的。也就是说,对于
一个已知的集合来说,某个元素在不在这个集合里,是确定的,
要么在,要么不在,不能含糊其辞。比如“较小的数”就不能构 成集合,因为组成它的元素是不缺定的。
互异性一个给定的集合当中的元素是互不相同的,即集合中的元素不会
重复出现
无序性集合中的元素排列没有顺序之分,只要某两个集合当中的元素相
同,那么它们就是相等的集合。{1,2,3}和{3,2,1}是 同样的集合
3集合和元素怎么表示 它们之间有什么关系
一般来说:用大写拉丁字母A、B、C...等表示集合
用小写拉丁字母a,b,c.等表示元素
元素与集合的关系:
如果是a是集合A的元素,那么就说a属于集合A, 记作a ∈A;
如果是a不是集合A的元素,那么就说a不属于集合A, 记作atA;
比如,3∈自然数集;44奇数集
●4常用的数集比如自然数集怎么表示 注意写法
【自然数集】全体自然数组成的集合,0,1,2..,记作N, 也叫非负整数集
【正整数集】全体正整数组成的集合,记作N*或N+;
【整数集】 全体整数组成的集合,记作Z;
【有理数集】全体有理数组成的集合,记作Q;
【实数集】 全体实数组成的集合,记作R;
从上面的例子可以看出:我 们可以用自然语言来描述集 合,还可以用什么方法呢
N* N Z Q
以上数集之间的关系如图所示:
【注意】(1)花括号表示的是“所有”“整体”的含义,如实数集可以写成
{实数},但不能写成{实数集}{全体实数}{R}
(2)列举法表示集合时要注意:
①元素之间用逗号隔开;
②一个集合中的元素书写一般不考虑顺序
“地球上的四大洋”组成的集合可以表示为{大西洋,太平洋,北冰洋,印度洋};
“方程x -2x=0 的所有实数根”组成的集合可以表示为{0,2}
像这样,把集合的元素一一列出来,并用花括号{}括起来表示集合的方法叫做列举法。
5集合的3种表示方法之列举
【问题】哪些集合适合用列举法表示呢
(1)含有有限个元素且元素个数较少的集合
(2)元素较多,但是元素的排列呈现一定的规律,在不至于发生误解的情况下,
也可以列出几个元素作代表,其他元素用省略号表示,
如自然数集N可以表示为{0,1,2,...,n...}
(3)当集合所含元素属性特征不易表述时,用列举法比较方便,如 {x,x+y,x ,√x}
5集合的3种表示方法之列举
【有限集】含有有限个元素的集合
【无限集】含有无限个元素的集合
集合的分类
5课堂练习
用列举法表示下列集合
(1)小于8的所有自然数的集合;
(2)方程x +x=0 的所有实数根组成的集合.
【解】(1){0,1,2,3,4,5,6,7}
(2){-1,0}
由于集合具有无序性,所以第(1)题的答案可以有多种呈现方式,
如{1,2,4,5,6,0,7,3}等
注意
6集合的3种表示方法之描述法
一般地,设A是一个集合,我们把集合A 中所有具有共同特征P(x)的元素x
所组成的集合表示为{ x∈A|P(x)}, 这种表示集合的方法称为描述法。
例如,我们可以把奇数集表示为{ x∈Z|x=2k+1(k∈Z)},
偶数集表示为{ x∈Z|x=2k(k∈Z)};
把不等式x-3>0 的解集表示为{ x ∈R|x>3}
注意 有时也用冒号或者分号代替竖线,写成{x∈A:P(x)} 或 { x∈A;P(x)}
问题:用描述法表示集合需要注意什么问题
(1)竖线前面表示的是集合的元素,{ x|y=√x-1},
{y|y=√x-1},{(x,y)|y=√x-1} 分别是三个不同的集合.
(2)竖线后面写清元素满足的条件, 一般是方程或者不等式.
(3)不能出现未说明的字母,
如 {(x|x=2k} 未说明k的取值情况,故集合中的元素不确定.
(4)所有描述内容都要写在花括号里面,
如写法{ (x|x=2k },k∈Z不符合要求,应改为{ (x|x=2k ,k∈Z }
(5)多层描述时,要准确适用“或”“且”等表示元素关系的词语,
如{x|x<-1 或x>2}
6集合的3种表示方法之描述法
6课堂练习
请用描述法表示下列集合:
(1)方程x -4=0 的所有实数根组成的集合A;
(2)由大于10而小于20的所有整数组成的集合B.
解:(1)A={x|x -4=0}
(2)B={x∈Z|10
描述法
特点 自然语言是最基 本的语言形式,使用 范围广,但是具有多 义性,有时难于表达。 列举法直观地体 现了元素的个体,但 是有局限性,多适用 于元素个数较少的有 限集。
描述法具有抽象概括、
普遍性的特点,适用于元素 共同特征明显的集合,有些 集合元素没有明显的共同特 征,则不能用描述法。
举例 方程x -1=0的解集 {1}
{x|x -1=0}
7表示集合的三种方法各有什么特点
● 7表示集合的三种方法各有什么特点
明确集合中元素的共同特征
找准代表元素,满足什么条件
列举法表 示的集合
描述法表 示的集合
分析集合中的元素及其特征 逐一列出集合中的元素
形象化
具体化
集合语言 简介、抽象
图形语言
符号语言
文字语言
● 7表示集合的三种方法各有什么特点
图形语言
(形象、
直观)
(通俗、
易懂)
自然语言
,则k =1; 则k =3,不满足题意
, 则k =2; 则k=3, 不满足题意
,则k =9; ,则k =16,不满足题意 ,则k =12; 事 则k=12, 满足题意
【①元素与集合关系的判断】
【解】对于A, 当
,
对于B, 里
对于C, 当x=3,y=4
对于D, 当x=4,y=3
,k∈Z}中的元素的是(D)
C.(3,4) D.(4,3)
时 ,
,
时 ,
时 1
课堂练习
下列选项中是集合
(1)若集合A中含有三个元素a-3,2a-1,a -4, 且-3∈A, 求a
【解】(1)①若a-3=-3, 则 a=0, 此时A={-3,-1,-4}, 满足题意
②若2a-1=-3, 则 a=-1, 此时a -4=2a-1=-3, 不满足题意
③若a -4=-3, 则a=±1,a=1 时 ,A={-2,1,-3}, 满足题意;
a=-1 时,由②知不满足题意;
(2)若24{x|x-a>0}, 求 a的取值范围
(2)∵24{x|x-a>0}, 所以2不满足不等式x-a>0, 即 2 -a≤0,
即α的取值范围为{a|a≥2}
【②已知元素与集合的关系求参数】
课堂练习
【解】由题意 , 易 知a≠0 且a≠1,
则有a+b=0 且b=1!
若b=1, 则 由a+ b=0 得a=-1, 经验证符合题意;
则a=b, 由a+b= 0 得a=b=0, 不符合题意;
综上,a=-1,b=1,a+b=0
【③由集合相等求参数】
含有3个实数的集合既可以表示为 ,又可以表示为{a,a+b,1},
● 课堂练习
则 a+b 的值是多少
●回顾复习
元素与集合:
一般地,我们把研究对象统称为元素;把由元素组成的总体叫做塞合。
集合当中的元素有三种种性质:
确定性、互异性、无序性。
元素与集合的关系:
如果是a是集合A的元素,那么就说a属于集合A, 记作a ∈A;
如果是a不是集合A的元素,那么就说a不属于集合A, 记 作a+A;
常用的数集的表示方法:
自然数集记作N; 正整数集记作N*或N+;
整数集记作Z; 有理数集记作Q; 实数集记作R;
集合的3种表示方法:
自然语言;列举法;描述法
感谢观看
你好
夏天
H E L LO SU M M E R
Ple ase click here Please click here to
anter your content,or copy and
paste your te xt
第1章集合与常用逻辑用语
1.2集合间的基本关系
入效01言学信第一册
1集合A包含集合B是什么意思 什么是子集
观察下面的例子,你能发现集合之间有什么关系吗
(1)A={1,2,3,4},B={1,2,3}
(2)集合A: 高一全体学生,集合B: 高一全体男生
(3)集合M: 所有等腰三角形,集合N: 所有等边三角形
归纳总结:可以发现,在(1)(2)(3)中的两个集合A和B, 集合B中的
每一个元素都是集合A中的元素,我们就说集合A包含集合B, 或者说
集合B包含于集合A。像这样,对于两个集合A,B, 如果集合B中任意 一个元素都是集合A中的元素,就称集合B为集合A的子集,
记作:BCA, 或者A2B, 读作B包含于A,A 包含B
【对子集的理解】
(1)若ASB, 则有任意xEA,xEB
(2)当集合B中存在不属于集合A的元素时,我们就说集合B不是集合A的
子集,记作B 卖A 或ApB, 读作“B不包含于A”或“A不包含B”,
(3)集合中的专业术语只有子集,没有母集或父集
举例说明,若A={1,2,3},B={1,2,3,4},C={1,2,5}, 则有
AS B,A实C,BPC
1集合A包含集合B是什么意思 什么是子集
课堂练习
设集合A={0,1,2}, 集合B={m |m=x+y,x∈A,y∈A},求A与B的关系。
【解】由题意易知m 的情况有如下几种:
m=0+0=0,m=0+1=1,m=0+2=2,m=1+1=2,
m=1+2=3,m=2+2=4,
即m 有0,1,2,3,4—共5种结果,则:
B={0,1,2,3,4}, 所以ASB
【注意】①表示集合的Venn 图的便捷是封闭曲线,它可以是圆、矩形、椭圆、
也可以是其他封闭曲线
② Venn图的优点是形象直观,缺点是公共特征不明显,画图时要注意
区分大小关系。
在数学中,我们经常用平面上的封闭曲线的内部表示集合,这种图叫做Venn 图。
这样,如果AC B,就可以表示如图:
2什么是Venn图
B
A和B两个集合的大小情况如图所示,则A和B的关系是( D )
A.A∈B
B.B∈A
C.AE B
D.BC A
【解】由Venn图易知B是A的子集,即BCA, 选D
课堂练习
一般地,如果集合A的任何一个元素都是集合B的元素,且集合B的任何
一个元素都是集合A 的元素,那么集合A 和集合B相等,记作:
A=B
也就是说,若ACB, 且BSA, 则A=B
【举例说明】
①若集合A:0~10 之间的质数;集合B={2,3,5,7}, 则A=B
②若集合A: 中国的直辖市组成的集合;B={北京,上海,重庆,
天津},则A=B
3两个集合相等是什么意思
3两个集合相等是什么意思
【问题】怎样证明或判定两个集合相等
【答】(1)若ASB, 且BSA, 则A=B, 这就给出了证明两个集合相等的
办法,即要证A=B, 只需证明ASB, 且BSA
(2)判定两个集合相等,可把握两个原则:
①设两个集合A,B 均为有限集,若两个集合中元素个数相同,
且对应元素分别相同,则两个集合相等
②设两个集合A,B 均为无限集,只需看两个集合的代表元素里
及其特征是否相同,若相同,则两个集合相等,即A=B
【解】由题意B中的元素也是1和-1,
因为a ≥0, 所以a =1,
则a=-1或1(舍)
综上,则a=-1
已知集合A和B的关系为A=B, 其中A={1,-1},B={a,a },求a
课堂练习
【对真子集的理解】
①理解真子集概念时,需明确AGB,首先要满足ASB
其次要满足至少有一个元素x∈B, 但x∈A
②注意符号“S”“≠”“E” 的区别,如A={1,2},
B={1,2,3},C={1,2,3}, 则AGB,BSC,C 实A
③没有“假子集”这个概念
4什么是真子集 难道还有假子集
若集合AC B,但存在元素x ∈B, 但x A,即B中有不属于A的元素
存在,那么就称集合A是集合B的真子集,记作:AGB 或 B A
如A={1,2,3},B={1,2,3,4}, 则A B
课堂练习
1.写出集合{1,2,3}的所有子集,并指出哪些是它的真子集
【分析】可把子集分为三类:
【解】子集有a,{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}
其中真子集有a,{1},{2},{3},{1,2},{1,3},{2,3}
【注意】书写子集的时候千万不要漏掉空集
①不含元素的:
③含有两个元素的
②含有一个元素的
④含有三个元素的
课堂练习
2.判断下列各组集合A是否是集合B的子集,说明理由。
(1)A={1,2,3},B={x|x 是8的因数};
(2)A={x|x 是长方形,B={x|x 是两条对角线相等的平行四边形
【解】(1)因为3不是8的因数,所以集合A不是集合B的子集,A≠B
(2)因为长方形的一个定义就是“对角线相等的平行四边形”,
所以A=B, 当然有AC B
一般地,我们把不含任何元素的集合叫做空集,记为a, 并规定:
空集是任何集合的子集,并且:空集是任何非空集合的真子集
我们知道:方程x +4=0
成的集合总没有元素。
5什么是空集
没有实数根,所以方程x +4=0 的实数根组
5什么是空集
比较对象 φ与0 φ与{0}
φ与{φ}
相同点 都表示没有 的意思 都是集合
都是集合
不同点 0是集合 0是实数 0不含任何元素, {0}含有一个元素0
不含任何元素,
{0}是一个集合,含有一个元素φ
关系 0 &φ φ车{0}
0车{0}或O∈{0}
6包含关系{a}S A与属于关系a ∈A 有什么区别
①{a}表示含有一个元素a的集合,{a}≤A表示集合A包含{a},
这是两个集合之间的关系,如{a}≤{a,b,c}
② a∈A, 表示a是集合A 中的一个元素,
这是元素与集合间的关系,如a ∈{a,b,c}
由上述集合间的基本关系,我们可以得到如下结论:
(1)任何一个集合是它本身的子集,即AS A;
(2)对于集合A,B,C, 如果ACB, 且BCC, 那么ACC
即:包含关系具有传递性
1.用适当的数学符号填空。
(1)a ∈ c} (2)0三{(xlx =0}
(3)0_=_ {x∈R|x +1=0}(4){0,1} N
(5){0}_G _ {(x|x =x} (6){2,1} {x|x -3x+2=0}
课堂练习
7如何求某个集合子集的个数
以集合{1,2,3}为例,它的子集可以这么来分析:对于集合{1,2,3}中的每一个元
素1,2,3,在它的子集中都有两种情况:①在子集中②不在子集中,如下表:
元素 在或不在
1
2 X
3 X X
子集 0 {1} {2} {3} {1,2} {1,3} {2,3}
{1,2,3
【规律总结】所以,含有n个元素的集合的子集有2n个 ;真子集有2n-1;
非空子集有2" - 1个;非空真子集有2" - 2个;
1.对于两个集合A,B, 如果集合B中任意一个元素都是集合A中的元素,
就称集合B为集合A的子集,
记 作 :BSA, 或者A 2B,读作B包含于A,A 包含B
2 .子集(1)若ASB, 则有任意xeA,xEB
(2)当集合B中存在不属于集合A的元素时,
我们就说集合B不是集合A的子集,
记作B英A或AP B,读作 “B不包含于A” 或 “A不包含B”
3.两个集合相等:如果集合A的任何一个元素都是集合B的元素,
且集合B的任何一个元素都是集合A的元素,那么集合A和集合B相等,
记 作:A=B也就是说,若AC B,且 BSA, 则A=B
4.真子集:若集合ASB, 但存在元素x ∈B, 但x A,
即B中有不属于A的元素存在,那么就称集合A是集合B的
真子集,记作:AGB 或 B A;
5.空集:我们把不含任何元素的集合叫做空集,记为0,
并规定:空集是任何集合的子集,并且:空集是任何非空集合的
真子集;
6.求某个集合子集的个数方法:含有n个元素的集合的子集有2n个;
真子集有2n-1; 非空子集有2n-1 个;非空真子集有2n-2 个;
课
第1章集合与常用逻辑用语
1.3集合的基本运算
人教A 版2019高中数学必修第一册
观察下面的例子,你能发现集合之间有什么关系吗
(1)A={1,2,3},B={4,5,6},C={1,2,3,4,5,6}
( 2 ) 集 合A={x|x 是奇数},集合B={x|x 是偶数},集合C={x|x 是整数}
可以发现,在(1)(2)中的两个集合A和B和C, 都具有这样一种
关系:集合C是由所有属于集合A和所有属于集合B 的元素组成的。
一般地,由所有属于集合A 或属于集合B的元素组成的集合,
称为集合A 和集合B的并集,记作:AUB, 读 作“A 并B”
1什么是并集 它有什么特点
【注意】集合AUB中的元素个数不一定等于集合A 和集合B中的元
素个数之和,如果集合A和集合B有公共部分的元素,那么这部分元 素只出现一次,如:A={1,2},B={2,3}, 则AUB={1,2,3}, 元素个数
并不是2+2=4个,而是3个
【符号语言表示】 AUB={x|x∈A 或x∈B }
1什么是并集 它有什么特点
【图形语言表示】
1.设集合A={0,1,2,4,5}, 集 合B={2,4,3,5,7},
【解】由题意易知AUB={0,1,2,3,4,5,7}
求AUB。
公共元素在并集里 只出现一次
2.设集合A={x|-1
则AUB={x|-1
【注意】
(1)并集满足交换律和结合律
①AUB=BUA
②(AUB)UC=AU(BUC)
(2)常用结论:
①AC(AUB),BS(AUB)
②ACB AUB=B
任何集合与其本身的并集都等于自身
任何集合与空集的并集都等于这个集合本身
②A和B有公共元素,
ACAUB,BcAUB
【性质①】AUA=A
【性质②】AUo=A
2并集有什么性质
这三者的关系有如下5种情况:
⑤A=B,则 AUB=A=B
④AEB, 则 AUB=B
③BEA, 则 AUB=A
①A 和B没有公共元素
【拓展】A,B,AUB
观察下面的例子,你能发现集合A,B 和C之间有什么关系吗
(1)A={1,2,3},B={1,3,5},C={1,3}
( 2 ) 集 合A={x|x 是菱形},集合B={x|x 是矩形,集合C={x|x 是正方形
可以发现,在(1)(2)中,集合C中的元素既属于集合A, 又属于集合B, 也
就是说集合C是由集合A 和B的公共元素组成的集合。
一般地,由所有属于A集合且属于B集合的元素组
成的集合,称为集合A与集合B的交集。记作:
ANB , 读 作“A 交B
3什么是交集
【注意】
如果集合A和集合B没有公共元素,
那么也不能说两个集合没有交集,而是它
们的交集是空集,即ANB=0.
例如A={1,2,3},B={(1,1),(2,2),(3,3)},
则ANB=0, 原因是A 是 数 集 ,B是点集,
它们不会有公共元素,所以ANB=Q。
【符号语言表示】
ANB={x|x ∈A 且x ∈B}
【图形语言表示】
3什么是交集
1.飞卢中学开运动会,设A={x|x 是本次参加百米赛跑的同学},
B={x|x 是本次参加跳远的同学},求AUB
【解】由题意AUB={x|x 是本次参加百米赛跑或参加跳远的同学}
2.设平面内直线lA上的点的集合为A, 直线lp上的点的集合为B, 试用集合的
运算来表示直线lA和lg的关系。
【解】平面内的两条直线有三种位置关系:①平行;②相交;③重合
(1)直线lA//l p, 则 A∩B=空集
(2)直线lA和 lp相交于一点P, 则 A∩B={点P}
(3)直线lA和 lp重合,则A∩B= lA=lp
课堂练习
【注意】
(1)交集满足交换律和结合律
①A∩B=BNA
②(A∩B)NC=AN(BNC)
(2)常用结论:
①AN B CA,A∩BcB
②ACB A∩B=A
任何集合与其本身的交集都等于自身
任何集合与空集的交集都等于空集
这三者的关系有如下5种情况:
③BEA, 则 ANB=B
④ASB, 则 A∩B=A
【性质①】ANA=A
【性质②】ANo=0
【拓展】A,B,A∩B
①A和B没有公共元素, 则A∩B=空
②A 和B有公共元素, AN BCA ,A∩BC B
4交集有哪些运算性质
④A=B,则 ANB=A=B
1.设A={3,4,5,6},B={3,5,7,8}, 求AUB,A∩B
【解】AUB={3,4,5,6,7,8},A∩B={3,5}
2.设A={x|x -4x-5=0},B={x|x =1}, 求AUB,A∩B。
【解】由题意易得A={-1,5},B={-1,1}, 则AUB={-1,1,5},A∩B={-1}
3.设A={x|x 是等腰三角形},B={x|x 是直角三角形,求AUB,A∩B。
【解】由题意得AUB={x|x 是等腰三角形或直角三角形};
ANB={x|x 是等腰直角三角形}
课堂练习
【全集】一般地,如果一个集合中含有我们所研究的问题中涉及的所有元素,
那么就称这个集合为全集。也就是我们讨论的范围。 一般记作“U”
【补集】对于一个集合A, 由全集U中不属于集合A的所有元素组成的集合,称
为集合A 相对于全集U的补集,简称为集合A的补集,记作“CyA”
【举例说明】假设全集为整数集Z,A={x|x 为奇数},则:
CyA={x|x 为偶数}
5什么是补集
【注意】
(1)全集不是固定不变的,研究不同的问题,
涉及到的全集一般不一样。
(2)补集是相对于全集而言的,如果没有定义
全集,那么就不存在补集的说法;并且,补 集的元素不能超出全集的范围。
(3)补集既是集合间的一种关系,也是集合间
的一种运算,在给定全集U的情况下,求集合 A的补集的前提是A为全集U的子集。
【符号语言表示】
CuA={x|x∈U 且xfA}
【图形语言表示】
5什么是补集
U
2.设全集U={x|x 是三角形},A={x|x 是锐角三角形},B={x|x
求ANB,Cu(AU B)
【解】根据三角形的分类可知: A∩B=0
AUB={x|x 是锐角三角形或钝角三角形},
则Cu(AUB)={x|x 是直角三角形}
1.设U={x|x 是小于9的正整数},A={1,2,3},B={4,5,6},求CuA,CuB
【解】由题意U={1,2,3,4,5,6,7,8},
则CuA={4,5,6,7,8},CuB={1,2,3,7,8}
是钝角三角形},
课堂练习
集合A和A的补集,它们的并集是全集
集合A和A的补集,它们的交集是空集
集合A的补集的补集,是集合A自身
【性质①】AUCuA=U
【性质②】An CuA=0
【性质③】Cu(CuA)=A
【性质④】CuU=0,Cu×=U 全集的补集是空集,空集的补集是全集
AN CuB A∩B BNCuA Cu(AU B)
6补集有哪些性质
【Venn图】
B
CuA
A∩B
A B B
【拓展】德 ·摩根定律(反演律):设U 为 全 集 ,A,B 为其子集,则有:
(1)Cu(ANB)=(CuA)U(CuB) “交集之补,等于补集之并”如图①
(2)Cu(A U B)=(CyA)n(CuB) “并集之补,等于补集之交”如图②
Cu(A∩B) 二 (CuA)U(CuB) Cu(AU B) 二 (CuA)n(CuB)
我 是 图① 我是图②
6补集有哪些性质
B
AU B
B
CuB
B
CuB
CuA
B
B
1.已知U={12,3,4,5,6,7},A={2,4,5},B={1,3,5,7}, 求An(CuB),(CuA)n(CuB)
【解】 CuB={2,4,6}, 则An(CuB)={2,4,5}n{2,4,6}={2,4}
CuA={1,3,6,7},则(CuA)n(CuB)={1,3,6,7}n{2,4,6}={6}
2.设U={x|x是平行四边形或梯形},A={x|x是平行四边形},B={x|x 是菱形},
C={x|x 是矩形},求B nC,CuB,CuA
【解】BN C={x|x是正方形},
CuB={x|x 是邻边不相等的平行四边形或梯形}, CuA={x|x 是梯形}
课 堂 练 习
1.并集:由所有属于集合A 或属于集合B的元素组成的集合,称为集合A 和集合B的并集。 记作:AUB ,读 作 “A并B“
符号语言:AUB={x|x∈A 或x ∈B}
2.并集的性质:【性质①】AUA=A;【 性质②】AU0=A
3.交集:由所有属于A集合且属于B集合的元素组成的集合,称为集合A与集合B的交集。
记作:A∩B,读 作“A交B”
符号语言:AUB={x|x∈A 且x ∈B}
4.交集的性质:【性质①】ANA=A;【 性质②】ANo=0
回顾复习
5.补集对于一个集合A, 由全集U中不属于集合A的所有元素组成的集合,称为集合A
相对于全集U的补集,简称为集合A的补集,记作“CyA”
符号语言: CuA={x|x∈U 且xA}
【性质②】An CuA=0 集合A和A 的补集,它们的交集是空集
【性质③】Cu(CuA)=A 集合A的补集的补集,是集合A自身
【性质④】CuU=0,Cu×=U 全集的补集是空集,空集的补集是全集
6.补集的性质:
【性质①】AUCuA=U
集合A和A的补集,它们的并集是全集
回顾复习
第1章集合与常用逻辑用语
1.4充分条件与必要条件
A2 B
人Aeo
观察下面的例子,你能发现集合之间有什么关系吗
(1)A={1,2},B={1,2,3}
(2)集合A={x|x 是奇数},集合B={x|x 是整数}
可以发现,在(1)(2)中,如果元素属于集合A, 那么一定也属于B。
一般地,“若p, 则q”为真命题,是指由p可以推导出q, 记 作 :p→q,
并且说p是q的充分条件;q 是p的必要条件。反之,如果由p不能推导出q, 那
么就说p不是q的充分条件,q不是p的必要条件,记作:p≠q
1什么是充分条件 什么是必要条件
q
p → q 我是你的必要条件
【对充分与必要条件的理解】
①p是q的充分条件说明p→q, 而q是p的
必要条件也说明了p>q, 所 以 :“p 是q的
充分条件”和“q 是p的必要条件”表述
的是同一个逻辑关系。而“p是q的充分条
件”只能说明p=q, 与 q能否推导出p没有 任何关系。
②注意右侧等价的表述方式:
【1】 p=q
【2】 p是q的充分条件
【3】 q的充分条件是p
【4】 q 是p的必要条件
【5】 p的必要条件是q
1什么是充分条件 什么是必要条件
课堂练习
1.用符号“→”与“书”填空。
①x >1_ 书 x >1.② a,b 都是偶数 →_a +b 是偶数.
【解】① x >1→x >1 或x<-1, 所以填“书”;
②偶数+偶数=偶数,所以填“→”
2.下列说法是否正确
① “x>1” 是 “x>2” 的充分条件;
② “x+y>2” 是 “x>1,y>1” 的必要条件
【解】① 当x=1.5 时,左边不能推导出右边,则这种说法错误;
② 因为x>1,y>1, 所 以x+y>1+1=2,
右边可以推导出左边,正确。
一般地,如果p可以推导出q, 并且q也可以推导出p, 即p>q, 且 有
q→ p, 则相当于p q 或者q p, 称 作q是p的充分必要条件,q 也是p的 充分必要条件,简称充要条件。
【注意】充要条件是相互的,同时存在的,p=q 即p和q互为充要条件.
【逆命题】将命题“若p, 则q” 中的条件和结论互换,就得到一个新的命题:
“若q, 则 p”, 这个就是原命题的逆命题。
2什么是充要条件
【充要条件】
p与q的关系
结论
p=q,且q≠p
p是q的充分不必要条件
p≠q,且q=p
p是q的必要不充分条件
p=q,且q→p
p是q的充要条件
p≠q,且q≠p
p是q的既不充分也不必要条件
【注意】p 是q的充要条件也可以说成:
① p和q是 等 价 的 ②p成立当且仅当q成 立 ③q成立当且仅当p成立
2什么是充要条件
1.指出下列各组中p是q的什么条件。
①p: 两个三角形相似,q: 两个三角形全等;
【解】相似不一定全等,p≠q; 全等一定相似,q>p,
所以p是q的必要要不充分条件
② p: 一个四边形是矩形,q: 四边形的对角线相等;
【解】矩形的对角线相等, p→q ;对角线相等的四边形不一定是矩形,
也可能是等腰梯形等,q≠p, 所以p是q的充分不必要条件
课堂练习
2.设集合A={1,a ,-2}, 集合B={2,4}, 则 “a=2” 是 “ANB={4}” 的 ( A ) 条 件
A.充分不必要 B. 必要不充分 C.充要 D.既不充分也不必要
【解】若a=2, 则A={1,4,-2},A∩B={4}, 满足充分条件要求;
若A∩B={4}, 则 a =4, 解得a=2 或a=-2, 不满足必要条件要求;
所以 “a=2” 是 “A∩B={4}” 的充分不必要条件,选A
课堂练习
(1)分清命题的条件和结论
(2)找推式,判断p→q 和q→p 的真假
(3)根据条件和推式得出结论
将命题转化成为另一个与之等价的且便于判断真假的命题
对于选择题,可以取一些特殊值或者特殊情况,用来说明
结论或者推导不成立,但不可用于证明题。
3怎么判断充要条件 有哪些方法
【2】等价法
【3】赋值法
【1】定义法:
3怎么判断充要条件 有哪些方法
【3】集合法:列出集合A={x|p(x)}和集合B={x|q(x)},利用集合的
包含关系来判断,如图:
ACB且BtA
p 是q的既不充分也不必要条件
BCA
p 是q 的必要不充分条件
AEB
p 是q 的充分不必要条件
A=B
p 是q的充要条件
1.指出下列各组中p是q的什么条件。
①p:(x-2)(x-3)=0;q:x-2=0
【解】化 简 ,p:x∈{2,3};q:x∈{2}, 则q代表的集合Q是p代表的集合P
的真子集,即Q 车P, 所 以p是q的必要不充分条件
②p:四边形的对角线相等;q: 四边形是矩形
【解】对角线相等的四边形不一定是矩形,p≠q;
矩形的对角线相等,q>p, 所 以p 是q的必要不充分条件
课堂练习
(1)充分条件与必要条件都有传递性,具体如下:
①若p=q,q>s 则有p=s, 即 p是s的充分条件;
②若s=q,q>p 则有s=p, 即 p是s的必要条件;
③若p→q,q→s, 则有p s, 即 p是s的充要条件;
(2)给定命题“若p, 则q”, 对于p是q的什么条件的证明:
①证明充分性,则需证明p=q;
②证明必要性,则需证明q>p;
4充分条件与必要条件的传递性
【问题】已 知p,q 都是r 的充分条件,s是r 的必要条件,q是s的必要条件,那么:
①s是q的什么条件 ②r是q的什么条件 ③p是q的什么条件
【解】利用图示,表示出p,q,s,r 之间的关系如下:
①因为q>r,r=s, 所以q=s; 又 有s=q, 所以s是q的充要条件
②因为r=s,s=q, 所以r=q; 又 有q=r, 所以r 是q的充要条件
③因为p=r,r→s,s>q, 所以p>q; 又有q≠p, 所 以p是q的充分不必要条件
4充分条件与必要条件的传递性
1.下列各组题中,哪些p是q 的充要条件 为什么
①p: 三角形为等腰三角形,q:三角形存在两角相等;
【解】因为p和q代表的都是等腰三角形,所以p=q,
即p q,p 是q的充要条件;
② p:圆O 内两条弦相等,q:圆O 内两条弦所对的圆周角相等;
【解】圆0内两条弦相等,则它们所对的圆周角相等或互补,因此p≠q,
所以p不是q的充要条件;
课堂练习
5本节考试常考什么 【充分条件,必要条件,充要条件的判断】 【题1·定义法】判断下列各题中p是q的什么条件
①p:x-3=0,q:(x-2)(x-3)=0;
【解】因为x-3=0→ (x-2)(x-3), 但(x-2)(x-3)≠x-3=0,
所以p是q的充分不必要条件;
②p:两个三角形相似,q:两个三角形全等;
【解】因为相似不一定全等,但全等一定相似,即p≠q,q>p,
所以p是q的必要不充分条件;
③p:x=y,q:x+t=y+t;
【解】因为由p推导到q和由q 推导到p 都是等式的基本性质,所以p→q且q>p,
所以p是q的充要条件.
【题2·集合法】判断下列各图中A是B的什么条件
【解】因为BSA, 所 以A是B的充分不必要条件
5本节考试常考什么
【解】因为A≠B且BCA, 所以A是B的既不充分也不必要条件
【解】因为A=B, 所 以A是B的充要条件
【充分条件,必要条件,充要条件的判断】
③
②
【题3·传递法】已知p是r的充分不必要条件,q是r的充分条件,s是r的必要条件,
q是s的必要条件,则p是q的什么条件
【解】由题意有p>r,r≠p,q=r,r→s,s=q, 所以p>r→S→q,
而 ,q=r≠p, 即p是q的充分不必要条件,
【注意】本题也可以用图形法,列出p,q,r,s 的关系图:
5本节考试常考什么
在图中路径p=r→s→q可以走通,但q=r≠p 走不通,同样可以得出结论.
【充分条件,必要条件,充要条件的判断】
p
牛
Y q
S
回顾复习
1.充分条件、必要条件:“若p, 则q”为真命题,是指由p可以推导出q, 记 作 :p>q, 并且说p是q的充分条件;q是p的必要条件。
2.充要条件:如果p可以推导出q, 并且q也可以推导出p, 即p=q, 且有q→p, 则相当于p=q 或者q p, 称作q是p的充分必要条件,q也是p的充分必要条件,简称充要条件。
3.判断充要条件的方法:(1)定义法;(2)等价法;(3)赋值法;(4)集合法
4.给定命题“若p, 则q”, 对于p是q的什么条件的证明:
①证明充分性,则需证明p=q;②证明必要性,则需证明q=p;
下课
第1章集合与常用逻辑用语
1.5 全称量词与存在量词
人教A 版2019高中数学必修第一册
1全称量词与全称量词命题
下列语句是命题吗 比较(1)和(3),(2)和(4),你有什么发现
(1)x>3 (2)2x+1 是整数
(3)对所有的x∈R,x>3; (4) 对任意一个x∈Z,2x+1 是整数
可以发现,语句(1)(2)中含有变量x, 由于不知道x的值,所以无法判断它们的
真假,所以(1)(2)不是命题;而(3)(4)在(1)(2)的基础上对变量x进行了限 定,用了“任意一个”条件,所以(3)(4)可以判断真假,它们是命题。
短语“所有的““任意一个”在逻辑中一般叫做全称量词,用符号“v”
表示,含有全称量词的命题,叫做全称量词命题;例如命题“对任意的x ∈Z, 2x+1 是奇数““所有的正方形都是矩形”都是全称量词命题
1全称量词与全称量词命题
通常,将含有变量x的语句用p(x),q(x),r(x)等等来表示,变量x的范围
用M 表示。那么,全称量词命题“对M 中任意一个x,p(x) 成立”可用符号简
记为
Vx∈M,p(x)
常见的全称量词有“一切”“每一个”“任给““所有的“
“全部的”“只要是”“任意的”“凡是”等等
Vx∈N,
x>0
我能判断真假,
而且是假命题!
我不能判断真 假,不是命题
x>0
【2】一个全称量词命题可以表示包含多个变量,如“Vx∈R,y∈R ,x +y ≥0”
【3】全称量词命题中一般含有全称量词,但是有些全称量词命题
中的全称量词是省略的,理解时需要把它补充出来,例如“平行四 边形的对角线互相平分”应理解为“所有的平行四边形对角线都互 相平分”
1全称量词与全称量词命题
【1】从集合的观点来看,全称量词命题是陈述某个集合中的所有元
素都具有某种相同的性质。因此,全称量词表示的数量可以是无限 的,也可以是有限的。这取决于所描述的这个集合中的元素的个
数。
课堂练习
请用不同表述方法表示全称量词命题“Vx∈M,p(x)”
【解】表述①:对所有的x∈M,p(x)成立
表述②:对一切x∈M,p(x)成立
表述③:对每一个x∈M,p(x)成立
表述④:任选一个x∈M,p(x)成立
表述⑤:凡是x∈M,p(x)成立
要判断全称量词命题“Vx∈M,p(x)” 是真命题,需要对集合中每
一个元素x, 证 明p(x) 成立;如果在集合中找到一个元素x , 使 得p(x) 不 成立,那么这个全称量词命题就是假命题.
它为真,我
要好好说明 下;它为假, 我一个反例 就说明了!
★要判断全称量词命题是假命
题,只需找一个反例即可.
★要判断全称量词命题是真命
题,需要从左往右地推导;
2全称量词命题怎么判断真假
全称 量词 命 题
也就是说,
2全称量词命题怎么判断真假
【例题】判断下列全称量词命题的真假
(1)所有的素数都是奇数;
【解】2是素数,但是2不是奇数,所以命题为假.
(2)Vx∈ R,|x|+1≥1;
【解】因为Vx∈R,|x|≥0, 所以|x|+1≥1, 命题为真
(3)对任意一个无理数x,x 也是无理数.
【解】因为 √2是无理数,但是(√2) = 2是有理数,
所以命题为假.
温肆提示
素数,即质数,
一个正整数,除 了1和自身之外 没有其他整数的 因数,则成为素
数(质数) .
课堂练习
判断下列全称量词命题的真假:
①每个四边形的对角线都互相垂直
【解】右图所示的四边形对角线就不垂直,
所以命题为假.
②Vxe{y|y是无理数},x 是无理数
【解】右x=33 是无理数,但x =( √3) =3
是有理数,所以命题为假;
③任何实数都有算术平方根
【解】-4是实数,但是-4没有算术平方根,
所以命题为假;
温留提示
非负数才有平方
根和算术平方根;负 数没有平方根,更没 有算术平方根.
3存在量词与存在量词命题
下列语句是命题吗 比较(1)和(3),(2)和(4),它们之间有什么关系
(1)2x+1=3; (2)x 能被2和3整除
(3)存在 一 个x∈R, 使2x+1 =3;(4) 至少有一个x ∈Z,x 能被2和3整除
可以发现, (1)(2)不是命题,而(3)在(1)的基础上,用短语
“存在一个”对变量的x取值进行了限定; (4)在(2)的基础上,用短语 “至少有一个”对变量的取值进行了限定;所以(3)(4)可以判断真假, 因此它们是命题。
短语“存在一个”“至少有一个”在逻辑中一般叫做存在量词,用符号
“3”表示,含有存在量词的命题,叫做存在量词命题;例如命题“有的平行 四边形是菱形”“存在不是素数的奇数”等都是存在量词命题.
3存在量词与存在量词命题
通常,将含有变量x的语句用p(x),q(x),r(x) 等等来表示,变量x的范围
用M表示。那么,存在量词命题 “M中存在一个x,p(x) 成立”可用符号简
记为
3x∈M,p(x)
常见的存在量词有“存在”“某一个”“任给”“对部分“
“对某个““对某些““有一个““有的”等 等
3x∈N,
x>0
我能判断真假, 而且是真命题!
我不能判断真 假,不是命题
x>0
【3】含有存在量词“存在”“有一个”等的命题,或虽没有写出存 在量词,但其意义具备“存在”“有一个”等特征的命题都是存在 性命题.
【4】一个存在量词命题中可以包含多个变量,如“3a,b使(a +b) =(a-b) ”.
【1】从集合的观点来看,存在量词命题是陈述某个集合中的某些 (个)元素所具有的某种性质。
【2】含有存在量词的命题,不管包含的程度有多大,都是存在量词 命题.如“存在无数个x∈R, 使x-1>0” 中,无数个也不能代表每 一个.
3存在量词与存在量词命题
课堂练习
请用不同表述方法表示存在量词命题“3x∈M,p(x)”
【解】表述①:至少有一个x ∈M,p(x)成立
表述②:存在x ∈M,p(x) 成立
表述③:对有些x ∈M,p(x)成立
表述④:对某个x ∈M,p(x) 成立
表述⑤;有一个x ∈M,p(x) 成立
要判断全称量词命题“3x∈M,p(x)” 是真命题,只需在集合M 中 找
到一个元素x, 证 明p(x)成立即可;如果在集合M 中找不到任何元素,使 得p(x) 成立,那么这个存在量词命题就是假命题.
★要判断存在量词命题是真命
题,只需要找出一个x满足条
件 ;
★要判断全称量词命题是假命
题,需要推导证明.
它为真,我 只要找出一 个例子就可 以;它为假, 我得证明!
4存在量词命题怎么判断真假
全称 量词 命 题
也就是说,
4存在量词命题怎么判断真假
【例题】判断下列存在量词命题的真假 (1)存在一个四边形的内角和是180°;
【解】所有四边形内角和为360°,所以命题为假.
(2)至少有一个整数n; 使得n -n 是奇数;
【解】因为n -n= n(n-1), 它是两个连续整数
的乘积,结果是偶数,所以命题为假;
(3)存在一个无理数x,x 是有理数.
【解】因为√2是无理数,( √2) =2是有理数,
所以命题为真.
无理数的平方,有
可能是有理数,如 √2,
( √2) =2;也有可能
是无理数,如
√3- √2,它的平方是3
- √2,还是无理数.
温留提示
②平面内存在一对有交点的平行线
【解】右平面内两条直线平行则没有交点,所以命题为假.
③有些平行四边形是菱形
【解】菱形是特殊的平行四边形,所以命题为真
温留提示
平面内两条直线的
位置关系有三种:
①平行,没有交点;
②相交,有一个交点;
③重合,有无数个交点.
课堂练习
判断下列存在量词命题的真假:
①有一个实数x, 使得x +2x-3=0
【解】右x=1 时 ,x +2x-3=1+2-3=0,
所以命题为真.
【例题】已知方程(a +5)x +2(a+1)x+a-5=0
(1)若3a ∈R, 使方程有一个实根,求a的取值范围.
【解】当a+5=0 即a=-5 时,方程化为-8x-10=0, 方程有 ,满足题意; 当a+5≠0 即a≠5 时,方程为一元二次方程,方程有解等价于△≥0,
即△=[2(a+1)] -4(a+5)(a-5)≥0, 解得a≥-13
综上,a≥-13
( 2 ) 若Va∈M, 方程无解,求集合M
【解】由(1)知方程无解等价于△<0,即△=[2(a+1)] -4(a+5)(a-5)<0,
解得a<-13, 所 以M={a|a<-13}
5本节考试常考什么
【含有一个量词的命题求参数间题】
1.全称量词命题“对M 中任意一个x,p(x) 成立”可用符号简记为:Vx∈M,p(x)
2.判断全称量词命题的真假:
★要判断全称量词命题是真命题,需要从左往右地推导;
★要判断全称量词命题是假命题,只需找一个反例即可.
3.存在量词命题“M 中存在一个x,p(x) 成立”可用符号简记为:3 x∈M,p(x)
4.判断存在量词命题的真假:
★要判断存在量词命题是真命题,只需要找出一个x满足条件; ★要判断全称量词命题是假命题,需要推导证明.
回顾复习
下 课
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
