高中数学人教B版(2019)选择性必修第一册第一章1.2.4二面角(1)课件(共19张PPT)
文档属性
| 名称 | 高中数学人教B版(2019)选择性必修第一册第一章1.2.4二面角(1)课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-06 19:30:01 | ||
图片预览






文档简介
(共29张PPT)
二面角(1) 高二年级数学
知识概要
一、二面角的相关概念
二 、二面角的度量
三 、例题分析与讲解
四 、课堂小结
情境与问题
日常生活中,很多场景都有平面与平面所成一定角度
的形象.
情境与问题
如何刻画这样的角的大小呢
二面角的相关概念
平面内的一条直线把一个平面分成两部分,其中的每一
部分都称为一个半平面.
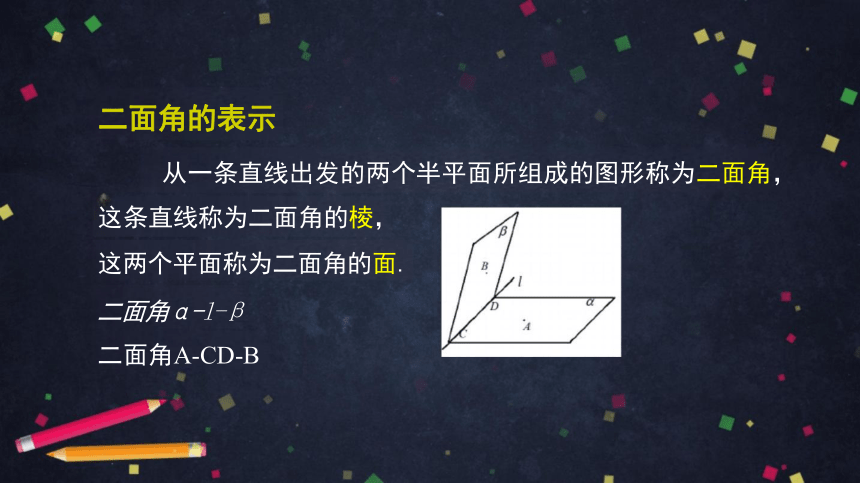
二面角的表示
从一条直线出发的两个半平面所组成的图形称为二面角,
这条直线称为二面角的棱,
这两个平面称为二面角的面.
二面角α-l-β
二面角A-CD-B
二面角的平面角
类比二面角和平面角,如何计算二面角的大小
二面角的平面角
类比二面角和平面角,如何计算二面角的大小
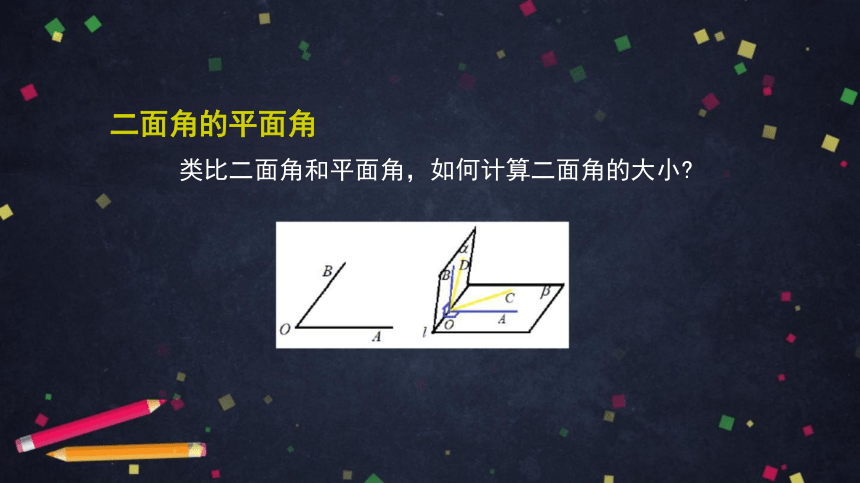
二面角的平面角
在二面角a-l-β 的棱上任取一点O, 以 O为垂足,分别在
半平面α和p 内作垂直于棱的射线OA 和OB, 则射线OA 和OB
所成的角称为二面角的平面角.
作二面角的平面角
已知平面α内一点A,
(1)过A作AB⊥β 于B,
(2)在平面α内,过A 作AC⊥1与C,
(3)连接BC.
∠ACB即为所求作二面角α-l-β 的
平面角.
二面角的大小
我们约定,二面角及其平面角的大小为[0,π].
直二面角
平面角是直角的二面角是直二面角.
证明a⊥
例题分析与讲解
例1.如图三棱锥S-ABC中,面SAC⊥面ABC, SA=SC=√3,AB=BC=2 且AB⊥BC.
求(1)二面角S-AB-C的大小;
(2)二面角B-SA-C的大小.
解:取AC,AB的中点D,E.
连接SD,DE,SE.
因为SA=SC, 所 以SD⊥AC.
又因为面SAC⊥ 面ABC,
所以SD⊥ 面ABC.
例题分析与讲解
(1)求二面角S-AB-C 的大小.
所以SE在平面ABC内的射影为DE.
因为DE为△ABC的中位线,AB⊥BC,
所以AB⊥DE.
从而由三垂线定理可知AB⊥SE.
所以∠SED为二面角S-AB-C的平面角
例题分析与讲解
(1)求二面角S-AB-C的大小.
由AB=BC=2 且AB⊥BC 可知AC=2 √2,
所 又DE=_BC=1
又因为SD=√ SA -AD =√3-2=1,
9
例题分析与讲解
(1)求二面角S-AB-C的大小.
∠SED=45°, 即二面角S-AB-C 的大小为45°.
在△SDE中,
例题分析与讲解
(2)求二面角B-SA-C的大小.
解:连接BD.
因为BA=BC, 所以BD⊥AC.
又因为面SAC⊥ 面ABC,
所以BD⊥ 面SAC.
过D作DF⊥SA于F, 连接BF.
所以BF在平面SAC的射影为DF.
因为DF⊥SA,
由三垂线定理可知BF⊥SA,
所以∠BFD为二面角B-SA-C的平面角.
例题分析与讲解
(2)求二面角B-SA-C的大小.
例题分析与讲解
(2)求二面角B-SA-C的大小.
因为SD=1,AD=√2,SA=√3,
由AAD的面积的求法可知or-
而BD=Ac=√2所以tan ∠BFD=BP-√3,
所以∠BFD=60°, 即二面角B-SA-C为60°.
例题分析与讲解
例2.已知正方体ABCD-A,BC D, 棱长为1.
(1)求二面角D -AC -B的余弦值;
(2)求二面角D-A,B-C 的余弦值.
例题分析与讲解
(1)求二面角D -AC -B的余弦值.
观察发现二面角D -AC -B是钝角,
与二面角B-AC -B互补.
解:连接BD 交AC 于0,连接BO.
因为BB ⊥ 面A,BC D, 而BD ⊥AC, 所以BO1 AC,
∠BOB是二面角B -AC -B的平面角.
例题分析与讲解
(1)求二面角D -AC -B的余弦值.
例题分析与讲解
(1)求二面角D -AC -B的余弦值
设二面角D -AC -B的平面角为θ,
θ=π- ∠BOB,
tanθ=-tan ∠BOB =-√2.
由同角关系得
即=面角DAG,蹦余磁信为
观察图形,正方体截面A,BC和截面DAB
均是正三角形.
例题分析与讲解
(2)求二面角D-A,B-C的余弦值.
解:取A,B的中点E, 连接DE,C E,C D.
所以C E⊥A B,DEI AB,
所以∠DEC 是二面角D-A,B-C的平面角.
例题分析与讲解
(2)求二面角D-AB-C的余弦值.
D=√2.
在△EDC中,由余弦定理得cos ∠DE
即二面角D-A,B-C 的余弦值为一 3
,
C
为
又
高
6
2
CE
长为
所以DE
正三角形
例题分析与讲解
(2)求二面角D-A,B-C的余弦值
课堂小结
1.二面角的表示:面-棱-面
2.二面角的度量:求二面角的平面角.
关注作二面角的平面角的方法、三垂线定理及其逆定理
的使用.
3.灵活运用空间几何平面化的思想,把二面角的平面角
放到三角形里求解.
课后练习
1.通读课本;
2.完成课本习题:第52页练习A1; 练 习B2,3.
0已知二面角P-AB-P '的大小为 垂 且PP'⊥ 面ABP',△ABP 的面积为3,求
△ABP'的面积.
② 已知正三棱锥S-ABC 的所有棱长都为1,求其侧面与底面所 成角的余弦值.
③ 如图,已知 AB 是圆的直径,且AB=4,PA 垂直于圆所在的 平面,且PA=2√3,M 是圆周上一点,且∠ABM=30°, 求 二面角A-BM-P 的大小
(第3题)
谢谢
二面角(1) 高二年级数学
知识概要
一、二面角的相关概念
二 、二面角的度量
三 、例题分析与讲解
四 、课堂小结
情境与问题
日常生活中,很多场景都有平面与平面所成一定角度
的形象.
情境与问题
如何刻画这样的角的大小呢
二面角的相关概念
平面内的一条直线把一个平面分成两部分,其中的每一
部分都称为一个半平面.
二面角的表示
从一条直线出发的两个半平面所组成的图形称为二面角,
这条直线称为二面角的棱,
这两个平面称为二面角的面.
二面角α-l-β
二面角A-CD-B
二面角的平面角
类比二面角和平面角,如何计算二面角的大小
二面角的平面角
类比二面角和平面角,如何计算二面角的大小
二面角的平面角
在二面角a-l-β 的棱上任取一点O, 以 O为垂足,分别在
半平面α和p 内作垂直于棱的射线OA 和OB, 则射线OA 和OB
所成的角称为二面角的平面角.
作二面角的平面角
已知平面α内一点A,
(1)过A作AB⊥β 于B,
(2)在平面α内,过A 作AC⊥1与C,
(3)连接BC.
∠ACB即为所求作二面角α-l-β 的
平面角.
二面角的大小
我们约定,二面角及其平面角的大小为[0,π].
直二面角
平面角是直角的二面角是直二面角.
证明a⊥
例题分析与讲解
例1.如图三棱锥S-ABC中,面SAC⊥面ABC, SA=SC=√3,AB=BC=2 且AB⊥BC.
求(1)二面角S-AB-C的大小;
(2)二面角B-SA-C的大小.
解:取AC,AB的中点D,E.
连接SD,DE,SE.
因为SA=SC, 所 以SD⊥AC.
又因为面SAC⊥ 面ABC,
所以SD⊥ 面ABC.
例题分析与讲解
(1)求二面角S-AB-C 的大小.
所以SE在平面ABC内的射影为DE.
因为DE为△ABC的中位线,AB⊥BC,
所以AB⊥DE.
从而由三垂线定理可知AB⊥SE.
所以∠SED为二面角S-AB-C的平面角
例题分析与讲解
(1)求二面角S-AB-C的大小.
由AB=BC=2 且AB⊥BC 可知AC=2 √2,
所 又DE=_BC=1
又因为SD=√ SA -AD =√3-2=1,
9
例题分析与讲解
(1)求二面角S-AB-C的大小.
∠SED=45°, 即二面角S-AB-C 的大小为45°.
在△SDE中,
例题分析与讲解
(2)求二面角B-SA-C的大小.
解:连接BD.
因为BA=BC, 所以BD⊥AC.
又因为面SAC⊥ 面ABC,
所以BD⊥ 面SAC.
过D作DF⊥SA于F, 连接BF.
所以BF在平面SAC的射影为DF.
因为DF⊥SA,
由三垂线定理可知BF⊥SA,
所以∠BFD为二面角B-SA-C的平面角.
例题分析与讲解
(2)求二面角B-SA-C的大小.
例题分析与讲解
(2)求二面角B-SA-C的大小.
因为SD=1,AD=√2,SA=√3,
由AAD的面积的求法可知or-
而BD=Ac=√2所以tan ∠BFD=BP-√3,
所以∠BFD=60°, 即二面角B-SA-C为60°.
例题分析与讲解
例2.已知正方体ABCD-A,BC D, 棱长为1.
(1)求二面角D -AC -B的余弦值;
(2)求二面角D-A,B-C 的余弦值.
例题分析与讲解
(1)求二面角D -AC -B的余弦值.
观察发现二面角D -AC -B是钝角,
与二面角B-AC -B互补.
解:连接BD 交AC 于0,连接BO.
因为BB ⊥ 面A,BC D, 而BD ⊥AC, 所以BO1 AC,
∠BOB是二面角B -AC -B的平面角.
例题分析与讲解
(1)求二面角D -AC -B的余弦值.
例题分析与讲解
(1)求二面角D -AC -B的余弦值
设二面角D -AC -B的平面角为θ,
θ=π- ∠BOB,
tanθ=-tan ∠BOB =-√2.
由同角关系得
即=面角DAG,蹦余磁信为
观察图形,正方体截面A,BC和截面DAB
均是正三角形.
例题分析与讲解
(2)求二面角D-A,B-C的余弦值.
解:取A,B的中点E, 连接DE,C E,C D.
所以C E⊥A B,DEI AB,
所以∠DEC 是二面角D-A,B-C的平面角.
例题分析与讲解
(2)求二面角D-AB-C的余弦值.
D=√2.
在△EDC中,由余弦定理得cos ∠DE
即二面角D-A,B-C 的余弦值为一 3
,
C
为
又
高
6
2
CE
长为
所以DE
正三角形
例题分析与讲解
(2)求二面角D-A,B-C的余弦值
课堂小结
1.二面角的表示:面-棱-面
2.二面角的度量:求二面角的平面角.
关注作二面角的平面角的方法、三垂线定理及其逆定理
的使用.
3.灵活运用空间几何平面化的思想,把二面角的平面角
放到三角形里求解.
课后练习
1.通读课本;
2.完成课本习题:第52页练习A1; 练 习B2,3.
0已知二面角P-AB-P '的大小为 垂 且PP'⊥ 面ABP',△ABP 的面积为3,求
△ABP'的面积.
② 已知正三棱锥S-ABC 的所有棱长都为1,求其侧面与底面所 成角的余弦值.
③ 如图,已知 AB 是圆的直径,且AB=4,PA 垂直于圆所在的 平面,且PA=2√3,M 是圆周上一点,且∠ABM=30°, 求 二面角A-BM-P 的大小
(第3题)
谢谢
