2.1 函数y=Asin(ωχ+φ) 课件(共36张PPT)高中数学人教A版2019选择性必修一册
文档属性
| 名称 | 2.1 函数y=Asin(ωχ+φ) 课件(共36张PPT)高中数学人教A版2019选择性必修一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-06 19:31:01 | ||
图片预览








文档简介
(共36张PPT)
人教2019A版必修第一册
第五章 三角函数
5.6函数y=Asin(ox+φ) 的图像
学习目标
1.理解参数A,w,φ 对函数y=Asin(ox+φ) 的图象的影响;能够将y=sin
x 的图象进行交换得到y=Asin(wx+φ),x∈R 的图象 .(难点)
2.会用“五点法”画函数 y=Asin(wx+φ) 的简图;能根据y=Asin(wx+φ)
的部分图象,确定其解析式.( 重点)
3.求函数解析式时φ值的确定.(易错点)
上面我们利用三角函数的知识建立了一个形如y=Asin(wx+φ) 其中(A>0,
w>0) 的函数.显然,这个函数由参数A,@,φ 所确定 . 因此,只要了
解这些参数的意义,知道它们的变化对函数图象的影响,就能把握这个函数的性 质 .
提出问题
从解析式看,函数y=cosx 就是函数y=Asin(wx+φ)
在A=1 ,w=1,φ=0 时的特殊情形.
(1)能否借助我们熟悉的函数 y=sinx 的图象与性质研究参数A,@,φ
对函数y=Asin(wx+φ) 的影响
(2)函数y=Asin(wx+φ) 含有三个参数,你认为应按怎样的思路进行研究.
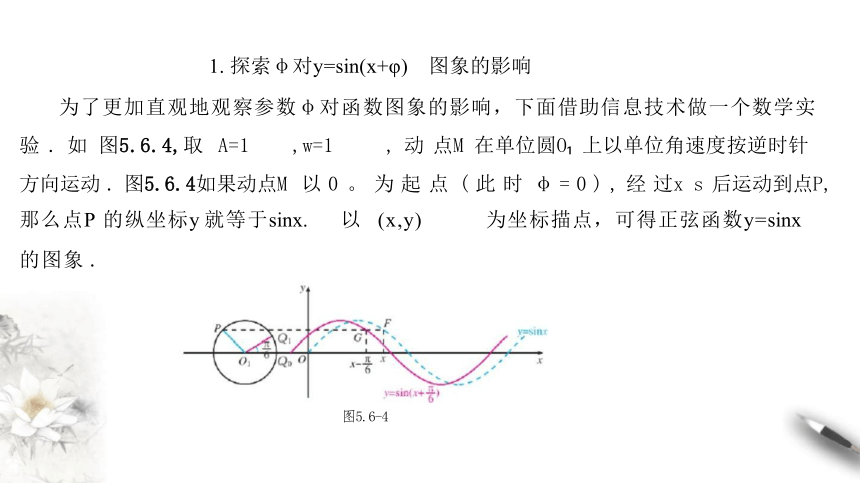
1. 探索φ对y=sin(x+φ) 图象的影响
为了更加直观地观察参数φ对函数图象的影响,下面借助信息技术做一个数学实
验 . 如 图5.6.4,取 A=1 ,w=1 , 动 点M 在单位圆O 上以单位角速度按逆时针
方向运动 . 图5.6.4如果动点M 以 0 。 为 起 点 ( 此 时 φ = 0 ) , 经 过x s 后运动到点P,
那么点P 的纵坐标y 就等于sinx. 以 (x,y) 为坐标描点,可得正弦函数y=sinx
的图象 .
图5.6-4
当起点位于Q 时 , , 可 得 函 的图象 . 进
一步,在单位圆上,设两个动点分别以Q 。,Q 为起点同时开始
运 动 . 如 果 以Q 为起点的动点到达圆周上点P的时间为x s , 那么
以Q 为起点的动点相继到达点P 的时间是 这个规律反映
在图象上就是:如果F(x,y) 是函数y=sinx 图象上的一点,
那么 就是函数 图象上的点,如图5.6-4所
示 . 这说明,把正弦曲线y=sinx 上的所有点向左平移 个单位长
在单位圆上拖动起点Q , 使 点Q 绕点Q 旋转 到Q , 你发现图象有什么
变化 如果使点Q。绕 点Q 旋转- ,-3, 或者旋转一个任意角φ呢
分别说一说旋 转 酬 时的 情况 .
度,就得到
的图象 .
!
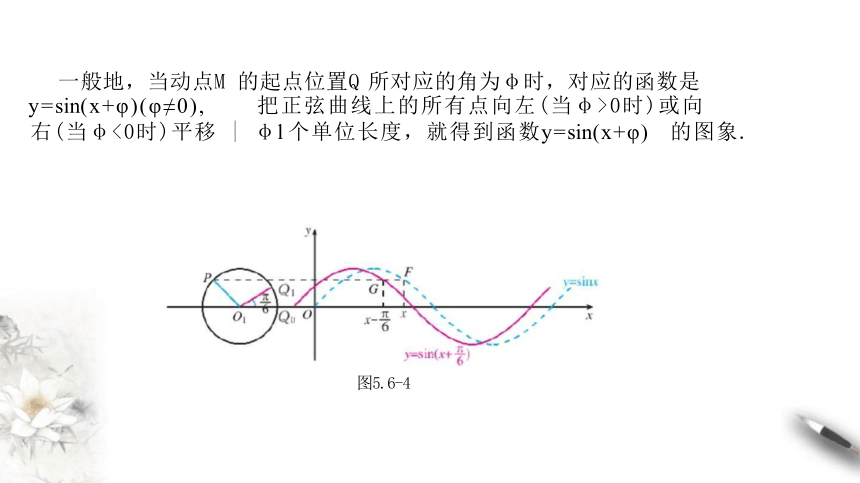
一般地,当动点M 的起点位置Q 所对应的角为φ时,对应的函数是
y=sin(x+φ)(φ≠0), 把正弦曲线上的所有点向左(当φ>0时)或向
右(当φ<0时)平移 | φl 个单位长度,就得到函数y=sin(x+φ) 的图象.
图5.6-4
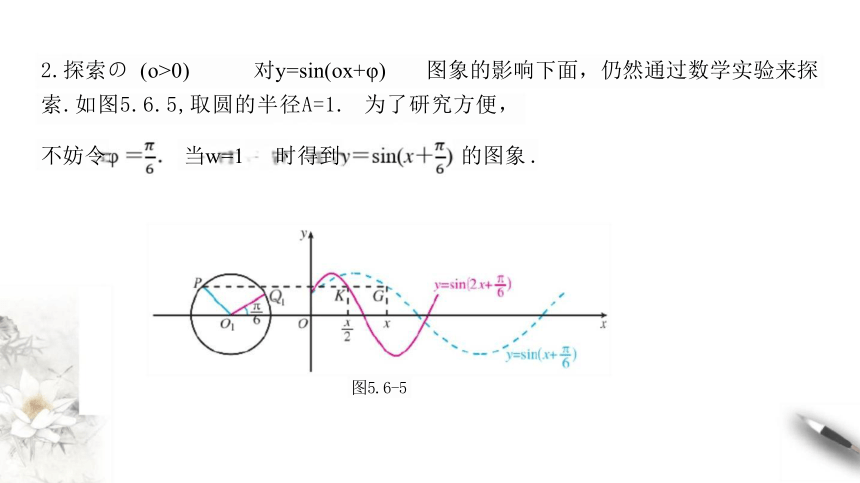
2.探索の (o>0) 对y=sin(ox+φ) 图象的影响下面,仍然通过数学实验来探
索.如图5.6.5,取圆的半径A=1. 为了研究方便,
不妨令 当w=1 时得到 的图象 .
图5.6-5
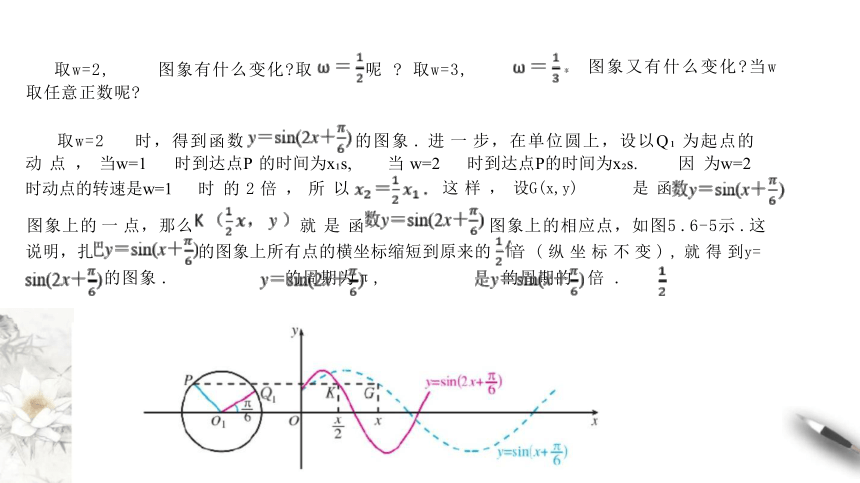
取w=2 时,得到函数 的图象 . 进 一 步,在单位圆上,设以Q 为起点的 动 点 , 当w=1 时到达点P 的时间为x s, 当 w=2 时到达点P的时间为x s. 因 为w=2
时动点的转速是w=1 时 的 2 倍 , 所 以 这 样 , 设G(x,y) 是 函
图象上的 一 点,那么 就 是 函 图象上的相应点,如图5 .6-5示 .这 说明,扎 的图象上所有点的横坐标缩短到原来的 音 ( 纵 坐 标 不 变 ) , 就 得 到y= 的图象 . 的周期为π, 的周期的 倍 .
取w=2, 图象有什么变化 取 呢 取w=3, 取任意正数呢
事 图象又有什么变化 当w
同理,当 时,动点的转速是w=1 时的 倍,以Q 为起点,到达点P的时间 是w=1 时 的 2 倍 . 这 样 , 图象上所有点的横坐标扩大到原来的2倍 (纵坐标不变),就得到 的图象 . 的周期为4π,
的周期的2倍 .
一般地,函数的周期 把y=sin(x+φ) 图象上所有点的横坐标缩短(当w>1 时 ) 或 伸 长 ( 当 0说一说 w=3,
时的情 况 .
3.探索A(A>0) 对 y=sin(ox+φ) 图象的影响
下面通过数学实验探索A对函数图象的影响.为了研究方便,不妨令o=2,φ=
当A=1 时,如图5.6.6,可得 的图象 .
改变A的取值,
使A 取 2 , ,3, 等 , 你发现图象有什么变化 当A 取任意正数呢
图5.6-6
事
当A=2 时,得到函数 的图象.
进一步,设射线O Q 与以O 为圆心、2为半径的圆交于T . 如果单位圆上以O 为
起点的动点,以w=2 的转速经过xs 到达圆周上点P, 那么点P的纵坐标是2sin
);相应地,点T 在以O 为圆心、2为半径的圆上运动到点T, 点 T的纵
坐标是 . 这 样 , 设K(x,y) 是函数 图象上的一点,
就是函数图象 上的相应点,如图5.6.6所示.这
图象上所有点的纵坐标伸长到原来的2倍(横坐标不变),
的图象.
那么点N(x,2y)
说明,把
一 般地,函数y=Asin(wx+φ) 的图象,可以看作是把y=Asin(ox+φ) 图象上所有点的纵坐标伸
长 ( 当A>1 时 ) 或 缩 短 ( 当 0函数y=Asin(ox+φ) 的 值 域 是 [ -A,A], 最大值是A, 最小值是一 A
图象上所有点的纵坐标缩短到原来的
倍 ( 横 坐 标 不 变 ) ,
同理,托
的图象 .
一般地,函数y=Asin(ox+φ)(A>0,w>0) 的图象,可以用下面的方
法得到:先画出函数y=sinx 的图象;再把正弦曲线向左(或右)平移|φl个单位
长度,得到函数y=sin(x+φ) 的图象;然后把曲线上各点的横坐标变为原来的 倍 (纵坐标不变),得到函数y=sin(ox+φ)的图象;最后把曲线上各点的纵坐标变为 原来的A倍(横坐标不变),这时的曲线就是函数y=Asin(ox+φ) 的图象 .
你能总结一下从正弦函数图象出发,通过图象变换得到y=Asin(ox+φ)(A>0,w>0) 图象的过程与方法吗
横坐标缩短o>1 (伸长0纵坐标不变
横坐标不变
纵坐标伸长A>1 (缩短0y=sin(x+φ)
y=sin(ox+φ)
y=Asin(ox+φ)
总结: y=sinx → y=Asin(ox+φ)
方法1:(按φ,w,A 顺序变换)
向左φ>0(向右φ<0)
平移Iφl个单位
y=sinx
横坐标缩短o>1 (伸长0y=sinx
纵坐标不变
纵坐标伸 长A>1(缩短0→y=Asin(ox+φ)
方法2:(按按 w,φ, A顺序变换)
→ y=sinox
横坐标不变
y=Asin(ox+φ)
总结:
y=sinx
典例解析
例 1 画出函数 的简图 .
解:先画出函数y=sinx的图象;再把正弦曲线向右平移 个单位长度,
得到函数的图象;然后使曲线上各点的横坐标变为原来的 倍,得到函数的图象;
最后把曲线上各点的纵坐标变为原来的2倍,这时的曲线就是函 的图象,如图5.6.7所示.
图5.6-7
X 0 π
2π
Y 0 2 0 -2
0
下面用“五点法”画函数 在一个周期
令 , 则
列表(表5 . 6 . 1),描点画图(图5 . 6 . 8)
内的图象 .
图5.6-8
表5.6-1
例2摩天轮是一种大型转轮状的机械建筑设施,游客坐在摩天轮的座舱
里慢慢地往上转,可以从高处俯瞰四周景色.如图5.6.9,某摩天轮最高
点距离地面高度为120m, 转盘直径为110m, 设置有48个座舱,开启
后按逆时针方向匀速旋转,游客在座舱转到距离地面最近的位置进舱,
转一周大约需要30min.
(1)游客甲坐上摩天轮的座舱,开始转动t min后距离地面的高度为H
m, 求在转动一周的过程中, H关于t 的函数解析式;
(2)求游客甲在开始转动5 min后距离地面的高度;
(3)若甲、乙两人分别坐在两个相邻的座舱里,在运行一周的过程
中,求两人距离地面的高度差h ( 单 位 :m) 关 于t 的函数解析式,并
求高度差的最大值(精确到0 . 1)
图5.6-9
解:如图5.6.10,设座舱距离地面最近的位置为点P,
以轴心0为原点,与地面平行的直线为x 轴建立直角坐标系.
( 1 ) 设t=0 min时,游客甲位于点P(0,-55),
以 OP为终边的角为 根据摩天轮转一周大约需要30 min,
可知座舱转动的角速度约为
由题意可得 ,0≤t≤30,
(2)当t=5时 ,
所以,游客甲在开始转动5 min 后距离地面的高度约为37.5m.
分析:摩天轮上的座舱运动可以近似地看作是质点在圆周上做匀速旋转.在旋转过程
中,游客距离地面的高度幫呈现周而复始的变化,因此可以考虑用三角函数来刻画.
图5.6-10
(3 )如图5.6.10,甲、乙两人的位置分别用点A,B表示,则
经过t min后甲距离地面的高度为
(或2),即t≈7.8(或22.8)时,h的最大值为
所以,甲、乙两人距离地面的高度差的最大值约为7.2m.
点B 相对于点A 始终落后 ,此时乙距离地面的高度
可得
1 1
达标检测
1. 函 数 的振幅和周期分别为( )
A.3,4 B.3,
C ,4 口 ,3
振 幅 是 3 , 周 期
由于函数
【答案】
【 解 析】
A
2.将函数 的图象上所有点的横坐标伸长到原来的2倍(纵坐标
不变),再将所得图象向左平移 个单位,则所得函数图象对应的解析式为( )
A
2倍,得 的图象,再将此图象向左平移 个单位,
【解析】 函数 的图象上所有点的横坐标伸长到原来的
【答案】 D
的图象,选D.
得
【解析】 由已知得A=3,
所以 故选 B.
【答案】 B
初相是 则这个函数的表达式是( )
的最大值是3,最小正周期
3. 已知函数y=Asin(ox+φ)(A>0,w>0)
事
事
事
4. 函 数 图象的一条对称轴是 . (填序号)
① ;②x=0;③ ;④
【解析】 由正弦函数对称轴可知.
,k∈Z,k=0
【 答案】 ③
k∈Z,
时 ,
5. 已知函数 ,x ∈R.
(1)写出函数 f(x)的对称轴方程、对称中心的坐标及单调区间;
(2)求函数f(x)在区间[0, 上的最大值和最小值.
k∈Z; 由 k∈Z 解得对称中心是 ,k∈Z; 由
解 得 单 调 递 增 区 间 由
解得单调递减区间
,k∈Z,
解 得 f(x)的 对 称 轴 方 程 是
【 解 】 (1)由
(2)∵ ,∴
∴当 即x=0 时 ,f(x) 取最小值为一1;
当 , 即 时 ,f(x) 取最大值为2.
事
课堂小结
1. 知识:如何采用两角和或差的正余弦公式进行合角,借助三角函数的相关性质求值.其中三
角函数最值问题是对三角函数的概念、图像和性质,以及诱导公式、同角三角函数基本关系、 和(差)角公式的综合应用,也是函数思想的具体体现.如何科学的把实际问题转化成数学问题, 如何选择自变量建立数学关系式;求解三角函数在某一区间的最值问题.
2.思想:本节课通过由特殊到一般方式把关系式y=asin x+bcosx化成y=Asin(@x+0)的形式,可
以很好地培养学生探究、归纳、类比的能力.通过探究如何选择自变量建立数学关系式,可
以很好地培养学生分析问题、解决问题的能力和应用意识,进一步培养学生的建模意识.
教材整理1 φ对函数y=sin(x+φ)
时,向_左 平移
y=sinx80 时,向右 平 移φ
的图象的影响
y=sin(x+φ
度
度
长
长
位
位
单
单
个
个
一、[基础·初探]
w>1 时,所有点的横坐标 缩短_到原来
1 y=sin(wx+φ
O教材整理2 w(w>0) 对函数y=sin(wx+φ) 的图象的影响
y=sin(x+φ)
纵 坐 标 _伸长_到原来的A 倍
→ y=Asin(wx+
点纵坐标 缩短_到原来的A_倍
教材整理3 A(A>0) 对y=Asin(wx+φ) 的图象的影响
横坐标变为原来的
纵坐标不变
y=Asin
_
1
2.正弦曲线到函数y=Asin(wox+φ) 的图象的变换过程:
的 图 象 纵坐标变为原来的A倍
y=
的图象.
或向右
个单位长度
y=sin x 的图象
向左(
平移
横坐标不变
_的图象
y= S]
振幅
它是做简谐运动的物体离开平衡位置的最大距离
周期
它是物体往复运动_ 一次所需要的时间
频率
它是单位时间内往复运动的 次数
相位 wx+φ
其中_ φ为初相
教材整理4 A,w,φ 的物理意义
在y=Asin(wx+φ),x∈[0, 十 一 ](A>0,w>0) 中,各参数的物理意义.
所有的点向左(φ>0) 或向右(φ<0)平行移动
lφl 个单位长度
横坐标缩短(o>1 )或
伸长(0纵坐标不变
纵坐标伸长(A>1 )或 缩短(0横坐标不变
y=sin(x+φ)
y=sinox
y=Asinx
y=sinx
y=sinx
y=sinx
人教2019A版必修第一册
第五章 三角函数
5.6函数y=Asin(ox+φ) 的图像
学习目标
1.理解参数A,w,φ 对函数y=Asin(ox+φ) 的图象的影响;能够将y=sin
x 的图象进行交换得到y=Asin(wx+φ),x∈R 的图象 .(难点)
2.会用“五点法”画函数 y=Asin(wx+φ) 的简图;能根据y=Asin(wx+φ)
的部分图象,确定其解析式.( 重点)
3.求函数解析式时φ值的确定.(易错点)
上面我们利用三角函数的知识建立了一个形如y=Asin(wx+φ) 其中(A>0,
w>0) 的函数.显然,这个函数由参数A,@,φ 所确定 . 因此,只要了
解这些参数的意义,知道它们的变化对函数图象的影响,就能把握这个函数的性 质 .
提出问题
从解析式看,函数y=cosx 就是函数y=Asin(wx+φ)
在A=1 ,w=1,φ=0 时的特殊情形.
(1)能否借助我们熟悉的函数 y=sinx 的图象与性质研究参数A,@,φ
对函数y=Asin(wx+φ) 的影响
(2)函数y=Asin(wx+φ) 含有三个参数,你认为应按怎样的思路进行研究.
1. 探索φ对y=sin(x+φ) 图象的影响
为了更加直观地观察参数φ对函数图象的影响,下面借助信息技术做一个数学实
验 . 如 图5.6.4,取 A=1 ,w=1 , 动 点M 在单位圆O 上以单位角速度按逆时针
方向运动 . 图5.6.4如果动点M 以 0 。 为 起 点 ( 此 时 φ = 0 ) , 经 过x s 后运动到点P,
那么点P 的纵坐标y 就等于sinx. 以 (x,y) 为坐标描点,可得正弦函数y=sinx
的图象 .
图5.6-4
当起点位于Q 时 , , 可 得 函 的图象 . 进
一步,在单位圆上,设两个动点分别以Q 。,Q 为起点同时开始
运 动 . 如 果 以Q 为起点的动点到达圆周上点P的时间为x s , 那么
以Q 为起点的动点相继到达点P 的时间是 这个规律反映
在图象上就是:如果F(x,y) 是函数y=sinx 图象上的一点,
那么 就是函数 图象上的点,如图5.6-4所
示 . 这说明,把正弦曲线y=sinx 上的所有点向左平移 个单位长
在单位圆上拖动起点Q , 使 点Q 绕点Q 旋转 到Q , 你发现图象有什么
变化 如果使点Q。绕 点Q 旋转- ,-3, 或者旋转一个任意角φ呢
分别说一说旋 转 酬 时的 情况 .
度,就得到
的图象 .
!
一般地,当动点M 的起点位置Q 所对应的角为φ时,对应的函数是
y=sin(x+φ)(φ≠0), 把正弦曲线上的所有点向左(当φ>0时)或向
右(当φ<0时)平移 | φl 个单位长度,就得到函数y=sin(x+φ) 的图象.
图5.6-4
2.探索の (o>0) 对y=sin(ox+φ) 图象的影响下面,仍然通过数学实验来探
索.如图5.6.5,取圆的半径A=1. 为了研究方便,
不妨令 当w=1 时得到 的图象 .
图5.6-5
取w=2 时,得到函数 的图象 . 进 一 步,在单位圆上,设以Q 为起点的 动 点 , 当w=1 时到达点P 的时间为x s, 当 w=2 时到达点P的时间为x s. 因 为w=2
时动点的转速是w=1 时 的 2 倍 , 所 以 这 样 , 设G(x,y) 是 函
图象上的 一 点,那么 就 是 函 图象上的相应点,如图5 .6-5示 .这 说明,扎 的图象上所有点的横坐标缩短到原来的 音 ( 纵 坐 标 不 变 ) , 就 得 到y= 的图象 . 的周期为π, 的周期的 倍 .
取w=2, 图象有什么变化 取 呢 取w=3, 取任意正数呢
事 图象又有什么变化 当w
同理,当 时,动点的转速是w=1 时的 倍,以Q 为起点,到达点P的时间 是w=1 时 的 2 倍 . 这 样 , 图象上所有点的横坐标扩大到原来的2倍 (纵坐标不变),就得到 的图象 . 的周期为4π,
的周期的2倍 .
一般地,函数的周期 把y=sin(x+φ) 图象上所有点的横坐标缩短(当w>1 时 ) 或 伸 长 ( 当 0
时的情 况 .
3.探索A(A>0) 对 y=sin(ox+φ) 图象的影响
下面通过数学实验探索A对函数图象的影响.为了研究方便,不妨令o=2,φ=
当A=1 时,如图5.6.6,可得 的图象 .
改变A的取值,
使A 取 2 , ,3, 等 , 你发现图象有什么变化 当A 取任意正数呢
图5.6-6
事
当A=2 时,得到函数 的图象.
进一步,设射线O Q 与以O 为圆心、2为半径的圆交于T . 如果单位圆上以O 为
起点的动点,以w=2 的转速经过xs 到达圆周上点P, 那么点P的纵坐标是2sin
);相应地,点T 在以O 为圆心、2为半径的圆上运动到点T, 点 T的纵
坐标是 . 这 样 , 设K(x,y) 是函数 图象上的一点,
就是函数图象 上的相应点,如图5.6.6所示.这
图象上所有点的纵坐标伸长到原来的2倍(横坐标不变),
的图象.
那么点N(x,2y)
说明,把
一 般地,函数y=Asin(wx+φ) 的图象,可以看作是把y=Asin(ox+φ) 图象上所有点的纵坐标伸
长 ( 当A>1 时 ) 或 缩 短 ( 当 0
图象上所有点的纵坐标缩短到原来的
倍 ( 横 坐 标 不 变 ) ,
同理,托
的图象 .
一般地,函数y=Asin(ox+φ)(A>0,w>0) 的图象,可以用下面的方
法得到:先画出函数y=sinx 的图象;再把正弦曲线向左(或右)平移|φl个单位
长度,得到函数y=sin(x+φ) 的图象;然后把曲线上各点的横坐标变为原来的 倍 (纵坐标不变),得到函数y=sin(ox+φ)的图象;最后把曲线上各点的纵坐标变为 原来的A倍(横坐标不变),这时的曲线就是函数y=Asin(ox+φ) 的图象 .
你能总结一下从正弦函数图象出发,通过图象变换得到y=Asin(ox+φ)(A>0,w>0) 图象的过程与方法吗
横坐标缩短o>1 (伸长0
横坐标不变
纵坐标伸长A>1 (缩短0
y=sin(ox+φ)
y=Asin(ox+φ)
总结: y=sinx → y=Asin(ox+φ)
方法1:(按φ,w,A 顺序变换)
向左φ>0(向右φ<0)
平移Iφl个单位
y=sinx
横坐标缩短o>1 (伸长0
纵坐标不变
纵坐标伸 长A>1(缩短0
方法2:(按按 w,φ, A顺序变换)
→ y=sinox
横坐标不变
y=Asin(ox+φ)
总结:
y=sinx
典例解析
例 1 画出函数 的简图 .
解:先画出函数y=sinx的图象;再把正弦曲线向右平移 个单位长度,
得到函数的图象;然后使曲线上各点的横坐标变为原来的 倍,得到函数的图象;
最后把曲线上各点的纵坐标变为原来的2倍,这时的曲线就是函 的图象,如图5.6.7所示.
图5.6-7
X 0 π
2π
Y 0 2 0 -2
0
下面用“五点法”画函数 在一个周期
令 , 则
列表(表5 . 6 . 1),描点画图(图5 . 6 . 8)
内的图象 .
图5.6-8
表5.6-1
例2摩天轮是一种大型转轮状的机械建筑设施,游客坐在摩天轮的座舱
里慢慢地往上转,可以从高处俯瞰四周景色.如图5.6.9,某摩天轮最高
点距离地面高度为120m, 转盘直径为110m, 设置有48个座舱,开启
后按逆时针方向匀速旋转,游客在座舱转到距离地面最近的位置进舱,
转一周大约需要30min.
(1)游客甲坐上摩天轮的座舱,开始转动t min后距离地面的高度为H
m, 求在转动一周的过程中, H关于t 的函数解析式;
(2)求游客甲在开始转动5 min后距离地面的高度;
(3)若甲、乙两人分别坐在两个相邻的座舱里,在运行一周的过程
中,求两人距离地面的高度差h ( 单 位 :m) 关 于t 的函数解析式,并
求高度差的最大值(精确到0 . 1)
图5.6-9
解:如图5.6.10,设座舱距离地面最近的位置为点P,
以轴心0为原点,与地面平行的直线为x 轴建立直角坐标系.
( 1 ) 设t=0 min时,游客甲位于点P(0,-55),
以 OP为终边的角为 根据摩天轮转一周大约需要30 min,
可知座舱转动的角速度约为
由题意可得 ,0≤t≤30,
(2)当t=5时 ,
所以,游客甲在开始转动5 min 后距离地面的高度约为37.5m.
分析:摩天轮上的座舱运动可以近似地看作是质点在圆周上做匀速旋转.在旋转过程
中,游客距离地面的高度幫呈现周而复始的变化,因此可以考虑用三角函数来刻画.
图5.6-10
(3 )如图5.6.10,甲、乙两人的位置分别用点A,B表示,则
经过t min后甲距离地面的高度为
(或2),即t≈7.8(或22.8)时,h的最大值为
所以,甲、乙两人距离地面的高度差的最大值约为7.2m.
点B 相对于点A 始终落后 ,此时乙距离地面的高度
可得
1 1
达标检测
1. 函 数 的振幅和周期分别为( )
A.3,4 B.3,
C ,4 口 ,3
振 幅 是 3 , 周 期
由于函数
【答案】
【 解 析】
A
2.将函数 的图象上所有点的横坐标伸长到原来的2倍(纵坐标
不变),再将所得图象向左平移 个单位,则所得函数图象对应的解析式为( )
A
2倍,得 的图象,再将此图象向左平移 个单位,
【解析】 函数 的图象上所有点的横坐标伸长到原来的
【答案】 D
的图象,选D.
得
【解析】 由已知得A=3,
所以 故选 B.
【答案】 B
初相是 则这个函数的表达式是( )
的最大值是3,最小正周期
3. 已知函数y=Asin(ox+φ)(A>0,w>0)
事
事
事
4. 函 数 图象的一条对称轴是 . (填序号)
① ;②x=0;③ ;④
【解析】 由正弦函数对称轴可知.
,k∈Z,k=0
【 答案】 ③
k∈Z,
时 ,
5. 已知函数 ,x ∈R.
(1)写出函数 f(x)的对称轴方程、对称中心的坐标及单调区间;
(2)求函数f(x)在区间[0, 上的最大值和最小值.
k∈Z; 由 k∈Z 解得对称中心是 ,k∈Z; 由
解 得 单 调 递 增 区 间 由
解得单调递减区间
,k∈Z,
解 得 f(x)的 对 称 轴 方 程 是
【 解 】 (1)由
(2)∵ ,∴
∴当 即x=0 时 ,f(x) 取最小值为一1;
当 , 即 时 ,f(x) 取最大值为2.
事
课堂小结
1. 知识:如何采用两角和或差的正余弦公式进行合角,借助三角函数的相关性质求值.其中三
角函数最值问题是对三角函数的概念、图像和性质,以及诱导公式、同角三角函数基本关系、 和(差)角公式的综合应用,也是函数思想的具体体现.如何科学的把实际问题转化成数学问题, 如何选择自变量建立数学关系式;求解三角函数在某一区间的最值问题.
2.思想:本节课通过由特殊到一般方式把关系式y=asin x+bcosx化成y=Asin(@x+0)的形式,可
以很好地培养学生探究、归纳、类比的能力.通过探究如何选择自变量建立数学关系式,可
以很好地培养学生分析问题、解决问题的能力和应用意识,进一步培养学生的建模意识.
教材整理1 φ对函数y=sin(x+φ)
时,向_左 平移
y=sinx80 时,向右 平 移φ
的图象的影响
y=sin(x+φ
度
度
长
长
位
位
单
单
个
个
一、[基础·初探]
w>1 时,所有点的横坐标 缩短_到原来
1 y=sin(wx+φ
O
y=sin(x+φ)
纵 坐 标 _伸长_到原来的A 倍
→ y=Asin(wx+
点纵坐标 缩短_到原来的A_倍
教材整理3 A(A>0) 对y=Asin(wx+φ) 的图象的影响
横坐标变为原来的
纵坐标不变
y=Asin
_
1
2.正弦曲线到函数y=Asin(wox+φ) 的图象的变换过程:
的 图 象 纵坐标变为原来的A倍
y=
的图象.
或向右
个单位长度
y=sin x 的图象
向左(
平移
横坐标不变
_的图象
y= S]
振幅
它是做简谐运动的物体离开平衡位置的最大距离
周期
它是物体往复运动_ 一次所需要的时间
频率
它是单位时间内往复运动的 次数
相位 wx+φ
其中_ φ为初相
教材整理4 A,w,φ 的物理意义
在y=Asin(wx+φ),x∈[0, 十 一 ](A>0,w>0) 中,各参数的物理意义.
所有的点向左(φ>0) 或向右(φ<0)平行移动
lφl 个单位长度
横坐标缩短(o>1 )或
伸长(0
纵坐标伸长(A>1 )或 缩短(0
y=sin(x+φ)
y=sinox
y=Asinx
y=sinx
y=sinx
y=sinx
