人教A2019最新版教材高中数学选择性必修第一册2.5.2 圆与圆的位置关系 课件(共30张PPT)
文档属性
| 名称 | 人教A2019最新版教材高中数学选择性必修第一册2.5.2 圆与圆的位置关系 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-06 20:02:57 | ||
图片预览











文档简介
(共30张PPT)
2.5 直线与圆、圆与圆的位置关系
2.5.1 直线与圆的位置关系
素 养 目 标
学 科 素 养
1.掌握直线与圆的三种位置关系:相交、相切、 相离.(重点) 2.会用代数法和几何法来判断直线与圆的三种位 置关系.(难点) 3.会用直线与圆的位置关系解决一些实际问 题.(难点)
1、直观想象 2、数学运算 3、数形结合
学习目标
一 、自主学习
位置关系
交点个数
相交
有2个公共点
相切
只有1个公共点
相离
没有公共点
一.直线与圆的三种位置关系
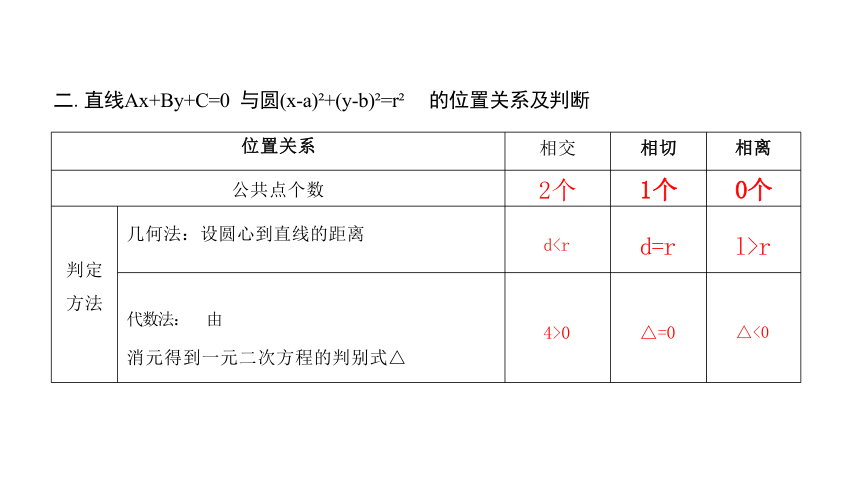
位置关系 相交 相切
相离
公共点个数 2个 1个
0个
判定 方法 几何法:设圆心到直线的距离 dl>r
代数法: 由 消元得到一元二次方程的判别式△ 4>0 △=0
△<0
二.直线Ax+By+C=0 与圆(x-a) +(y-b) =r 的位置关系及判断
小试牛刀
思辨解析(正确的打“ √ ”,错误的打“×”)
(1)若直线与圆有公共点,则直线与圆相交.( × )
(2)如果直线与圆组成的方程组有解,则直线和圆相交或相切.( √ )
(3)若圆心到直线的距离大于半径,则直线与圆的方程联立消元后得到
的一元二次方程无解.( √ )
(4)过不在圆内的一点一定能做两条切线.( × )
二、经典例题
题型一直线与圆的位置关系
例1已知直线方程mx-y—m—1=0, 圆的方程x +y -4x—2y+1=0. m
为何值时,圆与直线:(1)有两个公共点;(2)只有一个公共点;(3)没有公共点.
解:法一:将直线mx-y-m—1=0 代入圆的方程化简整理得,
(1+m )x -2(m +2m+2)x+m +4m+4=0.
∵△=4m(3m+4),
(1)当△>0时,即m>0或 时,直线与圆相交,即直线与圆有两个公共点;
(2)当△=0时,即 m=0 或 时,直线与圆相切,即直线与圆只有一个公共点;
(3)当△<0时,即 时,直线与圆相离,即直线与圆没有公共点.
法二:已知圆的方程可化为(x-2) +(y-1) =4, 即圆心为C(2,1),半 径r=2.
圆心C(2,1)到直线 mx -y—m —1=0 的距离
(1)当d<2时,即m>0或 时,直线与圆相交,即直线与圆有两个公共点;
(2)当d=2 时,即m=0 或 ,直线与圆相切,即直线与圆只有一个公共点;
(3)当d>2时,即 时,直线与圆相离,即直线与圆没有公共点.
总结
直线与圆位置关系判断的三种方法
(1)几何法:由圆心到直线的距离d 与圆的半径r的大小关系判断.
(2)代数法:根据直线与圆的方程组成的方程组解的个数来判断.
(3)直线系法:若直线恒过定点,可通过判断点与圆的位置关系判断,
但有一定的局限性,必须是过定点的直线系.
跟踪训练1
已知直线l:x-2y+5=0 与圆C:(x—7) +(y—1) =36, 判断直线l 与圆C
的位置关系.
解:方法一(代数法)
由方程红 消去y后整理,得5x -50x+61=0.
∵△=(一50) -4×5×61=1280>0,
∴该方程组有两组不同的实数解,即直线l 与 圆C 相交.
方法二(几何法)
圆心(7,1)到直线l 的距离为
∵d题型二圆的切线方程
例2(1)求过圆x +y -2x—4y=0 上一点P(3,3)的切线方程。
(2)求过点P(2,3)且与圆(x—1) +(y-2) =1 相切的直线的方程。
(1)解析 x +y -2x—4y=0 的圆心为C(1,2),
∴切线的斜率k=—2,
∴切线方程为:y-3=-2(x—3), 即2x+y—9=0
.
( 2 ) 求 过 点P(2,3)且与圆(x—1) +(y—2) =1 相切的直线的方程。
解析 P(2,3)在圆(x—1) +(y-2) =1 外,
∴过点P(2,3)与圆(x—1) +(y-2) =1 相切的直线有两条.
当斜率存在时,设切线的斜率为k,
则切线方程为y-3=k(x-2) 即kx-y+3-2k=0,
, ∴k=0,
∴切线方程为y=3,
当斜率不存在时,切线方程为x=2.
∴切线方程为y=3 或x=2.
: ·
总结
1.求过圆上一点(xo,yo) 的圆的切线方程:先求切点与圆心连线的斜率k, 再由垂
直关系得切线的斜率为 由点斜式可得切线方程.如果斜率为零或不存在,
则由图形可直接得切线方程y=yo 或x=xo.
2.求圆外一点(xo,yo) 的圆的切线方程: ①几何法:设切线方程为 y-yo=k(x 一
xo). 由圆心到直线的距离等于半径,可求得k, 也就得切线方程.
②代数法:设切线方程为y-yo=k(x— xo),与圆的方程联立,消去y 后得到关于
x 的一元二次方程,由△=0求出k, 可得切线方程.
提醒:切线的斜率不存在的情况,不要漏解.
则有 则有b=2a,
又由P 在直线l 上,则有一a+2b—3=0, 可解得a=1,b=2,
则直线l 的方程为x+2y-3=0.
则直线l 的方程为
x+2y-3=0 解 析 :根据题意,圆M:x +y + 4x—1=0,
即(x+2) +y =5, 其圆心M(一2,0),
直线l:ax+by-3=0 与圆M:x +y +4x—1=0
跟踪训练2
(1)已知直线l:ax+by-3=0
与 圆M:x +y +4x—1=0 相切于点P(一1,2),
则P 在直线1上且MP 与直线l垂直.
相切于点P(一1,2),
(2)由直线y=x+1 上任一点向圆(x—3) +y =1 引切线,则该切线长的最小
值为( )
A.1 B.2√ C D.3
C 解析:圆心C(3,0)到y=x+1 的距离
所以切线的最小值为
= 8 , 求 直 线l的方程 .
解:(1)联立直线l与 圆C 的方程,
所以交点为A(1,3),B(2,0).
例3(1)求直线l:3x+y-6=0 被圆C:x +y -2y-4=0 截得的弦长|AB|.
(2)过点(一4,0)作直线l 与 圆x +y +2x-4y-20=0 交 于A,B 两点,如果 A|B
故直线l:3x+y-6=0 被 圆C:x +y -2y-4=0 截得的弦长
AB|=√(1-2) +(3-0) =√ 10.
题型三直线与圆相交
解
事 事
事
题型三直线与圆相交
(2)过点(一4,0)作直线l 与圆x +y +2x-4y-20=0 交于A,B两点,如果AB
= 8 , 求 直 线l的方程.
解析:将圆的方程配方得(x+1) +(y-2) =25,
由圆的性质可得,圆心到直线l的距离
①当直线l的斜率不存在时,x=—4 满足题意;
②当直线l 的斜率存在时,设l的方程为y=k(x+4), 即 kx-y+4k=0.
由点到直线的距离公式,得
解得 所以直线l的方程为5x+12y+20=0.
综上所述,直线l 的方程为x+4=0 或 5x+12 y+20=0.
求直线与圆相交时的弦长有三种方法
1.交点法:将直线方程与圆的方程联立,求出交点A,B 的坐标,根据两点间的距离公
式 |AB|=√(x -x ) +(y -y ) 求解.
2.弦长公式:
如图所示,将直线方程与圆的方程联立,设直线与圆的两交点分别是
A(xi,yi),B(x ,y2), 则AB|=√(x -x ) +(v -y ) =√ 1+k |x -x l
直线l 的斜率k 存在且不为0).
3.几何法:如图,直线与圆C 交于A,B 两点,设弦心距为d, 圆的半径为r, 弦长为
AB|, 则有 即AB|=2√ r -d .通常采用几何法较为简便.
总结
跟踪训练3
圆心为C(2, 一1),截直线y=x—1的弦长为2√2的圆的方程为
(x-2) +(y+1) =4
解析:设圆的半径为r, 由条件,得圆心到直线y=x—1 的距离为
又直线y=x-1 被圆截得的弦长为2 √2,即半弦长为 √2,
∴r =2+2=4, 得 r=2,
∴所求圆的方程为(x—2) +(y+1) =4.
三、当堂达标
1.直线y=x+1 与 圆x +y =1 的位置关系是( )
A. 相切 B.相交但直线不过圆心
C.直线过圆心 D.相离
B 解析:∵圆心(0,0)到直线y=x+1 的距离
∴直线与圆x +y =1 相交,
又(0,0)不在y=x+1 上,∴直线不过圆心.
2.直线m:x+y-1=0 被圆M:x +y -2x—4y=0 截得的弦长为( )
A.4 B.2√3 C. D.
B 解析:∵x +y -2x—4y=0,∴(x—1) +(y-2) =5,
∴圆M的圆心坐标为(1,2),半径为√5,又点(1,2)到直线x+y-1=0 的距离
直 线m 被 圆M 截得的弦长等于2 √ ( √5) -( √2) =2 √3.
3.(多选)已知直线l:kx-y+2k=0 和圆0:x +y =16, 则 ( )
A.直线l恒过定点(2,0)
B. 存在k 使得直线l 与直线l :x-2y+2=0 垂直
C.直线l 与圆O 相交
D. 若k=-1, 直 线l 被 圆O 截得的弦长为4
BC
解析:对于 A、C, 由 l:kx-y+2k=0, 得k(x+2)-y=0, 直 线l恒过定点(-2,0),故A 错误;
因为直线1恒过定点(-2,0),而(-2) +O =4<16, 即(-2,0)在圆O:x +y =16 内,故C 正确;
对于B, 直线l 。:x-2y+2=0 的斜率为 , 则 当k=-2 时,满足直线1与直线l 。:x-2y+2=0 垂直,
故 B 正确;
对于D,k=-1 时,直线l:x+y+2=0, 圆心到直线的距离为
所以直线l 被圆O 截得的弦长为2√ -d =2\4 -(√2) =2√ 14, 故 D 错误.
4.已知直线l:(2m+1)x+(m+1)y=7m+4, 圆 C:(x—1) +(y-2) =25,
则直线l与圆C 的位置关系为
相交解析:由直线方程得(2x+y-7)m+x+y-4=0,
故直线l 过定点A(3,1).
由A|C|=√(3-1) +(1-2) =√5<5 得A点在圆内,
因此直线l与圆C 相交.
5.若点P(1,2)在以坐标原点为圆心的圆上,则该圆在点P 处的切线方
程为
x+2y-5=0 解 析 :由题意,得 则该圆在点P 处的切线
的斜率为 所以所求切线方程为 即x+2y-5=0.
6.已知圆C 经过点A(2,0),B(1, 一 √3),且圆心C 在直线y=x 上.
(1)求圆C的方程;
(2)过 的直线l 截圆所得弦长为2√3,求直线l 的方程.
解:(1)AB的中点坐标 的斜率为 √3.可得AB垂直平分线方
程为2 √3x+6y=0, 与x—y=0的交点为(0,0),圆心坐标(0,0),半径为2,
所以圆C 的方程为x +y =4.
(2)直线的斜率存在时,设直线的斜率为k, 又 直 线l
∴直线l 的方程为
则圆心(0,0)到直线的距离 又圆的半径r=2, 截得的弦长为2√3, 则有 则直线l 的方程为
当直线的斜率不存在时,直线方程为x=1, 满足题意 .
∴直线l 的方程为x=1 或
对应课后练习
课后作业
2.5 直线与圆、圆与圆的位置关系
2.5.1 直线与圆的位置关系
素 养 目 标
学 科 素 养
1.掌握直线与圆的三种位置关系:相交、相切、 相离.(重点) 2.会用代数法和几何法来判断直线与圆的三种位 置关系.(难点) 3.会用直线与圆的位置关系解决一些实际问 题.(难点)
1、直观想象 2、数学运算 3、数形结合
学习目标
一 、自主学习
位置关系
交点个数
相交
有2个公共点
相切
只有1个公共点
相离
没有公共点
一.直线与圆的三种位置关系
位置关系 相交 相切
相离
公共点个数 2个 1个
0个
判定 方法 几何法:设圆心到直线的距离 d
代数法: 由 消元得到一元二次方程的判别式△ 4>0 △=0
△<0
二.直线Ax+By+C=0 与圆(x-a) +(y-b) =r 的位置关系及判断
小试牛刀
思辨解析(正确的打“ √ ”,错误的打“×”)
(1)若直线与圆有公共点,则直线与圆相交.( × )
(2)如果直线与圆组成的方程组有解,则直线和圆相交或相切.( √ )
(3)若圆心到直线的距离大于半径,则直线与圆的方程联立消元后得到
的一元二次方程无解.( √ )
(4)过不在圆内的一点一定能做两条切线.( × )
二、经典例题
题型一直线与圆的位置关系
例1已知直线方程mx-y—m—1=0, 圆的方程x +y -4x—2y+1=0. m
为何值时,圆与直线:(1)有两个公共点;(2)只有一个公共点;(3)没有公共点.
解:法一:将直线mx-y-m—1=0 代入圆的方程化简整理得,
(1+m )x -2(m +2m+2)x+m +4m+4=0.
∵△=4m(3m+4),
(1)当△>0时,即m>0或 时,直线与圆相交,即直线与圆有两个公共点;
(2)当△=0时,即 m=0 或 时,直线与圆相切,即直线与圆只有一个公共点;
(3)当△<0时,即 时,直线与圆相离,即直线与圆没有公共点.
法二:已知圆的方程可化为(x-2) +(y-1) =4, 即圆心为C(2,1),半 径r=2.
圆心C(2,1)到直线 mx -y—m —1=0 的距离
(1)当d<2时,即m>0或 时,直线与圆相交,即直线与圆有两个公共点;
(2)当d=2 时,即m=0 或 ,直线与圆相切,即直线与圆只有一个公共点;
(3)当d>2时,即 时,直线与圆相离,即直线与圆没有公共点.
总结
直线与圆位置关系判断的三种方法
(1)几何法:由圆心到直线的距离d 与圆的半径r的大小关系判断.
(2)代数法:根据直线与圆的方程组成的方程组解的个数来判断.
(3)直线系法:若直线恒过定点,可通过判断点与圆的位置关系判断,
但有一定的局限性,必须是过定点的直线系.
跟踪训练1
已知直线l:x-2y+5=0 与圆C:(x—7) +(y—1) =36, 判断直线l 与圆C
的位置关系.
解:方法一(代数法)
由方程红 消去y后整理,得5x -50x+61=0.
∵△=(一50) -4×5×61=1280>0,
∴该方程组有两组不同的实数解,即直线l 与 圆C 相交.
方法二(几何法)
圆心(7,1)到直线l 的距离为
∵d
例2(1)求过圆x +y -2x—4y=0 上一点P(3,3)的切线方程。
(2)求过点P(2,3)且与圆(x—1) +(y-2) =1 相切的直线的方程。
(1)解析 x +y -2x—4y=0 的圆心为C(1,2),
∴切线的斜率k=—2,
∴切线方程为:y-3=-2(x—3), 即2x+y—9=0
.
( 2 ) 求 过 点P(2,3)且与圆(x—1) +(y—2) =1 相切的直线的方程。
解析 P(2,3)在圆(x—1) +(y-2) =1 外,
∴过点P(2,3)与圆(x—1) +(y-2) =1 相切的直线有两条.
当斜率存在时,设切线的斜率为k,
则切线方程为y-3=k(x-2) 即kx-y+3-2k=0,
, ∴k=0,
∴切线方程为y=3,
当斜率不存在时,切线方程为x=2.
∴切线方程为y=3 或x=2.
: ·
总结
1.求过圆上一点(xo,yo) 的圆的切线方程:先求切点与圆心连线的斜率k, 再由垂
直关系得切线的斜率为 由点斜式可得切线方程.如果斜率为零或不存在,
则由图形可直接得切线方程y=yo 或x=xo.
2.求圆外一点(xo,yo) 的圆的切线方程: ①几何法:设切线方程为 y-yo=k(x 一
xo). 由圆心到直线的距离等于半径,可求得k, 也就得切线方程.
②代数法:设切线方程为y-yo=k(x— xo),与圆的方程联立,消去y 后得到关于
x 的一元二次方程,由△=0求出k, 可得切线方程.
提醒:切线的斜率不存在的情况,不要漏解.
则有 则有b=2a,
又由P 在直线l 上,则有一a+2b—3=0, 可解得a=1,b=2,
则直线l 的方程为x+2y-3=0.
则直线l 的方程为
x+2y-3=0 解 析 :根据题意,圆M:x +y + 4x—1=0,
即(x+2) +y =5, 其圆心M(一2,0),
直线l:ax+by-3=0 与圆M:x +y +4x—1=0
跟踪训练2
(1)已知直线l:ax+by-3=0
与 圆M:x +y +4x—1=0 相切于点P(一1,2),
则P 在直线1上且MP 与直线l垂直.
相切于点P(一1,2),
(2)由直线y=x+1 上任一点向圆(x—3) +y =1 引切线,则该切线长的最小
值为( )
A.1 B.2√ C D.3
C 解析:圆心C(3,0)到y=x+1 的距离
所以切线的最小值为
= 8 , 求 直 线l的方程 .
解:(1)联立直线l与 圆C 的方程,
所以交点为A(1,3),B(2,0).
例3(1)求直线l:3x+y-6=0 被圆C:x +y -2y-4=0 截得的弦长|AB|.
(2)过点(一4,0)作直线l 与 圆x +y +2x-4y-20=0 交 于A,B 两点,如果 A|B
故直线l:3x+y-6=0 被 圆C:x +y -2y-4=0 截得的弦长
AB|=√(1-2) +(3-0) =√ 10.
题型三直线与圆相交
解
事 事
事
题型三直线与圆相交
(2)过点(一4,0)作直线l 与圆x +y +2x-4y-20=0 交于A,B两点,如果AB
= 8 , 求 直 线l的方程.
解析:将圆的方程配方得(x+1) +(y-2) =25,
由圆的性质可得,圆心到直线l的距离
①当直线l的斜率不存在时,x=—4 满足题意;
②当直线l 的斜率存在时,设l的方程为y=k(x+4), 即 kx-y+4k=0.
由点到直线的距离公式,得
解得 所以直线l的方程为5x+12y+20=0.
综上所述,直线l 的方程为x+4=0 或 5x+12 y+20=0.
求直线与圆相交时的弦长有三种方法
1.交点法:将直线方程与圆的方程联立,求出交点A,B 的坐标,根据两点间的距离公
式 |AB|=√(x -x ) +(y -y ) 求解.
2.弦长公式:
如图所示,将直线方程与圆的方程联立,设直线与圆的两交点分别是
A(xi,yi),B(x ,y2), 则AB|=√(x -x ) +(v -y ) =√ 1+k |x -x l
直线l 的斜率k 存在且不为0).
3.几何法:如图,直线与圆C 交于A,B 两点,设弦心距为d, 圆的半径为r, 弦长为
AB|, 则有 即AB|=2√ r -d .通常采用几何法较为简便.
总结
跟踪训练3
圆心为C(2, 一1),截直线y=x—1的弦长为2√2的圆的方程为
(x-2) +(y+1) =4
解析:设圆的半径为r, 由条件,得圆心到直线y=x—1 的距离为
又直线y=x-1 被圆截得的弦长为2 √2,即半弦长为 √2,
∴r =2+2=4, 得 r=2,
∴所求圆的方程为(x—2) +(y+1) =4.
三、当堂达标
1.直线y=x+1 与 圆x +y =1 的位置关系是( )
A. 相切 B.相交但直线不过圆心
C.直线过圆心 D.相离
B 解析:∵圆心(0,0)到直线y=x+1 的距离
∴直线与圆x +y =1 相交,
又(0,0)不在y=x+1 上,∴直线不过圆心.
2.直线m:x+y-1=0 被圆M:x +y -2x—4y=0 截得的弦长为( )
A.4 B.2√3 C. D.
B 解析:∵x +y -2x—4y=0,∴(x—1) +(y-2) =5,
∴圆M的圆心坐标为(1,2),半径为√5,又点(1,2)到直线x+y-1=0 的距离
直 线m 被 圆M 截得的弦长等于2 √ ( √5) -( √2) =2 √3.
3.(多选)已知直线l:kx-y+2k=0 和圆0:x +y =16, 则 ( )
A.直线l恒过定点(2,0)
B. 存在k 使得直线l 与直线l :x-2y+2=0 垂直
C.直线l 与圆O 相交
D. 若k=-1, 直 线l 被 圆O 截得的弦长为4
BC
解析:对于 A、C, 由 l:kx-y+2k=0, 得k(x+2)-y=0, 直 线l恒过定点(-2,0),故A 错误;
因为直线1恒过定点(-2,0),而(-2) +O =4<16, 即(-2,0)在圆O:x +y =16 内,故C 正确;
对于B, 直线l 。:x-2y+2=0 的斜率为 , 则 当k=-2 时,满足直线1与直线l 。:x-2y+2=0 垂直,
故 B 正确;
对于D,k=-1 时,直线l:x+y+2=0, 圆心到直线的距离为
所以直线l 被圆O 截得的弦长为2√ -d =2\4 -(√2) =2√ 14, 故 D 错误.
4.已知直线l:(2m+1)x+(m+1)y=7m+4, 圆 C:(x—1) +(y-2) =25,
则直线l与圆C 的位置关系为
相交解析:由直线方程得(2x+y-7)m+x+y-4=0,
故直线l 过定点A(3,1).
由A|C|=√(3-1) +(1-2) =√5<5 得A点在圆内,
因此直线l与圆C 相交.
5.若点P(1,2)在以坐标原点为圆心的圆上,则该圆在点P 处的切线方
程为
x+2y-5=0 解 析 :由题意,得 则该圆在点P 处的切线
的斜率为 所以所求切线方程为 即x+2y-5=0.
6.已知圆C 经过点A(2,0),B(1, 一 √3),且圆心C 在直线y=x 上.
(1)求圆C的方程;
(2)过 的直线l 截圆所得弦长为2√3,求直线l 的方程.
解:(1)AB的中点坐标 的斜率为 √3.可得AB垂直平分线方
程为2 √3x+6y=0, 与x—y=0的交点为(0,0),圆心坐标(0,0),半径为2,
所以圆C 的方程为x +y =4.
(2)直线的斜率存在时,设直线的斜率为k, 又 直 线l
∴直线l 的方程为
则圆心(0,0)到直线的距离 又圆的半径r=2, 截得的弦长为2√3, 则有 则直线l 的方程为
当直线的斜率不存在时,直线方程为x=1, 满足题意 .
∴直线l 的方程为x=1 或
对应课后练习
课后作业
