人教A版(2019)高中数学必修第二册教学课件:第八章 8.1 基本立体图形 (共52张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学必修第二册教学课件:第八章 8.1 基本立体图形 (共52张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-06 20:03:10 | ||
图片预览











文档简介
(共52张PPT)
第八章立体几何初步 8.1 基本立体图形
学习目标
1.认识柱、锥、台、球及简单组合体的结构特征.
2.能运用结构特征描述现实生活中简单物体的结构..
重点:感受大量空间实物及模型,概括出柱、锥、台、球的结构
特征.
难点:柱、锥、台、球的结构特征的概括.
知识梳理
一 、 空间几何体、多面体与旋转体
1.空间几何体
空间中的物体,都占据着空间的一部分.如果只考虑这些物体的形
状和大小,而不考虑其他因素,那么由这些物体抽象出来的空间图 形就叫做空间几何体.
2.多面体
(1)定义:由若干个平面多边形围成的几何体叫做多面 体 .
(2)组成元素:围成多面体的各个多边形叫做多面体的
面;两个面的公共边叫做多面体的棱,棱与棱的公共点叫 做多面体的顶点,
3.旋转体
一条平面曲线(包括直线)绕它所在平面内的一条定直线
旋转所形成的曲面叫做旋转面,封闭的旋转面围成的几何 体叫做旋转体.这条定直线叫做旋转体的轴.
归纳提升
1.多面体是由平面多边形围成的,这里的多边形包括它内
部的平面部分.
2.多面体至少有四个面,如图所示的多面体即是四个面的
情况 .
3.一个多面体由几个面围成就称为几面体.如四面体、五
面体、六面体....
特别提醒
1.旋转体是由“平面图形”旋转而形成的,这个平面图形可以是矩形、
三角形或其他图形.
2.平面图形绕定直线旋转形成旋转体,这条定直线可以是平面图形的
边所在的直线,也可以不是,但定直线一定与平面图形在同一个平面 内 .
3.与多面体一样,旋转体是封闭的几何体,包括表面及其内部所有的
点 .
特别提醒
1.旋转体是由“平面图形”旋转而形成的,这个平面图形可以是矩形、
三角形或其他图形.
2.平面图形绕定直线旋转形成旋转体,这条定直线可以是平面图形的
边所在的直线,也可以不是,但定直线一定与平面图形在同一个平面 内 .
3.与多面体一样,旋转体是封闭的几何体,包括表面及其内部所有的
点 .
二、棱柱、棱锥、棱台
1.棱柱
( 1 ) 定 义 :如图8-1-1,有两个面互相平行,其余各面都 是四边形,并且相邻两个四边形的公共边都互相平行,由这 些面所围成的多面体叫做棱柱.在棱柱中,两个互相平行的面 叫做棱柱的底面,它们是全等的多边形;其余各面叫做棱柱 的侧面,它们都是平行四边形;相邻侧面的公共边叫做棱柱 的侧棱;侧面与底面的公共顶点叫做棱柱的顶点.
图8-1-1
C
>底面
顶点
侧面
侧被 — —
Fk
E-
(2)记法:棱柱用表示底面各顶点的字母来表示,如图
8.1-1中的棱柱记作棱柱ABCDEF-A'B'C'D'E'F'.
(3)分类:按底面多边形分类.
棱柱的底面可以是三角形、四边形、五边形.…,我们把
这样的棱柱分别叫做三棱柱、四棱柱、五棱柱 ….
按侧棱与底面是否垂直分类.
一般地,我们把侧棱垂直于底面的棱柱叫做直棱柱,侧棱
不垂直于底面的棱柱叫做斜棱柱.底面是正多边形的直棱柱 叫做正棱柱.底面是平行四边形的四棱柱也叫做平行六面体
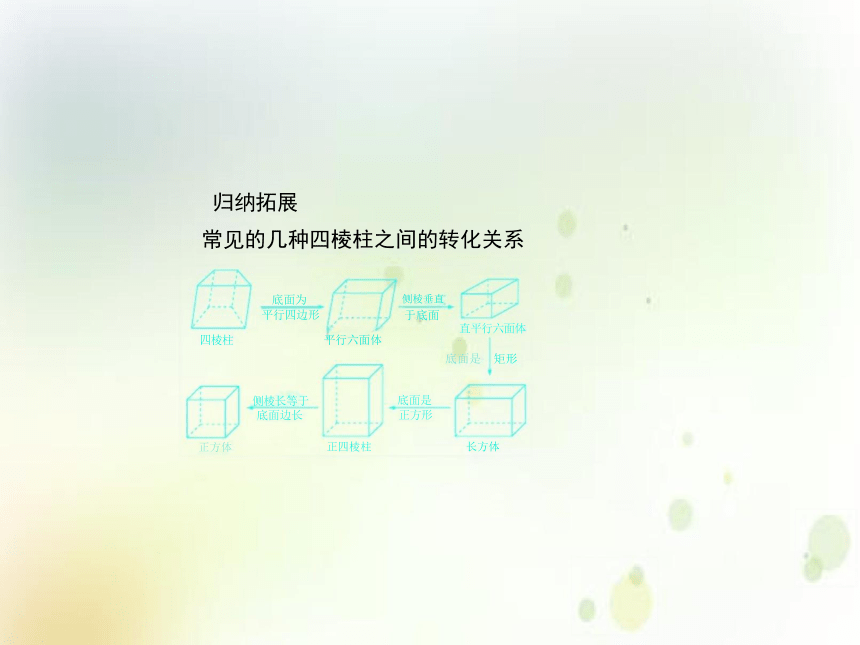
归纳拓展
常见的几种四棱柱之间的转化关系
侧棱垂直
于底面
平行六面体
底面为
平行四边形
四棱柱
正方体 正四棱柱 长方体
直平行六面体
底面是 矩形
侧棱长等于 底面边长
底面是 正方形
2.棱锥
( 1 ) 定 义 :如图8-1-2,一般地,有一个面是多边
形,其余各面都是有一个公共顶点的三角形,由这些
面所围成的多面体叫做棱锥.这个多边形面叫做棱锥
的底面;有公共顶点的各个三角形面叫做棱锥的侧面;
相邻侧面的公共边叫做棱锥的侧棱;各侧面的公共顶
点叫做棱锥的顶点.
图8-1-2
(2)表示:棱锥用表示顶点和底面各顶点的字母来表示,
如图8-1-2中的棱锥记作棱锥S-ABCD.
(3)分类:棱锥的底面可以是三角形、四边形、五边
形...,我们把这样的棱锥分别叫做三棱锥、四棱锥、五棱
锥 … . . . ,其中三棱锥又叫四面体 . 底面是正多边形,并且顶
点与底面中心的连线垂直于底面的棱锥叫做正棱锥.
归纳拓展
正棱锥的相关概念及性质:
(1)正棱锥的斜高
正棱锥侧面的等腰三角形底边上的高叫做正棱锥的斜高.正棱
锥的斜高都相等.
(2)正棱锥的简单性质
各侧棱相等,各侧面都是全等的等腰三角形,斜高都相等.
正棱锥的高、斜高和斜高在底面上的射影组成一个直角三角 形;正棱锥的高、侧棱和侧棱在底面上的射影也组成一个直 角三角形.
3.棱台
(1)定义:如图8-1-3,用一个平行于棱锥底面的平面去 截棱锥,我们把底面和截面之间那部分多面体叫做棱台.在棱 台中,原棱锥的底面和截面分别叫做棱台的下底面和上底面. 类似于棱柱、棱锥,棱台也有侧面、侧棱、顶点.
图8-1-3
( 2 ) 记 法 :棱台用表示底面各顶点的字母来表示,如图
8.1-3中的棱台记作棱台ABCD-A'B'C'D'.
( 3 ) 分 类 :由三棱锥、四棱锥、五棱锥...截得的棱台分
别叫做三棱台、四棱台、五棱台...
归纳提升
棱台是用平行于棱锥底面的平面去截棱锥,底面
与截面之间的部分,这是从棱锥出发去定义棱台. 它说明了棱台与棱锥的联系,为我们提供了解决 棱台问题的一种方法,棱台问题常常转化为棱锥 问题来解决,即还台为锥.
小结&拓展
棱柱、棱锥、棱台都是多面体,它们相互之间没有公共部分;四面
体是一种特殊的棱锥(三棱锥);直棱柱和平行六面体都是棱柱, 它们又有公共部分——直平行六面体,而长方体是特殊的直平行六 面体.
1.所有棱长都相等的三棱锥叫做正四面体.
2.正三棱锥与正四面体的区别和联系
正四面体各个面都是全等的等边三角形.正四面体是正三棱锥,但正
三棱锥只有在侧棱与底面三角形边长相等时才是正四面体.
圆柱
图形及表示
定义:以矩形的一边所在直线为旋转轴,其余三边旋转形成的面 所围成的旋转体叫做圆柱
相关概念: 圆柱的轴:旋转轴.圆柱的底面:垂直于轴的边旋转而成的圆面 圆柱的侧面:平行于轴的边旋转而成的曲面. 圆柱侧面的母线:无论旋转到什么位置,不垂直于轴的边.
图中圆柱表示
为:圆柱00
轴
底面
侧面 母线
A
底面
A'
0
0
三、圆柱、圆锥、圆台和球
.
圆锥
图形及表示
定义:以直角三角形的一条直角边所在直线为为旋转轴 其余两边旋转形成的面所围成的旋转体
侧
母线
底
图中圆锥表示为圆锥SO
相关概念: 圆锥的轴:旋转轴 圆锥的底面:垂直于轴的边旋转而成的圆面 侧面:直角三角形的斜边旋转而成的曲面 母线:无论旋转到什么位置,不垂直于轴的边
圆台 图形及表示
定义:用平行于圆锥底面的平面去截圆锥,底面与截面之间的部分叫 做圆台 旋转法定义:以直角梯形中垂直于底边的腰所在直线为旋转轴,将直 角梯形绕旋转轴旋转一周而形成的旋转体叫做圆台 底面 侧 面 、 母线 底面
轴
相关概念: 圆台的轴:旋转轴 圆台的底面:垂直于轴的边旋转一周所形成的圆面 圆台的侧面:不垂直于轴的边旋转一周所形成的曲面 母线:无论旋转到什么位置,不垂直于轴的边
图中圆台表示为:圆台 O'0
球
图形及表示
定义:半圆以它的直径所在直线为旋转轴,旋转一周形 成的曲面叫做球面(是“空 心 ”的),球面所围成的旋 转体叫做球体,简称球(是“实 心 ”的) .
半径
0
直径
相关概念: 球心:半圆的圆心 半径:连接球心和球面上任意一点的线段叫做球的半径 直径:连接球面上两点并且经过球心的线段叫做球的直 径(即半圆的直径).
图中的球表示为:球O
球心
相同点 不同点
联系
棱柱 、棱 锥 、 棱台 都由平面多边 形围成,都有 底面,且底面 都是多边形 棱柱两个底面,平行且全 等;棱锥一个底面;棱台 两个底面,平行且相似
棱台是由 棱锥截取 得到的
圆柱 、圆 锥 、 圆台 都由平面多边 形旋转形成, 都有底面,且 底面都是圆面 圆柱两个底面,是半径相 等的圆面;圆锥一个底面 ,是圆面;圆台两个底面 ,是不全等但相似的圆面
圆台是由 圆锥截取 得到的
空间几何体在结构上的相同点和不同点及联系
柱体 上底扩大 台体 上底缩小 锥体
四 . 简单组合体
(1)定义:由简单几何体组合而成的几何体
称作简单组合体.
(2)构成形式:
①由简单几何体拼接而成.
②由简单几何体截去或挖去一部分而成.
常考题型
一 . 空间几何体概念的理解
<1>柱、锥、台、球的结构特征
例1.下列说法正确的是 ( )
A.各个面都是三角形的几何体是三棱锥
B.多面体至少有三个面
C.各侧面都是正方形的四棱柱一定是正方体
D.九棱柱有9条侧棱,9个侧面,侧面为平行四边形
【解析】 选 项A 错,反例如图8-1-4;一个多面体至少有四
个面,如三棱锥有四个面,不存在只有三个面的多面体,所 以选项B错;选项C错,上、下底面是全等的菱形,各侧面是 全等的正方形,它不是正方体;根据棱柱的定义,知选项D 正确.
图8-1-4
【答案】 D
训练题1
1下列三个命题中,正确的有( )
①棱柱中互相平行的两个面叫做棱柱的底面;②有两
个面互相平行,其余四个面都是等腰梯形的六面体是 棱台;③四棱锥有4个顶点.
A.0个 B.1 个 C.2 个 D.3 个
1.A 解析:①错误,底面为正六边形的棱柱相对的两
个侧面互相平行,但不能作为底面.②错误,因为不能 保证侧棱相交于同一点.③错误,四棱锥只有一个顶点, 就是各侧面的公共顶点.
训练题2
下列叙述中正确的个数是 ( )
①以直角三角形的一边所在直线为轴旋转所得的旋转体
是圆锥;
②以直角梯形的一腰所在直线为轴旋转所得的旋转体是
圆台;
③半圆绕其直径所在的直线旋转一周所形成的曲面是球;
④用一个平面去截圆锥,得到一个圆锥和一个圆台.
A.0 B.1 C.2 D.3
2.A 解析:①错误,应以直角三角形的一条直角边所在直线
为轴;(2)错误,应以直角梯形的垂直于底边的腰所在直线为轴;
③错误,应把“球”改成“球面”;④错误,应是用一个与底 面平行的平面去截圆锥.
训练题3
下列说法:(1)圆柱的底面是圆面;(2)经过圆柱任意两条母线的截面
是一个矩形面;(3)圆台的任意两条母线的延长线,可能相交,也可能不 相交;(4)夹在圆柱的两个截面间的几何体还是一个旋转体.其中正确的 是
3 . (1)(2)解析:(1)正确,圆柱的底面是圆面;(2)正确,经过
圆柱任意两条母线的截面是一个矩形面;(3)不正确,圆台的母线延长 后相交于一点;(4)不正确,夹在圆柱的两个平行于底面的截面间的几 何体才是旋转体.
特别提示:(1)对多面体的判断, 一定要紧扣棱柱、棱锥、棱
台的结构特征,注意概念中的特殊字眼,切不可马虎大意,如 棱柱的概念中的“相邻”,棱锥的概念中的“公共顶点”,棱 台的概念中的“棱锥”等.
(2)圆柱、圆锥、圆台和球都是由一个平面图形绕其特定边(直
径)所在的直线旋转而成的几何体,必须准确认识各旋转体对 旋转轴的具体要求.只有理解了各旋转体的形成过程,才能明确 由此产生的母线、轴、底面等概念,进而判断与这些概念有关 的命题的真假.
(1) (2) (3)
图8-1-5
【解题提示】结合简单组合体的两种基本构成形式入手分析.
【解】 图8-1-5(1)所示的几何体是由两个圆台拼接而成
的组合体;图8-1-5(2)所示的几何体是由一个圆台挖去一 个圆锥得到的组合体;图8-1-5(3)所示的几何体是在一个 圆柱中间挖去一个三棱柱后得到的组合体.
<2>简单组合体的结构特征
例2.描述下列几何体的结构特征.
训练题4[2019·湖南长沙雨花区检测]如图8-1-6(1)(2)
所示,绕虚线旋转一周后形成的旋转体是由哪些简单几何体
(1) (2)
图8-1-6
组成的
4.解:如图D-8-1所示,其中图(1)是由一个圆柱O O
和圆台O O 、 圆 台O O 组成的;图(2)是由一个圆锥 O O 、 一个圆柱O O 及一个圆台O O 中挖去圆锥O O 组成的.
(1) (2)
图D-8-1
判断实物是由哪些简单几何体组成的技巧
(1)准确理解简单几何体(柱、锥、台、球)的结构特征.
(2)正确掌握简单组合体构成的两种基本形式.
(3)若用分割的方法,则需要根据几何体的结构特征恰当地作
出辅助线(或面) .
二 . 空间几何体的侧面展开图
例3.如图8-1-7所示,在以O为顶点的三棱锥中,过O的三
条棱两两的交角都是30°,在一条棱上有A,B 两 点 ,OA=4,
OB=3 ,以A ,B为端点用一条绳子紧绕三棱锥的侧面一周(绳
和侧面无摩擦),求此绳在A,B 之间的最短绳长.
图8-1-7
图8-1-8
A,B 两点间的最短绳长就是线段AB的长度.因为OA=4,
OB=3,∠AOB=90°, 所以AB=5, 即此绳在A,B 之间的
最短绳长为5.
【解】 作出三棱锥的侧面展开图,如图8-1-8.
【解题提示】
把点A,B 所在侧棱剪开, 再将三棱锥侧面展开
利用平面几何 知识求解问题
训练题5[2019·安徽合肥高一检测]如图8-1-9,圆锥的底
面半径为r, 母线长为4r, 一细绳从A点开始,绕圆锥侧面一 圈又回到A点,试求细绳的最短长度.
图8-1-9
图D-8-2
∵圆锥的底面半径为r,
∴I=2πr.∵ 以母线长4r为半径的圆的周长为I=8πr,
. , ∴∠ASA'=90° .
∴AA'=4 √2 r..:.细绳的最短长度为4 √2r.
5.解:把圆锥的侧面沿SA剪开并展开在平面内得一扇形,
如图D-8-2, 则细绳的最短长度即线段AA'的长度.
求空间几何体表面上两点间的最短距离问题的常用方法
求空间几何体表面上两点间的最短距离问题,常常要归结为
求平面上两点间的最短距离问题,因此解决这类问题的方法 就是先把空间几何体的侧面展开成平面图形,再用平面几何 的知识来求解.
训练题6.[2019·陕西西安未央区期末]某人用如图8-1-10
所示的纸片,沿折痕折后粘成一个四棱锥形的“走马灯”
正方形做灯底,且有一个三角形面上写上了“年”字,当灯
旋转时,正好看到“新年快乐”的字样,则在①②③处应依 次 写 上 ( )
图8-1-10
A.快、新、乐 B.乐、新、快 C.新、乐、快 D.乐、快、新
6.A 解析:根据四棱锥图形,正好看到“新年快乐”
的字样时选项A 正确.
【名师点拨】
解答展开与折叠问题,要结合空间几何体的定义和结
构特征,发挥空间想象能力.必要时可制作侧面展开图 进行实践操作.
① ② ③
图8-1-11
则原几何体应为:
① ,②_ ,③_
____
训练题7.如图8-1-11是三个几何体的平面展开图,
7.五棱柱五棱锥三棱台解析:各展开图对应的几何
故①是五棱柱,②是五棱锥,③是三棱台.
①
图D-8-3
体如图D-8-3 所示.
②
③
三 . 空间几何体的轴截面及计算问题
例4.一个圆锥的底面半径为2 cm, 高为6 cm,
在圆锥内部有一个高为x cm的内接圆柱.
( 1 ) 用x表示圆柱的轴截面面积S.
( 2 ) 当x为何值时,S 最大
(1)设圆柱的底面半径为r cm,
f
∴当x=3时,S取得最大值,Smax=6 cm .
【解】
则由
训练题8.
[2019·江苏泰州姜堰区检测]圆台上底面面积为π,下底面面积为
16π,用一个平行于底面的平面去截圆台,该平面自上而下分圆台的 高的比为2:1,求这个截面的面积.
图D-8-4
过点D作DF⊥AB于点F, 交GH于点E.由题意知DO =1,
AO =4,∴AF=3.
∵DE=2EF,∴DF=3EF,∴ , ∴GE=2.
∴圆O 的半径为3,∴这个截面的面积为9π.
8.解:圆台的轴截面如图D-8-4所示,O ,O ,O
为上底面、下底面、截面的圆心.
分别
【名师点拨】
1.圆锥的轴截面是以2r(r为圆锥的底面半径)为底边,I(I为
圆锥的母线长)为腰的等腰三角形.
2.圆柱的轴截面是以2r(r为圆柱的底面半径)和I(I 为圆柱的
母线长)为相邻两边的矩形.
3.圆台的轴截面是以2r ,2r 为 底 ,I(I 为圆台的母线长)为
腰的等腰梯形.
四易错易混问题
<1>对棱柱、棱锥、棱台的概念理解不到位致误
例5.如图8-1-12,甲、乙、丙分别是棱柱、棱锥、棱台吗
图8-1-12
为什么
丙
甲
乙
【解】 图甲不是棱柱,因为虽然上、下两个面平行,但是
四边形ABB A 与四边形A B B A 不在一个平面内,所以多
边形ABB B A A 不是一个平面图形,它更不是一个平行四
边形,所以这个几何体不是棱柱;图乙不是棱锥,因为它的
六个三角形没有一个公共点,故不是棱锥,只是一个多面体;
图丙不是棱台,因为其侧棱的延长线不能相交于同一点.
【防错有术】
切实理解棱柱、棱锥和棱台的定义是解答此类问题 的关键 .
<2>画错截面图致错
例6.在底面半径为3,高为6的圆锥内有一个内接正方体,
求内接正方体的棱长.
则OO'=6,O'M=3,AA'=a,AC'=√2a,:
解得a=6 √2-6.
∴内接正方体的棱长为6 √2-6.
【解】 设正方体的棱长为a, 此空间几何体的示意图如图
8-1-13,作轴截面如图8-1-14,
图8-1-14
图8-1-13
,
第八章立体几何初步 8.1 基本立体图形
学习目标
1.认识柱、锥、台、球及简单组合体的结构特征.
2.能运用结构特征描述现实生活中简单物体的结构..
重点:感受大量空间实物及模型,概括出柱、锥、台、球的结构
特征.
难点:柱、锥、台、球的结构特征的概括.
知识梳理
一 、 空间几何体、多面体与旋转体
1.空间几何体
空间中的物体,都占据着空间的一部分.如果只考虑这些物体的形
状和大小,而不考虑其他因素,那么由这些物体抽象出来的空间图 形就叫做空间几何体.
2.多面体
(1)定义:由若干个平面多边形围成的几何体叫做多面 体 .
(2)组成元素:围成多面体的各个多边形叫做多面体的
面;两个面的公共边叫做多面体的棱,棱与棱的公共点叫 做多面体的顶点,
3.旋转体
一条平面曲线(包括直线)绕它所在平面内的一条定直线
旋转所形成的曲面叫做旋转面,封闭的旋转面围成的几何 体叫做旋转体.这条定直线叫做旋转体的轴.
归纳提升
1.多面体是由平面多边形围成的,这里的多边形包括它内
部的平面部分.
2.多面体至少有四个面,如图所示的多面体即是四个面的
情况 .
3.一个多面体由几个面围成就称为几面体.如四面体、五
面体、六面体....
特别提醒
1.旋转体是由“平面图形”旋转而形成的,这个平面图形可以是矩形、
三角形或其他图形.
2.平面图形绕定直线旋转形成旋转体,这条定直线可以是平面图形的
边所在的直线,也可以不是,但定直线一定与平面图形在同一个平面 内 .
3.与多面体一样,旋转体是封闭的几何体,包括表面及其内部所有的
点 .
特别提醒
1.旋转体是由“平面图形”旋转而形成的,这个平面图形可以是矩形、
三角形或其他图形.
2.平面图形绕定直线旋转形成旋转体,这条定直线可以是平面图形的
边所在的直线,也可以不是,但定直线一定与平面图形在同一个平面 内 .
3.与多面体一样,旋转体是封闭的几何体,包括表面及其内部所有的
点 .
二、棱柱、棱锥、棱台
1.棱柱
( 1 ) 定 义 :如图8-1-1,有两个面互相平行,其余各面都 是四边形,并且相邻两个四边形的公共边都互相平行,由这 些面所围成的多面体叫做棱柱.在棱柱中,两个互相平行的面 叫做棱柱的底面,它们是全等的多边形;其余各面叫做棱柱 的侧面,它们都是平行四边形;相邻侧面的公共边叫做棱柱 的侧棱;侧面与底面的公共顶点叫做棱柱的顶点.
图8-1-1
C
>底面
顶点
侧面
侧被 — —
Fk
E-
(2)记法:棱柱用表示底面各顶点的字母来表示,如图
8.1-1中的棱柱记作棱柱ABCDEF-A'B'C'D'E'F'.
(3)分类:按底面多边形分类.
棱柱的底面可以是三角形、四边形、五边形.…,我们把
这样的棱柱分别叫做三棱柱、四棱柱、五棱柱 ….
按侧棱与底面是否垂直分类.
一般地,我们把侧棱垂直于底面的棱柱叫做直棱柱,侧棱
不垂直于底面的棱柱叫做斜棱柱.底面是正多边形的直棱柱 叫做正棱柱.底面是平行四边形的四棱柱也叫做平行六面体
归纳拓展
常见的几种四棱柱之间的转化关系
侧棱垂直
于底面
平行六面体
底面为
平行四边形
四棱柱
正方体 正四棱柱 长方体
直平行六面体
底面是 矩形
侧棱长等于 底面边长
底面是 正方形
2.棱锥
( 1 ) 定 义 :如图8-1-2,一般地,有一个面是多边
形,其余各面都是有一个公共顶点的三角形,由这些
面所围成的多面体叫做棱锥.这个多边形面叫做棱锥
的底面;有公共顶点的各个三角形面叫做棱锥的侧面;
相邻侧面的公共边叫做棱锥的侧棱;各侧面的公共顶
点叫做棱锥的顶点.
图8-1-2
(2)表示:棱锥用表示顶点和底面各顶点的字母来表示,
如图8-1-2中的棱锥记作棱锥S-ABCD.
(3)分类:棱锥的底面可以是三角形、四边形、五边
形...,我们把这样的棱锥分别叫做三棱锥、四棱锥、五棱
锥 … . . . ,其中三棱锥又叫四面体 . 底面是正多边形,并且顶
点与底面中心的连线垂直于底面的棱锥叫做正棱锥.
归纳拓展
正棱锥的相关概念及性质:
(1)正棱锥的斜高
正棱锥侧面的等腰三角形底边上的高叫做正棱锥的斜高.正棱
锥的斜高都相等.
(2)正棱锥的简单性质
各侧棱相等,各侧面都是全等的等腰三角形,斜高都相等.
正棱锥的高、斜高和斜高在底面上的射影组成一个直角三角 形;正棱锥的高、侧棱和侧棱在底面上的射影也组成一个直 角三角形.
3.棱台
(1)定义:如图8-1-3,用一个平行于棱锥底面的平面去 截棱锥,我们把底面和截面之间那部分多面体叫做棱台.在棱 台中,原棱锥的底面和截面分别叫做棱台的下底面和上底面. 类似于棱柱、棱锥,棱台也有侧面、侧棱、顶点.
图8-1-3
( 2 ) 记 法 :棱台用表示底面各顶点的字母来表示,如图
8.1-3中的棱台记作棱台ABCD-A'B'C'D'.
( 3 ) 分 类 :由三棱锥、四棱锥、五棱锥...截得的棱台分
别叫做三棱台、四棱台、五棱台...
归纳提升
棱台是用平行于棱锥底面的平面去截棱锥,底面
与截面之间的部分,这是从棱锥出发去定义棱台. 它说明了棱台与棱锥的联系,为我们提供了解决 棱台问题的一种方法,棱台问题常常转化为棱锥 问题来解决,即还台为锥.
小结&拓展
棱柱、棱锥、棱台都是多面体,它们相互之间没有公共部分;四面
体是一种特殊的棱锥(三棱锥);直棱柱和平行六面体都是棱柱, 它们又有公共部分——直平行六面体,而长方体是特殊的直平行六 面体.
1.所有棱长都相等的三棱锥叫做正四面体.
2.正三棱锥与正四面体的区别和联系
正四面体各个面都是全等的等边三角形.正四面体是正三棱锥,但正
三棱锥只有在侧棱与底面三角形边长相等时才是正四面体.
圆柱
图形及表示
定义:以矩形的一边所在直线为旋转轴,其余三边旋转形成的面 所围成的旋转体叫做圆柱
相关概念: 圆柱的轴:旋转轴.圆柱的底面:垂直于轴的边旋转而成的圆面 圆柱的侧面:平行于轴的边旋转而成的曲面. 圆柱侧面的母线:无论旋转到什么位置,不垂直于轴的边.
图中圆柱表示
为:圆柱00
轴
底面
侧面 母线
A
底面
A'
0
0
三、圆柱、圆锥、圆台和球
.
圆锥
图形及表示
定义:以直角三角形的一条直角边所在直线为为旋转轴 其余两边旋转形成的面所围成的旋转体
侧
母线
底
图中圆锥表示为圆锥SO
相关概念: 圆锥的轴:旋转轴 圆锥的底面:垂直于轴的边旋转而成的圆面 侧面:直角三角形的斜边旋转而成的曲面 母线:无论旋转到什么位置,不垂直于轴的边
圆台 图形及表示
定义:用平行于圆锥底面的平面去截圆锥,底面与截面之间的部分叫 做圆台 旋转法定义:以直角梯形中垂直于底边的腰所在直线为旋转轴,将直 角梯形绕旋转轴旋转一周而形成的旋转体叫做圆台 底面 侧 面 、 母线 底面
轴
相关概念: 圆台的轴:旋转轴 圆台的底面:垂直于轴的边旋转一周所形成的圆面 圆台的侧面:不垂直于轴的边旋转一周所形成的曲面 母线:无论旋转到什么位置,不垂直于轴的边
图中圆台表示为:圆台 O'0
球
图形及表示
定义:半圆以它的直径所在直线为旋转轴,旋转一周形 成的曲面叫做球面(是“空 心 ”的),球面所围成的旋 转体叫做球体,简称球(是“实 心 ”的) .
半径
0
直径
相关概念: 球心:半圆的圆心 半径:连接球心和球面上任意一点的线段叫做球的半径 直径:连接球面上两点并且经过球心的线段叫做球的直 径(即半圆的直径).
图中的球表示为:球O
球心
相同点 不同点
联系
棱柱 、棱 锥 、 棱台 都由平面多边 形围成,都有 底面,且底面 都是多边形 棱柱两个底面,平行且全 等;棱锥一个底面;棱台 两个底面,平行且相似
棱台是由 棱锥截取 得到的
圆柱 、圆 锥 、 圆台 都由平面多边 形旋转形成, 都有底面,且 底面都是圆面 圆柱两个底面,是半径相 等的圆面;圆锥一个底面 ,是圆面;圆台两个底面 ,是不全等但相似的圆面
圆台是由 圆锥截取 得到的
空间几何体在结构上的相同点和不同点及联系
柱体 上底扩大 台体 上底缩小 锥体
四 . 简单组合体
(1)定义:由简单几何体组合而成的几何体
称作简单组合体.
(2)构成形式:
①由简单几何体拼接而成.
②由简单几何体截去或挖去一部分而成.
常考题型
一 . 空间几何体概念的理解
<1>柱、锥、台、球的结构特征
例1.下列说法正确的是 ( )
A.各个面都是三角形的几何体是三棱锥
B.多面体至少有三个面
C.各侧面都是正方形的四棱柱一定是正方体
D.九棱柱有9条侧棱,9个侧面,侧面为平行四边形
【解析】 选 项A 错,反例如图8-1-4;一个多面体至少有四
个面,如三棱锥有四个面,不存在只有三个面的多面体,所 以选项B错;选项C错,上、下底面是全等的菱形,各侧面是 全等的正方形,它不是正方体;根据棱柱的定义,知选项D 正确.
图8-1-4
【答案】 D
训练题1
1下列三个命题中,正确的有( )
①棱柱中互相平行的两个面叫做棱柱的底面;②有两
个面互相平行,其余四个面都是等腰梯形的六面体是 棱台;③四棱锥有4个顶点.
A.0个 B.1 个 C.2 个 D.3 个
1.A 解析:①错误,底面为正六边形的棱柱相对的两
个侧面互相平行,但不能作为底面.②错误,因为不能 保证侧棱相交于同一点.③错误,四棱锥只有一个顶点, 就是各侧面的公共顶点.
训练题2
下列叙述中正确的个数是 ( )
①以直角三角形的一边所在直线为轴旋转所得的旋转体
是圆锥;
②以直角梯形的一腰所在直线为轴旋转所得的旋转体是
圆台;
③半圆绕其直径所在的直线旋转一周所形成的曲面是球;
④用一个平面去截圆锥,得到一个圆锥和一个圆台.
A.0 B.1 C.2 D.3
2.A 解析:①错误,应以直角三角形的一条直角边所在直线
为轴;(2)错误,应以直角梯形的垂直于底边的腰所在直线为轴;
③错误,应把“球”改成“球面”;④错误,应是用一个与底 面平行的平面去截圆锥.
训练题3
下列说法:(1)圆柱的底面是圆面;(2)经过圆柱任意两条母线的截面
是一个矩形面;(3)圆台的任意两条母线的延长线,可能相交,也可能不 相交;(4)夹在圆柱的两个截面间的几何体还是一个旋转体.其中正确的 是
3 . (1)(2)解析:(1)正确,圆柱的底面是圆面;(2)正确,经过
圆柱任意两条母线的截面是一个矩形面;(3)不正确,圆台的母线延长 后相交于一点;(4)不正确,夹在圆柱的两个平行于底面的截面间的几 何体才是旋转体.
特别提示:(1)对多面体的判断, 一定要紧扣棱柱、棱锥、棱
台的结构特征,注意概念中的特殊字眼,切不可马虎大意,如 棱柱的概念中的“相邻”,棱锥的概念中的“公共顶点”,棱 台的概念中的“棱锥”等.
(2)圆柱、圆锥、圆台和球都是由一个平面图形绕其特定边(直
径)所在的直线旋转而成的几何体,必须准确认识各旋转体对 旋转轴的具体要求.只有理解了各旋转体的形成过程,才能明确 由此产生的母线、轴、底面等概念,进而判断与这些概念有关 的命题的真假.
(1) (2) (3)
图8-1-5
【解题提示】结合简单组合体的两种基本构成形式入手分析.
【解】 图8-1-5(1)所示的几何体是由两个圆台拼接而成
的组合体;图8-1-5(2)所示的几何体是由一个圆台挖去一 个圆锥得到的组合体;图8-1-5(3)所示的几何体是在一个 圆柱中间挖去一个三棱柱后得到的组合体.
<2>简单组合体的结构特征
例2.描述下列几何体的结构特征.
训练题4[2019·湖南长沙雨花区检测]如图8-1-6(1)(2)
所示,绕虚线旋转一周后形成的旋转体是由哪些简单几何体
(1) (2)
图8-1-6
组成的
4.解:如图D-8-1所示,其中图(1)是由一个圆柱O O
和圆台O O 、 圆 台O O 组成的;图(2)是由一个圆锥 O O 、 一个圆柱O O 及一个圆台O O 中挖去圆锥O O 组成的.
(1) (2)
图D-8-1
判断实物是由哪些简单几何体组成的技巧
(1)准确理解简单几何体(柱、锥、台、球)的结构特征.
(2)正确掌握简单组合体构成的两种基本形式.
(3)若用分割的方法,则需要根据几何体的结构特征恰当地作
出辅助线(或面) .
二 . 空间几何体的侧面展开图
例3.如图8-1-7所示,在以O为顶点的三棱锥中,过O的三
条棱两两的交角都是30°,在一条棱上有A,B 两 点 ,OA=4,
OB=3 ,以A ,B为端点用一条绳子紧绕三棱锥的侧面一周(绳
和侧面无摩擦),求此绳在A,B 之间的最短绳长.
图8-1-7
图8-1-8
A,B 两点间的最短绳长就是线段AB的长度.因为OA=4,
OB=3,∠AOB=90°, 所以AB=5, 即此绳在A,B 之间的
最短绳长为5.
【解】 作出三棱锥的侧面展开图,如图8-1-8.
【解题提示】
把点A,B 所在侧棱剪开, 再将三棱锥侧面展开
利用平面几何 知识求解问题
训练题5[2019·安徽合肥高一检测]如图8-1-9,圆锥的底
面半径为r, 母线长为4r, 一细绳从A点开始,绕圆锥侧面一 圈又回到A点,试求细绳的最短长度.
图8-1-9
图D-8-2
∵圆锥的底面半径为r,
∴I=2πr.∵ 以母线长4r为半径的圆的周长为I=8πr,
. , ∴∠ASA'=90° .
∴AA'=4 √2 r..:.细绳的最短长度为4 √2r.
5.解:把圆锥的侧面沿SA剪开并展开在平面内得一扇形,
如图D-8-2, 则细绳的最短长度即线段AA'的长度.
求空间几何体表面上两点间的最短距离问题的常用方法
求空间几何体表面上两点间的最短距离问题,常常要归结为
求平面上两点间的最短距离问题,因此解决这类问题的方法 就是先把空间几何体的侧面展开成平面图形,再用平面几何 的知识来求解.
训练题6.[2019·陕西西安未央区期末]某人用如图8-1-10
所示的纸片,沿折痕折后粘成一个四棱锥形的“走马灯”
正方形做灯底,且有一个三角形面上写上了“年”字,当灯
旋转时,正好看到“新年快乐”的字样,则在①②③处应依 次 写 上 ( )
图8-1-10
A.快、新、乐 B.乐、新、快 C.新、乐、快 D.乐、快、新
6.A 解析:根据四棱锥图形,正好看到“新年快乐”
的字样时选项A 正确.
【名师点拨】
解答展开与折叠问题,要结合空间几何体的定义和结
构特征,发挥空间想象能力.必要时可制作侧面展开图 进行实践操作.
① ② ③
图8-1-11
则原几何体应为:
① ,②_ ,③_
____
训练题7.如图8-1-11是三个几何体的平面展开图,
7.五棱柱五棱锥三棱台解析:各展开图对应的几何
故①是五棱柱,②是五棱锥,③是三棱台.
①
图D-8-3
体如图D-8-3 所示.
②
③
三 . 空间几何体的轴截面及计算问题
例4.一个圆锥的底面半径为2 cm, 高为6 cm,
在圆锥内部有一个高为x cm的内接圆柱.
( 1 ) 用x表示圆柱的轴截面面积S.
( 2 ) 当x为何值时,S 最大
(1)设圆柱的底面半径为r cm,
f
∴当x=3时,S取得最大值,Smax=6 cm .
【解】
则由
训练题8.
[2019·江苏泰州姜堰区检测]圆台上底面面积为π,下底面面积为
16π,用一个平行于底面的平面去截圆台,该平面自上而下分圆台的 高的比为2:1,求这个截面的面积.
图D-8-4
过点D作DF⊥AB于点F, 交GH于点E.由题意知DO =1,
AO =4,∴AF=3.
∵DE=2EF,∴DF=3EF,∴ , ∴GE=2.
∴圆O 的半径为3,∴这个截面的面积为9π.
8.解:圆台的轴截面如图D-8-4所示,O ,O ,O
为上底面、下底面、截面的圆心.
分别
【名师点拨】
1.圆锥的轴截面是以2r(r为圆锥的底面半径)为底边,I(I为
圆锥的母线长)为腰的等腰三角形.
2.圆柱的轴截面是以2r(r为圆柱的底面半径)和I(I 为圆柱的
母线长)为相邻两边的矩形.
3.圆台的轴截面是以2r ,2r 为 底 ,I(I 为圆台的母线长)为
腰的等腰梯形.
四易错易混问题
<1>对棱柱、棱锥、棱台的概念理解不到位致误
例5.如图8-1-12,甲、乙、丙分别是棱柱、棱锥、棱台吗
图8-1-12
为什么
丙
甲
乙
【解】 图甲不是棱柱,因为虽然上、下两个面平行,但是
四边形ABB A 与四边形A B B A 不在一个平面内,所以多
边形ABB B A A 不是一个平面图形,它更不是一个平行四
边形,所以这个几何体不是棱柱;图乙不是棱锥,因为它的
六个三角形没有一个公共点,故不是棱锥,只是一个多面体;
图丙不是棱台,因为其侧棱的延长线不能相交于同一点.
【防错有术】
切实理解棱柱、棱锥和棱台的定义是解答此类问题 的关键 .
<2>画错截面图致错
例6.在底面半径为3,高为6的圆锥内有一个内接正方体,
求内接正方体的棱长.
则OO'=6,O'M=3,AA'=a,AC'=√2a,:
解得a=6 √2-6.
∴内接正方体的棱长为6 √2-6.
【解】 设正方体的棱长为a, 此空间几何体的示意图如图
8-1-13,作轴截面如图8-1-14,
图8-1-14
图8-1-13
,
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
