人教A版(2019)高中数学必修第一册4.2.2指数函数的图象与性质 课件(共14张PPT)
文档属性
| 名称 | 人教A版(2019)高中数学必修第一册4.2.2指数函数的图象与性质 课件(共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-06 20:10:30 | ||
图片预览






文档简介
(共14张PPT)
4.2.2 指数函数的图象 和性质
式子 名称
a X
y
指数函数:y=a 底数 指数
幂值
幂函数:y=x" 指数 底数
幂值
温故知新
幂西数与指数函数的对比
判断一个函数是幂函数还是指数函数切入点
看看未知数x是指数还是底数
幂函数
指报函数
2、研究幂函数性质时,有哪些步骤,研究哪些方面性质
(1)描点,作出图象,由图象得到函数性质
(2)研究内容:函数三要素,单调性,奇偶性,特殊点
类比研究幂函数性质的过程和方法,我们来研究指数函数。
先画简单的函数=2'的图象先完成下表,再画图象
X
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
0.25
0.35
0.5
0.71
1
1.41
2
2.83
4
-3-2-10 123
y
1
完成下表:
对比y=(
与y=2取
值的列表,有
什么关系
X y 函数y=2图象上 任意一点P(x,y)
-2 0.25
-1.5 0.35
-1 0.5 关于y轴的对称点 P(-x,y)都在函数
-0.5 0.71
-)
的图象上
0 1
0.5 1.41
1 2
1.5 2.83
2 4
X
y
-2
4
-1.5
2.83
-1
2
-0.5
1.41
0
1
0.5
0.71
1
0.5
1.5
0.35
2
0.25
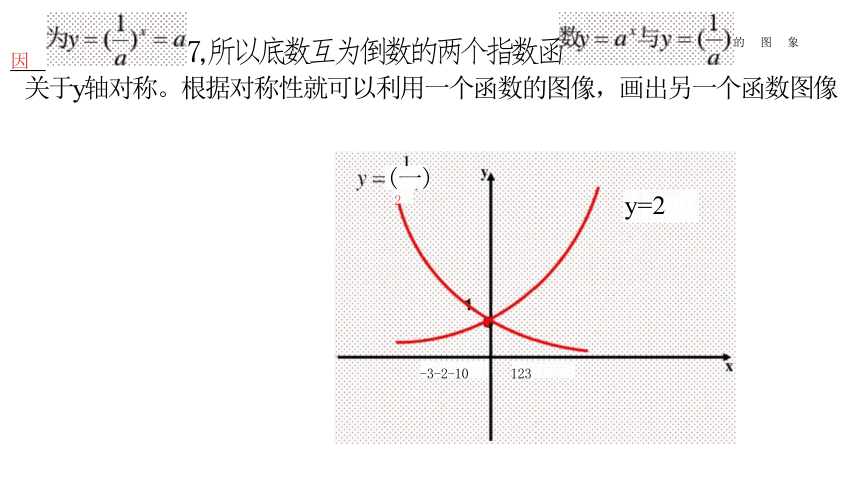
再画y=( 图象 .
y=(2
因 7,所以底数互为倒数的两个指数函 的图象
关于y轴对称。根据对称性就可以利用一个函数的图像,画出另一个函数图像
(一)
2 y=2
-3-2-10 123
4 y y=4*y=3
y=2×
1
12 3 x
-3-2-10 1 2 3 x 3-2 -10 123 x
R
(0,+00)
(1)过定点(0,1)
(2)减函数 (3)增函数
y
y=a
指数函数的图像和性质
【二】指数函数的性质:在 同一坐标系中作出底数不同的指数函数图像
一般地指数函数的图像和性质如下表所示
y=a
图像
定义域
值域
性质
y-()
3 -21
0a>1
0
1
[1]指数函数既不是奇函数也不是偶函数
【2】指数函数在y轴右侧的图像,底数越大
图像越高( 底大图高)
【3]①当a > 1且x>0 时,y > 1
②当 a>1 且x<0 时,0③当 0< a < 1 且x>0 时,0 < y < 1 ④当 0< a<1 且x <0 时,y > 1
【4】指数函数图像下端与 x 轴无限接近
但永不相交
y=() ) y y=4* y=3
()
1
3-2-10
12 3 x
y=2×
a>1 0图 象 1 0 X
性 质 (1)定义域 R
(2)值域 (0,+oo)
(3)过定点 (0,1)
(4)单调性增函数 (4)单调性:减函数
(5)奇偶性 非奇非偶 (5)奇偶性
非奇非偶
(6)当x>0时 ,y>1. 当x<0时 ,0o时 ,01.
指数函数的图象和性质
指数函数的应用
【例题】比较下列各题中两个值的大小
(1)1.725和1.7 (2)0.8 √ 和0.8- (3)1.703和0.931
【解】(1)函数 y=1.7 是增函数,且2.5<3,则1.725<173
(2)函数y=0.8* 是减函数,且- √ 3<- √ 2,则08-2<0.8-V3
(3) ∵1.7 >1.7°=1;
又∵0.9 <0.9°=1;
∴0.9 <1.7°3
变式:若a=0.6 ,b=0.6',c=1.5°6, 则a,b,c 的大小关系
解:∵y=0.6 是减函数又∵0.6<1.5:.0.6 >0.6
∵y=x°6 是增函数,又:0.6<1.5..0.6 <1.56
∴0.6 <0.6° <1.5°6即b例4 如 图,某城市人口呈指数增长
(1)根据图象,估计城市人回每翻一番
所需的时间(倍增期)
(2)该城市人口从80万人开始,经过20
年会增长到多少万人
分析该城市人回指数增长,同一个函数的倍增期是相同。
解:( 1)从图象,可发现该城市人国经过20
年约为10万人,经过40年约为20万人,即10
万人增长到20万人所用的时间为20年,所以
该城市人回每一翻一番所需的时间为20年。
(2)因为倍增期为20年。所以每经过20年,人口将翻一番。因此,从 80年人开始,经过20年,该城市人口大约会增长到160万人。
a>1 0图 象 y 0 X
性 质 (1)定义域 R
(2)值域 (0,+o0)
(3)过定点 (0,1)
(4)单调性,增函数
(4)单调性减函数
(5)奇偶性 非奇非偶
(5)奇偶性非奇非偶
(6)当x>0时 ,y>1 当x<0时 ,0(6)当x>0时 ,0当x<0时 ,y>1.
课堂小结 指数函数图象与性质
小试牛刀
1
1.函数f(x)=2* 在区间-1,3]上最小值是 2
2 . 函数(x)=() 在区间 - 13 上最小值是
3.函数f(x)= √3*-27 的定义域是(3,+)
4函数(0--277的定义域是(-o,-3)
4.2.2 指数函数的图象 和性质
式子 名称
a X
y
指数函数:y=a 底数 指数
幂值
幂函数:y=x" 指数 底数
幂值
温故知新
幂西数与指数函数的对比
判断一个函数是幂函数还是指数函数切入点
看看未知数x是指数还是底数
幂函数
指报函数
2、研究幂函数性质时,有哪些步骤,研究哪些方面性质
(1)描点,作出图象,由图象得到函数性质
(2)研究内容:函数三要素,单调性,奇偶性,特殊点
类比研究幂函数性质的过程和方法,我们来研究指数函数。
先画简单的函数=2'的图象先完成下表,再画图象
X
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
0.25
0.35
0.5
0.71
1
1.41
2
2.83
4
-3-2-10 123
y
1
完成下表:
对比y=(
与y=2取
值的列表,有
什么关系
X y 函数y=2图象上 任意一点P(x,y)
-2 0.25
-1.5 0.35
-1 0.5 关于y轴的对称点 P(-x,y)都在函数
-0.5 0.71
-)
的图象上
0 1
0.5 1.41
1 2
1.5 2.83
2 4
X
y
-2
4
-1.5
2.83
-1
2
-0.5
1.41
0
1
0.5
0.71
1
0.5
1.5
0.35
2
0.25
再画y=( 图象 .
y=(2
因 7,所以底数互为倒数的两个指数函 的图象
关于y轴对称。根据对称性就可以利用一个函数的图像,画出另一个函数图像
(一)
2 y=2
-3-2-10 123
4 y y=4*y=3
y=2×
1
12 3 x
-3-2-10 1 2 3 x 3-2 -10 123 x
R
(0,+00)
(1)过定点(0,1)
(2)减函数 (3)增函数
y
y=a
指数函数的图像和性质
【二】指数函数的性质:在 同一坐标系中作出底数不同的指数函数图像
一般地指数函数的图像和性质如下表所示
y=a
图像
定义域
值域
性质
y-()
3 -21
0
0
1
[1]指数函数既不是奇函数也不是偶函数
【2】指数函数在y轴右侧的图像,底数越大
图像越高( 底大图高)
【3]①当a > 1且x>0 时,y > 1
②当 a>1 且x<0 时,0
【4】指数函数图像下端与 x 轴无限接近
但永不相交
y=() ) y y=4* y=3
()
1
3-2-10
12 3 x
y=2×
a>1 0
性 质 (1)定义域 R
(2)值域 (0,+oo)
(3)过定点 (0,1)
(4)单调性增函数 (4)单调性:减函数
(5)奇偶性 非奇非偶 (5)奇偶性
非奇非偶
(6)当x>0时 ,y>1. 当x<0时 ,0
指数函数的图象和性质
指数函数的应用
【例题】比较下列各题中两个值的大小
(1)1.725和1.7 (2)0.8 √ 和0.8- (3)1.703和0.931
【解】(1)函数 y=1.7 是增函数,且2.5<3,则1.725<173
(2)函数y=0.8* 是减函数,且- √ 3<- √ 2,则08-2<0.8-V3
(3) ∵1.7 >1.7°=1;
又∵0.9 <0.9°=1;
∴0.9 <1.7°3
变式:若a=0.6 ,b=0.6',c=1.5°6, 则a,b,c 的大小关系
解:∵y=0.6 是减函数又∵0.6<1.5:.0.6 >0.6
∵y=x°6 是增函数,又:0.6<1.5..0.6 <1.56
∴0.6 <0.6° <1.5°6即b
(1)根据图象,估计城市人回每翻一番
所需的时间(倍增期)
(2)该城市人口从80万人开始,经过20
年会增长到多少万人
分析该城市人回指数增长,同一个函数的倍增期是相同。
解:( 1)从图象,可发现该城市人国经过20
年约为10万人,经过40年约为20万人,即10
万人增长到20万人所用的时间为20年,所以
该城市人回每一翻一番所需的时间为20年。
(2)因为倍增期为20年。所以每经过20年,人口将翻一番。因此,从 80年人开始,经过20年,该城市人口大约会增长到160万人。
a>1 0
性 质 (1)定义域 R
(2)值域 (0,+o0)
(3)过定点 (0,1)
(4)单调性,增函数
(4)单调性减函数
(5)奇偶性 非奇非偶
(5)奇偶性非奇非偶
(6)当x>0时 ,y>1 当x<0时 ,0
课堂小结 指数函数图象与性质
小试牛刀
1
1.函数f(x)=2* 在区间-1,3]上最小值是 2
2 . 函数(x)=() 在区间 - 13 上最小值是
3.函数f(x)= √3*-27 的定义域是(3,+)
4函数(0--277的定义域是(-o,-3)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
