人教A版高中数学必修第一册 同角三角函数的基本关系 课件(2)(共35张PPT)
文档属性
| 名称 | 人教A版高中数学必修第一册 同角三角函数的基本关系 课件(2)(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-06 20:14:32 | ||
图片预览








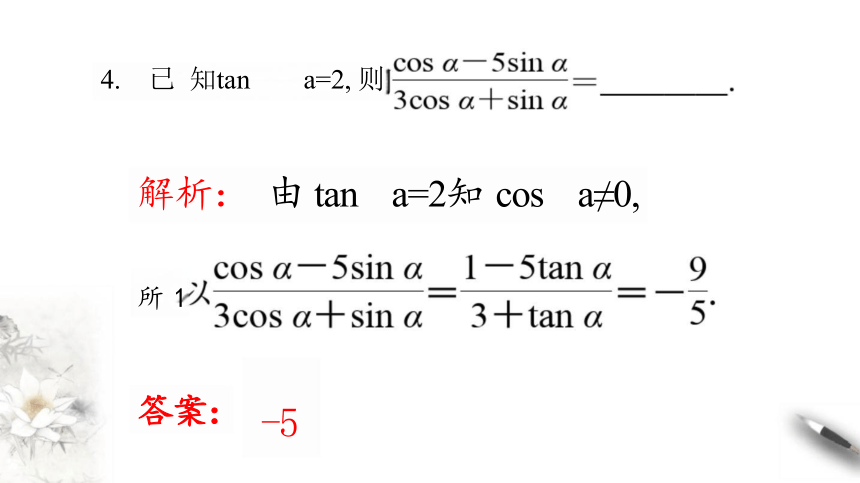

文档简介
(共34张PPT)
人教2019版必修第一册
第五章三角函数
5.2.2同角三角函数的基本关系
课程目标
1.理解并掌握同角三角函数基本关系式的推导及 应用.
2.会利用同角三角函数的基本关系式进行化简、 求值与恒等式证明.
数学学科素养
1.数学抽象:理解同角三角函数基本关系式;
2.逻辑推理: “sin α±cos α” 同 “sin acos α” 间的关 系;
3.数学运算:利用同角三角函数的基本关系式进行化 简、求值与恒等式证明.
自主预习,回答问题
阅读课本182-183页,思考并完成以下问题
1. 同角三角函数的基本关系式有哪两种
2. 同角三角函数的基本关系式适合任意角吗
·要求: 学生独立完成,以小组为单位,组内可商量,最终选出代表回答问题。
知识清单
同角三角函数的基本关系
(1)平方关系: sin a+cos α= 1 .
商数关系:
(2)语言叙述:同一个角a 的正弦、余弦的平方和_ 等 于 1 ,商 等
于角α的正切.
思考: “ 同角”一词的含义是什么
[提示] 一是“角相同”,如sin a+cos β=1就不一定成立.二
是对任意一个角(在使得函数有意义的前提下),关系式都成立,即与 角的表达式形式无关,如sin 15°+cos 15°=1,
小试牛刀
1.判断(正确的打“ √ ”,错误的打“”.)
(1)对任意角a,sin 3a+cos 3a=1 都成立 . ( )
(2)对任意角 都成立. ( )
(3)若 则 .( )
解 析: (1) √ .符合同角三角函数的关系.
(2)×.等式 的条件
即α≠π+2kπ,k∈Z.
(3)×.因为α的范围不明确,故
答案: (1) √ (2)×(3)×
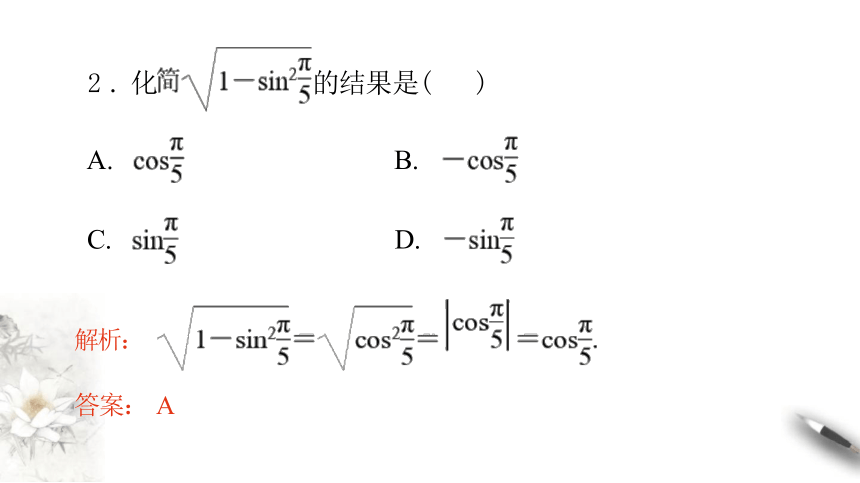
2 . 化 的结果是( )
A. B.
C. D.
解析:
答案: A
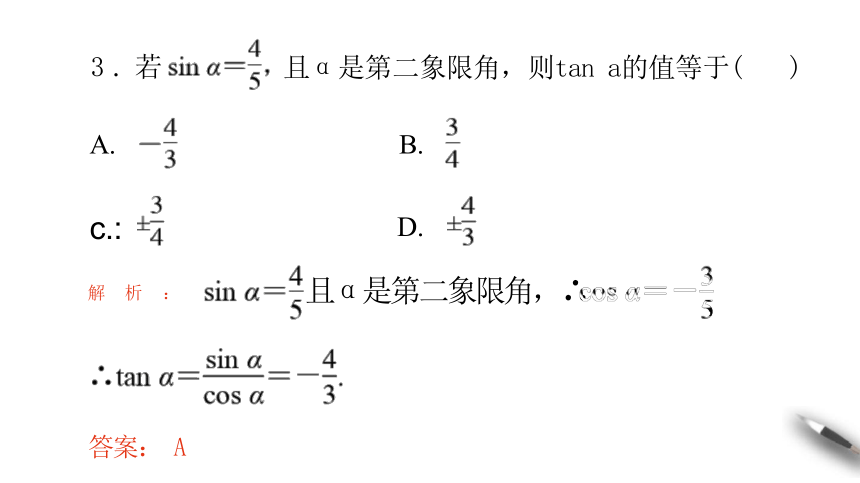
3 . 若 且α是第二象限角,则tan a的值等于( )
A. B.
c.: D.
解 析 : 且α是第二象限角,∴
答案: A
解析: 由 tan a=2知 cos a≠0,
所 1
答案: -5
4. 已 知tan a=2, 则
题型分析 举一反三
题型一应用同角三角函数关系求值
【例1】 (1)若 求 cos a,tan a的值;
(2)已知 求 sin a,tan a的值 .
解析:(1): ,a 是第三、第四象限角,
当α是第三象限角时,
a 是第四象限角时,
:
(2) ∵
∴α是第二或第三象限的角. 如果a 是第二象限角,那么
如果α是第三象限角,同理可得
事
(1)已知角α的某一种三角函数值,求角α的其余三角函数值,
要注意公式的合理选择, 一般是先选用平方关系,再用商数关系.
(2)若角α所在的象限已经确定,求另两种三角函数值时,只有
一组结果;若角α所在的象限不确定,应分类讨论, 一般有两组结
果 .
提醒:应用平方关系求三角函数值时,要注意有关角终边位置的
判断,确定所求值的符号.
解 题 方 法(利用同角三角函数的基本关系解决给值求值问题的方法)
[跟踪训练一]
1. 已知sin a+3cos a=0,求 sin a,cos a的值.
解析: ∵sin a+3cos a=0,
∴.sin a=—3cos a.
又 sin a+cos a=1,
∴(-3cos a) +cos a=1,
∴角a 的终边在第二或第四象限.
当角α的终边在第二象限时,
当角a 的终边在第四象限时,
又由sin a=—3cos a,可知 sin a 与 cos a 异号,
即10cos a=1,
事
心
●
题型二三角函数式的化简、求值
【例2】 (1)化简:
(2)若角α是第二象限角,化简:
思路点拨:( 1)利用平方关系代换“1”
构造完全平方 于 化简求值
(2)切化弦 化简求值
第二象限角,所以sin a>0,cos a<0,
解析: (1)原式=
因为α是
解 题 方 法(化简三角函数式的常用方法)
(1)切化弦,即把非正弦、余弦函数都化成正弦、余弦函数,从而
减少函数种类以便化简.
(2)对含有根号的,常把根号下式子化成完全平方式,然后去根号
达到化简的目的
(3)对于化简高次的三角函数式,往往借助于因式分解,或用“1”
的代换,以降低函数次数,达到化简目的.
提醒:在应用平方关系式求 sin a 或 cos a 时,其正负号是由角a
所在的象限决定,不可凭空想象.
[跟踪训练二]
1. 化简:
题型三三角函数式的证明
【例3】 求证:
证明:由cosx≠0, 知sinx≠-1, 所以1+sinx≠0, 于是
所以,原式成立.
解 题 方 法(三角函数式解题思路及解题技巧)
1. 证明恒等式常用的思路是:(1)从一边证到另一边, 一般由繁
到简;(2)左右开弓,即证左边、右边都等于第三者;(3)比较法(作差, 作比法).
2.常用的技巧有:(1)巧用“1”的代换;(2)化切为弦;(3)多项式
运算技巧的应用(分解因式).
3. 解决此类问题要有整体代换思想.
[跟踪训练三]
1. 求证:
∴原等式成立.
证 明 :
题型四“sin a±cos α”同“sin acos α”间的关系
【例4】 已知 且0求:(1)sin acos a的值;
(2)求sin a—cos a的值.
又∵0.sin a>0,cos a<0,∴sin a—cos a>0,
解析:(1): ,∴
, 即
∴1+
重
解题方法( “sin a±cos a”同“sin acos a”间的关系)
(1)已知sin θ±cosθ求 sin θcos θ,只需平方便可.
(2)已知 sin θcosθ求 sin θ±cosθ时需开方,此时要根据已知角θ的范
围,确定sinθ±cosθ 的正负.
[跟踪训练四]
1.已知 ,a∈(0,π), 则tan a= .
解 析:法 一:(构建方程组)
因为 ,①
因为α∈(0,π),所以sin a>0,cos a<0.
由①②解得
所以
4
整理得60tan a+169tan a+60=0,解得
tan
法二:(弦化切)
同法一求出
知|sin a|>|cos a,故
a=
[跟踪训练四]
2.已知
,计算下列各式的值:
(2)sin a-2sin acos a+1.
解析: 由
化简得sin a=3cos a,
所以tan a=3.
(2)
人教2019版必修第一册
第五章三角函数
5.2.2同角三角函数的基本关系
课程目标
1.理解并掌握同角三角函数基本关系式的推导及 应用.
2.会利用同角三角函数的基本关系式进行化简、 求值与恒等式证明.
数学学科素养
1.数学抽象:理解同角三角函数基本关系式;
2.逻辑推理: “sin α±cos α” 同 “sin acos α” 间的关 系;
3.数学运算:利用同角三角函数的基本关系式进行化 简、求值与恒等式证明.
自主预习,回答问题
阅读课本182-183页,思考并完成以下问题
1. 同角三角函数的基本关系式有哪两种
2. 同角三角函数的基本关系式适合任意角吗
·要求: 学生独立完成,以小组为单位,组内可商量,最终选出代表回答问题。
知识清单
同角三角函数的基本关系
(1)平方关系: sin a+cos α= 1 .
商数关系:
(2)语言叙述:同一个角a 的正弦、余弦的平方和_ 等 于 1 ,商 等
于角α的正切.
思考: “ 同角”一词的含义是什么
[提示] 一是“角相同”,如sin a+cos β=1就不一定成立.二
是对任意一个角(在使得函数有意义的前提下),关系式都成立,即与 角的表达式形式无关,如sin 15°+cos 15°=1,
小试牛刀
1.判断(正确的打“ √ ”,错误的打“”.)
(1)对任意角a,sin 3a+cos 3a=1 都成立 . ( )
(2)对任意角 都成立. ( )
(3)若 则 .( )
解 析: (1) √ .符合同角三角函数的关系.
(2)×.等式 的条件
即α≠π+2kπ,k∈Z.
(3)×.因为α的范围不明确,故
答案: (1) √ (2)×(3)×
2 . 化 的结果是( )
A. B.
C. D.
解析:
答案: A
3 . 若 且α是第二象限角,则tan a的值等于( )
A. B.
c.: D.
解 析 : 且α是第二象限角,∴
答案: A
解析: 由 tan a=2知 cos a≠0,
所 1
答案: -5
4. 已 知tan a=2, 则
题型分析 举一反三
题型一应用同角三角函数关系求值
【例1】 (1)若 求 cos a,tan a的值;
(2)已知 求 sin a,tan a的值 .
解析:(1): ,a 是第三、第四象限角,
当α是第三象限角时,
a 是第四象限角时,
:
(2) ∵
∴α是第二或第三象限的角. 如果a 是第二象限角,那么
如果α是第三象限角,同理可得
事
(1)已知角α的某一种三角函数值,求角α的其余三角函数值,
要注意公式的合理选择, 一般是先选用平方关系,再用商数关系.
(2)若角α所在的象限已经确定,求另两种三角函数值时,只有
一组结果;若角α所在的象限不确定,应分类讨论, 一般有两组结
果 .
提醒:应用平方关系求三角函数值时,要注意有关角终边位置的
判断,确定所求值的符号.
解 题 方 法(利用同角三角函数的基本关系解决给值求值问题的方法)
[跟踪训练一]
1. 已知sin a+3cos a=0,求 sin a,cos a的值.
解析: ∵sin a+3cos a=0,
∴.sin a=—3cos a.
又 sin a+cos a=1,
∴(-3cos a) +cos a=1,
∴角a 的终边在第二或第四象限.
当角α的终边在第二象限时,
当角a 的终边在第四象限时,
又由sin a=—3cos a,可知 sin a 与 cos a 异号,
即10cos a=1,
事
心
●
题型二三角函数式的化简、求值
【例2】 (1)化简:
(2)若角α是第二象限角,化简:
思路点拨:( 1)利用平方关系代换“1”
构造完全平方 于 化简求值
(2)切化弦 化简求值
第二象限角,所以sin a>0,cos a<0,
解析: (1)原式=
因为α是
解 题 方 法(化简三角函数式的常用方法)
(1)切化弦,即把非正弦、余弦函数都化成正弦、余弦函数,从而
减少函数种类以便化简.
(2)对含有根号的,常把根号下式子化成完全平方式,然后去根号
达到化简的目的
(3)对于化简高次的三角函数式,往往借助于因式分解,或用“1”
的代换,以降低函数次数,达到化简目的.
提醒:在应用平方关系式求 sin a 或 cos a 时,其正负号是由角a
所在的象限决定,不可凭空想象.
[跟踪训练二]
1. 化简:
题型三三角函数式的证明
【例3】 求证:
证明:由cosx≠0, 知sinx≠-1, 所以1+sinx≠0, 于是
所以,原式成立.
解 题 方 法(三角函数式解题思路及解题技巧)
1. 证明恒等式常用的思路是:(1)从一边证到另一边, 一般由繁
到简;(2)左右开弓,即证左边、右边都等于第三者;(3)比较法(作差, 作比法).
2.常用的技巧有:(1)巧用“1”的代换;(2)化切为弦;(3)多项式
运算技巧的应用(分解因式).
3. 解决此类问题要有整体代换思想.
[跟踪训练三]
1. 求证:
∴原等式成立.
证 明 :
题型四“sin a±cos α”同“sin acos α”间的关系
【例4】 已知 且0
(2)求sin a—cos a的值.
又∵0
解析:(1): ,∴
, 即
∴1+
重
解题方法( “sin a±cos a”同“sin acos a”间的关系)
(1)已知sin θ±cosθ求 sin θcos θ,只需平方便可.
(2)已知 sin θcosθ求 sin θ±cosθ时需开方,此时要根据已知角θ的范
围,确定sinθ±cosθ 的正负.
[跟踪训练四]
1.已知 ,a∈(0,π), 则tan a= .
解 析:法 一:(构建方程组)
因为 ,①
因为α∈(0,π),所以sin a>0,cos a<0.
由①②解得
所以
4
整理得60tan a+169tan a+60=0,解得
tan
法二:(弦化切)
同法一求出
知|sin a|>|cos a,故
a=
[跟踪训练四]
2.已知
,计算下列各式的值:
(2)sin a-2sin acos a+1.
解析: 由
化简得sin a=3cos a,
所以tan a=3.
(2)
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
