数学人教A版(2019)选择性必修第一册2.5.2圆与圆的位置关系 课件(共29张PPT)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.5.2圆与圆的位置关系 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-06 20:22:44 | ||
图片预览






文档简介
(共29张PPT)
2.5.2圆与圆的位置关系
人教A版(2019)高中数学选择性必修一第二章2.5《直线与圆、圆与圆的位置关系》
问题: 如何判断直线与圆的位置关系
代数法:
直线与圆相交,有两个交点,可通过两
△>0 方程有两解 点坐标公式求弦长
△=0 方程有一解 直线与圆相切,有一个交点
△<0 方程有0解 直线与圆相离,无交点
复习回顾
问题: 如何判断直线与圆的位置关系
几何法:
dd=r, 直线与圆相切,有一个交点 d>r, 直线与圆相离,无交点
复习回顾
前面我们运用直线的方程、圆的方程,研究了直线与圆的 位置关系.
现在我们类比上述研究方法,运用圆的方程,通过定量计 算研究圆与圆的位置关系.
新课导入
探究新知 圆与圆的位置关系
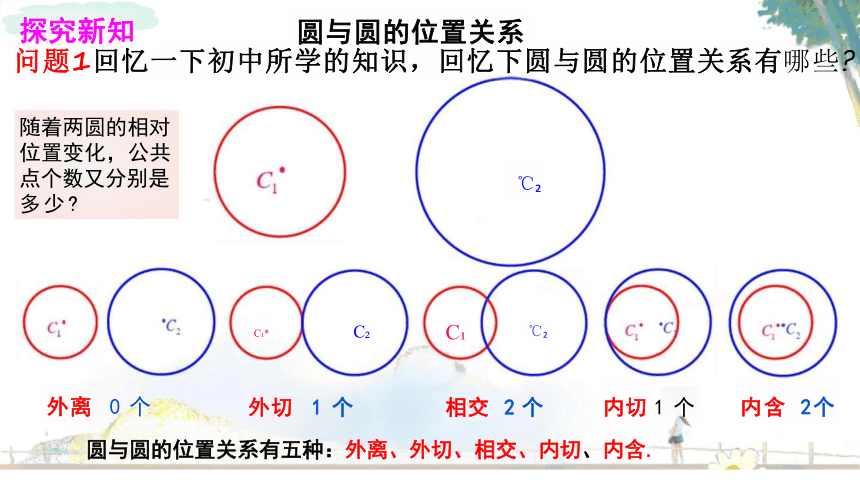
问题1回忆一下初中所学的知识,回忆下圆与圆的位置关系有哪些
外离 0 个 外切 1 个 相交 2 个 内切 1 个
圆与圆的位置关系有五种:外离、外切、相交、内切、内含.
随着两圆的相对 位置变化,公共 点个数又分别是 多少
内含 2个
℃
C
℃
C
C *
1.代数法:联立两者方程看是否有解.
(1)由两个圆的方程
(2)消去y(或x)得到关于x(或y)的一元二次方程;
(3)求出△;
(4)判断△的符号,得出结论:
① 方程组有两组不同实数解→ 两 圆相交
②方程组有 一组实数解 两 圆 相切
③ 方程组没有实数解 两圆相离或内含
探究新知 圆与圆的位置关系
问题2类比适用直线和圆的方程,研究直线与圆的位置关系的方 法,如何利用圆的方程,判断它们之间的位置关系
利用圆的方程判断圆与圆位置关系:
联立求解.
(2)求出两圆的圆
心坐标及半径r r ;
(3)求两圆的圆
心距d;
(4)比较d 与Ir -r I, r +r 的大小关系, 得出结论:
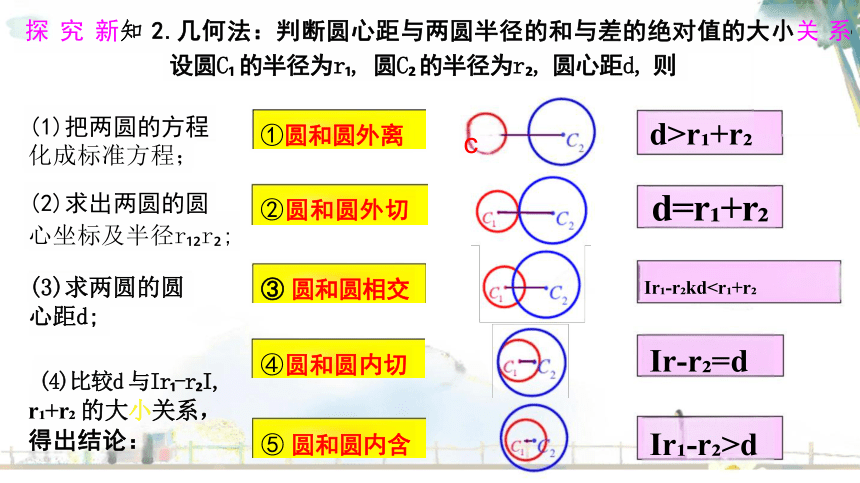
探 究 新知 2.几何法:判断圆心距与两圆半径的和与差的绝对值的大小关 系
设圆C 的半径为r , 圆C 的半径为r , 圆心距d, 则
d=r +r
Ir -r kdIr-r =d
Ir -r >d
(1)把两圆的方程 化成标准方程;
②圆和圆外切
③ 圆和圆相交
⑤ 圆和圆内含
④圆和圆内切
①圆和圆外离
d>r +r
c
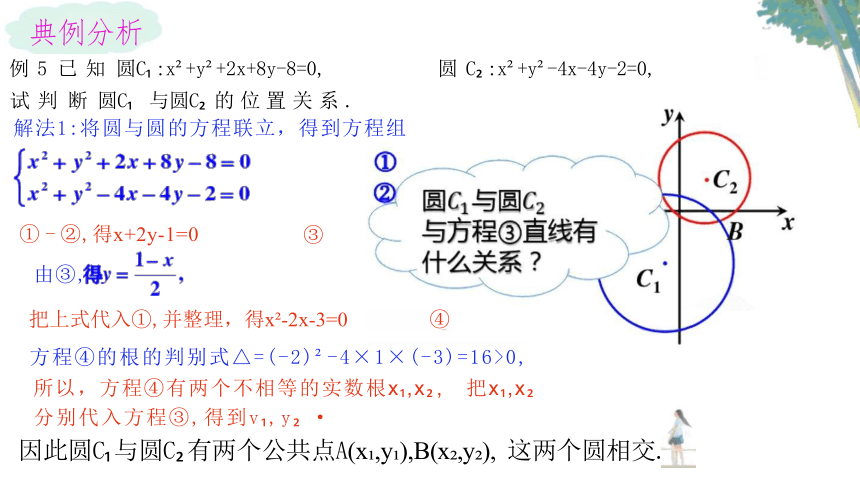
① - ②,得x+2y-1=0 ③
由③,
把上式代入①,并整理,得x -2x-3=0 ④
方程④的根的判别式△=(-2) -4×1×(-3)=16>0,
所以,方程④有两个不相等的实数根x ,x , 把x ,x
分别代入方程③,得到v ,y ·
因此圆C 与圆C 有两个公共点A(x ,y ),B(x ,y ), 这两个圆相交.
试 判 断 圆C 与圆C 的 位 置 关 系 .
解法1:将圆与圆的方程联立,得到方程组
例 5 已 知 圆C :x +y +2x+8y-8=0, 圆 C :x +y -4x-4y-2=0,
典例分析
问 题3: 画 出 圆C 与 圆C 以及方程③表示的直线,你发现了什么
并求出圆C 与 圆C 的交点坐标 .
圆C :x +y +2x+8y-8=0,
圆C :x +y -4x-4y-2=0,
x+2y-1=0.③
解 :两相交圆方程相减得公共弦方程
将③式代入①,并整理,得x -2x-3=0.④
解得:x =-1,x =3. 代入
得 y =1,y =-1. 点A(-1,1),B(3,-1)
当两圆相交时,两圆方程相减,
可得两圆公共弦所在直线的方程.
典例分析
试判断圆C 与圆C 的位置关系.
解法2:把圆C 的方程化成标准方程,得(x+1) +(y+4) =25, 圆C 的圆心是(-1,-4),半径r =5.
把圆C 的方程化成标准方程,得(x-2) +(y-2) =10,
圆C 的圆心是(2,2),半径r = √ 10,
圆C 与圆C 的连心线的长为
√ (-1-2) +(-4-2) =3 √5,
圆C 与圆C 的两半径之和ri+r =5+ √ 10,
两半径之差ri-r =5-√ 10.
因为5- √ 10<3 √5<5+ √ 10,即ri-r <3√5所以圆C 与圆C 相交,它们有两个公共点A,B.
典例分析
例5已知圆C :x +y +2x+8y-8=0, 圆C :x +y -4x-4y-2=0,
思考
问题4:如果两圆方程联立消元后得到的方程的△=0,它说明什么 你 能据此确定两圆是内切还是外切吗 如何判断两圆是内切还是外切呢 当△<0时,两圆是什么位置关系
当△=0时,方程组只有一组解,此时两圆相切,但不能确定两圆是内切还是外切.
还要根据两圆的半径与圆心距作进一步判断.
当△<0 时,方程组没有解,此时两圆相离,但不能确定两圆是外离还是内含.
若0≤ d<|R-rl , 则两圆内含.
若d=IR-rl , 则两圆内切;
若d>R+r , 则两圆外离;
若d=R+r , 则两圆外切;
例6已知圆O的直径AB=4, 动 点M与点A的距离是它与点B的距离的2倍。试探 究点M 的轨迹,并判断该轨迹与圆O的位置关系
我们解以麵图辨亲适数线段事的单橋吞为療鴛灌量每牲的角坐称轨
迹紊程由A 面得到点M 的轨迹;通过研究它的轨迹方程与圆0方程的关系
判断这个轨迹与圆Q的位置关系 M
设点M 的坐标为(x,y),由TMAl= √21MB4, 得
√(x+2) +y =√2×√(x-2) +y .
化简,得x +y -12x+4=0, 即(x-6) +y =
所以点M 的轨迹是以P(6,0)为圆心,半 A
径为4 √2的一个圆.
因为两圆的圆心距为|PO|=6, 两圆的半径分别为r =2,r
又r -r把 √2倍改为k倍,该
如何分析解决这个问题
x
4×2,
解:把 圆C 方程化成标准方程,得 (x-4) +(y-3) =9.
则C (0,0),C (4,3),r =2,r =3.
∴|C C =5,ri+r =5,
∴|C C =r +r .
∴圆C 与圆C 外切.
1.已知圆C :x +y = 4,圆C :x +y -8x-6y+16=0, 判断圆C 与圆C 的位置关系。
变式训练
1.判断圆和圆的位置关系——几何法、代数法
2.圆与圆相交时的公共弦
3.满足某种几何条件的动点的轨迹——坐标法
课堂小结
1、 复习本节课内容;
2、 完成课本P98 练习题第2题;
3、 思考:圆与圆相交时的公共弦长如何求,
并求出例5两圆相交的公共弦长 .
作业
√ 0 1 | 教 材 分 析
√ 0 2 | 学 情 分 析 √ 0 3 | 目 标 分 析 √ 04 | 重点难点 05 | 教法分析
√ 06 |教学过程
《圆与圆的位置关系》是在研究“点与圆的位置关系”和“直线与圆的位置关系”的基 础上通过类比进行研究学习的,是前面所学知识的延续;
本节课在研究“圆与圆的位置关系”时主要运用几何法,重在培养学生数形结合的数 学思想。
教材分析
学情分析
授课对象:高二学生
学生已经学习了:
●圆与圆的位置关系(初中);
●点与圆、直线与圆的位置关系及其判断方法;
●学生具备基本的数学思维和思想方法:观察、类比、归纳、概括、表达等能力。
班级情况:学生基础差、底子薄、缺乏学习的主动性,在解析几何的学习上难度较大,但渴望进步。
目标分析
知识与技能:
●理解圆与圆的五种位置关系,掌握其判断方法;
●掌握两圆相交时的公共弦问题;
过程与方法:
●培养学生用解析法观察、发现、研究和解决几何问题的能力;
情感态度价值观:
●激发学生自主探究问题的兴趣;
●学生类比能力及数形结合思想的培养。
重点难点
重点:
●圆与圆的位置关系的判定方法,两圆相交时的公共弦;
难点:
●圆与圆位置关系的研究。
教学方法
为了充分调动学生学习的积极性,本节课采用“启发式”教学法,用环环相扣的问题将探
究活动层层深入,站在学生思维的最近发展区上启发诱导。
教法分析
位置关系 相交 相切
相离
图形
交点的 个数 2个 1个
0个
d与r的 关系 0≤dd>r
教学过程
复习回顾,引入新课
直线与圆的位置关系的判断
1.几何法
位置关系 相交 相切
相离
方程组解的个数 2 1
0
交点的个数 2 1
0
△与0的关系 △>0 △=0
△<0
2.代数法
合作探究,获得新知
1.复习初中所学习圆与圆之间的位置关系;
2.类比直线与圆的位置关系的判断得到圆与圆的位置关系的判断方法;
3.思考如何去求两圆相交时的公共弦所在的直线;
4.思考用代数法求圆与圆的位置关系时有什么局限性。
教学过程
典例分析,当堂训练
1.例5 圆与圆的位置关系;
2.例5 圆与圆相交时的公共弦问题;
3.例6 动点的轨迹、圆与圆的位置关系;
4.当堂训练。
教学过程
1.知识方面:圆与圆的位置关系、两圆相交时的公共弦问题;
2.方法方面:几何法、代数法;
3.思想方面:类比推理、数形结合的思想。
课堂小结,反思提高
教学过程
布置作业,分层落实
1.复习:本节课内容;
2.巩固:课本P98练习题第2题,思考两圆相交时的公共弦长如何求。
教学过程
2.5.2圆与圆的位置关系
人教A版(2019)高中数学选择性必修一第二章2.5《直线与圆、圆与圆的位置关系》
问题: 如何判断直线与圆的位置关系
代数法:
直线与圆相交,有两个交点,可通过两
△>0 方程有两解 点坐标公式求弦长
△=0 方程有一解 直线与圆相切,有一个交点
△<0 方程有0解 直线与圆相离,无交点
复习回顾
问题: 如何判断直线与圆的位置关系
几何法:
d
复习回顾
前面我们运用直线的方程、圆的方程,研究了直线与圆的 位置关系.
现在我们类比上述研究方法,运用圆的方程,通过定量计 算研究圆与圆的位置关系.
新课导入
探究新知 圆与圆的位置关系
问题1回忆一下初中所学的知识,回忆下圆与圆的位置关系有哪些
外离 0 个 外切 1 个 相交 2 个 内切 1 个
圆与圆的位置关系有五种:外离、外切、相交、内切、内含.
随着两圆的相对 位置变化,公共 点个数又分别是 多少
内含 2个
℃
C
℃
C
C *
1.代数法:联立两者方程看是否有解.
(1)由两个圆的方程
(2)消去y(或x)得到关于x(或y)的一元二次方程;
(3)求出△;
(4)判断△的符号,得出结论:
① 方程组有两组不同实数解→ 两 圆相交
②方程组有 一组实数解 两 圆 相切
③ 方程组没有实数解 两圆相离或内含
探究新知 圆与圆的位置关系
问题2类比适用直线和圆的方程,研究直线与圆的位置关系的方 法,如何利用圆的方程,判断它们之间的位置关系
利用圆的方程判断圆与圆位置关系:
联立求解.
(2)求出两圆的圆
心坐标及半径r r ;
(3)求两圆的圆
心距d;
(4)比较d 与Ir -r I, r +r 的大小关系, 得出结论:
探 究 新知 2.几何法:判断圆心距与两圆半径的和与差的绝对值的大小关 系
设圆C 的半径为r , 圆C 的半径为r , 圆心距d, 则
d=r +r
Ir -r kd
Ir -r >d
(1)把两圆的方程 化成标准方程;
②圆和圆外切
③ 圆和圆相交
⑤ 圆和圆内含
④圆和圆内切
①圆和圆外离
d>r +r
c
① - ②,得x+2y-1=0 ③
由③,
把上式代入①,并整理,得x -2x-3=0 ④
方程④的根的判别式△=(-2) -4×1×(-3)=16>0,
所以,方程④有两个不相等的实数根x ,x , 把x ,x
分别代入方程③,得到v ,y ·
因此圆C 与圆C 有两个公共点A(x ,y ),B(x ,y ), 这两个圆相交.
试 判 断 圆C 与圆C 的 位 置 关 系 .
解法1:将圆与圆的方程联立,得到方程组
例 5 已 知 圆C :x +y +2x+8y-8=0, 圆 C :x +y -4x-4y-2=0,
典例分析
问 题3: 画 出 圆C 与 圆C 以及方程③表示的直线,你发现了什么
并求出圆C 与 圆C 的交点坐标 .
圆C :x +y +2x+8y-8=0,
圆C :x +y -4x-4y-2=0,
x+2y-1=0.③
解 :两相交圆方程相减得公共弦方程
将③式代入①,并整理,得x -2x-3=0.④
解得:x =-1,x =3. 代入
得 y =1,y =-1. 点A(-1,1),B(3,-1)
当两圆相交时,两圆方程相减,
可得两圆公共弦所在直线的方程.
典例分析
试判断圆C 与圆C 的位置关系.
解法2:把圆C 的方程化成标准方程,得(x+1) +(y+4) =25, 圆C 的圆心是(-1,-4),半径r =5.
把圆C 的方程化成标准方程,得(x-2) +(y-2) =10,
圆C 的圆心是(2,2),半径r = √ 10,
圆C 与圆C 的连心线的长为
√ (-1-2) +(-4-2) =3 √5,
圆C 与圆C 的两半径之和ri+r =5+ √ 10,
两半径之差ri-r =5-√ 10.
因为5- √ 10<3 √5<5+ √ 10,即ri-r <3√5
典例分析
例5已知圆C :x +y +2x+8y-8=0, 圆C :x +y -4x-4y-2=0,
思考
问题4:如果两圆方程联立消元后得到的方程的△=0,它说明什么 你 能据此确定两圆是内切还是外切吗 如何判断两圆是内切还是外切呢 当△<0时,两圆是什么位置关系
当△=0时,方程组只有一组解,此时两圆相切,但不能确定两圆是内切还是外切.
还要根据两圆的半径与圆心距作进一步判断.
当△<0 时,方程组没有解,此时两圆相离,但不能确定两圆是外离还是内含.
若0≤ d<|R-rl , 则两圆内含.
若d=IR-rl , 则两圆内切;
若d>R+r , 则两圆外离;
若d=R+r , 则两圆外切;
例6已知圆O的直径AB=4, 动 点M与点A的距离是它与点B的距离的2倍。试探 究点M 的轨迹,并判断该轨迹与圆O的位置关系
我们解以麵图辨亲适数线段事的单橋吞为療鴛灌量每牲的角坐称轨
迹紊程由A 面得到点M 的轨迹;通过研究它的轨迹方程与圆0方程的关系
判断这个轨迹与圆Q的位置关系 M
设点M 的坐标为(x,y),由TMAl= √21MB4, 得
√(x+2) +y =√2×√(x-2) +y .
化简,得x +y -12x+4=0, 即(x-6) +y =
所以点M 的轨迹是以P(6,0)为圆心,半 A
径为4 √2的一个圆.
因为两圆的圆心距为|PO|=6, 两圆的半径分别为r =2,r
又r -r
如何分析解决这个问题
x
4×2,
解:把 圆C 方程化成标准方程,得 (x-4) +(y-3) =9.
则C (0,0),C (4,3),r =2,r =3.
∴|C C =5,ri+r =5,
∴|C C =r +r .
∴圆C 与圆C 外切.
1.已知圆C :x +y = 4,圆C :x +y -8x-6y+16=0, 判断圆C 与圆C 的位置关系。
变式训练
1.判断圆和圆的位置关系——几何法、代数法
2.圆与圆相交时的公共弦
3.满足某种几何条件的动点的轨迹——坐标法
课堂小结
1、 复习本节课内容;
2、 完成课本P98 练习题第2题;
3、 思考:圆与圆相交时的公共弦长如何求,
并求出例5两圆相交的公共弦长 .
作业
√ 0 1 | 教 材 分 析
√ 0 2 | 学 情 分 析 √ 0 3 | 目 标 分 析 √ 04 | 重点难点 05 | 教法分析
√ 06 |教学过程
《圆与圆的位置关系》是在研究“点与圆的位置关系”和“直线与圆的位置关系”的基 础上通过类比进行研究学习的,是前面所学知识的延续;
本节课在研究“圆与圆的位置关系”时主要运用几何法,重在培养学生数形结合的数 学思想。
教材分析
学情分析
授课对象:高二学生
学生已经学习了:
●圆与圆的位置关系(初中);
●点与圆、直线与圆的位置关系及其判断方法;
●学生具备基本的数学思维和思想方法:观察、类比、归纳、概括、表达等能力。
班级情况:学生基础差、底子薄、缺乏学习的主动性,在解析几何的学习上难度较大,但渴望进步。
目标分析
知识与技能:
●理解圆与圆的五种位置关系,掌握其判断方法;
●掌握两圆相交时的公共弦问题;
过程与方法:
●培养学生用解析法观察、发现、研究和解决几何问题的能力;
情感态度价值观:
●激发学生自主探究问题的兴趣;
●学生类比能力及数形结合思想的培养。
重点难点
重点:
●圆与圆的位置关系的判定方法,两圆相交时的公共弦;
难点:
●圆与圆位置关系的研究。
教学方法
为了充分调动学生学习的积极性,本节课采用“启发式”教学法,用环环相扣的问题将探
究活动层层深入,站在学生思维的最近发展区上启发诱导。
教法分析
位置关系 相交 相切
相离
图形
交点的 个数 2个 1个
0个
d与r的 关系 0≤d
教学过程
复习回顾,引入新课
直线与圆的位置关系的判断
1.几何法
位置关系 相交 相切
相离
方程组解的个数 2 1
0
交点的个数 2 1
0
△与0的关系 △>0 △=0
△<0
2.代数法
合作探究,获得新知
1.复习初中所学习圆与圆之间的位置关系;
2.类比直线与圆的位置关系的判断得到圆与圆的位置关系的判断方法;
3.思考如何去求两圆相交时的公共弦所在的直线;
4.思考用代数法求圆与圆的位置关系时有什么局限性。
教学过程
典例分析,当堂训练
1.例5 圆与圆的位置关系;
2.例5 圆与圆相交时的公共弦问题;
3.例6 动点的轨迹、圆与圆的位置关系;
4.当堂训练。
教学过程
1.知识方面:圆与圆的位置关系、两圆相交时的公共弦问题;
2.方法方面:几何法、代数法;
3.思想方面:类比推理、数形结合的思想。
课堂小结,反思提高
教学过程
布置作业,分层落实
1.复习:本节课内容;
2.巩固:课本P98练习题第2题,思考两圆相交时的公共弦长如何求。
教学过程
