新教材高中数学人教A版选择性必修一 优质课件 抛物线的简单几何性质(第1课时)(共39张PPT)
文档属性
| 名称 | 新教材高中数学人教A版选择性必修一 优质课件 抛物线的简单几何性质(第1课时)(共39张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-06 20:47:18 | ||
图片预览







文档简介
(共39张PPT)
人教A版2019选修第一册
第3章圆锥曲线的方程
3.3.2抛物线的简单几何性质
(第1课时)
01求抛物线标准方程
02求焦点弦长
目 录
学习目标
1.掌握抛物线的简单几何性质.
2.归纳、对比四种方程所表示的抛物线的
几何性质的异同.
3.掌握直线与抛物线位置关系的判断。
1.抛物线的定义
平面内与一个定点F 和一条定直线/(1不经
过点月的距离相等的点的轨迹叫做抛物线.
+—+ —n ⊥L 山 l 心 白hH+
定直线1叫做抛物线的准线
定义告诉我们:
(1)判断抛物线的一种方法
(2)抛物线上任一点的性质:| MF| =d
知识回顾
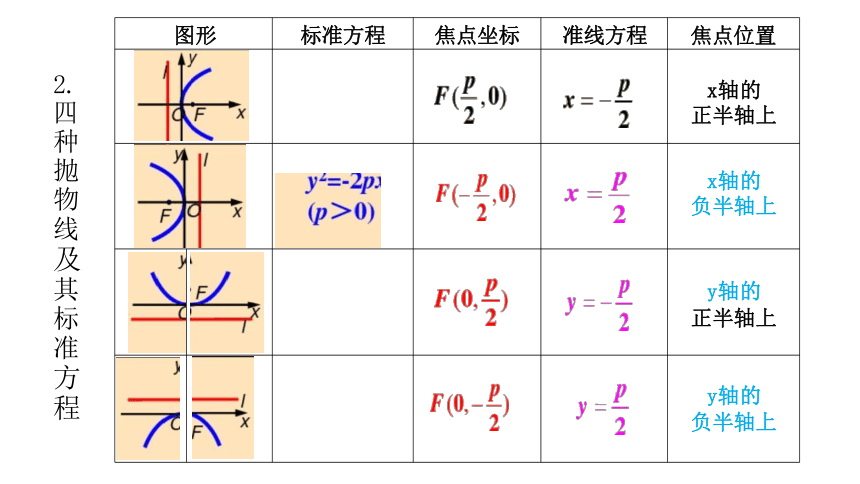
图形 标准方程 焦点坐标 准线方程
焦点位置
x轴的 正半轴上
x轴的
负半轴上
y轴的
正半轴上
y轴的
负半轴上
2. 四 种 抛 物 线 及 其 标 准 方 程
1.范围
由抛物线y =2px(p>0)
如何研究抛物线y =2px(p>0)的几何性质
所以抛物线的范围为x≥0,y∈R
新知探究
x≥0
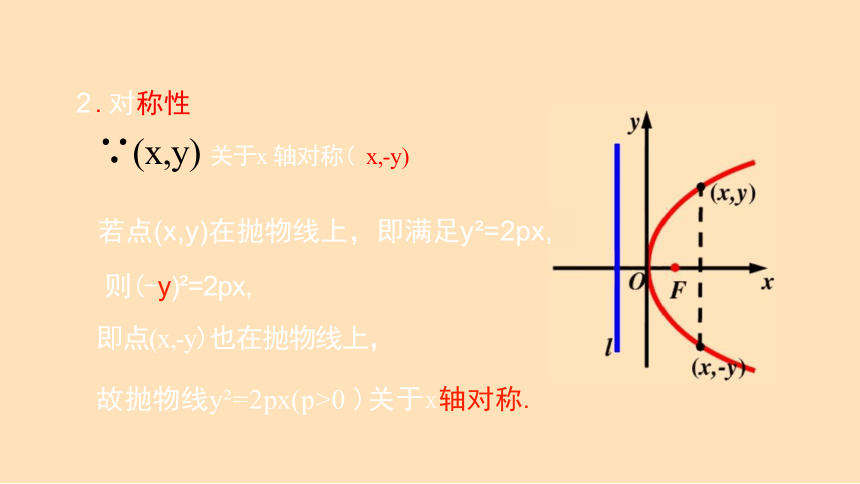
2 .对称性
∵(x,y) 关于x 轴对称( x,-y)
若点(x,y)在抛物线上,即满足y =2px,
则(-y) =2px,
即点(x,-y)也在抛物线上,
故抛物线y =2px(p>0 )关于x轴对称.
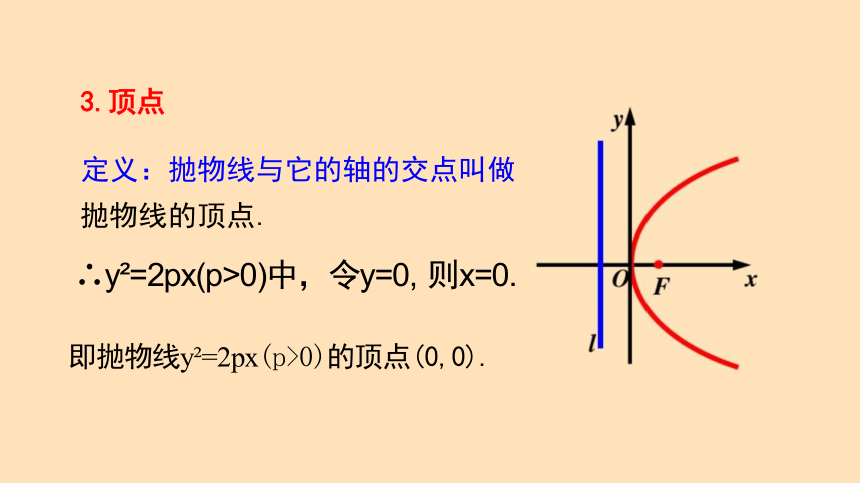
3.顶点
定义:抛物线与它的轴的交点叫做
抛物线的顶点.
∴y =2px(p>0)中,令y=0, 则x=0.
即抛物线y =2px(p>0)的顶点(0,0).
4.离心率
抛物线上的点M 与焦点F 的距
离和它到准线的距离d 之比
叫做抛物线的离心率,用e表示.
由定义知,抛物线y
乙 p p 么 」 O 一 十 —
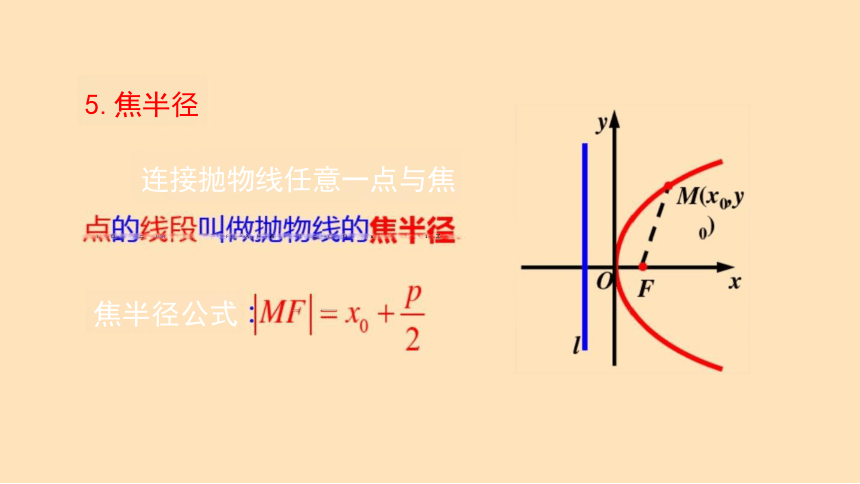
5.焦半径
连接抛物线任意一点与焦
焦半径公式
i 口 二 X+XH F 入 J 四 1 二 X 口 n 1 工
。
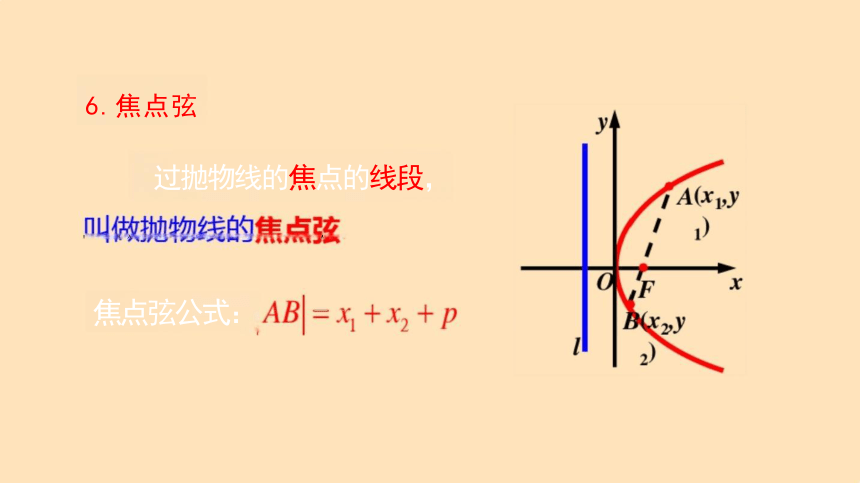
6.焦点弦
过抛物线的焦点的线段,
H H 入 X A
焦点弦公式:
7.通径
过焦点而垂直于对称轴
的弦AB,称为抛物线的通 径 . AB|=2p
个 J/12= HJJ 人 is 1—HJr
端点可较准确画出反映抛物线基本特
征的草图.
2p越大,抛物线张口越大
方程 y =2px y =-2px x =2py
x =-2py
图形
范围 x≥0,y∈R x≤0,y∈R x∈R,y≥0
x∈R,y≤0
对称性 关于x轴对称 关于y轴对称
顶点 (0,0)
焦半径
焦点弦 x +x +p +p y +y + p
-(y p
通径 2p
抛物线的简单几何性质
1.求抛物线标准方程
已知抛物线关于x轴对称,它的顶点在坐标原点,并且经过点M(2,-2√2),求它的标准方程.
解:由已知可设抛物线的标准方程为y =2px(p>0)
则将M点代入得(-2 √ 2) =2p×2 解 得:p=2
因此所求方程为:y =4x
变 式 :顶点在坐标原点,对称轴是坐标轴,并且过点M(2,-2√2) 的抛物线有几条,求它的标准方程,
y =4x或x =-√2y
解惑提高 当焦点在x轴上,开口方向不定时,设为y =2mx(m≠0),
当焦点在y轴上,开口方向不定时,设为x =2my (m≠0),可避免讨论.
典例1
练一练
1 .设抛物线y=mx (m≠0)的准线与直线y=1的距离为3,求抛物线的标准方程.
错解:由y=mx (m≠0) 可知其准线方程为
由题意知 ,解得m=8,
故所求抛物线的标准方程为y=8x .
错因分析本题在解答过程中容易出现两个错误:一是不能正确理解抛物线 标准方程的形式,错误地将所给方程看成是抛物线的标准方程,得到准线方 程为 ;
二是得到准线方程后,只分析其中的一种情况,而忽略了另一种情况,只得到 了一个解.
正解:y=mx (m≠0)可化为 ,其准线方程为
或 ,
解得 或
故所求抛物线的标准方程为 x =8y或 x =-16y.
由题意知-
2.求焦点弦长
斜率为1的直线经过抛物线y =4x的焦点F, 且与抛物线相交于两点A、B, 求焦点弦长AB 的 长 .
解:方法一:由抛物线的标准方程可知,抛物线焦点的坐标为F(1,0),
所以直线AB 的方程为y-0=1-(x-1), 即y=x-1, ①
将方程①代入抛物线方程y =4x, 化简得x -6x+1=0,
解这个方程,得x =3+2 √2,x =3-2 √2,
将x =3+2 √2,x =3-2 √2 代入方程①中,
得y =2+2 √2,y =2-2 √2,即A(3+2 √2,2+2 √2),B(3-2 √2,2-2 √2),
∴IAB-√4√2) +(4√2) =8.
典例2
解 :方法二:设A(x ,y ),B(X ,y ),
直线的为y =x-2,代入抛物线方程,得 x -6x+1=0
∴x +x =6,x X =1
∴ADeI=√ 1+k .√(x +x ) -4x X
= √ 1+12· √6 -4×1=8.
斜率为1的直线经过抛物线 y =4x的焦点F, 且与抛物线相交于两点A、B,求焦点弦长AB的长 .
典例2
如图,设A (x ,y ),B(x ,y ),A,B 两点到准线的距离分别为dA,dg.
由抛物线的定义,可知|AF|=dA=x +1,|BF|=dB=x +1,
于是|AB|=|AFI+|BF|=x +x +2.
因为直线的斜率为1,且过焦点F(1,0),
所以直线的方程为y=x-1.①
将①代入方程y =4x, 得(x-1) =4x, 化简,得x -6x+1=0.
所以x +x =6,|AB|=x +x +2=8. 所以,线段AB的长是8.
斜率为1的直线经过抛物线 y =4x的焦点F, 且与抛物线相交于两点A、B, 求焦点弦长AB的长
,焦点F的坐标为(1,0),准线方程为x=-1.
典例2
解:方法三:由题意可知,p=2,
直线和抛物线的位置关系有三种:相交、相切、相离
将直线方程和抛物线方程联立,消元转化为关于x ( 或y 的 )
方程组:
Ax +Bx+C=0 (或Ay +By+C=0), 其中A,B,C 为常数.
若A=0, 则直线和抛物线相交(直线与抛物线的对称轴平行),有一个交点;
若A≠0, 计算判别式△=B —4AC:
若△>0,则直线和抛物线相交(有两个交点);
若△=0,则直线和抛物线相切(有一个交点);
若△<0,则直线和抛物线相离(无交点).
归纳总结
练一练
2.(1)过定点 P(0,1)作与抛物线 y =2x 只有一个公共点的直线有几
条
(2)若直线l:y=(a+1)x-1 与曲线C:y =ax(a≠0) 恰好有一个公共
点,试求实数a 的取值集合.
[思路探究] (1)分斜率存在、不存在两种情况,存在时将直线方程代
入抛物线方程,转化为△=0求解;不存在时显然满足题意.
(2)将直线方程与抛物线方程联立 → 消去y后化为关于x的方程
分类讨论方程有一解时a 的取值
[解] ( 1)当直线的斜率不存在时,直线x=0, 符合题意.
当直线的斜率存在时,设过点P 的直线方程为y=kx+1, 当 k=0 时,
直线l 的方程为y=1, 满足直线与抛物线y =2x 仅有一个公共点; 当k≠0 时,将直线方程y=kx+1 代入y =2x, 消 去y 得 k x +2(k—
1)x+1=0. 由△=0,得 直线方程为 故满足条件的直
线有三条.
(2)因为直线 l 与曲线 C 恰好有一个公共点,所以方程组
只有一组实数解,消去y, 得[(a+1)x-1] =ax, 即(a+1) x -(3a+2)x+1=0 ①.
(i) 当 a+1=0, 即 a=—1 时,方程①是关于x 的一元一次方程,解
得x=—1, 这时,原方程组有唯一解
(ii) 当a+1≠0, 即 a≠-1 时,方程①是关于x 的一元二次方程.
令△=(3a+2) -4(a+1) =a(5a+4)=0, 解得a=0 (舍去)或
所以原方程组有唯一解
综上,实数a 的取值集合
课本练习
1.求适合下列条件的抛物线的标准方程:
(1)关于x轴对称,并且经过点M(5,-4);
(2)关于y 轴对称,准线经过点E(5,-5); x =20y
(3)准线在y轴右侧,顶点到准线的距离是4; y =-16x
(4)焦点F 在y轴负半轴上,经过横坐标为16的点P, 且FP平行于准线. x =-32y
3.过点M(2,0)作斜率为1的直线l,交抛物线y =4x于两点A、B, 求焦点,求AB|.
解 :设A(x ,y ),B(x V ),
直线l为y=x-2, 代入抛物线方程,得x -8x+4=0,
∴x +x =8,x X =4
∴|AB|=√ 1+k ·√(x +x ) -4x X
= √ 1+1 · √8 -4×4=4 √6.
随堂检测
1.已知抛物线 x =2py(p>0)的准线经过点(-1,-1),则抛物线的焦点坐标为(D) A.(-1,0) B.(0,-1) C.(1,0) D.(0,1)
2.已知点P(6,y)在抛物线y =2px(p>0)上,若点p到抛物线焦点F 的距离等于8,则焦点F 到抛物
线准线的距离等于( C)
A.2 B.1 C.4 D.8
3.已知抛物线y =2px(p>0)的准线与圆(x-3) +y =16 相切,则p的值为(C )
A B.1 C.2 D.4
4.抛物线x =8y 焦点为F, 准线为1,P 为抛物线上一点,PA⊥l,A 为垂足,如果直线AF的倾 斜角等于60°,那么|PF|等于(C )
A.2√3 B.4√3 C. D.3
5.—条光线从抛物线y =2px(p>0)的焦点F射出,经抛物线上一点B 反射后,反射光线经过点 A(5,4),若 |AB|+|FB|=6,则抛物线的标准方程为 y =4x.
【解析】抛物线具有光学性质,即从焦点出发的光经抛物线上一点反射后,反射光线沿平行于抛物
所以 , 即p=2. 所以抛物线的标准方程为y =4x.
线对称轴的方向射出.
设B(m,4), ,则|AB=5-m,
事
3
6.若抛物线y =2x上的一点M到坐标原点O的距离为√3,则点M到该抛物线焦点的距离为_ 2
【解析】设点 ∵MO|=3,∴ ∴:y =2或y =-6(舍去),∴
∴M到抛物线 y =2x的准线 的距离
∵点M到抛物线焦点的距离等于点M到抛物线 y =2x的准线的距离,
∴点M到该抛物线焦点的距离为
7.已知抛物线y =8x.
(1)求出该抛物线的顶点、焦点、准线方程、对称轴、变量x的范围;
(2)以坐标原点0为顶点,作抛物线的内接等腰三角形OAB,IOAI=IOBI,若焦点
F 是△OAB的重心,求△OAB的周长 .
解:(1)抛物线y =8x的顶点、焦点、准线方程、对称轴、变量x的范围分别为(0,0),(2,0),x=-2,x轴,x≥0.
因为F(2,0),
所以 ,所以M(30) 故设A(3,m),
代入 y =8x 得m =24,
所以m=2 √6 或m=-2 √6,
所以A(3,2 √6),B(3,-2 √6),
所以IOAl=IOBI= √33,
所以△OAB的周长为2√33+4 √6.
(2)如图所示,由lOAl=IOBl可知AB⊥x轴,垂足为点M,
又焦点F 是△OAB的重心,
8. 已知点P(1,m) 是抛物线C:y =2px 上的点,F 为抛物线的焦点,
且|PF|=2, 直线l:y=k(x-1) 与抛物线C 相交于不同的两点A,B.
(1)求抛物线C 的方程;
(2)若|AB|=8, 求 k 的值.
[解]( 1)抛物线C:y =2px 的准线为
由|PF|=2 得 : 得p=2.
所以抛物线的方程为y =4x.
35
可得k x —(2k +4)x+k =0,△=16k +16>0,
解得k=±1, 所 以k的值为1或—1.
∵直线l 经过抛物线C 的焦点F,
(2)设A(x1,y1),B(x ,y2),
由
9.设P 是抛物线y =4x 上的一个动点,F 为抛物线的焦点.
(1)若点P 到直线x=-1 的距离为d,A(-1,1), 求 |PA|+d 的最小值;
( 2 ) 若B(3,2),求 |PB|+|PFI的最小值.
【解】(1)依题意,抛物线的焦点为F(1,0), 准线方程为x=-1.
由已知及抛物线的定义,可知|PF=d, 于是问题转化为求|PA|+|PF| 的最小值.
由平面几何知识知,当F,P,A 三点共线时, |PA|+|PF| 取得最小值, 最小值为|AF F=√5,即 |PA|+d的最小值为√5.
(2)把点B 的横坐标代入y =4x中,得y=±2√3,
因为2 √3>2,所以点B 在抛物线的内部.
过B 作BQ 垂直准线于点Q, 交抛物线于点P (如图所示) .
由抛物线的定义,可知|PQ|=|PF, 则|PB|+|PF|≥|PB|+|PQ|=BQ=3+1=4,
所以|PB|+|PF| 的最小值为4.
1.掌握抛物线的几何性质:
范围、对称性、顶点、离心率、焦半径、通径;
2.会利用抛物线的几何性质求抛物线的标准方程、焦点坐标及解决其它问题.
课堂小结
1I
THANKS
II
人教A版2019选修第一册
第3章圆锥曲线的方程
3.3.2抛物线的简单几何性质
(第1课时)
01求抛物线标准方程
02求焦点弦长
目 录
学习目标
1.掌握抛物线的简单几何性质.
2.归纳、对比四种方程所表示的抛物线的
几何性质的异同.
3.掌握直线与抛物线位置关系的判断。
1.抛物线的定义
平面内与一个定点F 和一条定直线/(1不经
过点月的距离相等的点的轨迹叫做抛物线.
+—+ —n ⊥L 山 l 心 白hH+
定直线1叫做抛物线的准线
定义告诉我们:
(1)判断抛物线的一种方法
(2)抛物线上任一点的性质:| MF| =d
知识回顾
图形 标准方程 焦点坐标 准线方程
焦点位置
x轴的 正半轴上
x轴的
负半轴上
y轴的
正半轴上
y轴的
负半轴上
2. 四 种 抛 物 线 及 其 标 准 方 程
1.范围
由抛物线y =2px(p>0)
如何研究抛物线y =2px(p>0)的几何性质
所以抛物线的范围为x≥0,y∈R
新知探究
x≥0
2 .对称性
∵(x,y) 关于x 轴对称( x,-y)
若点(x,y)在抛物线上,即满足y =2px,
则(-y) =2px,
即点(x,-y)也在抛物线上,
故抛物线y =2px(p>0 )关于x轴对称.
3.顶点
定义:抛物线与它的轴的交点叫做
抛物线的顶点.
∴y =2px(p>0)中,令y=0, 则x=0.
即抛物线y =2px(p>0)的顶点(0,0).
4.离心率
抛物线上的点M 与焦点F 的距
离和它到准线的距离d 之比
叫做抛物线的离心率,用e表示.
由定义知,抛物线y
乙 p p 么 」 O 一 十 —
5.焦半径
连接抛物线任意一点与焦
焦半径公式
i 口 二 X+XH F 入 J 四 1 二 X 口 n 1 工
。
6.焦点弦
过抛物线的焦点的线段,
H H 入 X A
焦点弦公式:
7.通径
过焦点而垂直于对称轴
的弦AB,称为抛物线的通 径 . AB|=2p
个 J/12= HJJ 人 is 1—HJr
端点可较准确画出反映抛物线基本特
征的草图.
2p越大,抛物线张口越大
方程 y =2px y =-2px x =2py
x =-2py
图形
范围 x≥0,y∈R x≤0,y∈R x∈R,y≥0
x∈R,y≤0
对称性 关于x轴对称 关于y轴对称
顶点 (0,0)
焦半径
焦点弦 x +x +p +p y +y + p
-(y p
通径 2p
抛物线的简单几何性质
1.求抛物线标准方程
已知抛物线关于x轴对称,它的顶点在坐标原点,并且经过点M(2,-2√2),求它的标准方程.
解:由已知可设抛物线的标准方程为y =2px(p>0)
则将M点代入得(-2 √ 2) =2p×2 解 得:p=2
因此所求方程为:y =4x
变 式 :顶点在坐标原点,对称轴是坐标轴,并且过点M(2,-2√2) 的抛物线有几条,求它的标准方程,
y =4x或x =-√2y
解惑提高 当焦点在x轴上,开口方向不定时,设为y =2mx(m≠0),
当焦点在y轴上,开口方向不定时,设为x =2my (m≠0),可避免讨论.
典例1
练一练
1 .设抛物线y=mx (m≠0)的准线与直线y=1的距离为3,求抛物线的标准方程.
错解:由y=mx (m≠0) 可知其准线方程为
由题意知 ,解得m=8,
故所求抛物线的标准方程为y=8x .
错因分析本题在解答过程中容易出现两个错误:一是不能正确理解抛物线 标准方程的形式,错误地将所给方程看成是抛物线的标准方程,得到准线方 程为 ;
二是得到准线方程后,只分析其中的一种情况,而忽略了另一种情况,只得到 了一个解.
正解:y=mx (m≠0)可化为 ,其准线方程为
或 ,
解得 或
故所求抛物线的标准方程为 x =8y或 x =-16y.
由题意知-
2.求焦点弦长
斜率为1的直线经过抛物线y =4x的焦点F, 且与抛物线相交于两点A、B, 求焦点弦长AB 的 长 .
解:方法一:由抛物线的标准方程可知,抛物线焦点的坐标为F(1,0),
所以直线AB 的方程为y-0=1-(x-1), 即y=x-1, ①
将方程①代入抛物线方程y =4x, 化简得x -6x+1=0,
解这个方程,得x =3+2 √2,x =3-2 √2,
将x =3+2 √2,x =3-2 √2 代入方程①中,
得y =2+2 √2,y =2-2 √2,即A(3+2 √2,2+2 √2),B(3-2 √2,2-2 √2),
∴IAB-√4√2) +(4√2) =8.
典例2
解 :方法二:设A(x ,y ),B(X ,y ),
直线的为y =x-2,代入抛物线方程,得 x -6x+1=0
∴x +x =6,x X =1
∴ADeI=√ 1+k .√(x +x ) -4x X
= √ 1+12· √6 -4×1=8.
斜率为1的直线经过抛物线 y =4x的焦点F, 且与抛物线相交于两点A、B,求焦点弦长AB的长 .
典例2
如图,设A (x ,y ),B(x ,y ),A,B 两点到准线的距离分别为dA,dg.
由抛物线的定义,可知|AF|=dA=x +1,|BF|=dB=x +1,
于是|AB|=|AFI+|BF|=x +x +2.
因为直线的斜率为1,且过焦点F(1,0),
所以直线的方程为y=x-1.①
将①代入方程y =4x, 得(x-1) =4x, 化简,得x -6x+1=0.
所以x +x =6,|AB|=x +x +2=8. 所以,线段AB的长是8.
斜率为1的直线经过抛物线 y =4x的焦点F, 且与抛物线相交于两点A、B, 求焦点弦长AB的长
,焦点F的坐标为(1,0),准线方程为x=-1.
典例2
解:方法三:由题意可知,p=2,
直线和抛物线的位置关系有三种:相交、相切、相离
将直线方程和抛物线方程联立,消元转化为关于x ( 或y 的 )
方程组:
Ax +Bx+C=0 (或Ay +By+C=0), 其中A,B,C 为常数.
若A=0, 则直线和抛物线相交(直线与抛物线的对称轴平行),有一个交点;
若A≠0, 计算判别式△=B —4AC:
若△>0,则直线和抛物线相交(有两个交点);
若△=0,则直线和抛物线相切(有一个交点);
若△<0,则直线和抛物线相离(无交点).
归纳总结
练一练
2.(1)过定点 P(0,1)作与抛物线 y =2x 只有一个公共点的直线有几
条
(2)若直线l:y=(a+1)x-1 与曲线C:y =ax(a≠0) 恰好有一个公共
点,试求实数a 的取值集合.
[思路探究] (1)分斜率存在、不存在两种情况,存在时将直线方程代
入抛物线方程,转化为△=0求解;不存在时显然满足题意.
(2)将直线方程与抛物线方程联立 → 消去y后化为关于x的方程
分类讨论方程有一解时a 的取值
[解] ( 1)当直线的斜率不存在时,直线x=0, 符合题意.
当直线的斜率存在时,设过点P 的直线方程为y=kx+1, 当 k=0 时,
直线l 的方程为y=1, 满足直线与抛物线y =2x 仅有一个公共点; 当k≠0 时,将直线方程y=kx+1 代入y =2x, 消 去y 得 k x +2(k—
1)x+1=0. 由△=0,得 直线方程为 故满足条件的直
线有三条.
(2)因为直线 l 与曲线 C 恰好有一个公共点,所以方程组
只有一组实数解,消去y, 得[(a+1)x-1] =ax, 即(a+1) x -(3a+2)x+1=0 ①.
(i) 当 a+1=0, 即 a=—1 时,方程①是关于x 的一元一次方程,解
得x=—1, 这时,原方程组有唯一解
(ii) 当a+1≠0, 即 a≠-1 时,方程①是关于x 的一元二次方程.
令△=(3a+2) -4(a+1) =a(5a+4)=0, 解得a=0 (舍去)或
所以原方程组有唯一解
综上,实数a 的取值集合
课本练习
1.求适合下列条件的抛物线的标准方程:
(1)关于x轴对称,并且经过点M(5,-4);
(2)关于y 轴对称,准线经过点E(5,-5); x =20y
(3)准线在y轴右侧,顶点到准线的距离是4; y =-16x
(4)焦点F 在y轴负半轴上,经过横坐标为16的点P, 且FP平行于准线. x =-32y
3.过点M(2,0)作斜率为1的直线l,交抛物线y =4x于两点A、B, 求焦点,求AB|.
解 :设A(x ,y ),B(x V ),
直线l为y=x-2, 代入抛物线方程,得x -8x+4=0,
∴x +x =8,x X =4
∴|AB|=√ 1+k ·√(x +x ) -4x X
= √ 1+1 · √8 -4×4=4 √6.
随堂检测
1.已知抛物线 x =2py(p>0)的准线经过点(-1,-1),则抛物线的焦点坐标为(D) A.(-1,0) B.(0,-1) C.(1,0) D.(0,1)
2.已知点P(6,y)在抛物线y =2px(p>0)上,若点p到抛物线焦点F 的距离等于8,则焦点F 到抛物
线准线的距离等于( C)
A.2 B.1 C.4 D.8
3.已知抛物线y =2px(p>0)的准线与圆(x-3) +y =16 相切,则p的值为(C )
A B.1 C.2 D.4
4.抛物线x =8y 焦点为F, 准线为1,P 为抛物线上一点,PA⊥l,A 为垂足,如果直线AF的倾 斜角等于60°,那么|PF|等于(C )
A.2√3 B.4√3 C. D.3
5.—条光线从抛物线y =2px(p>0)的焦点F射出,经抛物线上一点B 反射后,反射光线经过点 A(5,4),若 |AB|+|FB|=6,则抛物线的标准方程为 y =4x.
【解析】抛物线具有光学性质,即从焦点出发的光经抛物线上一点反射后,反射光线沿平行于抛物
所以 , 即p=2. 所以抛物线的标准方程为y =4x.
线对称轴的方向射出.
设B(m,4), ,则|AB=5-m,
事
3
6.若抛物线y =2x上的一点M到坐标原点O的距离为√3,则点M到该抛物线焦点的距离为_ 2
【解析】设点 ∵MO|=3,∴ ∴:y =2或y =-6(舍去),∴
∴M到抛物线 y =2x的准线 的距离
∵点M到抛物线焦点的距离等于点M到抛物线 y =2x的准线的距离,
∴点M到该抛物线焦点的距离为
7.已知抛物线y =8x.
(1)求出该抛物线的顶点、焦点、准线方程、对称轴、变量x的范围;
(2)以坐标原点0为顶点,作抛物线的内接等腰三角形OAB,IOAI=IOBI,若焦点
F 是△OAB的重心,求△OAB的周长 .
解:(1)抛物线y =8x的顶点、焦点、准线方程、对称轴、变量x的范围分别为(0,0),(2,0),x=-2,x轴,x≥0.
因为F(2,0),
所以 ,所以M(30) 故设A(3,m),
代入 y =8x 得m =24,
所以m=2 √6 或m=-2 √6,
所以A(3,2 √6),B(3,-2 √6),
所以IOAl=IOBI= √33,
所以△OAB的周长为2√33+4 √6.
(2)如图所示,由lOAl=IOBl可知AB⊥x轴,垂足为点M,
又焦点F 是△OAB的重心,
8. 已知点P(1,m) 是抛物线C:y =2px 上的点,F 为抛物线的焦点,
且|PF|=2, 直线l:y=k(x-1) 与抛物线C 相交于不同的两点A,B.
(1)求抛物线C 的方程;
(2)若|AB|=8, 求 k 的值.
[解]( 1)抛物线C:y =2px 的准线为
由|PF|=2 得 : 得p=2.
所以抛物线的方程为y =4x.
35
可得k x —(2k +4)x+k =0,△=16k +16>0,
解得k=±1, 所 以k的值为1或—1.
∵直线l 经过抛物线C 的焦点F,
(2)设A(x1,y1),B(x ,y2),
由
9.设P 是抛物线y =4x 上的一个动点,F 为抛物线的焦点.
(1)若点P 到直线x=-1 的距离为d,A(-1,1), 求 |PA|+d 的最小值;
( 2 ) 若B(3,2),求 |PB|+|PFI的最小值.
【解】(1)依题意,抛物线的焦点为F(1,0), 准线方程为x=-1.
由已知及抛物线的定义,可知|PF=d, 于是问题转化为求|PA|+|PF| 的最小值.
由平面几何知识知,当F,P,A 三点共线时, |PA|+|PF| 取得最小值, 最小值为|AF F=√5,即 |PA|+d的最小值为√5.
(2)把点B 的横坐标代入y =4x中,得y=±2√3,
因为2 √3>2,所以点B 在抛物线的内部.
过B 作BQ 垂直准线于点Q, 交抛物线于点P (如图所示) .
由抛物线的定义,可知|PQ|=|PF, 则|PB|+|PF|≥|PB|+|PQ|=BQ=3+1=4,
所以|PB|+|PF| 的最小值为4.
1.掌握抛物线的几何性质:
范围、对称性、顶点、离心率、焦半径、通径;
2.会利用抛物线的几何性质求抛物线的标准方程、焦点坐标及解决其它问题.
课堂小结
1I
THANKS
II
