2.5 圆与圆的位置关系 课件(共26张PPT)-人教A版高中数学选择性必修第一册
文档属性
| 名称 | 2.5 圆与圆的位置关系 课件(共26张PPT)-人教A版高中数学选择性必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 434.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-06 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
人教2019 A版选择性必修一
第二章 直线和圆的方程
2.5.2圆与圆的位置关系
1.掌握圆与圆的位置关系及判定方法.
2.能根据圆的方程判断圆与圆的位置关系
3.能综合应用圆与圆的位置关系解决问题
新教材
情景导学
日食是一种天文现象,在民间
称此现象为天狗食日。日食只在
月球与太阳呈现合的状态时发生。
日食分为日偏食、日全食、日环
食、全环食。
我们将月亮与太阳抽象为圆,观
察到的这些圆在变化的过程中位
置关系是怎样的
新教材
前面我们运用直线的方程,圆的方程研究了直线与圆的位置
关系,现在我们类比上述研究方法,运用圆的方程,通过定量计算 研究圆与圆的位置关系。
问题思考
新教材
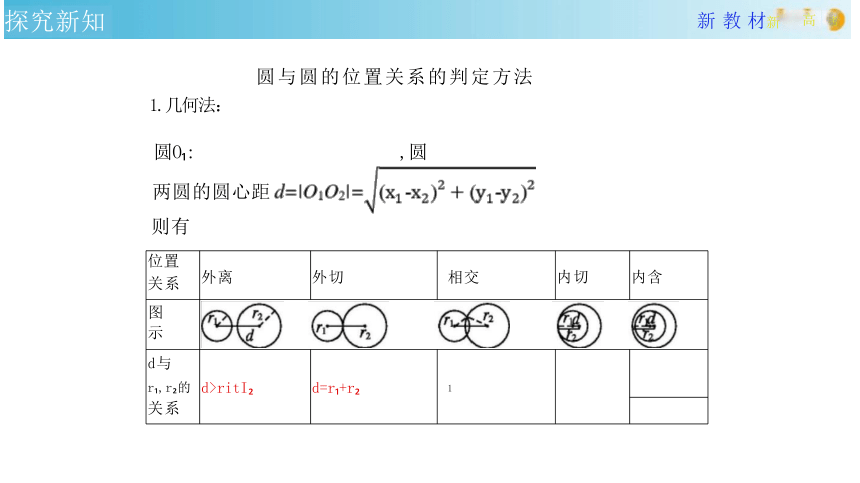
位置 关系 外离 外切 相交 内切
内含
图 示
d与 r ,r 的 关系 d>ritI d=r +r 1
圆与圆的位置关系的判定方法
1.几何法:
圆O : ,圆
两圆的圆心距
则有
探究新知
新 教 材新
高 考
新教材 新
2.代数法:圆O :x +y +D x+E y+F =0(D +E -4F >0), 圆
O :x +y +D x+E y+F =0(D +E2-4F >0), 两圆的方程联立得方程 组,则有
方程组解的情况 2组 1组
0组
两圆的公共点 2个 1个
0个
两圆的位置关系 相交 外切或内切
外离或内含
新教材新高 考
1.判断下列两圆的位置关系:
①(x+2) +(y-2) =1与(x-2) +(y-5) =16.
②x +y +6x-7=0与x +y +6y-27=0.
解:①根据题意得,两圆的半径分别为r =1和r =4,两圆的圆心距
因为d=r +r ,所以两圆外切.
②将两圆的方程化为标准方程,得(x+3) +y =16,x +(y+3) =36, 故两圆的半径分别为r =4和r =6.
两圆的圆心距
d=J[o-(-3)] +(-3-O) =3√Z,因为Ir1-r I例1 已知圆C :x +y -2ax-2y+a -15=0(a>0),圆C :x +y -4ax-2y+4a =0(a>0).试求a为何值
时,两圆C ,C 的位置关系为:
(1)相切;
(2)相交;
(3)外离;
(4)内含
典例解析
思路分析:求出圆心距,与两半径的和或差比较求出a的值.
新教材 新
(1)当IC C I =r +r =5,即a=5时,两圆外切;
当IC C I=r -r =3,即a=3时,两圆内切.
(2)当3(3)当IC C I>5,即a>5 时,两圆外离.
(4)当IC C I<3,即0解:圆C ,C 的方程,经配方后可得 C :(x-a) +(y-1) =16,
C :(x-2a) +(y-1) =1,
∴圆心C (a,1),C (2a,1),半径r =4,r =1.
新 教 材 新高
判断两圆的位置关系的两种方法
(1)几何法:利用两圆半径的和或差与圆心距作比较,得到两圆的位置关系;
(2)代数法:把两圆位置关系的判定完全转化为代数问题,转化为方程组的解
的组数问题.
归纳总结
新教材
跟踪训练 新教材 新
跟踪训练1若两圆x +y =a与x +y +6x-8y-11=0内切,则a的值为
解析::x +y =a表示一个圆, .∴a>0.
两圆的圆心、半径长分别为(0,0), √a与(-3,4),6.
由于两圆内切,则
解得a=121 或a=1.
答 案:121或1
典例解析 新 教 材新
例2已知圆C :x +y +6x-4=0 和圆C :x +y +6y-28=0.
(1)求两圆公共弦所在直线的方程及弦长;
(2)求经过两圆交点且圆心在直线x-y-4=0 上的圆的方程.
思路分析:(1)两圆方程相减求出公共弦所在直线方程,再根据半径、弦心距、 弦长的关系求出弦长.
(2)可求出两圆的交点坐标,结合圆心在直线x-y-4=0上求出圆心坐标与半径, 也可利用圆系方程求解.
解:(1)设两圆交点为A (x1,y ),B(x ,y ),则A,B 两点坐标是方程组
的解 .
①-②,得x-y+4=0.
A,B 两点坐标都满足此方程,
.x-y+4=0 即为两圆公共弦所在直线的方程.
又圆C 的圆心(-3,0),r= √ 13,
新 教 材 新
即两圆的公共弦长为5 √2.
C 到直线AB的距离为
(2)(方法1)解方程
得两圆的交点A(-1,3),B(-6,-2).
设所求圆的圆心为(a,b),因圆心在直线x-y-4=0上,故b=a-4.
则
解得 故圆心为 ,半径为
故圆的方程为
即x +y -x+7y-32=0.
(方法2)设所求圆的方程为x +y +6x-4+λ(x +y +6y-28)=0(λ≠-1), 其圆心为 ,代入x-y-4=0,解得λ=-7.
故所求圆的方程为x +y -x+7y-32=0.
新教材新高
相交弦及圆系方程问题的解决
1.求两圆的公共弦所在直线的方程的方法:将两圆方程相减即得两圆公共弦
所在直线方程,但必须注意只有当两圆方程中二次项系数相同时,才能如此求 解,否则应先调整系数.
2.求两圆公共弦长的方法: 一是联立两圆方程求出交点坐标,再用距离公式求
解;二是先求出两圆公共弦所在的直线方程,再利用半径长、弦心距和弦长的 一半构成的直角三角形求解.
3.已知圆C :x +y +D x+E y+F =0 与圆C :x +y +D x+E y+F =0 相交,则过两
圆交点的圆的方程可设为x +y +D x+E y+F +λ(x +y +D x+E y+F )=0(λ≠-1).
新教材 新 高
归纳总结
解析:由题意知直线AB 与直线x-y+c=0 垂直, ∴kAB×1=-1.
即 ,得m=5,
.AB 的中点坐标为(3,1).
AB的中点在直线x-y+c=0上,
. ∴3-1+c=0,.c=-2,
.m+c=5-2=3.
跟踪训练1两圆相交于两点A(1,3)和B(m,-1),两圆圆心都在直线x-y+c=0上,则
值为
跟踪训练
新教材 新
答案:3
的
典例解析
例 3求与圆x +y -2x=0外切且与直线x+ √3y=0相切于点M(3,-√3) 的圆的方程.
思路分析:设圆的方程,利用两圆外切和直线与圆相切建立方程组求得.
解:设所求圆的方程为(x-a) +(y-b) =r (r>0),
由题知所求圆与圆x +y -2x=0外切,
则
又所求圆过点M的切线为直线x+√3y=0,
故
解由①②③组成的方程组得a=4,b=0,r=2或a=0,b=-4 √3,r=6. 故所求圆的方程为(x-4) +y =4或x +(y+4 √3) =36.
新教材新
变式探究1将本例变为“求与圆x +y -2x=0外切,圆心在x轴上,且过
点(3,- √3)的圆的方程”,如何求
解:因为圆心在x轴上,
所以可设圆心坐标为(a,0),设半径为r,
则所求圆的方程为(x-a) +y =r ,
又因为与圆x +y -2x=0外切,且过点(3,-√3),
所以
解得
所以圆的方程为(x-4) +y =4.
新教材新
变式探究2将本例改为“若圆x +y -2x=0与圆x +y -8x-8y+m=0相外切”,试
求实数m的值.
解:圆x +y -2x=0的圆心为A(1,0),半径为r =1,
圆x +y -8x-8y+m=0的圆心为B(4,4),
半径为r = √32-m.因为两圆相外切,
所 以(4-1) +(4-0) =1+ √32-m,解得m=16.
新教材 新
处理两圆相切问题的两个步骤
(1)定性,即必须准确把握是内切还是外切,若只是告诉相切,则必须考
虑分两圆内切还是外切两种情况讨论.
(2)转化思想,即将两圆相切的问题转化为两圆的圆心距等于两圆半径
之差的绝对值(内切时)或两圆半径之和(外切时).
归纳总结 新教材
解析:圆x +y -1=0表示以O (0,0)点为圆心,以R =1 为半径的圆.
圆x +y -4x+2y-4=0表示以O (2,-1)点为圆心,以R =3为半径的圆
:10 O I=√5,
∴R -R <10 0 I∴圆x +y -1=0和圆x +y -4x+2y-4=0相交.
答案:B
新 教 材 新高
1.两圆x +y -1=0和x +y -4x+2y-4=0的位置关系是( )
A.内切 B. 相交 C.外切 D.外离
当堂检测
考
2.圆C :x +y -12x-2y-13=0和圆C :x +y +12x+16y-25=0的公共弦所在的直
线方程是
新 教 材 新
解析:两圆的方程相减得公共弦所在的直线方程为4x+3y-2=0.
答案:4x+3y-2=0
3.半径为6的圆与x轴相切,且与圆x +(y-3) =1内切,则此圆的方程为( )
A.(x-4) +(y-6) =16
B.(x±4) +(y-6) =16
C.(x-4) +(y-6) =36
D.(x±4) +(y-6) =36
解析:设所求圆心坐标为(a,b),则Ibl=6.由题意,得a +(b-3) =(6-1) =25.
若b=6,则a=±4;若b=-6,则a无解.故所求圆方程为(x±4) +(y-6) =36.
答案:D
新 教 材 新高 考
4.若圆C :x +y =4与圆C,:x +y -2ax+a -1=0内切,则a等于
解析:圆C 的圆心C (0,0),半径r =2.
圆C 可化为(x-a) +y =1,即圆心C (a,0),半径r =1,若两圆内切,需
IC C I=√a +0 =2-1=1. 解得a=±1.
答案:±1
新教材新 考
新教材新高考
5.已知两个圆C :x +y =4,C :x +y -2x-4y+4=0,直线l:x+2y=0,求经过C 和C 的交点且和l相 切的圆的方程.
解:设所求圆的方程为x +y +4-2x-4y+λ(x +y -4)=0,即
(1+λ)x +(1+λ)y -2x-4y+4(1-λ)=0.所以圆心为
半径为
解得λ=±1,舍去λ=-1,圆x +y =4显然不符合题意,故所求圆的方程 为x +y -x-2y=0.
外离:
外切:
相交: T
内切:
内含:
圆与圆的位置关系: 圆O
新 教 材 新
人教2019 A版选择性必修一
第二章 直线和圆的方程
2.5.2圆与圆的位置关系
1.掌握圆与圆的位置关系及判定方法.
2.能根据圆的方程判断圆与圆的位置关系
3.能综合应用圆与圆的位置关系解决问题
新教材
情景导学
日食是一种天文现象,在民间
称此现象为天狗食日。日食只在
月球与太阳呈现合的状态时发生。
日食分为日偏食、日全食、日环
食、全环食。
我们将月亮与太阳抽象为圆,观
察到的这些圆在变化的过程中位
置关系是怎样的
新教材
前面我们运用直线的方程,圆的方程研究了直线与圆的位置
关系,现在我们类比上述研究方法,运用圆的方程,通过定量计算 研究圆与圆的位置关系。
问题思考
新教材
位置 关系 外离 外切 相交 内切
内含
图 示
d与 r ,r 的 关系 d>ritI d=r +r 1
圆与圆的位置关系的判定方法
1.几何法:
圆O : ,圆
两圆的圆心距
则有
探究新知
新 教 材新
高 考
新教材 新
2.代数法:圆O :x +y +D x+E y+F =0(D +E -4F >0), 圆
O :x +y +D x+E y+F =0(D +E2-4F >0), 两圆的方程联立得方程 组,则有
方程组解的情况 2组 1组
0组
两圆的公共点 2个 1个
0个
两圆的位置关系 相交 外切或内切
外离或内含
新教材新高 考
1.判断下列两圆的位置关系:
①(x+2) +(y-2) =1与(x-2) +(y-5) =16.
②x +y +6x-7=0与x +y +6y-27=0.
解:①根据题意得,两圆的半径分别为r =1和r =4,两圆的圆心距
因为d=r +r ,所以两圆外切.
②将两圆的方程化为标准方程,得(x+3) +y =16,x +(y+3) =36, 故两圆的半径分别为r =4和r =6.
两圆的圆心距
d=J[o-(-3)] +(-3-O) =3√Z,因为Ir1-r I
时,两圆C ,C 的位置关系为:
(1)相切;
(2)相交;
(3)外离;
(4)内含
典例解析
思路分析:求出圆心距,与两半径的和或差比较求出a的值.
新教材 新
(1)当IC C I =r +r =5,即a=5时,两圆外切;
当IC C I=r -r =3,即a=3时,两圆内切.
(2)当3
(4)当IC C I<3,即0
C :(x-2a) +(y-1) =1,
∴圆心C (a,1),C (2a,1),半径r =4,r =1.
新 教 材 新高
判断两圆的位置关系的两种方法
(1)几何法:利用两圆半径的和或差与圆心距作比较,得到两圆的位置关系;
(2)代数法:把两圆位置关系的判定完全转化为代数问题,转化为方程组的解
的组数问题.
归纳总结
新教材
跟踪训练 新教材 新
跟踪训练1若两圆x +y =a与x +y +6x-8y-11=0内切,则a的值为
解析::x +y =a表示一个圆, .∴a>0.
两圆的圆心、半径长分别为(0,0), √a与(-3,4),6.
由于两圆内切,则
解得a=121 或a=1.
答 案:121或1
典例解析 新 教 材新
例2已知圆C :x +y +6x-4=0 和圆C :x +y +6y-28=0.
(1)求两圆公共弦所在直线的方程及弦长;
(2)求经过两圆交点且圆心在直线x-y-4=0 上的圆的方程.
思路分析:(1)两圆方程相减求出公共弦所在直线方程,再根据半径、弦心距、 弦长的关系求出弦长.
(2)可求出两圆的交点坐标,结合圆心在直线x-y-4=0上求出圆心坐标与半径, 也可利用圆系方程求解.
解:(1)设两圆交点为A (x1,y ),B(x ,y ),则A,B 两点坐标是方程组
的解 .
①-②,得x-y+4=0.
A,B 两点坐标都满足此方程,
.x-y+4=0 即为两圆公共弦所在直线的方程.
又圆C 的圆心(-3,0),r= √ 13,
新 教 材 新
即两圆的公共弦长为5 √2.
C 到直线AB的距离为
(2)(方法1)解方程
得两圆的交点A(-1,3),B(-6,-2).
设所求圆的圆心为(a,b),因圆心在直线x-y-4=0上,故b=a-4.
则
解得 故圆心为 ,半径为
故圆的方程为
即x +y -x+7y-32=0.
(方法2)设所求圆的方程为x +y +6x-4+λ(x +y +6y-28)=0(λ≠-1), 其圆心为 ,代入x-y-4=0,解得λ=-7.
故所求圆的方程为x +y -x+7y-32=0.
新教材新高
相交弦及圆系方程问题的解决
1.求两圆的公共弦所在直线的方程的方法:将两圆方程相减即得两圆公共弦
所在直线方程,但必须注意只有当两圆方程中二次项系数相同时,才能如此求 解,否则应先调整系数.
2.求两圆公共弦长的方法: 一是联立两圆方程求出交点坐标,再用距离公式求
解;二是先求出两圆公共弦所在的直线方程,再利用半径长、弦心距和弦长的 一半构成的直角三角形求解.
3.已知圆C :x +y +D x+E y+F =0 与圆C :x +y +D x+E y+F =0 相交,则过两
圆交点的圆的方程可设为x +y +D x+E y+F +λ(x +y +D x+E y+F )=0(λ≠-1).
新教材 新 高
归纳总结
解析:由题意知直线AB 与直线x-y+c=0 垂直, ∴kAB×1=-1.
即 ,得m=5,
.AB 的中点坐标为(3,1).
AB的中点在直线x-y+c=0上,
. ∴3-1+c=0,.c=-2,
.m+c=5-2=3.
跟踪训练1两圆相交于两点A(1,3)和B(m,-1),两圆圆心都在直线x-y+c=0上,则
值为
跟踪训练
新教材 新
答案:3
的
典例解析
例 3求与圆x +y -2x=0外切且与直线x+ √3y=0相切于点M(3,-√3) 的圆的方程.
思路分析:设圆的方程,利用两圆外切和直线与圆相切建立方程组求得.
解:设所求圆的方程为(x-a) +(y-b) =r (r>0),
由题知所求圆与圆x +y -2x=0外切,
则
又所求圆过点M的切线为直线x+√3y=0,
故
解由①②③组成的方程组得a=4,b=0,r=2或a=0,b=-4 √3,r=6. 故所求圆的方程为(x-4) +y =4或x +(y+4 √3) =36.
新教材新
变式探究1将本例变为“求与圆x +y -2x=0外切,圆心在x轴上,且过
点(3,- √3)的圆的方程”,如何求
解:因为圆心在x轴上,
所以可设圆心坐标为(a,0),设半径为r,
则所求圆的方程为(x-a) +y =r ,
又因为与圆x +y -2x=0外切,且过点(3,-√3),
所以
解得
所以圆的方程为(x-4) +y =4.
新教材新
变式探究2将本例改为“若圆x +y -2x=0与圆x +y -8x-8y+m=0相外切”,试
求实数m的值.
解:圆x +y -2x=0的圆心为A(1,0),半径为r =1,
圆x +y -8x-8y+m=0的圆心为B(4,4),
半径为r = √32-m.因为两圆相外切,
所 以(4-1) +(4-0) =1+ √32-m,解得m=16.
新教材 新
处理两圆相切问题的两个步骤
(1)定性,即必须准确把握是内切还是外切,若只是告诉相切,则必须考
虑分两圆内切还是外切两种情况讨论.
(2)转化思想,即将两圆相切的问题转化为两圆的圆心距等于两圆半径
之差的绝对值(内切时)或两圆半径之和(外切时).
归纳总结 新教材
解析:圆x +y -1=0表示以O (0,0)点为圆心,以R =1 为半径的圆.
圆x +y -4x+2y-4=0表示以O (2,-1)点为圆心,以R =3为半径的圆
:10 O I=√5,
∴R -R <10 0 I
答案:B
新 教 材 新高
1.两圆x +y -1=0和x +y -4x+2y-4=0的位置关系是( )
A.内切 B. 相交 C.外切 D.外离
当堂检测
考
2.圆C :x +y -12x-2y-13=0和圆C :x +y +12x+16y-25=0的公共弦所在的直
线方程是
新 教 材 新
解析:两圆的方程相减得公共弦所在的直线方程为4x+3y-2=0.
答案:4x+3y-2=0
3.半径为6的圆与x轴相切,且与圆x +(y-3) =1内切,则此圆的方程为( )
A.(x-4) +(y-6) =16
B.(x±4) +(y-6) =16
C.(x-4) +(y-6) =36
D.(x±4) +(y-6) =36
解析:设所求圆心坐标为(a,b),则Ibl=6.由题意,得a +(b-3) =(6-1) =25.
若b=6,则a=±4;若b=-6,则a无解.故所求圆方程为(x±4) +(y-6) =36.
答案:D
新 教 材 新高 考
4.若圆C :x +y =4与圆C,:x +y -2ax+a -1=0内切,则a等于
解析:圆C 的圆心C (0,0),半径r =2.
圆C 可化为(x-a) +y =1,即圆心C (a,0),半径r =1,若两圆内切,需
IC C I=√a +0 =2-1=1. 解得a=±1.
答案:±1
新教材新 考
新教材新高考
5.已知两个圆C :x +y =4,C :x +y -2x-4y+4=0,直线l:x+2y=0,求经过C 和C 的交点且和l相 切的圆的方程.
解:设所求圆的方程为x +y +4-2x-4y+λ(x +y -4)=0,即
(1+λ)x +(1+λ)y -2x-4y+4(1-λ)=0.所以圆心为
半径为
解得λ=±1,舍去λ=-1,圆x +y =4显然不符合题意,故所求圆的方程 为x +y -x-2y=0.
外离:
外切:
相交: T
内切:
内含:
圆与圆的位置关系: 圆O
新 教 材 新
