2.2.2 直线的两点式方程-【新教材】人教A版(2019)高中数学选择性必修第一册课件(共43张PPT)
文档属性
| 名称 | 2.2.2 直线的两点式方程-【新教材】人教A版(2019)高中数学选择性必修第一册课件(共43张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-07 09:33:41 | ||
图片预览











文档简介
(共38张PPT)
第二章直线和圆的方程
2.2 直线的方程
2.2.2 直线的两点式方程
学 习 目 标
核 心 素 养
1.掌握直线方程两点式的形式、 特点及适用范围.(重点) 2.了解直线方程截距式的形式、 特点及适用范围.(重点) 3.会用中点坐标公式求两点的 中点坐标.
1.通过直线两点式方程的推导,提
升逻辑推理的数学素养.
2.通过直线的两点式方程和截距
式方程的学习,培养直观想象和数 学运算的数学素养.
情境引入·助学助教
某区商业中心0有通往东、西、南、北的四条大街,某公园位
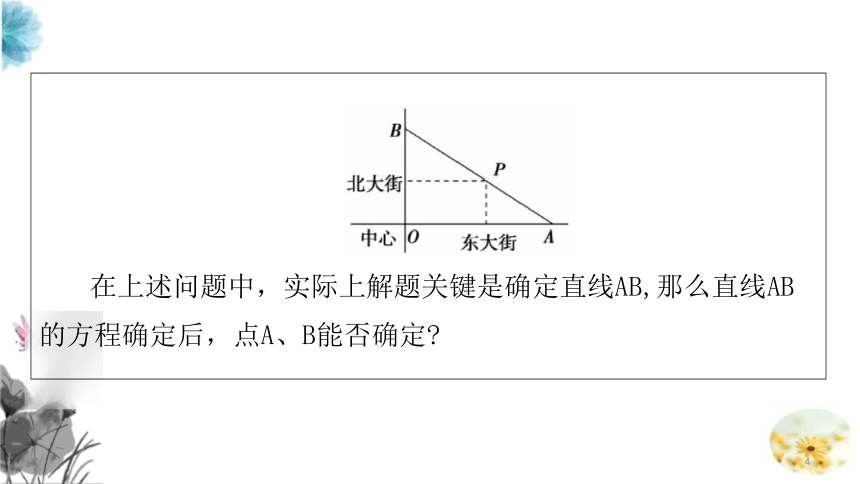
于东大街北侧、北大街东 P 处,如图所示.公园到东大街、北大街 的垂直距离分别为1 km 和4 km. 现在要在公园前修建一条直线大道 分别与东大街、北大街交汇于A、B 两处,并使区商业中心O 到 A、 B 两处的距离之和最短.
在上述问题中,实际上解题关键是确定直线AB,那么直线AB
的方程确定后,点A、B能否确定
名称 两点式方程
截距式方程
已知条件 其中 X
在x轴、y轴上的截距分别为
a、b,且a≠0,b≠0.
示意图 y P 0 P x
y
(0,b)
(a,0) x
新知初探
1. 直线的两点式和截距式方程
0
名称 两点式方程
截距式方程
直线方程 ) Y x 一 X X2—X
=1
适用范围 斜率存在且不为零
斜率存在且不为零,不过原点
思考:方 和方程(y-y )(x —x )=(x—x )(v -y )
的适用范围相同吗
[提示] 不同.前者为分式形式方程,它不表示垂直于坐标轴的
直线,后者为整式形式方程,它表示过任何两点的直线.
2. 线段的中点坐标公式
若点P ,P 的坐标分别为(x ,y ),(x ,y ),
设 P(x,y) 是线段
P P 的中点,则
初试身手一
1. 思考辨析( 正确的打“ √ ”,错误的打“×”)
(1)直线的两点式方程也可以
示 . ( )
(2)任何直线都可以用方 表示 . ( )
(3)能用两点式写出的直线方程,也可以用点斜式方程写出.
[提示] (1)× (2)×(3) √
( )
2 . 过点A(3,2),B(4,3) 的直线方程是( )
A.x+y+1=0 B.x+y-1=0
C.x—y+1=0 D.x—y-1=0
D [由直线的两点式方程,
化简,得x—y—1=
x=2 [因为两点的横坐标相等,都是2,所以直线方程是x=2.]
3. 若直线l经过点A(2,5),B(2,7),则直线l的方程为 .
[令y=0 得 即在x 轴上的截距为
4 . 直 线y=3x+2 在 x 轴上的截距是
密
.
类 型 1 直线的两点式方程
【 例 1】 (1)若直线l 经过点A(2,—1),B(2,7), 则直线l 的方
(2)若点 P(3,m) 在过点 A(2,—1),B (一3,4)的直线上,则 m=
程为
.
l 没有两点式方程,所求的直线方程为x=2.
(2)由直线方程的两点式
∴直线AB的方程为y +1=—x+2,
∵点P(3,m) 在直线AB 上,
则m+1=—3+2, 得 m=—2.]
(1)x=2 (2)-2 [(1)由于点A 与 点B 的横坐标相等,所以直线
规律方法
由两点式求直线方程的步骤
(1)设出直线所经过点的坐标.
(2)根据题中的条件,找到有关方程,解出点的坐标.
(3)由直线的两点式方程写出直线的方程.
提醒:当已知两点坐标,求过这两点的直线方程时,首先要判断
是否满足两点式方程的适用条件:两点的连线不垂直于坐标轴.若满
足,则考虑用两点式求方程.
规律方法
1. 求经过两点A(2,m) 和B(n,3)的直线方程.
[解] 当 m=3 时,直线垂直于y 轴,方程为y=3,
当n=2 时,直线垂直于x 轴,方程为x=2.
当m≠3 且 n≠2 时,由两点式得
直线方程
[跟进训练]
【 例 2】 求过点(4,—3)且在两坐标轴上截距相等的直线l 的
方程.
类 型 2 直线的截距式方程
截距相等为0
截距相等不为0
[思路探究]
设方 程求
解
截距 相等
①当a≠0,b≠0 时,设l 的方程
∵点(4,—3)在直线上,
若a=b, 则 a=b=1, 直线方程为x +y—1=0.
②当a=b=0 时,直线过原点,且过点(4,一3),
∴直线的方程为3x+4y=0.
综上知,所求直线方程为x+y-1=0 或 3x+4y=0.
[解] 设直线在x 轴、y 轴上的截距分别为a,b.
[母题探究]
1. [变条件] 本例中把“截距相等”改为“截距互为相反数”,
求直线l 的方程.
[解] 当截距均为零时,设直线方程为y=kx, 把点(4,- 3)代入
得 — 3=4k, 解 得 所求的直线方程为 即 3x
当截距均不为零且相反时,可设直线方程
—3)代入 解得a=7, 所求直线方程
—y—7=0,
故所求l 的方程为x—y-7=0 或 3x+4y=0.
把点(4,
即x
2. [变条件] 本例中把“相等”改为“绝对值相等呢 ”
[解] 当直线在两轴上的截距的绝对值相等时,包括:
①两截距均为零,即3x+4y=0
②两截距均不为零且相等即x+y-1=0.
③两截距均不为零且相反即x—y-7=0.
故所求的直线方程为x—y-7=0 或 x+y-1=0 或 3x+4y=0.
●规律方法 0 0
利用截距式求直线方程的注意事项
(1)用截距式求直线方程时,纵截距和横截距都必须存在且都不为0.
①若a=0,b≠0, 则直线方程为x=0;
②若a≠0,b= 0,则直线方程为y=0;
③若a=0,b =0, 则直线方程为y=kx(k≠0).
(2)截距相等且不为零,可设x +y=a;
截距相反且不为零,可设x—y=a;
截距相等且均为零,可设y=kx.
[探究问题]
1.若已知直线过定点,选择什么形式较好 过两点呢
[提示] 点斜式.若直线过两定点可选择两点式或点斜式.
类 型 3 直线方程的灵活应用
2. 若已知直线的斜率,选哪种形式的方程
[提示] 可选择斜截式.
3. 若已知直线与两坐标轴相交,选哪种形式的方程较好
[提示] 选择截距式较好.
[思路探究] ( 1)B,C 两点坐标两点式求方程
(2)求中点坐标两点式求直线方程
【例3】 已知A(—3,2),B(5,—4),C(0,
(1)求BC 边的方程;
(2)求BC 边上的中线所在直线的方程.
一2),在△ABC中,
[解] (1)BC 边过两点B(5,-4),C(O, 一2),
由两点式,得 即 2x+5y+10=0,
故 BC 边的方程是2x+5y +10=0(0≤x≤5).
所 以BC 边上的中线所在直线的方程为10x+11y+8=0.
又BC 边的中线过点A(一3,2),
(2)设BC 的中点为M(a,b),
即10x+11y+8=0,
所以
则
力
4
又高线过点C(0, 一2),
∴由点斜式方程得高线所在直线方程为
即 4x—3y-6=0.
1. 本例中条件不变,试求AB 边上的高线所在直线的方程.
[解] 设AB 边上的高线所在直线斜率为k,
[母题探究]
··
[解] 由 探 究 1 知 即中位线所在直线斜率为
例题知BC 的中点
所以由点斜式方程可得,中位线所在直线方程为
即 6x十 +9=0.
2. 本例中条件不变,试求与AB 平行的中位线所在直线的方程.
由
争
规律方法
直线方程的选择技巧
(1)已知一点的坐标,求过该点的直线方程, 一般选取点斜式方
程,再由其他条件确定直线的斜率.
(2)若已知直线的斜率, 一般选用直线的斜截式,再由其他条件
确定直线的一个点或者截距.
(3)若已知两点坐标, 一般选用直线的两点式方程,若两点是与
坐标轴的交点,就用截距式方程.
(4)不论选用怎样的直线方程,都要注意各自方程的限制条件,
对特殊情况下的直线要单独讨论解决.
规律方法
它的方程,此时直线的方程分别是 x=x 和 y=y ,
而它们都适合(x —x )(y—y )=(y —y )(x—x ),即两点式的整式形式,
因此过任意两点的直线的方程都可以写成(x —x )(y—yi)=(y —y )(x
x )的形式.
必备素养一
1. 当直线没有斜率(x =x ) 或斜率为0(y =y ) 时,不能用两点式
2. 直线的截距式是两点式的一个特殊情形,用它来画直线以及
判断直线经过的象限或求直线与坐标轴围成的三角形的面积比较方 便.注意直线过原点或与坐标轴平行时,没有截距式方程,但直线过
原点时两截距存在且同时等于零.
学以致用一
1. 过 P (2,0),P (0,3)两点的直线方程是( )
A. B.
C. D.
C [由条件可知,直线在x 轴 、y 轴上的截距分别为2,3,所以
方程
2.过两点(一1,1)和(3,9)的直线在x 轴上的截距是 .
[由两点式 即y—1=2(x+1),令 y=0得x
所以直线在x 轴上的截距为
垂直的直线方程是 _.
的斜率是一3,所以所求直线的斜
即x—3y+16=0.]
3.经过点(一1,5),且与直
x-3y+16=0 [直
率是 4 所以所求直线方程是
的直线方程.
[解] 设直线方程的截距式
则 解得a=2 或 a=1,
则直线方程
即 2x+3y—6=0 或 x+2y-2=0.
4 . 求过点P(6, 一 2),且在x 轴上的截距比在y 轴上的截距大1
第二章直线和圆的方程
2.2 直线的方程
2.2.2 直线的两点式方程
学 习 目 标
核 心 素 养
1.掌握直线方程两点式的形式、 特点及适用范围.(重点) 2.了解直线方程截距式的形式、 特点及适用范围.(重点) 3.会用中点坐标公式求两点的 中点坐标.
1.通过直线两点式方程的推导,提
升逻辑推理的数学素养.
2.通过直线的两点式方程和截距
式方程的学习,培养直观想象和数 学运算的数学素养.
情境引入·助学助教
某区商业中心0有通往东、西、南、北的四条大街,某公园位
于东大街北侧、北大街东 P 处,如图所示.公园到东大街、北大街 的垂直距离分别为1 km 和4 km. 现在要在公园前修建一条直线大道 分别与东大街、北大街交汇于A、B 两处,并使区商业中心O 到 A、 B 两处的距离之和最短.
在上述问题中,实际上解题关键是确定直线AB,那么直线AB
的方程确定后,点A、B能否确定
名称 两点式方程
截距式方程
已知条件 其中 X
在x轴、y轴上的截距分别为
a、b,且a≠0,b≠0.
示意图 y P 0 P x
y
(0,b)
(a,0) x
新知初探
1. 直线的两点式和截距式方程
0
名称 两点式方程
截距式方程
直线方程 ) Y x 一 X X2—X
=1
适用范围 斜率存在且不为零
斜率存在且不为零,不过原点
思考:方 和方程(y-y )(x —x )=(x—x )(v -y )
的适用范围相同吗
[提示] 不同.前者为分式形式方程,它不表示垂直于坐标轴的
直线,后者为整式形式方程,它表示过任何两点的直线.
2. 线段的中点坐标公式
若点P ,P 的坐标分别为(x ,y ),(x ,y ),
设 P(x,y) 是线段
P P 的中点,则
初试身手一
1. 思考辨析( 正确的打“ √ ”,错误的打“×”)
(1)直线的两点式方程也可以
示 . ( )
(2)任何直线都可以用方 表示 . ( )
(3)能用两点式写出的直线方程,也可以用点斜式方程写出.
[提示] (1)× (2)×(3) √
( )
2 . 过点A(3,2),B(4,3) 的直线方程是( )
A.x+y+1=0 B.x+y-1=0
C.x—y+1=0 D.x—y-1=0
D [由直线的两点式方程,
化简,得x—y—1=
x=2 [因为两点的横坐标相等,都是2,所以直线方程是x=2.]
3. 若直线l经过点A(2,5),B(2,7),则直线l的方程为 .
[令y=0 得 即在x 轴上的截距为
4 . 直 线y=3x+2 在 x 轴上的截距是
密
.
类 型 1 直线的两点式方程
【 例 1】 (1)若直线l 经过点A(2,—1),B(2,7), 则直线l 的方
(2)若点 P(3,m) 在过点 A(2,—1),B (一3,4)的直线上,则 m=
程为
.
l 没有两点式方程,所求的直线方程为x=2.
(2)由直线方程的两点式
∴直线AB的方程为y +1=—x+2,
∵点P(3,m) 在直线AB 上,
则m+1=—3+2, 得 m=—2.]
(1)x=2 (2)-2 [(1)由于点A 与 点B 的横坐标相等,所以直线
规律方法
由两点式求直线方程的步骤
(1)设出直线所经过点的坐标.
(2)根据题中的条件,找到有关方程,解出点的坐标.
(3)由直线的两点式方程写出直线的方程.
提醒:当已知两点坐标,求过这两点的直线方程时,首先要判断
是否满足两点式方程的适用条件:两点的连线不垂直于坐标轴.若满
足,则考虑用两点式求方程.
规律方法
1. 求经过两点A(2,m) 和B(n,3)的直线方程.
[解] 当 m=3 时,直线垂直于y 轴,方程为y=3,
当n=2 时,直线垂直于x 轴,方程为x=2.
当m≠3 且 n≠2 时,由两点式得
直线方程
[跟进训练]
【 例 2】 求过点(4,—3)且在两坐标轴上截距相等的直线l 的
方程.
类 型 2 直线的截距式方程
截距相等为0
截距相等不为0
[思路探究]
设方 程求
解
截距 相等
①当a≠0,b≠0 时,设l 的方程
∵点(4,—3)在直线上,
若a=b, 则 a=b=1, 直线方程为x +y—1=0.
②当a=b=0 时,直线过原点,且过点(4,一3),
∴直线的方程为3x+4y=0.
综上知,所求直线方程为x+y-1=0 或 3x+4y=0.
[解] 设直线在x 轴、y 轴上的截距分别为a,b.
[母题探究]
1. [变条件] 本例中把“截距相等”改为“截距互为相反数”,
求直线l 的方程.
[解] 当截距均为零时,设直线方程为y=kx, 把点(4,- 3)代入
得 — 3=4k, 解 得 所求的直线方程为 即 3x
当截距均不为零且相反时,可设直线方程
—3)代入 解得a=7, 所求直线方程
—y—7=0,
故所求l 的方程为x—y-7=0 或 3x+4y=0.
把点(4,
即x
2. [变条件] 本例中把“相等”改为“绝对值相等呢 ”
[解] 当直线在两轴上的截距的绝对值相等时,包括:
①两截距均为零,即3x+4y=0
②两截距均不为零且相等即x+y-1=0.
③两截距均不为零且相反即x—y-7=0.
故所求的直线方程为x—y-7=0 或 x+y-1=0 或 3x+4y=0.
●规律方法 0 0
利用截距式求直线方程的注意事项
(1)用截距式求直线方程时,纵截距和横截距都必须存在且都不为0.
①若a=0,b≠0, 则直线方程为x=0;
②若a≠0,b= 0,则直线方程为y=0;
③若a=0,b =0, 则直线方程为y=kx(k≠0).
(2)截距相等且不为零,可设x +y=a;
截距相反且不为零,可设x—y=a;
截距相等且均为零,可设y=kx.
[探究问题]
1.若已知直线过定点,选择什么形式较好 过两点呢
[提示] 点斜式.若直线过两定点可选择两点式或点斜式.
类 型 3 直线方程的灵活应用
2. 若已知直线的斜率,选哪种形式的方程
[提示] 可选择斜截式.
3. 若已知直线与两坐标轴相交,选哪种形式的方程较好
[提示] 选择截距式较好.
[思路探究] ( 1)B,C 两点坐标两点式求方程
(2)求中点坐标两点式求直线方程
【例3】 已知A(—3,2),B(5,—4),C(0,
(1)求BC 边的方程;
(2)求BC 边上的中线所在直线的方程.
一2),在△ABC中,
[解] (1)BC 边过两点B(5,-4),C(O, 一2),
由两点式,得 即 2x+5y+10=0,
故 BC 边的方程是2x+5y +10=0(0≤x≤5).
所 以BC 边上的中线所在直线的方程为10x+11y+8=0.
又BC 边的中线过点A(一3,2),
(2)设BC 的中点为M(a,b),
即10x+11y+8=0,
所以
则
力
4
又高线过点C(0, 一2),
∴由点斜式方程得高线所在直线方程为
即 4x—3y-6=0.
1. 本例中条件不变,试求AB 边上的高线所在直线的方程.
[解] 设AB 边上的高线所在直线斜率为k,
[母题探究]
··
[解] 由 探 究 1 知 即中位线所在直线斜率为
例题知BC 的中点
所以由点斜式方程可得,中位线所在直线方程为
即 6x十 +9=0.
2. 本例中条件不变,试求与AB 平行的中位线所在直线的方程.
由
争
规律方法
直线方程的选择技巧
(1)已知一点的坐标,求过该点的直线方程, 一般选取点斜式方
程,再由其他条件确定直线的斜率.
(2)若已知直线的斜率, 一般选用直线的斜截式,再由其他条件
确定直线的一个点或者截距.
(3)若已知两点坐标, 一般选用直线的两点式方程,若两点是与
坐标轴的交点,就用截距式方程.
(4)不论选用怎样的直线方程,都要注意各自方程的限制条件,
对特殊情况下的直线要单独讨论解决.
规律方法
它的方程,此时直线的方程分别是 x=x 和 y=y ,
而它们都适合(x —x )(y—y )=(y —y )(x—x ),即两点式的整式形式,
因此过任意两点的直线的方程都可以写成(x —x )(y—yi)=(y —y )(x
x )的形式.
必备素养一
1. 当直线没有斜率(x =x ) 或斜率为0(y =y ) 时,不能用两点式
2. 直线的截距式是两点式的一个特殊情形,用它来画直线以及
判断直线经过的象限或求直线与坐标轴围成的三角形的面积比较方 便.注意直线过原点或与坐标轴平行时,没有截距式方程,但直线过
原点时两截距存在且同时等于零.
学以致用一
1. 过 P (2,0),P (0,3)两点的直线方程是( )
A. B.
C. D.
C [由条件可知,直线在x 轴 、y 轴上的截距分别为2,3,所以
方程
2.过两点(一1,1)和(3,9)的直线在x 轴上的截距是 .
[由两点式 即y—1=2(x+1),令 y=0得x
所以直线在x 轴上的截距为
垂直的直线方程是 _.
的斜率是一3,所以所求直线的斜
即x—3y+16=0.]
3.经过点(一1,5),且与直
x-3y+16=0 [直
率是 4 所以所求直线方程是
的直线方程.
[解] 设直线方程的截距式
则 解得a=2 或 a=1,
则直线方程
即 2x+3y—6=0 或 x+2y-2=0.
4 . 求过点P(6, 一 2),且在x 轴上的截距比在y 轴上的截距大1
