三角形全等的判定(一)
图片预览



文档简介
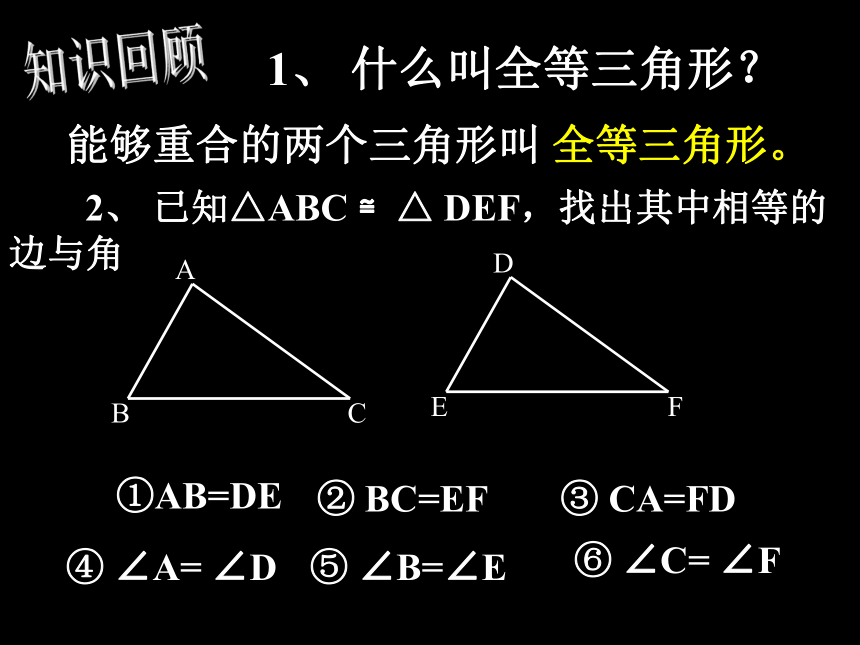
课件27张PPT。§11.2 三角形全等的判定(一)知识回顾 1、 什么叫全等三角形?能够重合的两个三角形叫 全等三角形。 2、 已知△ABC ≌△ DEF,找出其中相等的边与角①AB=DE③ CA=FD② BC=EF④ ∠A= ∠D⑤ ∠B=∠E⑥ ∠C= ∠F①AB=DE③ CA=FD② BC=EF④ ∠A= ∠D⑤ ∠B=∠E⑥ ∠C= ∠F这六个条件可以保证△ABC ≌△ DEF.
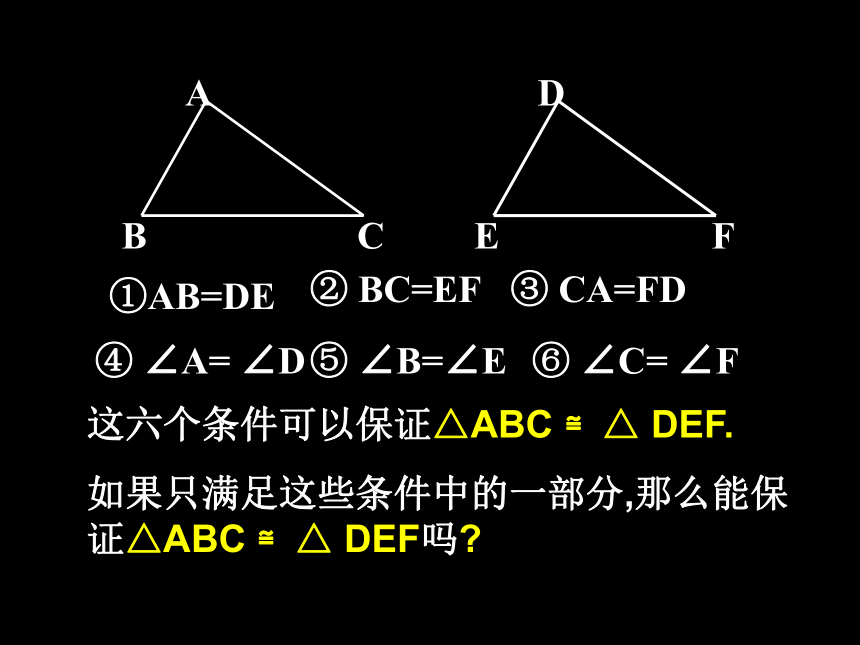
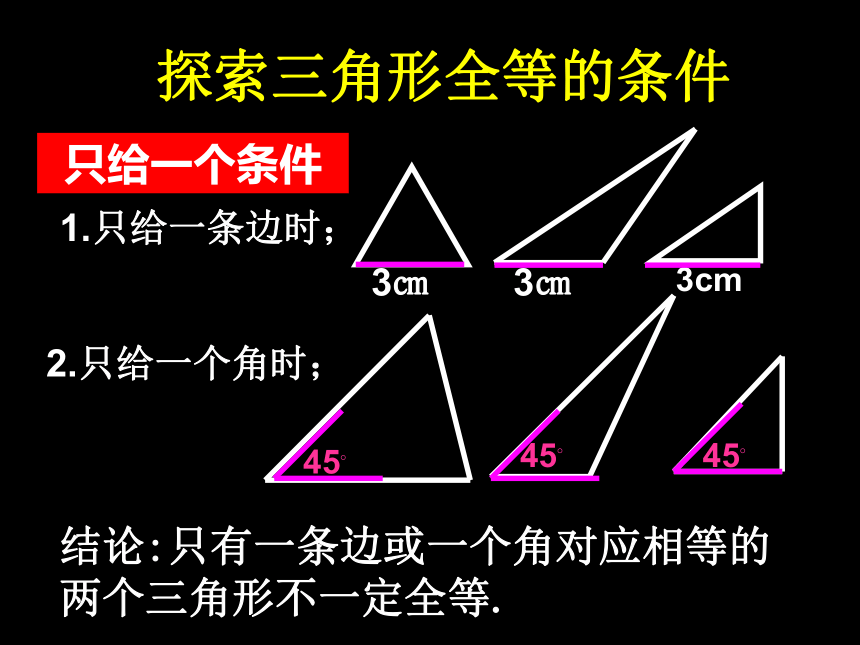
如果只满足这些条件中的一部分,那么能保证△ABC ≌△ DEF吗?探索三角形全等的条件1.只给一条边时;3㎝3㎝只给一个条件45?45?2.只给一个角时;3cm45?结论:只有一条边或一个角对应相等的两个三角形不一定全等.①两边;③两角。②一边一角;如果给出两个条件画三角形,
能有哪几种可能的情况?
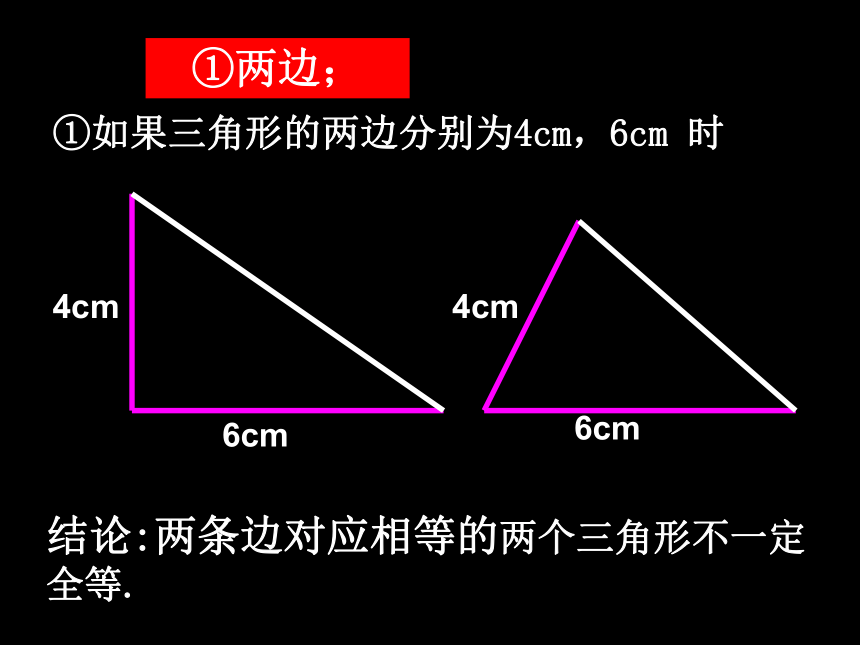
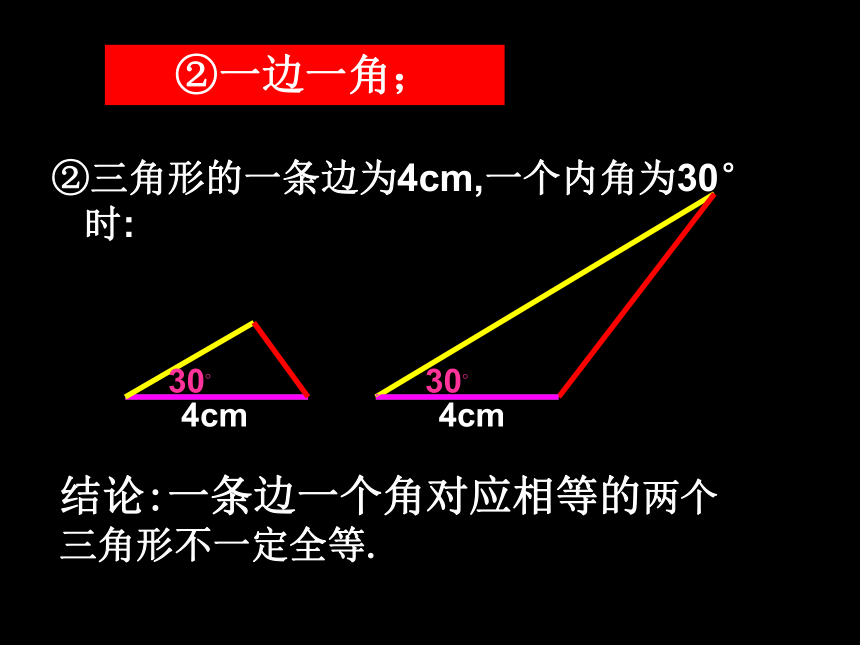
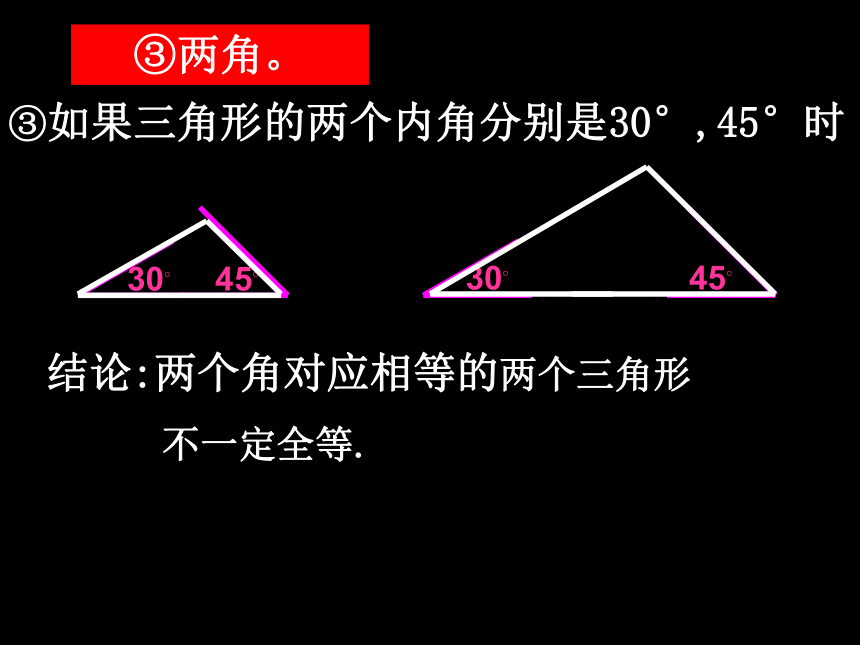
只给两个条件①如果三角形的两边分别为4cm,6cm 时6cm6cm4cm4cm结论:两条边对应相等的两个三角形不一定全等.①两边;②三角形的一条边为4cm,一个内角为30°时:4cm4cm30?30?结论:一条边一个角对应相等的两个三角形不一定全等.②一边一角;③如果三角形的两个内角分别是30°,45°时结论:两个角对应相等的两个三角形
不一定全等.③两角。结论:只给出一个或两个条件时,都不能保证所画的三角形一定全等。你能得到什么结论吗?①三角;②三边;③两边一角;④两角一边。如果给出三个条件画三角形,
你能说出有哪几种可能的情况?
①三角;--不全等②三边;如果两个三角形的三条边分别对应相等,那么这两个三角形全等吗?探究:你能画出使得AB=3cm 、 BC=4cm AC=5cm的△ABC吗?
你能画出使得AB=3cm 、 BC=5cm 、 AC=6cm的△ABC吗?A/B/C/ABC如果两个三角形的三条边分别对应相等,
那么这两个三角形全等.(S.S.S.)在△ABC与△DEF中AB=DE
AC=DF
BC=EF∴△ABC≌△DEF(SSS)判断两个三角形全等的推理过程,叫做证明三角形全等。如何用符号(数学)语言来表达呢?
例1 如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。 例题讲解答: △ABC≌△DCB
理由如下:∵ 在△ABC和△DCB中AB = CDAC = BDBC =CB∴ △ABC≌△DCB(SSS)(公共边)(已知)(已知)归纳:①准备条件:证全等时要用的间接条件要先证好有所需的直接条件;②三角形全等书写三步骤:写出在哪两个三角形中摆出三个条件用大括号括起来写出全等结论证明的书写步骤: A C B D证明:∵D是BC的中点∴BD=CD在△ABD与△ACD中AB=AC(已知)BD=CD(已证)AD=AD(公共边)∴△ABD≌△ACD(SSS)例2 如图, △ABC是一个钢架,AB=AC,AD是连接A与BC中点D的支架,求证: △ABD≌△ACD若要求证:∠B=∠C,你会吗?1 已知:如图,AB=AD,BC=CD,
求证:△ABC≌ △ADCABCDACAC ( ) ≌AB=AD ( )
BC=CD ( )∴ △ABC △ADC(SSS)证明:在△ABC和△ADC中=已知已知 公共边随堂练习: 如图,AB=AC,AE=AD,BD=CE,求证:△AEB ≌ △ ADC。证明:∵BD=CE
∴ BD-ED=CE-ED,即BE=CD。2如图,已知AB=CD,BC=DA。你能说明△ABC与△CDA全等吗?为什么? DBAC解:在△ABC与△CDA中,
∵∴△ABC≌△CDA(SSS)随堂练习:3.已知:如图,AB=AD,BC=CD,
求证:△ABC≌ △ADC4.如图,AB=CD,AC=BD,
求证: △ABC ≌ △DCB 随堂练习:5.如图,C是AB的中点,AD=CE,CD=BE,求证:△ACD≌△CBE随堂练习:6.已知,点A,D,B,F在一条直线上,AD=FB ,AC=FE,BC=DE
证明△ABC ≌△ FDE,ACBDEF随堂练习:拓展思维,才能架起知识的桥梁……7.已知:如图,AB=AC,BD=CD.你能说明∠B=∠C吗?8:如图,AB=AC,BD=CD,BH=CH,图中有几组全等的三角形?它们全等的条件是什么?HDCBA解:有三组。 在△ABH和△ACH中 ∵AB=AC,BH=CH,AH=AH ∴△ABH≌△ACH(SSS);在△ABH和△ACH中∵AB=AC,BD=CD,AD=AD ∴△ABD≌△ACD(SSS);在△ABH和△ACH中 ∵BD=CD,BH=CH,DH=DH∴△DBH≌△DCH(SSS) 小结:1.这节课学习了什么内容?2.要判定两个三角形全等至少需要多少个条件?3.今天我们学习了判定三角形全等的哪些方法?
如果只满足这些条件中的一部分,那么能保证△ABC ≌△ DEF吗?探索三角形全等的条件1.只给一条边时;3㎝3㎝只给一个条件45?45?2.只给一个角时;3cm45?结论:只有一条边或一个角对应相等的两个三角形不一定全等.①两边;③两角。②一边一角;如果给出两个条件画三角形,
能有哪几种可能的情况?
只给两个条件①如果三角形的两边分别为4cm,6cm 时6cm6cm4cm4cm结论:两条边对应相等的两个三角形不一定全等.①两边;②三角形的一条边为4cm,一个内角为30°时:4cm4cm30?30?结论:一条边一个角对应相等的两个三角形不一定全等.②一边一角;③如果三角形的两个内角分别是30°,45°时结论:两个角对应相等的两个三角形
不一定全等.③两角。结论:只给出一个或两个条件时,都不能保证所画的三角形一定全等。你能得到什么结论吗?①三角;②三边;③两边一角;④两角一边。如果给出三个条件画三角形,
你能说出有哪几种可能的情况?
①三角;--不全等②三边;如果两个三角形的三条边分别对应相等,那么这两个三角形全等吗?探究:你能画出使得AB=3cm 、 BC=4cm AC=5cm的△ABC吗?
你能画出使得AB=3cm 、 BC=5cm 、 AC=6cm的△ABC吗?A/B/C/ABC如果两个三角形的三条边分别对应相等,
那么这两个三角形全等.(S.S.S.)在△ABC与△DEF中AB=DE
AC=DF
BC=EF∴△ABC≌△DEF(SSS)判断两个三角形全等的推理过程,叫做证明三角形全等。如何用符号(数学)语言来表达呢?
例1 如图,AB=CD,AC=BD,△ABC和△DCB是否全等?试说明理由。 例题讲解答: △ABC≌△DCB
理由如下:∵ 在△ABC和△DCB中AB = CDAC = BDBC =CB∴ △ABC≌△DCB(SSS)(公共边)(已知)(已知)归纳:①准备条件:证全等时要用的间接条件要先证好有所需的直接条件;②三角形全等书写三步骤:写出在哪两个三角形中摆出三个条件用大括号括起来写出全等结论证明的书写步骤: A C B D证明:∵D是BC的中点∴BD=CD在△ABD与△ACD中AB=AC(已知)BD=CD(已证)AD=AD(公共边)∴△ABD≌△ACD(SSS)例2 如图, △ABC是一个钢架,AB=AC,AD是连接A与BC中点D的支架,求证: △ABD≌△ACD若要求证:∠B=∠C,你会吗?1 已知:如图,AB=AD,BC=CD,
求证:△ABC≌ △ADCABCDACAC ( ) ≌AB=AD ( )
BC=CD ( )∴ △ABC △ADC(SSS)证明:在△ABC和△ADC中=已知已知 公共边随堂练习: 如图,AB=AC,AE=AD,BD=CE,求证:△AEB ≌ △ ADC。证明:∵BD=CE
∴ BD-ED=CE-ED,即BE=CD。2如图,已知AB=CD,BC=DA。你能说明△ABC与△CDA全等吗?为什么? DBAC解:在△ABC与△CDA中,
∵∴△ABC≌△CDA(SSS)随堂练习:3.已知:如图,AB=AD,BC=CD,
求证:△ABC≌ △ADC4.如图,AB=CD,AC=BD,
求证: △ABC ≌ △DCB 随堂练习:5.如图,C是AB的中点,AD=CE,CD=BE,求证:△ACD≌△CBE随堂练习:6.已知,点A,D,B,F在一条直线上,AD=FB ,AC=FE,BC=DE
证明△ABC ≌△ FDE,ACBDEF随堂练习:拓展思维,才能架起知识的桥梁……7.已知:如图,AB=AC,BD=CD.你能说明∠B=∠C吗?8:如图,AB=AC,BD=CD,BH=CH,图中有几组全等的三角形?它们全等的条件是什么?HDCBA解:有三组。 在△ABH和△ACH中 ∵AB=AC,BH=CH,AH=AH ∴△ABH≌△ACH(SSS);在△ABH和△ACH中∵AB=AC,BD=CD,AD=AD ∴△ABD≌△ACD(SSS);在△ABH和△ACH中 ∵BD=CD,BH=CH,DH=DH∴△DBH≌△DCH(SSS) 小结:1.这节课学习了什么内容?2.要判定两个三角形全等至少需要多少个条件?3.今天我们学习了判定三角形全等的哪些方法?
