11.2三角形全等的条件(二)
文档属性
| 名称 | 11.2三角形全等的条件(二) |  | |
| 格式 | rar | ||
| 文件大小 | 399.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-09-04 16:26:00 | ||
图片预览



文档简介
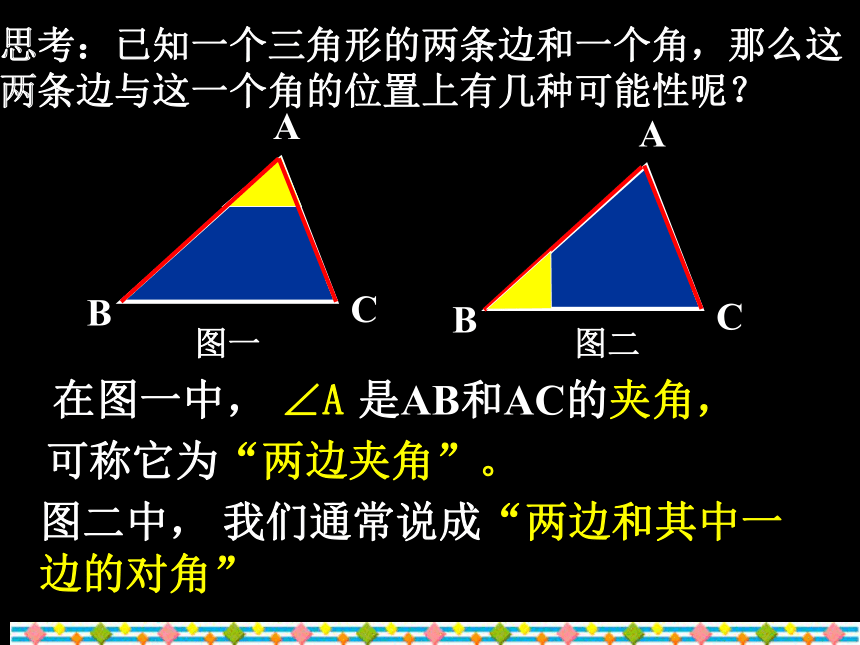
课件22张PPT。11.2三角形全等的条件(二)③三个条件②两个条件①一个条件一边一角两边一角两角一边一角三角三边(SSS)两边两角一边??回顾思考思考:已知一个三角形的两条边和一个角,那么这两条边与这一个角的位置上有几种可能性呢?图一图二在图一中, ∠A是AB和AC的夹角,可称它为“两边夹角”。图二中, 我们通常说成“两边和其中一边的对角”已知△ABC,画一个△A/ B /C / ,使A /B/ =AB ,A/ C/ =AC , ∠A/ = ∠A。结论:两边及夹角对应相等的两个三角形全等(SAS).思考:
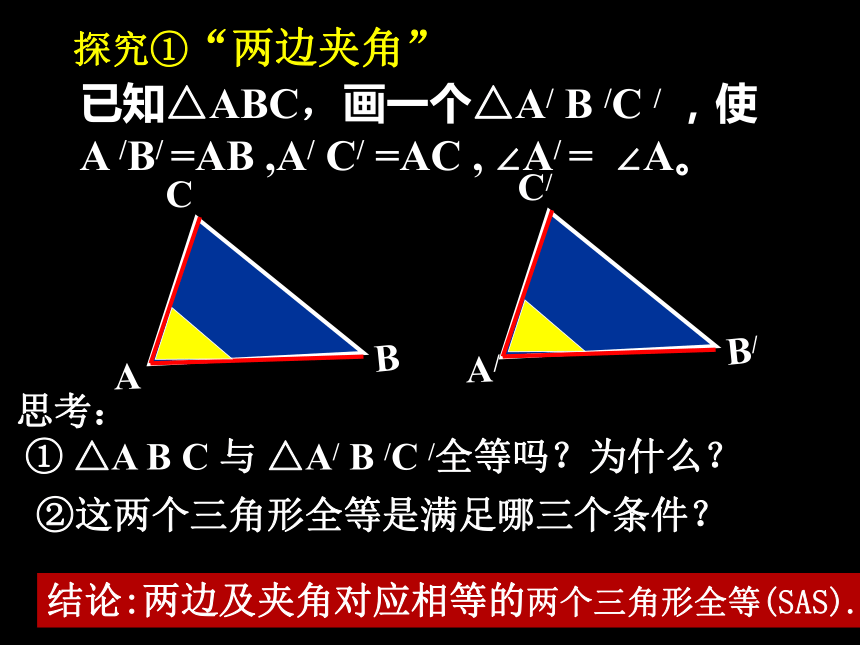
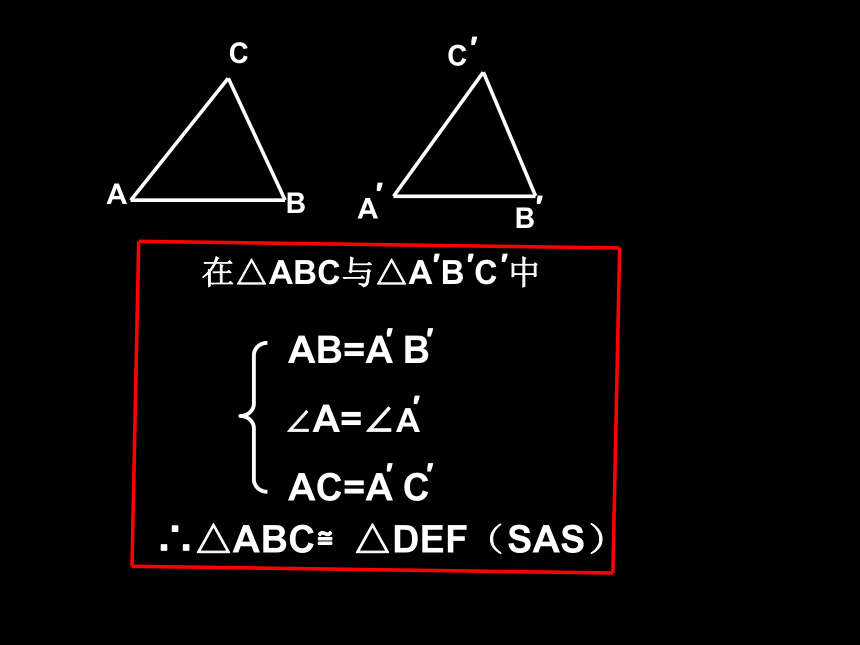
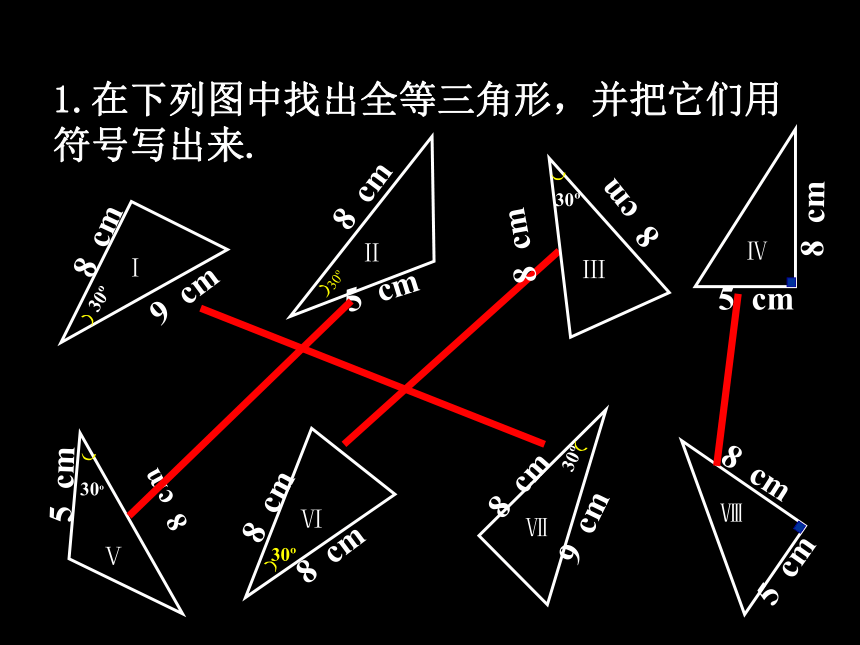
① △A B C 与 △A/ B /C /全等吗?为什么? ②这两个三角形全等是满足哪三个条件?探究①“两边夹角”∴△ABC≌△DEF(SAS)1.在下列图中找出全等三角形,并把它们用
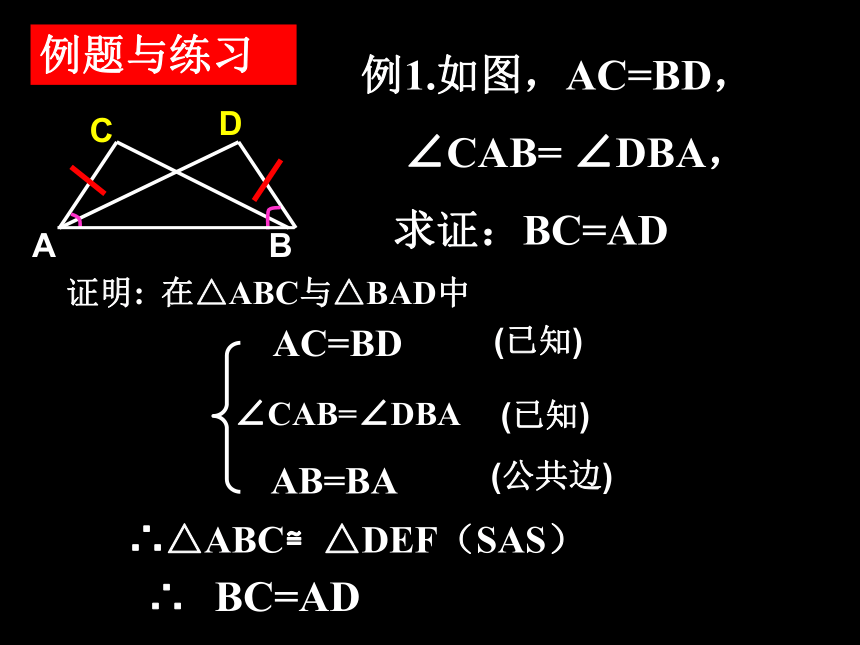
符号写出来.例1.如图,AC=BD,
∠CAB= ∠DBA,
求证:BC=AD证明: 在△ABC与△BAD中 AC=BD
∠CAB=∠DBA
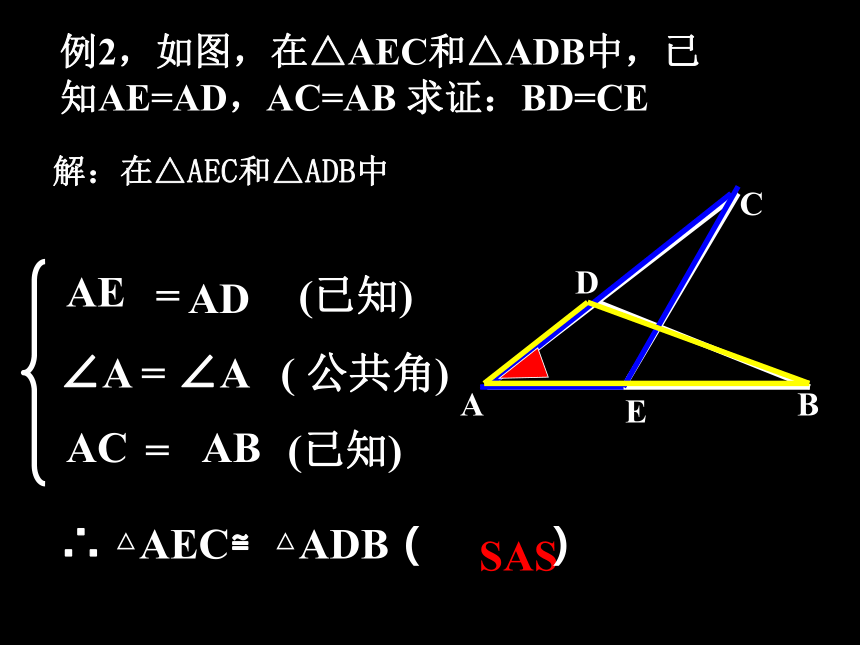
AB=BA∴△ABC≌△DEF(SAS)(已知)(已知)(公共边)∴ BC=AD例题与练习例2,如图,在△AEC和△ADB中,已知AE=AD,AC=AB 求证:BD=CE = (已知)
∠A = ∠A ( 公共角)
= (已知)AEADACABSAS解:在△AEC和△ADB中∴ △AEC≌△ADB( )例3,已知:如图AB=AC,AD=AE,
∠BAC=∠DAE
求证: △ABD≌△ACE例题与练习 1,小明做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,小明不用测量就能知道EH=FH,这是为什么?EFDH根据“SAS” △EDH≌△FDH 所以EH=FH连接EF,那么EF⊥DH吗?说明理由例题与练习结论
线段垂直平分线上的点和这条线段两个端点的距离相等。 已知:如图,直线MN⊥AB,垂足为C,
且AC=CB.点P在MN上.
求证:PA=PB 因铺设电线的需要,要在池塘两侧A、B处各埋设一根电线杆(如图),因无法直接量出A、B两点的距离,现有一足够的米尺。请你设计一种方案,粗略测出A、B两杆之间的距离。 小明的设计方案:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结CD,用米尺测出DE的长,这个长度就等于A,B两点的距离。请你说明理由。40°40°A 以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40° ,情况又怎样?动手画一画,你发现了什么?BCDEF2.5cm3.5cm3.5cm2.5cm结论:两边及其一边所对的角相等,两个三角形不一定全等探究②“两边和其中一边的对角”的两个三角形不一定全等两边及其中一边的对角对应相等①两边及夹角对应相等的两个三角形全等(SAS);② 两边及其中一边的的对角对应相等的两个三角形不一定全等.③ 现在你知道哪些三角形全等的判定方法?SSS, SAS两边及一角对应相等的两个三角形全等吗?
1、今天我们学习哪种方法判定两三角形全等?边角边(SAS) 2、通过这节课,判定三角形全等的条件有哪些?SSS、SAS、注意哦!“边边角”不能判定两个三角形全等
拓展练习1.已知,如图,AB⊥AC,AB=AC,
AD⊥AE,AD=AE。
求证:BE=CD 2.如图,G为正方形ABCD的边CD上一动点(点G与C、D不重合), 以CG为一边向正方形ABCD外作正方形GCEF,连接DE交BG的延长线于H。
求证:① △BCG≌△DCE
② BH⊥DE3.如图,AB=AD,BC=CD,AC、BD交于E,由这些条件可以得出若干结论。请你写出其中三个正确的结论(不要添加字母和辅助线)。(2009年重庆市江津区)如图,在△ABE中,AB=AE,AD=AC,∠BAD=∠EAC, BC、DE交于点O.
求证:△ABC≌△AED;走进中考
① △A B C 与 △A/ B /C /全等吗?为什么? ②这两个三角形全等是满足哪三个条件?探究①“两边夹角”∴△ABC≌△DEF(SAS)1.在下列图中找出全等三角形,并把它们用
符号写出来.例1.如图,AC=BD,
∠CAB= ∠DBA,
求证:BC=AD证明: 在△ABC与△BAD中 AC=BD
∠CAB=∠DBA
AB=BA∴△ABC≌△DEF(SAS)(已知)(已知)(公共边)∴ BC=AD例题与练习例2,如图,在△AEC和△ADB中,已知AE=AD,AC=AB 求证:BD=CE = (已知)
∠A = ∠A ( 公共角)
= (已知)AEADACABSAS解:在△AEC和△ADB中∴ △AEC≌△ADB( )例3,已知:如图AB=AC,AD=AE,
∠BAC=∠DAE
求证: △ABD≌△ACE例题与练习 1,小明做了一个如图所示的风筝,其中∠EDH=∠FDH, ED=FD ,小明不用测量就能知道EH=FH,这是为什么?EFDH根据“SAS” △EDH≌△FDH 所以EH=FH连接EF,那么EF⊥DH吗?说明理由例题与练习结论
线段垂直平分线上的点和这条线段两个端点的距离相等。 已知:如图,直线MN⊥AB,垂足为C,
且AC=CB.点P在MN上.
求证:PA=PB 因铺设电线的需要,要在池塘两侧A、B处各埋设一根电线杆(如图),因无法直接量出A、B两点的距离,现有一足够的米尺。请你设计一种方案,粗略测出A、B两杆之间的距离。 小明的设计方案:先在池塘旁取一个能直接到达A和B处的点C,连结AC并延长至D点,使AC=DC,连结BC并延长至E点,使BC=EC,连结CD,用米尺测出DE的长,这个长度就等于A,B两点的距离。请你说明理由。40°40°A 以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40° ,情况又怎样?动手画一画,你发现了什么?BCDEF2.5cm3.5cm3.5cm2.5cm结论:两边及其一边所对的角相等,两个三角形不一定全等探究②“两边和其中一边的对角”的两个三角形不一定全等两边及其中一边的对角对应相等①两边及夹角对应相等的两个三角形全等(SAS);② 两边及其中一边的的对角对应相等的两个三角形不一定全等.③ 现在你知道哪些三角形全等的判定方法?SSS, SAS两边及一角对应相等的两个三角形全等吗?
1、今天我们学习哪种方法判定两三角形全等?边角边(SAS) 2、通过这节课,判定三角形全等的条件有哪些?SSS、SAS、注意哦!“边边角”不能判定两个三角形全等
拓展练习1.已知,如图,AB⊥AC,AB=AC,
AD⊥AE,AD=AE。
求证:BE=CD 2.如图,G为正方形ABCD的边CD上一动点(点G与C、D不重合), 以CG为一边向正方形ABCD外作正方形GCEF,连接DE交BG的延长线于H。
求证:① △BCG≌△DCE
② BH⊥DE3.如图,AB=AD,BC=CD,AC、BD交于E,由这些条件可以得出若干结论。请你写出其中三个正确的结论(不要添加字母和辅助线)。(2009年重庆市江津区)如图,在△ABE中,AB=AE,AD=AC,∠BAD=∠EAC, BC、DE交于点O.
求证:△ABC≌△AED;走进中考
