11.2.2三角形全等的条件(3)
文档属性
| 名称 | 11.2.2三角形全等的条件(3) |  | |
| 格式 | rar | ||
| 文件大小 | 86.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-09-04 12:17:00 | ||
图片预览




文档简介
课件21张PPT。11.2.2三角形全等的条件
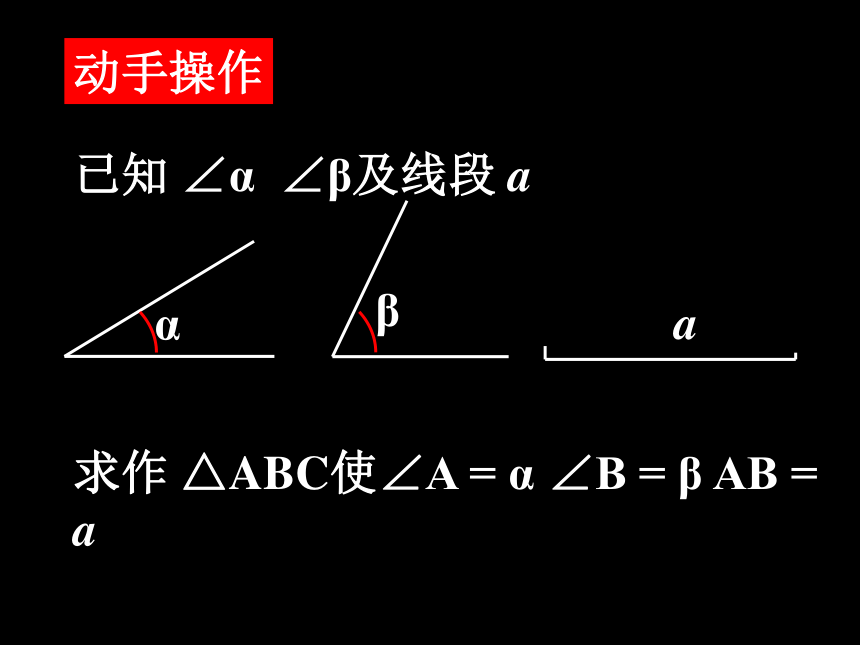
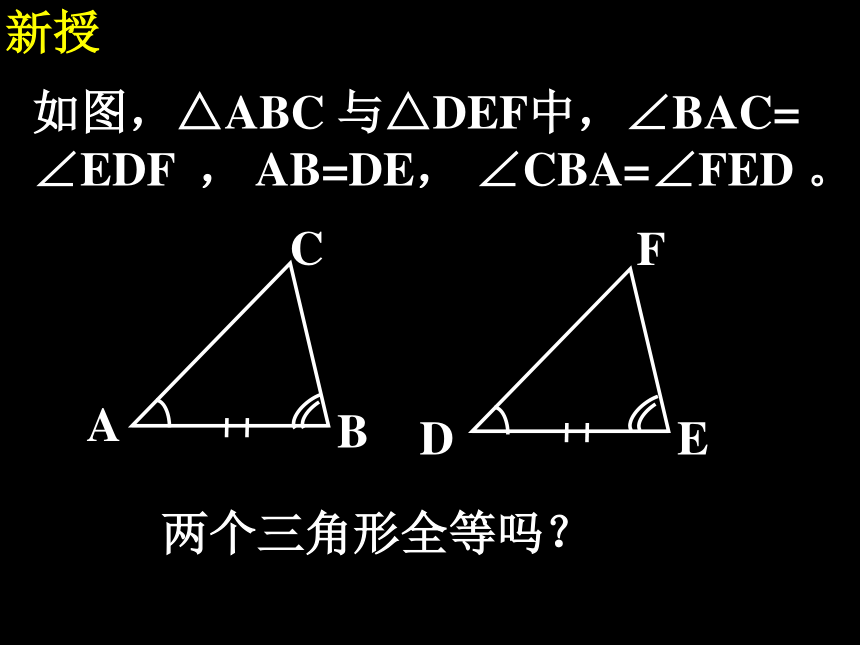
AAS ASA判定两个三角形全等要具备什么条件? 复习 三边对应相等的两个三角形全等。边边边:边角边:有两边和它们夹角对应相等的两个三角形全等。复习与回忆1.我们已学过判定三角形全等的方法有哪些?2.怎样做一个角使它等于已知角?已知 ∠α ∠β及线段 a 求作 △ABC使∠A = α ∠B = β AB = a动手操作新授如图,△ABC 与△DEF中,∠BAC=
∠EDF , AB=DE, ∠CBA=∠FED 。两个三角形全等吗?新授如图,△ABC 与△DEF中,∠BAC=
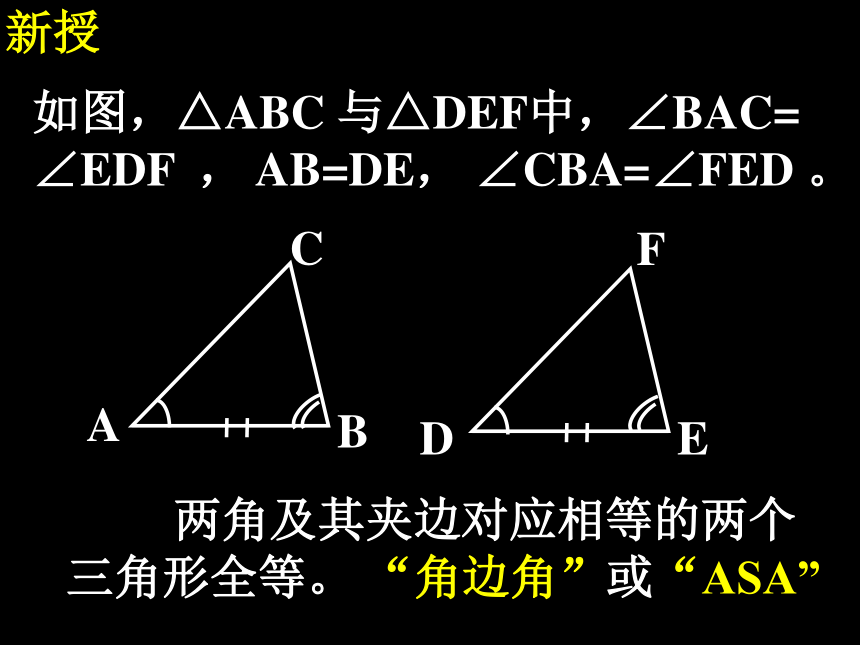
∠EDF , AB=DE, ∠CBA=∠FED 。 两角及其夹边对应相等的两个
三角形全等。 “角边角”或“ASA”新授如图,△ABC 与△DEF中,∠BAC=
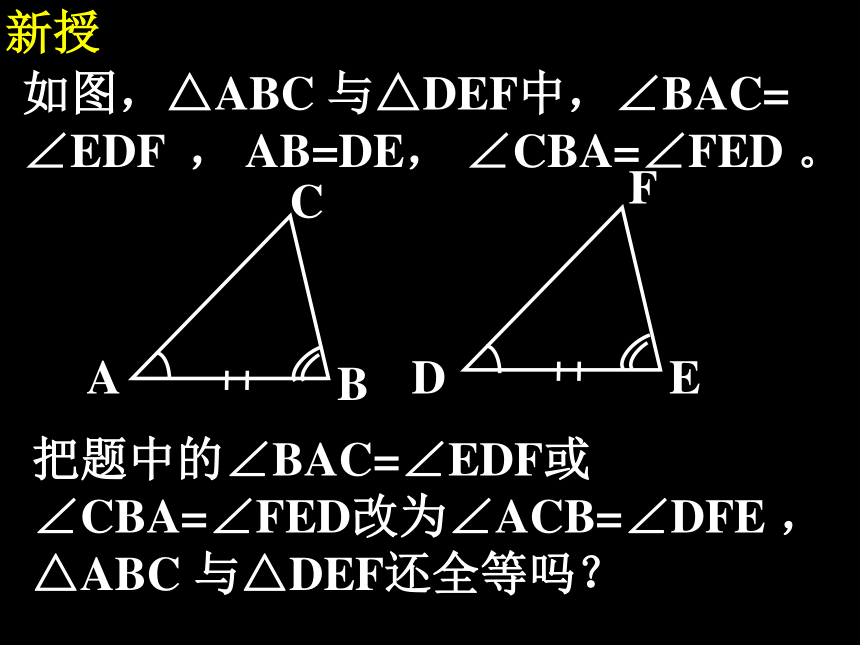
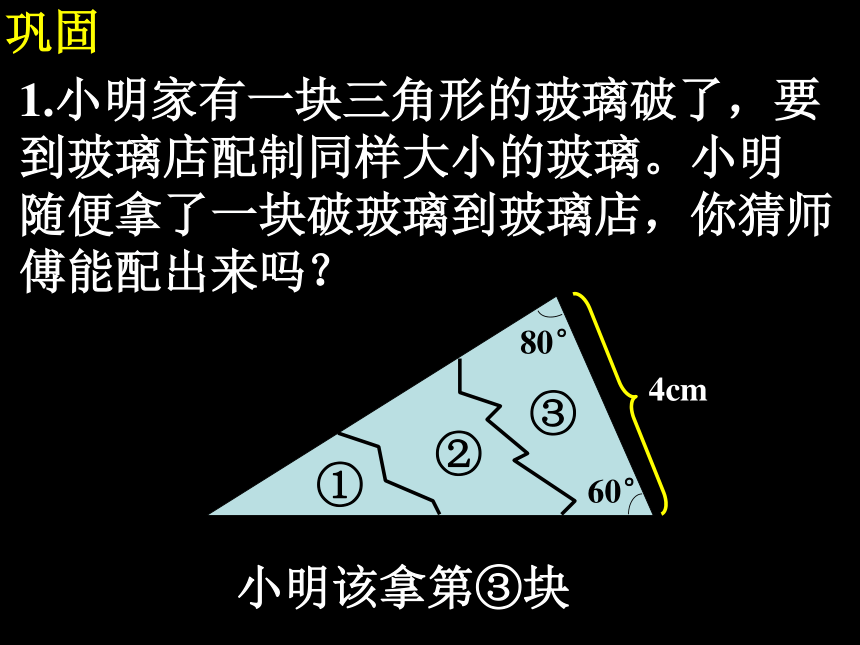
∠EDF , AB=DE, ∠CBA=∠FED 。把题中的∠BAC=∠EDF或 ∠CBA=∠FED改为∠ACB=∠DFE , △ABC 与△DEF还全等吗?小结 1.有两角和它们夹边对应相等的两个三角形全等(简写成“角边角”或“ASA”)。 2.有两角和它们中一角所对的边对应相等的两个三角形全等(简写成“角角边”或“AAS”)。巩固1.小明家有一块三角形的玻璃破了,要
到玻璃店配制同样大小的玻璃。小明
随便拿了一块破玻璃到玻璃店,你猜师
傅能配出来吗?小明该拿第③块巩固2.如图,要测量河两岸相对的两点A、B的距离,可以在AB的垂线BF上取两点C、D,使BC=CD,再定出BF的垂线DE,使A、C、E在同一直线上,这时测得DE的长就是AB的长.为什么?ABCDEF范例例1.如图,点D在AB上,E在AC上,AB=AC,∠B=∠C。
求证:AD=AE。练习1. 如图,∠1=∠2,∠3=∠4
求证:AC=ADACDB练习2已知:如图,∠1=∠2, ∠3=∠4。
求证:AD=BC。例2.如图,△ABC≌△A′B′C′,
AD、A′D′分别是△ABC、△A′B′C′的角平分线。
求证:AD=A′D′。范例练习3如图,△ABC≌△A′B′C′,
AD、A′D′分别是△ABC、△A′B′C′的高。
求证:AD=A′D′练习4.已知:如图, BC∥AD ,AB∥CD 。
求证:△ABC≌△CDA。练习5如图,AC和BD相交于点O,
DC∥AB, DC=AB 。
求证: OA=OC,
OB=OD 。练习6如图,在△ABC中,M是BC的中点,
过点A作射线AMD,并作BE⊥AD于E,
CF⊥AD于F。
求证:ME=MF。练习7已知:如图,已知D、E是△ABC中AB、AC边上的点,且AD=AE,∠1=∠2。
求证:BD=CE。1、(09湖南怀化)如图,已知AB=AD, ∠BAE=∠DAC ,要使 △ABC≌△DAE ,可补充的条件是_______ 走进中考2.(2009年安顺)如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连结BF。
求证:BD=CD;走进中考
AAS ASA判定两个三角形全等要具备什么条件? 复习 三边对应相等的两个三角形全等。边边边:边角边:有两边和它们夹角对应相等的两个三角形全等。复习与回忆1.我们已学过判定三角形全等的方法有哪些?2.怎样做一个角使它等于已知角?已知 ∠α ∠β及线段 a 求作 △ABC使∠A = α ∠B = β AB = a动手操作新授如图,△ABC 与△DEF中,∠BAC=
∠EDF , AB=DE, ∠CBA=∠FED 。两个三角形全等吗?新授如图,△ABC 与△DEF中,∠BAC=
∠EDF , AB=DE, ∠CBA=∠FED 。 两角及其夹边对应相等的两个
三角形全等。 “角边角”或“ASA”新授如图,△ABC 与△DEF中,∠BAC=
∠EDF , AB=DE, ∠CBA=∠FED 。把题中的∠BAC=∠EDF或 ∠CBA=∠FED改为∠ACB=∠DFE , △ABC 与△DEF还全等吗?小结 1.有两角和它们夹边对应相等的两个三角形全等(简写成“角边角”或“ASA”)。 2.有两角和它们中一角所对的边对应相等的两个三角形全等(简写成“角角边”或“AAS”)。巩固1.小明家有一块三角形的玻璃破了,要
到玻璃店配制同样大小的玻璃。小明
随便拿了一块破玻璃到玻璃店,你猜师
傅能配出来吗?小明该拿第③块巩固2.如图,要测量河两岸相对的两点A、B的距离,可以在AB的垂线BF上取两点C、D,使BC=CD,再定出BF的垂线DE,使A、C、E在同一直线上,这时测得DE的长就是AB的长.为什么?ABCDEF范例例1.如图,点D在AB上,E在AC上,AB=AC,∠B=∠C。
求证:AD=AE。练习1. 如图,∠1=∠2,∠3=∠4
求证:AC=ADACDB练习2已知:如图,∠1=∠2, ∠3=∠4。
求证:AD=BC。例2.如图,△ABC≌△A′B′C′,
AD、A′D′分别是△ABC、△A′B′C′的角平分线。
求证:AD=A′D′。范例练习3如图,△ABC≌△A′B′C′,
AD、A′D′分别是△ABC、△A′B′C′的高。
求证:AD=A′D′练习4.已知:如图, BC∥AD ,AB∥CD 。
求证:△ABC≌△CDA。练习5如图,AC和BD相交于点O,
DC∥AB, DC=AB 。
求证: OA=OC,
OB=OD 。练习6如图,在△ABC中,M是BC的中点,
过点A作射线AMD,并作BE⊥AD于E,
CF⊥AD于F。
求证:ME=MF。练习7已知:如图,已知D、E是△ABC中AB、AC边上的点,且AD=AE,∠1=∠2。
求证:BD=CE。1、(09湖南怀化)如图,已知AB=AD, ∠BAE=∠DAC ,要使 △ABC≌△DAE ,可补充的条件是_______ 走进中考2.(2009年安顺)如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连结BF。
求证:BD=CD;走进中考
